Usuwanie składowej stałej
Jak zauważyliśmy już przy analizie na rysunku 8, nasz sygnał z mikrofonu nie oscyluje wokół 0, co oznacza, że znajduje się w nim pewna składowa stała. Jest ona równa napięciu na dzielniku, złożonym z oporników R3 i R4. Istnieje kilka sposobów, aby ją usunąć. Możemy ustalić stałą, którą będziemy odejmować od pomiarów, albo mierzyć napięcie na dzielniku za pomocą drugiego kanału przetwornika. Zastosujemy jednak filtr górnoprzepustowy o nieskończonej odpowiedzi impulsowej: NOI. Często spotyka się także oznaczenie IIR, co pochodzi od angielskiego Infinite Impulse Response [4]. Jego transmitancję wylicza się wzorem:
Taki filtr ma interesującą charakterystykę amplitudową, która wynosi 0 dla składowej stałej, a następnie szybko rośnie. Wyrysujemy ją w notatniku Jupyter. Odpowiedzialny za to kod pokazany jest na listingu 3.
01 α = 31/32
02 H = signal.TransferFunction([1, -1], [1, -α], dt=1e-4)
03 w, mag, phase = H.bode()
04 axi = plt.semilogx(w, mag)
05 plt.xlabel("częstość, rad/s")
06 plt.ylabel("amplituda, dB")
Na początku przyjmujemy współczynnik a równy 31/32. Warto tu zwrócić uwagę, że język Python pozwala nam używać greckich liter jako nazw zmiennych. Można dyskutować, czy jest to dobra praktyka, ale jest to dopuszczalne.
Korzystając z biblioteki Scipy, definiujemy transmitancję H. W formie wektorów podajemy współczynniki wielomianów, składających się na jej licznik oraz mianownik. Ostatni parametr to okres próbkowania. Podajemy tu 100 μs, co odpowiada częstotliwości 10 kHz, z którą pracuje nasz przetwornik. Na końcu generujemy i wyrysowujemy charakterystykę amplitudową (zwaną także charakterystyką Bodego). Uzyskany wykres pokazuje rysunek 9.
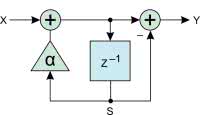
Przed przygotowaniem realizacji filtra w strukturze układu FPGA najpierw pokażmy jego transmitancję w formie graficznej. Na rysunku 10 widzimy jedną z wielu możliwych realizacji. X symbolizuje wejście, a Y wyjście.
Blok z–1 oznacza operację opóźnienia o jeden krok. Możemy łatwo pokazać, że nasz schemat naprawdę odpowiada transmitancji H. Najpierw rozpiszmy wartość w punkcie oznaczonym jako S:
Po przeniesieniu S na jedną stronę równania i uporządkowaniu współczynników otrzymamy:
Teraz możemy rozpisać równanie na wyjście:
Podstawiając wcześniej obliczoną wartość S, otrzymujemy:
Stąd dzieląc przez X, otrzymujemy naszą wyjściową transmitancję:
Przekładając schemat z rysunku 10 na coś, co można zaimplementować w strukturze układu FPGA, otrzymujemy bardziej złożony schemat pokazany na rysunku 11.
Pierwsza rzecz, która rzuca się w oczy, to znacznie większa liczba przerzutników. Zostały one dodane w celu uzyskania wyższej częstotliwości pracy (co prawdopodobnie nie jest potrzebne w naszym, taktowanym z niską częstotliwością 8 MHz projekcie). Zwracam uwagę, że jedynym przerzutnikiem z wejściem ce jest ten oznaczony jako S. Jest on włączany przez sygnał valid. To główna różnica pomiędzy opóźnieniami wynikającymi z logiki projektu (z–1) a tymi „technicznymi”, ułatwiającymi realizację w krzemie. W punkcie S ma zostać zapisana ostatnia „poprawna” (valid) wartość.
Usuwanie składowej stałej realizowane jest w trzech krokach. Pierwszy polega na zatrzaśnięciu wejść. Odpowiadają za to przerzutniki x i valid_d[0].
W drugim kroku przygotowujemy cząstkowe wyniki i zapisujemy je w rejestrach sum_delay i s_delay. Razem z nimi, w valid_d[1] podąża sygnał sterujący. W ostatnim etapie, w przerzutnikach y i valid_d[2] zapisujemy wyjście filtru. Warto zauważyć, że sygnał kontrolny valid niejako płynie przez filtr równolegle z danymi.
Drugi szczegół implantacyjny polega na założeniu, że współczynnik α będzie miał postać 1–2S, gdzie s jest liczbą naturalną. Pozwoli to zastąpić mnożenie za pomocą przesunięcia bitowego i odejmowania. Są to operacje dużo łatwiejsze w realizacji (w FPGA) niż mnożenie.
Musimy jeszcze zastanowić się, ile bitów musimy przeznaczyć na reprezentację stanu. W tym celu przejdźmy do opisu w dziedzinie czasu. Możemy wyrazić wartość w rejestrze s w chwili k+1 jako:
Dla danego (stałego) wejścia x po pewnym czasie stan się ustali. Oznacza to, że wartość sk+1 będzie równa sk. Możemy wtedy zapisać:
I obliczyć wartość stanu ustalonego:
Gdy podstawimy przyjętą przez nas wcześniej wartość współczynnika:
Otrzymamy zależność:
Teraz, jeżeli nasze wejście x ma długość N bitów, to do zapisania stanu s potrzebować będziemy L=N+S bitów.
Mamy już wszystkie niezbędne informacje, aby rozpocząć implementację. Kod napisany w języku SystemVerilog znajdziemy na listingu 4.
10 module dc_r #(
11 parameter N = 8,
12 parameter S = 5
13 ) (
14 StreamBus in,
15 StreamBus out
16 );
17 parameter L = N+S;
18 logic [2:0]valid_d;
19 logic signed [N:0]x;
20 logic signed [L:0]s;
21 logic signed [L:0]sum;
22 logic signed [L:0]s_delay;
23 logic signed [L:0]sum_delay;
24 logic signed [L+1:0]y;
25
26 always_ff @(posedge in.clk or negedge in.rst)
27 if (!in.rst)
28 valid_d <= ‘0;
29 else
30 valid_d <= {valid_d[1:0], in.valid};
31
32 always_ff @(posedge in.clk)
33 x <= {1’d0, in.data};
34
35 assign sum = s - (s >>> S) + x;
36
37 always_ff @(posedge in.clk or negedge in.rst)
38 if (!in.rst)
39 s <= ‘0;
40 else if (valid_d[0])
41 s <= sum[L:0];
42
43 always_ff @(posedge in.clk) begin
44 s_delay <= s;
45 sum_delay <= sum[L:0];
46 end
47
48 always_ff @(posedge in.clk)
49 y <= sum_delay – s_delay;
50
51 assign out.data = y[N-1:0];
52 assign out.valid = valid_d[2];
53 endmodule
Na początku definiujemy dwa znane nam już parametry. N oznacza liczbę bitów przeznaczonych na wejście, a s ustala wartość współczynnika a. Następnie utworzone są dwa interfejsy: wejściowy in i wyjściowy out. Dla uproszczenia nie będziemy implementować sygnału ready. W liniach 17…24 zdefiniowane zostały sygnały wykorzystywane wewnątrz modułu. Te, które przechowują liczby ze znakiem, mają dodatkowy parametr signed.
Pierwszy blok always (linie 26…30) buduje linie opóźniającą dla sygnału valid. W wierszach 32…33 zatrzaskujemy wartość wejściową w rejestrze x.
Dodatkowo, poprzez dołączenie na początek bitu równego 0, dokonujemy konwersji z liczby bez znaku do dodatniej liczby ze znakiem. Z tego powodu, mimo że wchodząca wartość jest zapisana na N bitach, nasz rejestr x musi mieć długość N+1 bitów.
Linia 35 definiuje logikę kombinacyjną, która oblicza wartość pomocniczą sum. Korzystamy tu z operatora arytmetycznego przesunięcia bitowego. W przeciwieństwie do przesunięcia logicznego, zachowuje ono znak. Różnica pomiędzy nimi została pokazana na rysunku 12.
Blok synchroniczny z linii 37…41 realizuje obsługę stanu. Wartość początkowa, ustawiana przy resecie, to 0. Natomiast wartość z sygnału sum jest zatrzaskiwana tylko wtedy, gdy (odpowiednio opóźniony) sygnał valid jest aktywny. Następnie w wierszach 43…46 wykonujemy drugi krok obliczeń. W rejestrach s_delay i sum_delay zatrzaskujemy wartości, których użyjemy do obliczeń. Wynik uzyskujemy w kroku numer trzy (48…49). Zwracam uwagę, że do zapisania różnicy dwóch liczb ze znakiem potrzebujemy rejestru o jeden bit dłuższego niż najdłuższa z wejściowych liczb. Jednak w naszym przypadku z powrotem na wyjście wypisujemy jedynie N najmłodszych bitów.
12 module dc_r_tb;
13 parameter N = 10;
14 logic clk, rst;
15 StreamBus #(.N(N)) in (.clk(clk), .rst(rst));
16 StreamBus #(.N(N)) out (.clk(clk), .rst(rst));
17
18 initial begin
19 clk <= 1’b0;
20 forever #1 clk <= ~clk;
21 end
22
23 initial begin
24 rst <= 1’b0;
25 #4 rst <= 1’b1;
26 end
27
28 initial begin
29 in.valid = 1’b1;
30 for (int i = 0; i < 1000; i++) begin
31 @(posedge clk);
32 in.data = 120*$sin(2*pi*i/100)+480;
33 end
34 $stop;
35 end
36
37 dc_r #(.N(N), .S(5)) dut (
38 .in(in),
39 .out(out));
40 endmodule
Musimy teraz przygotować testbench dla nowego modułu, którego kod pokazuje listing 5. Najpierw definiujemy parametr N, który określa długość szyny danych. Wykorzystamy go dalej do stworzenia interfejsów: wejściowego i wyjściowego. Następnie w dwóch osobnych blokach initial generujemy sygnał zegarowy oraz reset. Linie 28…35 odpowiadają za stworzenie danych. Tworzymy sinusoidę o amplitudzie 120, z przesunięciem 480. Generujemy w pętli 1000 próbek, po czym kończymy symulację. Na samym końcu został umieszczony testowany moduł. Włączamy symulację, wywołując w programie ModelSim komendę:
do dc_r_sim.do
Skrypt jest bardzo podobny do tych, których używaliśmy wcześniej. Warto jednak zwrócić uwagę na nowy przełącznik –decimal. Powoduje on, że dany sygnał jest interpretowany jako liczba ze znakiem i wyświetlany w systemie dziesiętnym.
Wynik symulacji widoczny jest na rysunku 13. Dwa pierwsze wiersze to sygnał zegarowy oraz reset. Następnie widzimy dane wejściowe i ich wersję skonwertowaną na liczbę ze znakiem (oznaczone jako x). Dalej mamy cząstkowy sygnał sum i s. Możemy zaobserwować, jak narastają one w początkowym okresie. Powiązane jest to ze znikaniem składowej stałej w wyjściowym sygnale data, pokazanym w ostatnim wierszu.
Po ustabilizowaniu się sygnału wyjściowego otrzymujemy sygnał oscylujący wokół zera. Na zaprezentowanym rysunku nie są widoczne wszystkie detale, dlatego zachęcam do samodzielnego uruchomienia symulacji.

 Zaloguj
Zaloguj




 Spis treści
Spis treści