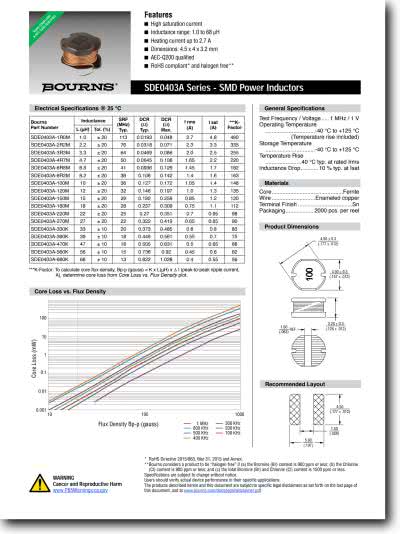
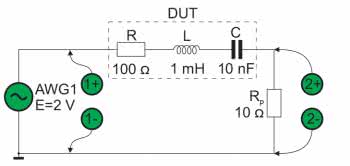
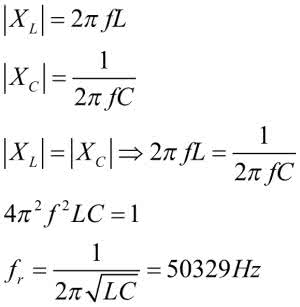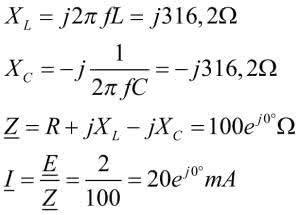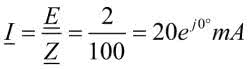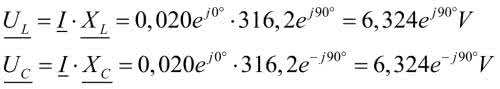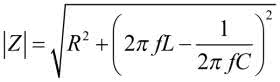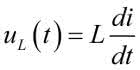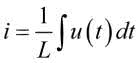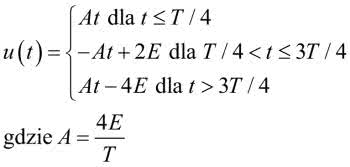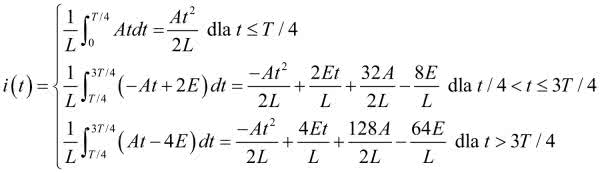Obwód RLC, jak sama nazwa wskazuje, składa się z trzech elementów: rezystora – R, indukcyjności (cewki, dławika itp.) – L i pojemności (kondensatora) – C. W rozważaniach teoretycznych zakładamy zwykle stosowanie elementów idealnych, co oznacza, że w rezystorze nie występują żadne pasożytnicze pojemności montażowe ani indukcyjności np. doprowadzeń, cewka ma zerową rezystancję, a kondensator nie ma żadnych upływności i indukcyjności doprowadzeń. Zakładamy ponadto stałość parametrów w funkcji częstotliwości, temperatury, napięcia pracy, prądu itd. Nie jest to zwykle dobre założenie, o czym prawdopodobnie przekonamy się wkrótce, ale od czegoś trzeba zacząć. W wielu przypadkach takie podejście jest wystarczające, ale prowadząc obliczenia związane z zaawansowanymi projektami wszelkie parametry pasożytnicze powinny być uwzględniane. Ignorowanie ich może prowadzić do problemów z uruchomieniem lub nieprawidłowej pracy urządzenia. Dane te można znaleźć w notach katalogowych cewek, dławików, kondensatorów itp. publikowanych przez producentów elementów. Przykład noty katalogowej dławika firmy Bourns pokazano na rysunku 1.
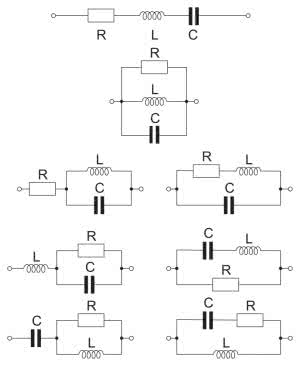
W skład obwodu RLC wchodzą trzy elementy. Występują one w różnych topologiach połączeń. Jest ich 8 (rysunek 2), ale my zajmiemy się tylko jedną z nich, czyli szeregowym połączeniem rezystora, dławika i kondensatora.
Tak jak w poprzednim odcinku mamy do czynienia z elementami reaktancyjnymi, a więc musimy być przygotowani na obliczenia na liczbach zespolonych. I tym razem, jeśli zajdzie taka konieczność, będziemy korzystać z programu WolframAlfa, który jest dostępny on-line.
Rezonans
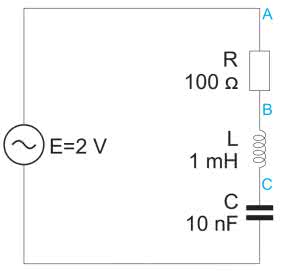
Rozpatrujemy obwód pokazany na rysunku 3. Potraktujmy wszystkie elementy jako idealne. W poprzednim odcinku kompensowaliśmy moc bierną indukcyjną dołączając do obwodu z indukcyjnością kondensator, ponieważ reaktancja pojemnościowa ma przeciwny znak do reaktancji indukcyjnej. Przy zapewnieniu równości tych reaktancji wypadkowa reaktancja przyjmowała wartość zero, tym samym układ nie pobierał mocy biernej. Jest to jednak sytuacja dość specyficzna i warto przyjrzeć się jej bliżej. Należy zauważyć, że z faktu wyzerowania wypadkowej reaktancji nie wynika, że przez poszczególne elementy reaktancyjne nie płynie prąd i nie odkładają się na nich napięcia. Co więcej, w niektórych przypadkach może dochodzić do bardzo groźnych, wręcz katastrofalnych sytuacji. Mamy do czynienia z rezonansem.
Podczas rezonansu energia jest cyklicznie przekazywana z jednego elementu (w naszym przypadku np. kondensatora) do drugiego (cewki), a następnie kierunek przepływu energii zmienia się. Jeśli w danym układzie nie ma żadnych elementów tłumiących, w pobudzonym obwodzie rezonansowym energia będzie rosła do nieskończoności, a skutki tego nie trudno sobie wyobrazić. Mówiąc o obwodach rezonansowych RLC mamy do czynienia z rezonansem elektrycznym, najbardziej spektakularne przypadki tego zjawiska dotyczą jednak rezonansu mechanicznego. 7 listopada 1940 w miejscowości Tacoma w Stanach Zjednoczonych na skutek drgań wywołanych silnym wiatrem w rezonans wpadł most wiszący.
Drgania były na tyle silne (fotografia 1), że konstrukcja ich nie wytrzymała i most uległ zniszczeniu. Zdarzenie zostało dobrze udokumentowane, dostępny jest nawet film: http://bit.ly/2Fu5UED. Nie był to jedyny przypadek wpadnięcia mostu w rezonans. Zagadnienie stało się na tyle poważne, że do dziś w wojskowym regulaminie musztry jest punkt (102) nakazujący dowódcom przeprowadzającym pieszą kolumnę wojskową przez most wydać komendę „Dowolny krok”. Bezładny, nie miarowy krok żołnierzy ma zapobiegać ewentualnemu wprowadzeniu mostu w rezonans. Czy ma to sens czy nie, to już inna sprawa, ale widać, że gdy tworzono regulamin problem traktowano bardzo poważnie.
Wróćmy do naszego układu elektrycznego. Sprawdźmy czego możemy spodziewać się w przypadku, gdy częstotliwość przebiegu zasilającego będzie równa częstotliwości rezonansowej. Wybuchnąć raczej nic nam nie powinno, ale w niekorzystnym przypadku kłopotów możemy się spodziewać. Najpierw, tradycyjnie już wykonamy obliczenia teoretyczne, następnie nasz układ RLC poddamy symulacji w programie LTspice i na koniec sprawdzimy wszystko w działającym układzie z użyciem zestawu Analog Discovery 2.
Obliczenia
Układ, którym się zajmiemy pokazano na rysunku 3. Mamy rezystor 100 Ω, cewkę 1 mH i kondensator 10 nF. Sprawdźmy jaka jest częstotliwość rezonansowa takiego obwodu. Do jej obliczenia korzystamy z faktu, że występuje ona dla równych modułów reaktancji indukcyjnej i pojemnościowej. Rezystancja nie ma żadnego wpływu na częstotliwość rezonansową, zależy od niej natomiast charakterystyka częstotliwościowa obwodu RLC.
Mamy już częstotliwość rezonansową, sprawdźmy jaki prąd popłynie przy zasileniu obwodu przebiegiem sinusoidalnym o napięciu skutecznym 2 V i częstotliwości rezonansowej oraz jakie będą spadki napięć na poszczególnych elementach. Impedancja obwodu jest równa:
W obwodzie popłynie prąd:
Prąd, mimo rezonansu, nie wzrósł do wielkich wartości, gdyż ograniczył go rezystor znajdujący się w obwodzie. Zobaczmy, jakie będą spadki napięć na elementach.
Napięcie skuteczne na rezystorze jest równe napięciu zasilającemu, ale przecież mamy obwód szeregowy, w którym występują jeszcze dwa elementy. Płynie przez nie ten sam prąd co przez rezystor. Musi więc odłożyć się na nich jakieś napięcie. Liczymy:
I rzeczywiście, na cewce i na kondensatorze odkładają się takie same napięcia co do wartości, mają one jednak przeciwne fazy. Co gorsza, napięcia są wielokrotnie wyższe od napięcia zasilającego.
Należy jeszcze zastanowić się nad tym, jak będzie zmieniał się prąd płynący w obwodzie w funkcji częstotliwości. Zależność wydaje się dość oczywista. Dla małych częstotliwości reaktancja kondensatora jest bardzo duża, więc prąd będzie bardzo mały. Podobnie będzie dla dużych częstotliwości, przy czym w tym przypadku prąd będzie ograniczany przez reaktancję cewki. Można więc spodziewać się jakiegoś maksimum, które wypadnie dla częstotliwości rezonansowej. Prąd będzie wówczas zależał tylko od rezystancji. Pamiętajmy jednak, że zgodnie z prawem Ohma rezystancja w wyrażeniu opisującym natężenie prądu występuje w mianowniku, zatem dla zerowej rezystancji prąd w badanym układzie RLC będzie nieskończony.
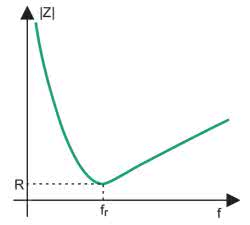
Na koniec rozważań teoretycznych zastanówmy się jeszcze jak będzie wyglądała zależność modułu impedancji od częstotliwości. Analitycznie jest ona opisana następująco:
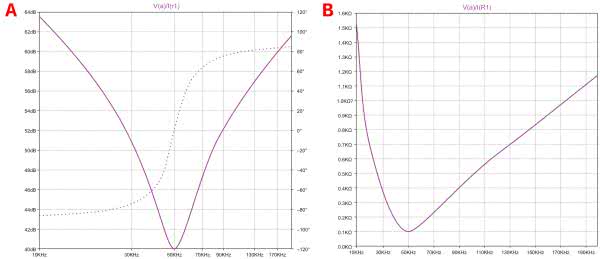
Bez głębszej analizy można sądzić, że zarówno dla częstotliwości dążących do zera, jak i do nieskończoności moduł impedancji będzie również dążył do nieskończoności. Do częstotliwości rezonansowej wykres funkcji modułu impedancji będzie zbliżony do hiperboli, gdyż decydujące znaczenie ma reaktancja pojemnościowa, w której częstotliwość występuje w mianowniku. Powyżej częstotliwości rezonansowej funkcja będzie miała charakter zbliżony do liniowej, gdyż decydować będzie reaktancja indukcyjna, w której częstotliwość występuje w liczniku. Spodziewany przebieg pokazano na rysunku 4.
Symulacja
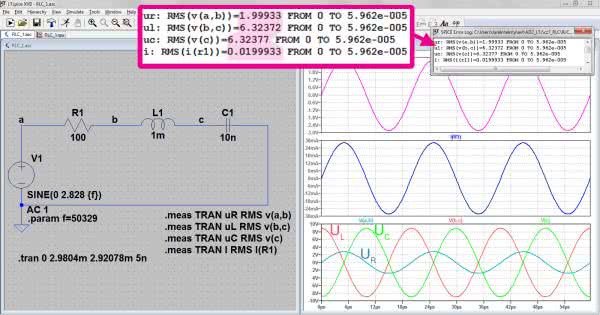
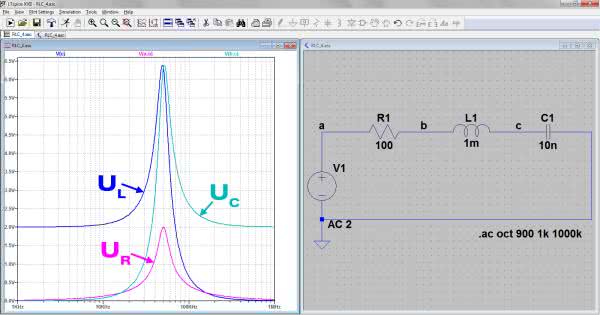
Sprawdźmy po kolei czy nasze obliczenia zostaną potwierdzone w symulacji. W oknie roboczym programu LTspice rysujemy schemat jak na rysunku 5. Zaczynamy od prądu. Z obliczeń wynika, że w stanie rezonansu natężenie prądu jest równe 20 mA i nie ma przesunięcia fazowego między napięciem i prądem. W właściwościach źródła zasilającego wprowadzamy częstotliwość w postaci parametrycznej. Przyjmujemy ponadto amplitudę sygnału równą 2,828 V odpowiadającą napięciu skutecznemu 2 V. Wybieramy przebieg sinusoidalny bez offsetu napięciowego i bez przesunięcia fazowego. Pomiędzy elementy R, L i C wstawiamy etykiety, które ułatwią wykonanie wirtualnych pomiarów spadków napięć. Służące do tego komendy są następujące:
.meas TRAN uR RMS v(a,b)
.meas TRAN uL RMS v(b,c)
.meas TRAN uC RMS v(c)
Wyniki pomiarów przeglądamy w oknie wywołanym poleceniem „View → SPICE Error Log”, są one widoczne na rysunku 5. Symulacja potwierdziła obliczenia. Czytelnicy zapewne już nie dziwią się nietypowym czasom symulacji. Wynikają one z przyjęcia momentów wypadających dokładnie w chwilach początków i końców pełnych okresów przebiegu, przyjmowanych w celu minimalizacji błędów obliczeń wartości skutecznych poszczególnych parametrów. Pokazane na rysunku 5 wyniki wirtualnych pomiarów są zgodne z obliczeniami. Szybką metodą pomiaru pojedynczego parametru jest, jak pamiętamy, naprowadzenie kursora na opis wybranego przebiegu widoczny nad wykresem, naciśnięcie przycisku Ctrl, a następnie lewego przycisku myszki. Pojawia się wówczas ramka zawierająca m.in. wartość średnią i skuteczną.
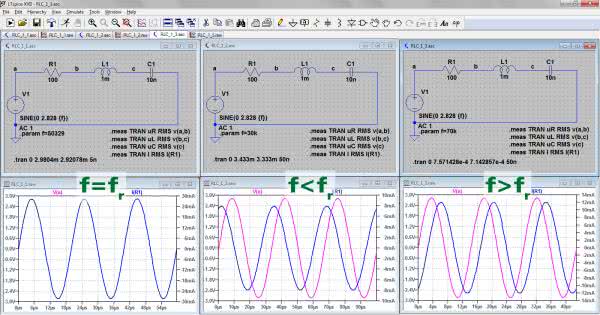
Sprawdźmy jeszcze relacje między napięciem zasilającym i prądem dla częstotliwości niższej i wyższej od częstotliwości rezonansowej.
Na rysunku 6 pokazano kolejno przypadki dla częstotliwości: 50,329 kHz (rezonans), 30 kHz i 70 kHz. Jak widać, w pierwszym przypadku nie występuje przesunięcie fazowe, w drugim prąd wyprzedza napięcie, w trzecim prąd jest opóźniony względem napięcia.
Do wirtualnego pomiaru prądu w funkcji częstotliwości użyjemy funkcji AC ANALISYS. Funkcja ta wyznacza kolejne wartości natężenia prądu dla przemiatanych częstotliwości. Aby jak najdokładniej trafić na częstotliwość rezonansową konieczne jest zastosowanie przemiatania o małym kroku. Dlatego w parametrach tej funkcji wybieramy: Type of sweep=Octave i Number of points per octave=900. Oznacza to, że każda oktawa (2-krotny wzrost częstotliwości) jest podzielona na 900 przedziałów. Pozostaje już tylko zautomatyzowanie pomiaru, do czego używamy funkcji MEASURE. Postępujemy podobnie, jak w pomiarze pasma filtru dolnoprzepustowego w 3. odcinku kursu. Najpierw należy wyznaczyć maksimum dla przebiegu prądowego I=f(f). Zostanie ono zapisane w zmiennej tmp:
MEAS AC tmp MAX mag(I(R1))
Mając ten parametr, w następnej linii można już szukać częstotliwości, dla której obliczone maksimum występuje. Robimy to za pomocą komendy:
.MEAS AC fr TARG mag(I(R1))=tmp
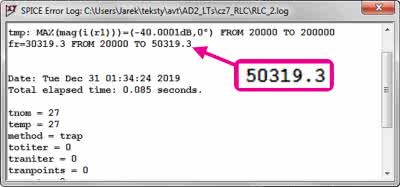
przy czym sam parametr fr nas nie interesuje, za to uwagę należy zwrócić na częstotliwość, przy której pomiar został zakończony. Opcja TARG z występującym po niej argumentem określa warunek zakończenia pomiaru. W naszej symulacji następuje to, gdy prąd osiągnie wartość maksymalną, dlatego odpowiada ona częstotliwości rezonansowej. Dana ta jest wyświetlana w oknie wyników (rysunek 7). Według tego pomiaru częstotliwość rezonansowa badanego obwodu RLC jest równa 50,319 kHz, i jak widać mimo rozpatrywania idealnych elementów różni się od częstotliwości obliczonej (50,329 kHz). Różnica wynika z kroku przemiatania częstotliwości. Po prostu algorytm nie trafił dokładnie w teoretyczną częstotliwość rezonansową.
Pozostało nam jeszcze zweryfikowanie zależności modułu impedancji obwodu RLC od częstotliwości. Do symulacji użyjemy ponownie funkcji AC ANALISYS. Tym razem nie jest konieczna bardzo duża precyzja, więc przyjmujemy 100 punktów na oktawę i pomiar w zakresie od 10 kHz do 200 kHz. Po uruchomieniu symulacji program oczekuje wskazania punktu, do którego będzie odnosił się wykres. Impedancji nie można jednak wskazać bezpośrednio, ale wiemy, że jest ona równa ilorazowi napięcia zasilającego i prądu. Naprowadzamy więc kursor na jakiś punkt znajdujący się w obszarze tworzonego wykresu i klikamy prawym przyciskiem myszy. Z wyświetlonego w tym momencie menu wybieramy Add Traces, a następnie w polu „Expression(s) to add” wpisujemy wyrażenie: V(a)/I(R1). Odpowiada ono impedancji obwodu.
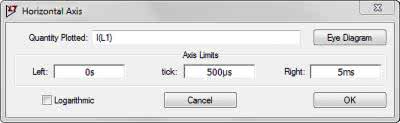
Na ekranie zostanie wyświetlony wykres impedancji w funkcji częstotliwości (rysunek 8a). Nie przypomina on jednak zbyt dokładnie naszych przewidywań pokazanych na rysunku 4. Wynika to z przyjęcia przez symulator logarytmicznej skali częstotliwości i wartości funkcji wyrażanych w decybelach. Na szkicu obie osie są wyskalowane liniowo. Zamieńmy więc skalowanie osi na wykresie LTspice, przy okazji wyłączymy wykres przesunięcia fazowego. W tym celu klikamy prawym przyciskiem myszki w dowolnym miejscu na opisie osi częstotliwości. Na ekranie pojawi się okno dialogowe „Horizontal Axis”, w którym odznaczamy opcję „Logarithmic”. Podobnie klikając na opis prawej osi pionowej wyłączamy wykres fazy naciskając przycisk ekranowy Don’t plot phase. Pozostała jeszcze zmiana osi pionowej. Klikamy prawym przyciskiem myszki na opis lewej osi pionowej i w wyświetlonym oknie dialogowym zmieniamy opcję „Decibel” na „Linear”. Ponadto można wprowadzić wartość 0 w polu „Bottom”. Teraz mamy już pełną zgodność osi z naszym szkicem, i jak widać wykresy są również podobne (rysunek 8b).
Za pomocą symulacji sprawdźmy jeszcze jak będą wyglądały spadki napięć na poszczególnych elementach obwodu w funkcji częstotliwości. Dla niskich częstotliwości o impedancji decyduje kondensator, którego reaktancja jest bardzo duża. To na nim odłoży się prawie całe napięcie zasilające. Wiemy już, że dla częstotliwości rezonansowej napięcie źródła odłoży się w całości na rezystancji, ale na kondensatorze i na cewce wystąpią również napięcia wielokrotnie wyższe od napięcia zasilającego, tyle że będą one miały przeciwne fazy. Dla dużych częstotliwości prawie całe napięcie zasilania odłoży się na cewce, gdyż jej reaktancja rośnie wraz z częstotliwością. Na kondensatorze i na rezystorze spadki napięć będą bliskie zeru.
Uruchamiamy symulację (rysunek 9). We właściwościach źródła zasilającego możemy wybrać opcję „None”. W analizie „AC Analisys”, którą zastosujemy, nie mają znaczenia takie parametry jak amplituda, offset częstotliwość, ważna jest natomiast amplituda sygnału testowego.
Ustawiamy ją w polu „AC Amplitude” na 2 wolty. Takiego napięcia będziemy używać w pomiarach układu rzeczywistego. Wybieramy zakres analizy od 1 kHz do 1 MHz. Na wykresie umieszczamy znanymi metodami przebiegi napięć na rezystorze, cewce i kondensatorze, linearyzujemy ponadto oś pionową (rysunek 9).
Przeprowadzimy jeszcze jedną symulację, której nie rozpatrywaliśmy teoretycznie. Co będzie się działo, gdy nasz szeregowy układ RLC pobudzimy sygnałem prostokątnym? Podświadomie możemy spodziewać się „dziwnych” efektów. Zbadamy przebiegi napięć na elementach obwodu RLC.
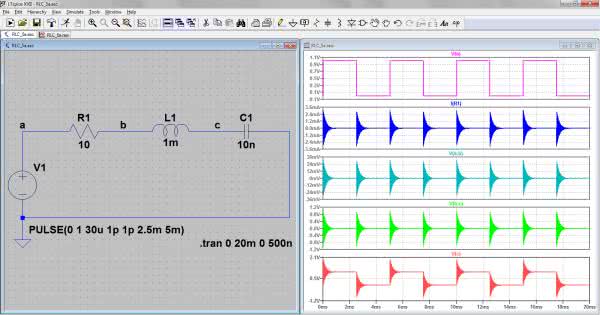
Jako źródło sygnału zastosujemy element biblioteczny „Voltage” z funkcją „PULSE”. We właściwościach wprowadzamy parametry: Vinitial=0, Von=1, Tdelay=30u, Trise=1p, Tfall=1p, Ton=2.5m, Toff=5m. Odpowiadają one przebiegowi prostokątnemu o amplitudzie 1 V (zmiana od 0 do 1 V) i częstotliwości 200 Hz o wypełnieniu 1:1. Należy zauważyć, że czasy narastania i opadania nie są równe 0. Tak jak już było powiedziane, program LTspice nie pozwala na wprowadzanie zerowych wartości niektórych parametrów. Przyjęliśmy więc czasy równe 1 ps, które są na tyle krótkie, że można je ignorować. Dodaliśmy ponadto opóźnienie równe 30 μs, aby wykres obejmował także niewielki przedział czasu przed uruchomieniem źródła zasilającego.
Zmniejszamy rezystor obwodu RLC do 10 Ω. Przyjmujemy czas symulacji 20 ms i maksymalny krok 500 ns. Po rozpoczęciu symulacji klikamy w pole wykresu (w tym momencie jeszcze puste) i za pomocą polecenia „Add Plot Pane” uruchamianego prawym przyciskiem myszki wprowadzamy dodatkowy panel dla wykresu. Czynność tę powtarzamy 4-krotnie, uzyskując 5 paneli dla różnych wykresów. Umieścimy w nich przebiegi na kolejnych elementach obwodu i dodatkowo przebieg napięcia zasilającego i prąd płynący w obwodzie. Na razie panele są puste, wypełniamy je więc od góry. Aby umieścić jakiś przebieg w panelu klikamy w dowolny punkt znajdujący się w jego obrębie lewym przyciskiem myszki – ramka panelu zostanie nieznacznie podświetlona. Następnie wskazujemy interesujący nas punkt lub obiekt na schemacie. W pierwszym panelu umieszczamy napięcie zasilające czyli wskazujemy węzeł „a”. W drugim panelu umieszczamy prąd płynący w obwodzie klikając np. na rezystor r. W trzecim panelu umieszczamy napięcie na rezystorze R1 – V(a,b). Pamiętamy, że robi się to przez przeciągnięcie wirtualnej sondy po kliknięciu na punkt „a” i zwolnieniu przycisku w punkcie „b”. Analogicznie w kolejnych oknach umieszczamy napięcia na cewce i na kondensatorze. Efekt tych czynności pokazano na rysunku 10.
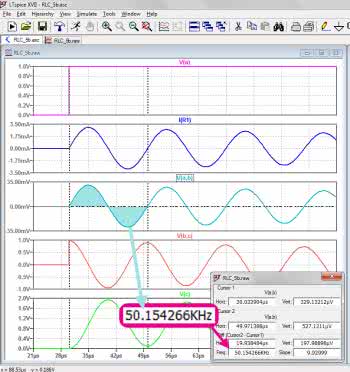
Jak widać z wykresów, tylko napięcie na kondensatorze przypomina napięcie zasilające. Na pozostałych elementach występują jedynie jakieś artefakty, o których na razie niewiele można powiedzieć. Musimy je powiększyć (rozciągnąć skalę czasu w ich pobliżu). W tym celu zakreślamy obszar wokół jednego z zakłóceń, np. pierwszego od lewej strony. Do zaznaczenia używamy lewego przycisku myszki. Efekt powiększenia przedstawiono na rysunku 11. Teraz już wyraźnie widać, że w obwodzie rezonansowym pobudzonym impulsem prostokątnym pojawiły się drgania sinusoidalne. Ich częstotliwość zmierzona za pomocą kursorów jest równa 50,15 kHz. Pomiar z użyciem polecenia MEAS:
.meas TRAN tmp TRIG V(a,b)=0 FALL=1 TARG V(a,b)=0 FALL=2
.meas f PARAM 1/tmp
dał wynik 50218 Hz, a więc bardzo bliski, można powiedzieć, że z dokładnością obliczeniową równy częstotliwości rezonansowej. Jak widać na rysunku 10 drgania mają charakter gasnący. O szybkości ich zaniku decyduje rezystancja.
Zanim przejdziemy do praktycznej weryfikacji pomiarów zastanówmy się jeszcze nad jednym zagadnieniem teoretycznym.
Czy na podstawie przebiegu napięciowego na cewce można określić jej rezystancję?
Tym razem rezygnujemy z kondensatora. Rozpatrujemy połączenie szeregowe rezystora i cewki. Najpierw – proszę nie zaglądać dalej do tekstu – pytanie na intuicję: jaki kształt przyjmie przebieg prądu w szeregowym obwodzie RL przy pobudzeniu go napięciem piłokształtnym, czyli odcinkami liniowym?
Z teorii obwodów wiemy, że zależność między napięciem na cewce i płynącym przez nią prądem jest opisana zależnością:
z czego wynika, że prąd jest równy:
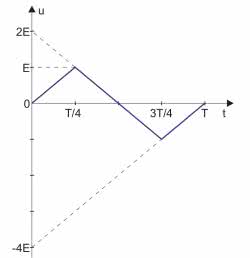
Przebieg z rysunku 12, którego użyjemy do pobudzenia układu jest opisany zależnością:
Wyznaczenie zależności dla prądu wymaga rozwiązania 3 całek, osobno dla każdego z przedziałów. Trzeba pamiętać o takim dobieraniu stałych całkowania, aby zachować ciągłość funkcji opisującej prąd. Spodziewając się, że rozwiązywanie całek może nie być zbyt interesujące dla Czytelników podam końcowe wyniki. Zakładam przy tym, że okres przebiegu jest równy 16 umownych jednostek. Takie założenie uprości obliczenia, a ich celem jest wyznaczenie kształtu przebiegu prądowego, a nie rozwiązanie konkretnego układu. Zakładam ponadto, że w chwili 0 prąd nie płynie. Dla każdego z przedziałów prąd jest opisany poniższymi zależnościami, zachowana jest przy tym jego ciągłość.
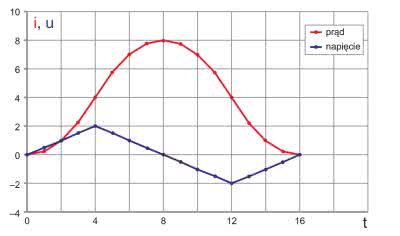
Okazuje się – być może ku pewnemu zdziwieniu – że prąd jest opisany funkcją kwadratową, ma zatem przebieg paraboliczny (rysunek 13).
W związku z tym zaskakującym faktem, wyniki musimy szybko zweryfikować w symulatorze. W edytorze LTspice rysujemy układ pokazany na rysunku 14.
Już na wstępie pojawia się problem: jak wygenerować przebieg piłokształtny? Użyjmy oczywiście standardowego źródła Voltage z zaznaczoną we właściwościach funkcją PWL. Umożliwia ona tworzenie przebiegu składającego się z wielu odcinków przez podanie zbioru par: czas, napięcie. Zbiór ten definiuje kompletny, złożony przebieg, w tym przypadku napięciowy. W definicji występują chwile czasowe, które warto sparametryzować, aby była możliwa np. regulacja częstotliwości. Wprowadzamy więc komendy:
.param f=200Hz
.param dt=1/f
Parametr dt jest równy okresowi przebiegu, do którego będziemy się odnosić wprowadzając poszczególne chwile czasowe. W celu zapętlenia przebiegu w definicji użyjemy ponadto funkcji repeat forever. Kompletny opis źródła prądowego jest następujący:
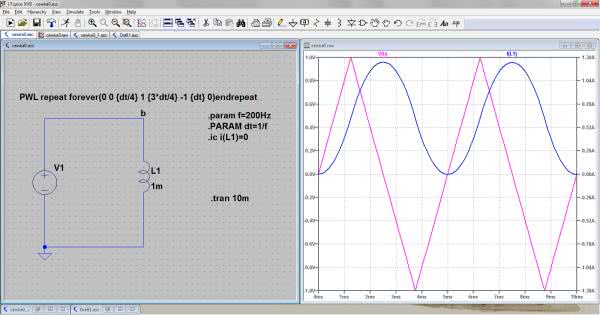
PWL repeat forever(0 0 {dt/4} -1 {3*dt/4} 1 {dt} 0)endrepeat
Jak działa taka funkcja najlepiej przekonać się porównując zapis z przebiegiem przedstawionym na rysunku 14. W symulowanym układzie przyjęliśmy częstotliwość przebiegu równą 200 Hz, wprowadzamy więc parametr Stop time=10m, co odpowiada dwóm okresom. Można ponadto, choć nie jest to w naszym przypadku konieczne, wymusić zerowy prąd w cewce w chwili rozpoczynania symulacji. Służy do tego polecenie:
.ic i(L1)=0
Wynik symulacji pokazano na rysunku 14. Obie osie dopasowano tak, aby zero znalazło się na tym samym poziomie. Jak widać, faktycznie przebieg prądu jest złożony z parabol. Uzyskany wynik może nieco dziwić, gdyż w praktyce rzadko obserwujemy przebiegi prądowe. Gdybyśmy badali napięcie na idealnej cewce za pomocą oscyloskopu, to oczywiście otrzymalibyśmy przebieg piłokształtny generowany przez źródło. Taki przypadek jednak nigdy nie występuje w praktyce, zobaczmy więc, co się stanie gdy zastosujemy elementy rzeczywiste.
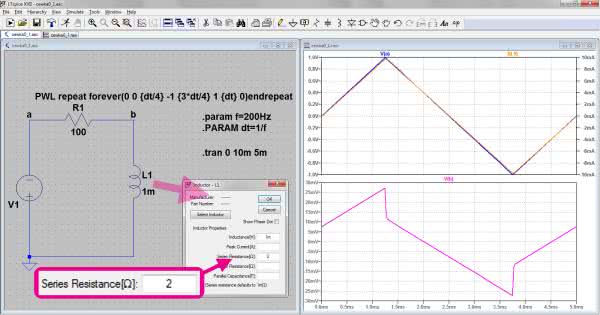
Aby obejrzeć i zmierzyć prąd mając do dyspozycji oscyloskop, dołączamy szeregowo do cewki rezystor. Badając spadek napięcia na nim i znając jego rezystancję możemy określić natężenie prądu płynącego w obwodzie. Zmodyfikowany schemat przedstawiono na rysunku 15. Rezystor R1 będzie wykorzystany później do pomiaru prądu. We właściwościach cewki wprowadzamy parametr Series Resistance=2 oznaczający, że cewka ma własną rezystancję szeregową równą 2 V. Uruchamiamy symulację z parametrami Stop time=10m i Time to start saving data=5m. Oznacza to, że będziemy obserwować tylko drugi cykl przebiegu. Pierwszy pomijamy, aby uniknąć stanu nieustalonego pojawiającego się w chwili startu.
Niebieski przebieg prądu na wykresie z rysunku 15, który w układzie rzeczywistym będzie mierzony oscyloskopem na podstawie spadku napięcia na rezystorze R1 różni się dość znacznie w porównaniu z rysunkiem 14. Na pewno nie jest funkcją kwadratową. Ale coś jest jeszcze nie tak również z napięciem na cewce. To obecność tego rezystora spowodowała tak znaczną linearyzację przebiegu prądowego. Można już nawet uznać, że cewka jest pobudzana prądowo. Z kolei jeśli przyjmiemy liniowe zmiany prądu, to zgodnie ze wzorem (1) napięcie na cewce powinno zmieniać się skokowo i dla piłokształtnego przebiegu prądowego powinno przybierać kształt zbliżony do prostokątnego. Daleki od prostokąta kształt napięcia wynika z względnie małego stosunku rezystancji R1 i rezystancji szeregowej cewki. Łatwo się o tym przekonać zmieniając rezystancję cewki, np. na 0,01 Ω.
Przekształćmy teraz nieznacznie nasz wykres. Zbadajmy zależność napięcia na cewce nie od czasu lecz od płynącego przez nią prądu. W tym celu klikamy prawym przyciskiem myszki na opis osi czasu i w wyświetlonym oknie dialogowym wpisujemy parametr Quantity Plotted=I(L1) (rysunek 16). Wykres przeanalizujemy w Excelu, więc konieczne jest wyeksportowanie danych np. przez plik tekstowy. Klikamy na ramkę okna wykresu, aby go uaktywnić i wykonujemy polecenie: File → Export data as text, następnie podświetlamy parametry V(b) i I(L1), wskazujemy folder i wprowadzamy nazwę pliku. Wszystko zatwierdzamy przyciskiem ekranowym OK. Teraz już można otworzyć Excela i przeciągnąć do niego utworzony plik tekstowy. Może się zdarzyć, że w ostatnim wierszu danych pojawi się błąd. Gdyby tak było, po prostu usuwamy ten wiersz z arkusza.
Do Excela zostały zaimportowane 3 kolumny. Kolumnę zawierającą dane czasowe usuwamy, gdyż nie będzie nam potrzebna. Kolumny powinny być ustawione w kolejności: I(L1), V(b). Jeśli tak nie jest zamieniamy je miejscami. Pozostaje teraz sporządzić wykres na podstawie danych z arkusza. Zaznaczamy je i wybieramy wykres punktowy XY. Po jego utworzeniu naprowadzamy kursor na dowolny punkt wykresu i po naciśnięciu prawego przycisku myszki wybieramy polecenie „Dodaj linię trendu”. Wybieramy wykres liniowy, a w opcjach zaznaczamy pozycję „Wyświetl równanie na ekranie”.
Uzyskujemy wykres jak na rysunku 17a. Linia trendu nie pokryła się dokładnie z prostymi odcinkami wykresu, można więc ograniczyć zakres danych wykresu do fragmentu obejmującego odcinek prostoliniowy. Stały współczynnik przy zmiennej „x” w równaniu regresji jest równy (z dokładnością obliczeniową) ukrytej rezystancji szeregowej cewki. 2 Ω – taką rezystancję szeregową cewki wprowadziliśmy w symulatorze (rysunek 17b).
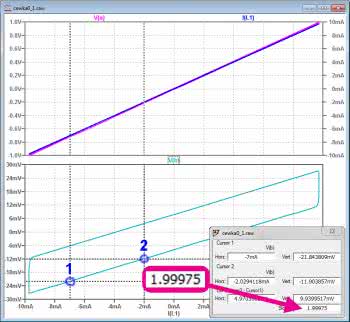
Opisana metoda może być przydatna w pomiarach oscyloskopowych, w programie LTspice do wyznaczenia tego parametru znacznie prościej jest skorzystać z kursorów pomiarowych. Pierwszy kursor ustawiamy w dowolnym punkcie na prostoliniowym odcinku wykresu, drugi na tym samym odcinku lecz w pewnym oddaleniu od pierwszego. Rezystancję odczytujemy w polu Slope parametrów kursorów. Jak widać na rysunku 18 odczytana rezystancja jest równa 1,99975 Ω.
Pomiary
Przyszła kolej na praktyczną weryfikację wszystkich rozważań teoretycznych. W pierwszej kolejności zmierzymy wartości napięć i prądu w szeregowym obwodzie RLC. Do pomiaru prądu użyjemy rezystora obwodu RLC. Dołączymy do niego różnicowo 1. kanał oscyloskopu i tworzymy kanał matematyczny obliczający wyrażenie C1/100 (C1 to wartość odczytana w 1. kanale, a 100 to rezystancja). Uruchamiamy pomiary automatyczne („Measurements”), w których dodajemy pozycje: Defined Measurement → Channel1 → Vertical → AC RMS i analogicznie Max dla kanału matematycznego, któremu można nadać nazwę „prad”. Wybrano parametr Max nie AC RMS, aby uniezależnić się od niedokładności pomiaru występujących przy zmieniającej się częstotliwości sygnału i stałej podstawie czasu oscyloskopu. Zmierzone wartości będą się szybko zmieniać, ich odczyt mógłby być dość trudny, warto więc włączyć uśrednianie wyników. Rozwijamy okno podstawy czasu i w polu Average wybieramy wartość np. 50.
Pierwszą czynnością jest znalezienie rzeczywistej częstotliwości rezonansowej. W dolnej i górnej części suwaka regulacji częstotliwości generatora arbitralnego znajdują się pola, do których należy wpisać minimalną i maksymalną częstotliwość regulacji. Takie rozwiązanie pozwala maksymalnie wykorzystać czułość suwaka. Spodziewając się częstotliwości rezonansowej w okolicach 50 kHz zakres regulacji można zawęzić np. do 48...52 kHz. Uruchamiamy generator i oscyloskop. Regulujemy powoli częstotliwość obserwując wartości zmierzonego natężenia prądu.
Zlokalizowanie maksimum oznacza, że osiągnęliśmy częstotliwość rezonansową. U mnie była ona równa 50,07 kHz, a więc różniła się nieznacznie od obliczonej. Dla tej częstotliwości odczytujemy napięcia na elementach. Kanał 1. jest aktualnie dołączony do rezystora, więc wskazania z niego są równe spadkowi napięcia na rezystancji. W mierzonym układzie napięcie to było równe 1,818 V. Mniejsza wartość od obliczonej wynika z tolerancji elementów oraz ze spadku napięcia na ukrytej rezystancji cewki, która nie była uwzględniana w obliczeniach. Pomiar napięć na cewce i na kondensatorze wymaga przełączenia kanału 1 na te elementy. Po tych zmianach UL=5,892 V, a UC=5,931 V. Choć pomiary różnią się nieznacznie od obliczonych teoretycznie, to jednak mieszczą się w granicach błędu i potwierdzają teorię. Należy jeszcze raz podkreślić występowanie w układzie napięcia wyższego niż zasilające.
Do pomiaru zależności I(f) użyjemy narzędzia Network Analyzer zestawu Analog Discovery 2. Kanał 1. oscyloskopu trzeba dołączyć do generatora, a kanał 2. dołączymy różnicowo do rezystora obwodu RLC. Wybieramy amplitudę sygnału równą 1 V, warto również włączyć podgląd czasowy (Time). I tym razem pomiar z inżynierską dokładnością potwierdził rozważania teoretyczne (rysunek 19).
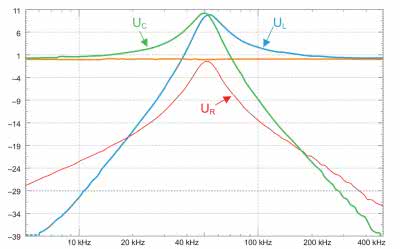
Sprawdzamy jeszcze szybko jak wyglądają spadki napięć na rezystancji, indukcyjności i pojemności w funkcji częstotliwości. Kanał pierwszy pozostaje bez zmian, czyli jest dołączony do generatora, kanał drugi natomiast w kolejnych pomiarach łączymy różnicowo z rezystorem, cewką i kondensatorem. Po każdym pomiarze zapamiętujemy wynik z kanału 2. jako przebieg referencyjny. Można mu również nadać odpowiednią dla pomiaru nazwę. Zebrane wyniki przedstawiono na rysunku 20. Po raz kolejny oddychamy z ulgą – pomiary okazały się zgodne z przewidywaniami.
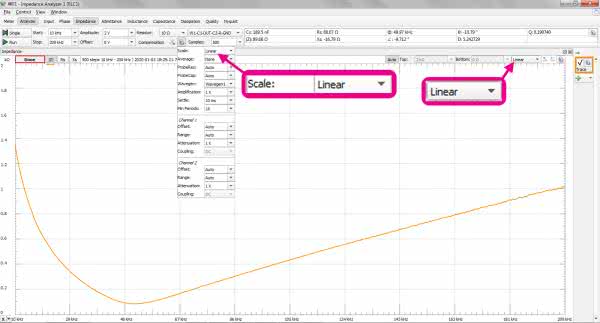
Nieco więcej trudności mogłoby sprawić zmierzenie impedancji za pomocą narzędzia Network Analyzer. Analog Discovery 2 ma jednak specjalny wirtualny przyrząd służący do tego celu. Jest to Impedance. Wymaga on stosowania dodatkowego rezystora pomiarowego Rp dołączanego szeregowo do DUT (Device Under Test). Naszym DUT jest szeregowy obwód RLC, układ pomiarowy wygląda więc tak, jak na rysunku 21.
Przed uruchomieniem pomiaru wprowadzamy parametry: Start=10 kHz, Stop=200 kHz, Amplitude=2 V, Resistor=10 Ω. Schemat pokazany na rysunku 21 odpowiada konfiguracji W1-C1-DUT-C2-R-GND, którą należy wybrać z listy. Pamiętając o tym, że nasze przewidywania pokazane na rysunku 4 były wykonane w liniowo-liniowym układzie współrzędnych, takie skalowanie ustawiamy również w Impedance. Wynik pomiaru pokazano na rysunku 22 i jest on... oczywiście zgodny z teorią.
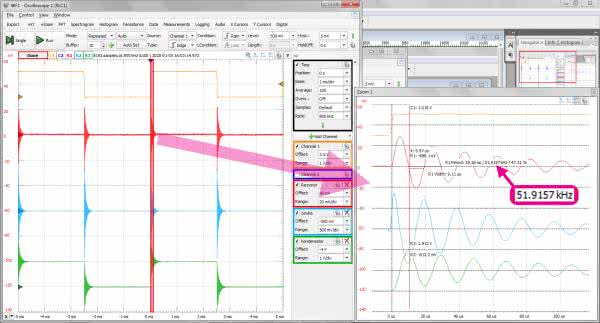
Kolejny pomiar, to badanie odpowiedzi na pobudzenie układu RLC impulsami prostokątnymi. Tak jak w symulacji, ustawiamy w generatorze AWG1 częstotliwość 200 Hz, amplitudę 0,5 V z offsetem 0,5 V (czyli zmianę napięcia od 0 do 1 V). Używając kanału drugiego mierzymy kolejno napięcia na rezystorze, cewce i kondensatorze. Wynik każdego pomiaru zapisujemy jako przebieg referencyjny, co umożliwi nam porównanie trzech przebiegów za pomocą 2-kanałowego generatora.
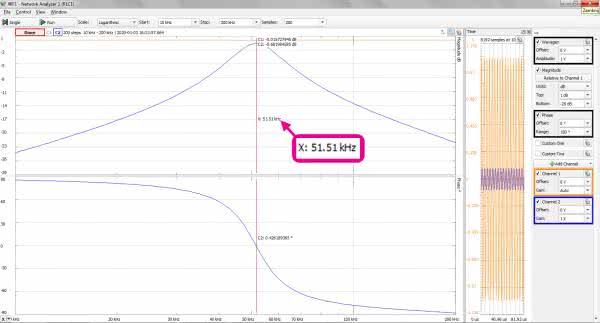
Na podstawie rysunku 23 można wyciągnąć wniosek, że oscylacje obserwowane w chwilach zmiany stanu sygnału wejściowego mają częstotliwość zbliżoną do rezonansowej. Odczytujemy ją w oknie „Zoom” za pomocą kursorów pomiarowych.
Do wykonania pozostał jeszcze pomiar prądu w cewce obwodu RL zasilanego napięciem piłokształtnym. Pamiętamy, że na jego podstawie można określić rezystancję wewnętrzną cewki. W symulacji to się udało, ciekawe czy pomiar również da nam poprawny wynik?
Szeregowo z cewką łączymy rezystor 100 Ω. W generatorze AWG1 ustawiamy napięcie piłokształtne o amplitudzie 1 V i częstotliwości 200 Hz.
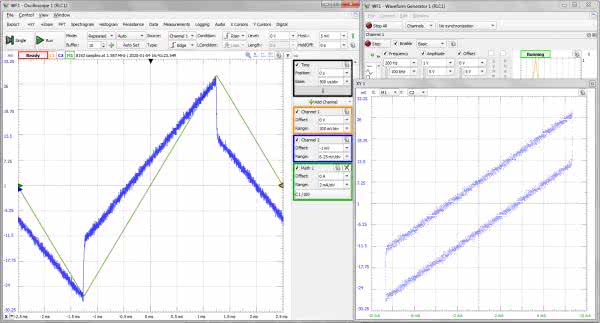
Kanał 1. łączymy różnicowo z rezystorem i definiujemy kanał matematyczny, który oblicza zależność C1/100. Już chyba nie trzeba tłumaczyć, że będzie on mierzył natężenie prądu. Kanał 2. dołączamy do cewki. Po uruchomieniu generatora i oscyloskopu na ekranie ukazuje się oscylogram przypominający ten z symulacji, jest więc nadzieja na poprawny wynik (rysunek 24).
Dokładamy więc wykres XY, dla którego oś X wiążemy z kanałem M1 (prąd), a oś Y z kanałem C2 (napięcie na cewce). Możemy już wyeksportować dane: File → Export → Source=XY1, Data najwygodniej przez clipboard (opcja Copy to Clipboard). Otwieramy pusty arkusz Excela i kopiujemy do niego zawartość pamięci podręcznej.
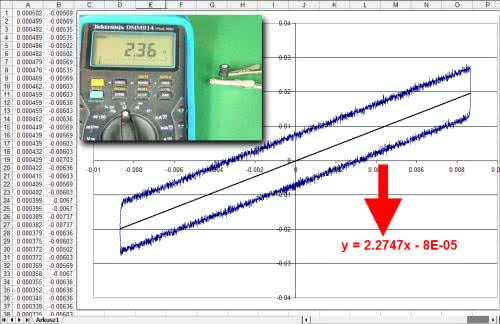
Następnie tworzymy wykres punktowy, do którego dodajemy linię trendu, dokładnie tak samo, jak w symulacji (rysunek 25). Z pomiaru wynika, że rezystancja wewnętrzna cewki jest równa 2,2747 Ω. Aby mieć spokojne sumienie wynik weryfikujemy mierząc jeszcze raz rezystancję cewki multimetrem. Wynik: 2,36 Ω, od którego należy odliczyć rezystancję kabli. Całkiem nieźle. W tym odcinku to już wszystko, a w kolejnym zrobimy... radionamiernik RAF-u.
Jarosław Doliński, EP

 Zaloguj
Zaloguj