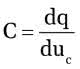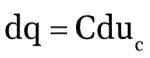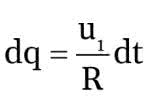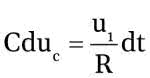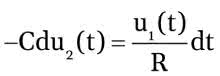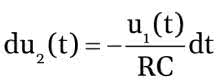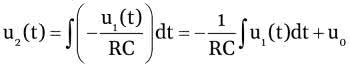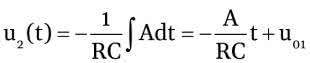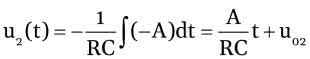O przetwornikach delta-sigma czy sigma-delta słyszał na pewno każdy elektronik, a wielu z nich nawet zastosowało je w swoich projektach. Dobierając przetworniki zwykle rozpatrujemy najpierw ich parametry, takie jak maksymalna częstotliwość próbkowania, rozdzielczość, dynamika, szumy, liniowość itp., nie zastanawiamy się natomiast nad zasadą działania. Postępowanie takie jest poniekąd słuszne, bo jeśli dany przetwornik spełnia nasze wymagania, to informacja o tym, na jakiej zasadzie działa jest w sumie nieistotna. Trudno, abyśmy analizowali budowę wewnętrzną każdego elementu używanego do budowy urządzeń. Owszem, taka wiedza jest przydatna, gdyż na podstawie tylko samych danych katalogowych czasami nie jest możliwe określenie np. ograniczeń danego podzespołu wynikających z jego konstrukcji i zasady działania. W dalszej części przyjrzymy się bliżej bardzo popularnemu przetwornikowi analogowo-cyfrowemu typu sigma-delta.
Próbkowanie i kwantyzacja
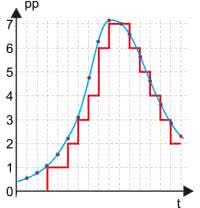
Przetwarzanie analogowo-cyfrowe to proces polegający na zamianie analogowego sygnału wejściowego, np. napięcia, na dyskretne wartości cyfrowe. Dyskretne, czyli takie, które stanowią skończony, policzalny zbiór wartości. Dyskretyzacji podlega zarówno czas, jak i poziom sygnału. W literaturze opisującej zagadnienia związane z przetwarzaniem sygnałów spotykamy się z dwoma charakterystycznymi dla tego procesu pojęciami: próbkowaniem i kwantyzacją. Próbkowanie to pobieranie wartości chwilowych sygnału w określonych, najczęściej stałych odstępach czasu. W wyniku kwantyzacji każdej próbce nadawana jest konkretna, jednoznaczna wartość liczbowa opisująca chwilową wartość sygnału w momencie próbkowania (rysunek 1). Liczba takich wartości jest zależna od rozdzielczości przetwornika. Jest to zwykle wielokrotność liczby 2.
Spotykamy się często z określeniem, że jakiś przetwornik jest n-bitowy. Oznacza że uzyskiwane z niego wartości przybierają 2n poziomów. Przykładowo, w 3-bitowym przetworniku uzyskujemy 8 poziomów (od 0 do 7), tak jak to pokazano na rysunku 1. Jest to dość oczywisty i naturalny opis procesu próbkowania. Osobną kwestią pozostaje natomiast metoda przypisywania wartości liczbowej każdej próbce, ale nie będziemy się tu zajmować tym zagadnieniem. Przyjmujemy zatem, że mamy na przykład jakiś n-bitowy rejestr z wyjściami równoległymi, do którego są wpisywane kolejne wartości próbek zbieranych w takt specjalnego zegara. W ustalonych odstępach czasu uzyskujemy więc pełną informację o wartości sygnału w chwili próbkowania. Cyfrowa postać takich danych nadaje się świetnie na przykład do zapisywania ich w pamięci, a także do niemal dowolnej obróbki przez jakiś procesor. Powstaje jednak pytanie czy konieczne jest przekazywanie pełnej informacji o wartości każdej próbki? Można wyobrazić sobie na przykład metodę, w której przekazywana jest jedynie różnica wartości kolejnych próbek. Taka koncepcja mogłaby teoretycznie uprościć przesyłanie danych z przetwornika do układu nadrzędnego, np. do procesora. Czy jest to dobry tok myślenia, przeanalizujemy w dalszej części artykułu.
Sigma-delta czy delta-sigma?
Pomysł przesyłania różnic pomiędzy kolejnymi próbkami zamiast pełnych próbek powstał jeszcze w latach 40. XX wieku, ale praktyczne zastosowania można datować dopiero w okolicach początku lat 50. XX wieku. Prowadzono wówczas prace nad modulatorami PCM (Pulse Code Modulation) i technikami transmisji danych. Teoria związana z tą tematyką w zasadzie dopiero powstawała. Pojawiały się nieliczne publikacje, zgłaszano pierwsze patenty. Szczególne znaczenie miały dwie prace opublikowane w latach 1962 i 1963, w których opisano zagadnienia związane z kształtowaniem szumu i nadpróbkowaniem zastosowanym w przetworniku 1-bitowym. Autorzy użyli po raz pierwszy terminu „delta-sigma”. W kolejnych publikacjach był on konsekwentnie powtarzany, aż do lat 70. XX wieku. W tym czasie inżynierowie AT&T nie wiedzieć czemu zaczęli stosować nazwę „sigma-delta”. Oba terminy są od tego czasu używane zamiennie. Każdy z nich jest poprawny. Oba dotyczą też tego samego urządzenia. Specjaliści uznają jednak, że nazwa „sigma-delta” jest z jakichś powodów bardziej poprawna.
Integrator
Zasada działania przetwornika sigma-delta jest w gruncie rzeczy bardzo prosta, lecz do jej poznania zniechęcają spotykane w publikacjach schematy blokowe i rozważania o szumach kwantyzacji. Wielu czytelników kończy lekturę artykułu na samym leadzie widząc tajemnicze bloki z symbolami całek, a także liczne wzorki z logarytmami i tajemniczymi liczbami, które nie wiadomo skąd się biorą,. Nie unikniemy tych elementów i w niniejszym opracowaniu. Zrozumienie zasady działania przetwornika sigma-delta nie wymaga jednak dogłębnej analizy zagadnień matematycznych, stosowne fragmenty można spokojnie pominąć.
I to jest właśnie ten moment, w którym muszą pojawić się informacje znacznie ułatwiające zrozumienie dalszej zżęci artykułu, ale sięgające po aparat matematyczny. Jednym z kilku bloków funkcjonalnych wchodzących w skład przetwornika sigma-delta jest integrator, czyli nieszczęsny układ całkujący widoczny na każdym schemacie przetwornika sigma-delta.
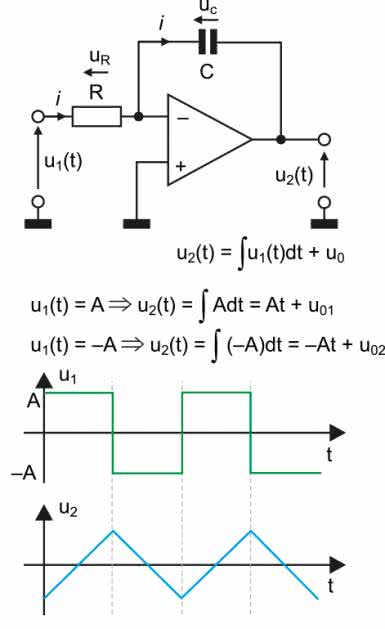
Podstawowy schemat integratora został pokazany na rysunku 2. Jak widać, składa się on ze wzmacniacza operacyjnego pracującego w konfiguracji z wejściem odwracającym. Zamiast spotykanego zwykle rezystora sprzężenia zwrotnego został dołączony kondensator C. Przeanalizujmy działanie tego układu przy założeniu, że mamy do czynienia z idealnym wzmacniaczem operacyjnym. Z takiego założenia wynika, że wzmacniacz ma nieskończenie wielkie wzmocnienie, do wejść U– i U+ nie wpływają żadne prądy, napięcie między wyjściami U– i U+ jest równe zero. Z faktu, że do wejść nie wpływają żadne prądy wynika, że przez rezystor R i kondensator C płynie jeden prąd i. Skoro wejście U+ jest dołączone do masy, to potencjał wejścia U– jest również równy zero, można więc napisać, że prąd i=u1/R. Wiemy też, że pojemność elektryczna jest definiowana jako stosunek zmian ładunku do zmian napięcia:
Zmiany ładunku są więc równe:
Ale zmiany ładunku w czasie definiują też prąd. Mamy więc:
czyli
Na tej podstawie możemy napisać:
Zauważmy, że napięcie na kondensatorze uC jest (zgodnie ze strzałkowaniem przyjętym na schemacie) równe: uc=–u2. Napięcia u1, u2 i uc są zmienne w czasie, dla podkreślenia tego faktu zastosujemy oznaczenia: u1(t), u2(t) i uc(t). Mamy więc:
czyli:
Po obustronnym scałkowaniu równania otrzymujemy:
Jak widać, rzeczywiście w przedstawionym układzie napięcie wyjściowe integratora jest równe całce z napięcia wejściowego. Znak minus oznacza, ze zostanie zmieniona faza sygnału wyjściowego, czynnik u0 ustala natomiast warunki początkowe.
Zobaczmy teraz, co będzie się działo, jeśli do wejścia zostanie doprowadzony symetryczny przebieg prostokątny o amplitudzie A. Możemy przyjąć, że w przedziale od 0 do T/2 reprezentuje on funkcję stałą u1(t)=A, a w przedziale od T/2 do T u1(t)=–A
Napięcie wyjściowe dla pierwszego przedziału jest więc równe:
dla drugiego przedziału natomiast:
Z powyższych wyrażeń wynika, że przykładając napięcie prostokątne do wejścia integratora uzyskamy na jego wyjściu przebieg liniowo opadający (dla t z przedziału od 0 do T/2) i liniowo narastający (dla t z przedziału od T/2 do T), jest to więc przebieg trójkątny. Wynika z tego ważny wniosek: dodatnie stałe napięcie wejściowe integratora powoduje generowanie przebiegu liniowo opadającego, zaś ujemne stałe napięcie wejściowe powoduje generowanie przebiegu liniowo narastającego.
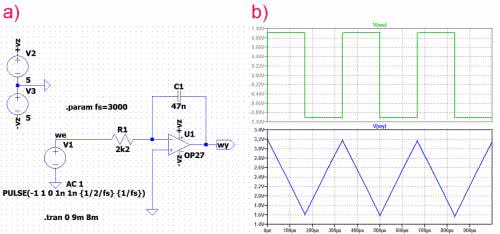
Sprawdźmy to w programie LTspice. Na rysunku 3a został pokazany schemat integratora utworzony w symulatorze. Zastosowano w nim układ operacyjny OP27. Widoczne na rysunku 3b wyniki potwierdzają wcześniejsze rozważania teoretyczne. Dodatniemu napięciu wejściowemu towarzyszy opadające napięcie wyjściowe, zaś ujemne napięcie wejściowe powoduje generowanie napięcia narastającego na wyjściu. Do symulacji został przyjęty czas symulacji równy 1 ms, przy czym uwzględniono 8 milisekundowy czas przeznaczony na eliminację ewentualnych stanów nieustalonych. Wydaje się, że wszystko jest w porządku, ale nieco niepokojący jest stosunkowo wysoki offset przebiegu wyjściowego. Jego wartość średnia powinna być równa teoretycznie zero, a jest równa 2,39 V. Zobaczmy więc co się stanie, jeśli czas symulacji wydłużymy drastycznie np. do 70 sekund. Wynik takiej symulacji jest widoczny na rysunku 4.
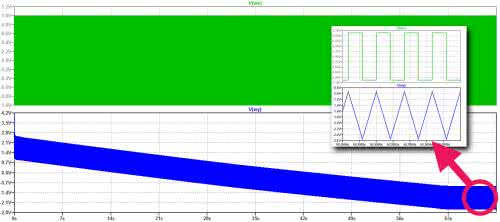
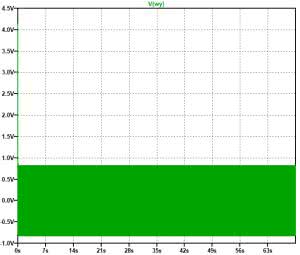
Okazuje się, że na skutek niedoskonałości elementów uwzględnionych nawet w modelu układu OP27, integrator nie pracuje stabilnie. W tym przypadku średnie napięcie wyjściowe ulega stopniowemu zmniejszaniu. Aby zabezpieczyć układ przed takimi zjawiskami najczęściej dodaje się równoległy do kondensatora rezystor o dużej rezystancji, tak aby nie wpływała na warunki pracy integratora, a kompensowała jedynie jego niedoskonałości. Zwykle wystarczający jest rezystor rzędu kilkuset kiloomów. Sprawdźmy, czy rezystor 300 kΩ okaże się wystarczający? Wynik symulacji dla poprawionej konstrukcji pokazano na rysunku 5.
Modulator delta – zasada działania
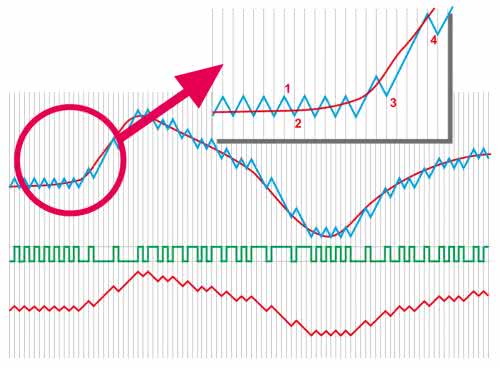
Powróćmy do koncepcji zapisywania w kolejnych próbkach nie pełnej wartości sygnału w chwili próbkowania, a jedynie różnicy w stosunku do poprzedniej próbki. Wymaga to zastosowania jakiegoś mechanizmu na bieżąco śledzącego sygnał wejściowy, co najmniej w zakresie dwóch próbek – bieżącej i poprzedniej. Układ zrealizowany według tej koncepcji jest nazywany modulatorem „delta”. Śledzenie przebiegu wejściowego polega na wytworzeniu porównywanego z nim przebiegu piłokształtnego (rysunek 6). Jeśli w momentach wyznaczonych zegarem taktującym przebieg piłokształtny ma wyższy poziom niż przebieg wejściowy następuje przełączenie kierunku zmian. Na przykład w chwili „1” (rysunek 6) narastający sygnał śledzący ma wartość większą niż sygnał wejściowy, zostaje zatem przełączony kierunek zmian.
Okazuje się, że już w kolejnej próbce malejący sygnał ma wartość mniejszą niż sygnał wejściowy, a więc ponownie następuje zmiana kierunku, Jak można wywnioskować na podstawie tego przykładu, sygnał wyjściowy modulatora dla stałego sygnału wejściowego nigdy nie będzie stały, lecz będzie „myszkować” wokół tej wartości.
W punkcie „3” z rysunku 6 ściganie napięcia wejściowego trwa aż 4 takty zegara próbkującego (do chwili „4”). Do przełączania kierunku zmian napięcia śledzącego zastosowano przerzutnik „D”. Do jego wejścia zegarowego jest doprowadzony sygnał z generatora taktującego decydującego o częstotliwości próbkowania. Z kolei do wejścia D jest doprowadzony wynik porównania uzyskany na przykład z komparatora. Należy zauważyć, że przerzutnik generuje strumień danych cyfrowych niosący informację o analogowym sygnale wejściowym. Układ może więc pełnić funkcję przetwornika analogowo-cyfrowego. Jeśli do wyjścia przerzutnika zostałby dołączony filtr dolnoprzepustowy, na jego wyjściu uzyskalibyśmy odtworzony sygnał wejściowy.
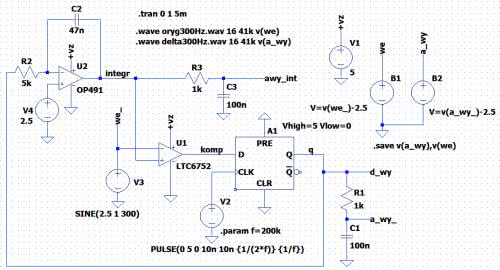
Sprawdźmy działanie takiego układu w symulatorze LTspice (rysunek 7). Sygnał wejściowy – sinusoida o częstotliwości 300 Hz, amplitudzie 1 V ze składową stałą 2,5 V jest tworzony przez źródło napięciowe V3. Sygnał ten jest porównywany przez komparator U1 (LTC6752) z piłokształtnym sygnałem integratora zbudowanego na układzie U2 (OP491). Wyjście komparatora przyjmuje stan wysoki lub niski, zależnie od wyniku porównania. Stan ten jest zatrzaskiwany w przerzutniku „D” (A1). Wyjście przerzutnika jest dołączone do wejścia integratora. Jeśli na tym wejściu występuje stan niski, integrator generuje liniowy przebieg narastający. Zamienia się on w przebieg opadający, gdy na wejściu jest stan wysoki. Jako przerzutnik został zastosowany standardowy element biblioteczny LTspice’a dflop pobrany z sekcji „Digital”. Z uwagi na zastosowane zasilanie +5 V konieczne jest dopisanie w jego właściwościach linii:
Są w niej zdefiniowane poziomy logiczne dla tego elementu. Wejście zegarowe jest sterowane przebiegiem impulsowym generowanym przez źródło V2. Przebieg ten jest zdefiniowany formułą:
Jak widać, zastosowano tu parametryczne określenie częstotliwości próbkowania, którą łatwo można zmienić komendą:
Domyślnie przyjęto 200 kHz.
Warto by było jeszcze ocenić jakość przetwarzania. Najlepszy będzie odsłuch sygnału oryginalnego i przetworzonego. W tym celu zostały użyte komendy:
.wave delta300Hz.wav 16 41k v(a_wy)
Powodują one wygenerowanie dwóch plików dźwiękowych o nazwach oryg300Hz.wav (oryginał) i delta300Hz.wav (sygnał wyjściowy modulatora). Po zakończonej symulacji można je odsłuchać w dowolnym odtwarzaczu plików .wav. Konieczny jest jednak do tego pewien zabieg polegający na odcięciu składowej stałej, która spowodowałaby nieprawidłową pracę odtwarzacza. W tym celu zostały użyte dwa napięciowe źródła behavioral (B1 i B2), które odejmują wartość 2,5 od przebiegów z węzłów V(we_) i (V(a_wy_)).
Ponadto zapisywane sygnały powinny być na tyle długie, abyśmy mogli cokolwiek usłyszeć. Przyjęto więc założenie, że 1-sekundowy dźwięk powinien być wystarczająco długi. Choć wydaje się, że jedna sekunda to niewiele, dla symulatora jest to jednak poważne zadanie. Symulacja może trwać nawet do kilkudziesięciu minut. Aby przynajmniej częściowo przyspieszyć obliczenia została użyta komenda:
powodująca matrycowanie tylko wskazanych w niej węzłów. Po jej zastosowaniu nie ma wprawdzie możliwości podglądania przebiegów w innych węzłach, ale szybkość obliczeń znacząco się zwiększa.
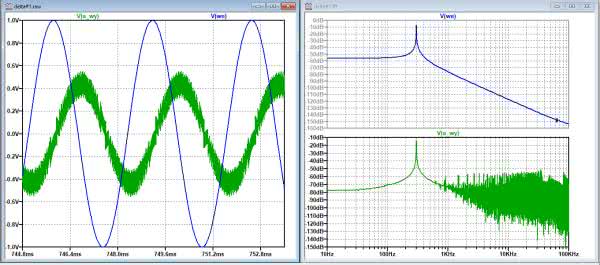
No cóż, na podstawie wzrokowej oceny nie można powiedzieć, aby jakość sygnału uzyskanego z takiego przetwornika była oszałamiająca, ale pamiętajmy, że jest to zaledwie model eksperymentalny, w dodatku tylko wirtualny. Przebiegi wejściowy wyjściowy zostały pokazane na rysunku 8. Uwzględniono na nich również analizę FFT.
Modulator sigma-delta
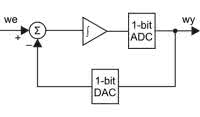
Jedną z najbardziej dokuczliwych wad modulatora delta są zniekształcenia przeciążeniowe. Powstają one w sytuacji, gdy szybkość zmian sygnału wejściowego jest większa niż szybkość narastania lub opadania przebiegu wyjściowego integratora. Układ nie nadąża wówczas śledzić przebiegu wejściowego, co finalnie objawia się ograniczeniem pasma. Koncepcja modulatora delta znana z lat 40. XX wieku została więc zmodyfikowana na początku lat 50. Zmiana polegała na dodaniu węzła sumacyjnego, do którego jest doprowadzany bezpośrednio sygnał wejściowy i przetworzony w 1-bitowym przetworniku DAC sygnał wyjściowy. Pamiętajmy, że sygnał ten był wcześniej całkowany, niesie więc informację o wartości średniej. Przebieg wyjściowy ma poza tym odwróconą fazę w stosunku do sygnału wejściowego, zatem węzeł sumacyjny de facto odejmuje doprowadzone do niego napięcia.
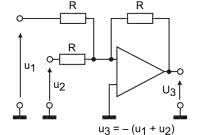
Schemat blokowy modulatora sigma-delta został pokazany na rysunku 9, na rysunku 10 natomiast została zamieszczona przykładowa realizacja modulatora sigma-delta, którą poddamy symulacji. Sumowanie sygnałów zapewniają rezystory R1 i R2, tak jak w klasycznym sumatorze z zastosowaniem wzmacniacza operacyjnego (rysunek 11). Sumowanie jest możliwe dzięki bardzo dużej (wielokrotnie większej od R1 i R2) oporności wejściowej wzmacniacza. Wszystkie „sztuczki” zastosowane do symulacji zostały powtórzone z poprzedniego eksperymentu. Po zdjęciu komentowania poleceń umieszczonych w lewym dolnym rogu możliwe jest zbadanie zniekształceń harmonicznych sygnału wyjściowego. Wyniki są odczytywane poleceniem View->SPICE Error Log. Zniekształcenia harmoniczne w symulacji wyniosły ok. 2%.
Można prościej
Robin Getz (Director of Systems Engineering w firmie Analog Devices) zaproponował w jednej ze swoich notek (wiki.analog.com) uproszczone rozwiązanie modulatora sigma-delta, w którym nie ma komparatora. Autor zastosował przerzutnik 74HC273 wykorzystując fakt, że poziom progowy dla tej serii układów jest równy połowie napięcia zasilającego. Tym samym przerzutnik 74HC273 pełni jednocześnie funkcję komparatora. Aby układ działał prawidłowo konieczne jest dołączenie wejścia nieodwracającego integratora (zbudowanego na wzmacniaczu operacyjnym AD8541) do napięcia 2,5 V odpowiadającego napięciu progowemu przerzutnika. Schemat układu pokazano na rysunku 12.
Weryfikacja praktyczna
Rozwiązanie z rysunku 10 zostało zweryfikowana praktycznie. Warunki pomiarowe nie uległy zmianie, przyjęto częstotliwość sygnału 300 Hz, częstotliwość próbkowania 200 kHz. Do pomiaru został użyty zestaw Analog Discovery 2, a w nim zasilacz +5 V, 2 kanały generatora arbitralnego, oscyloskop z włączoną funkcją FFT. Kształt przebiegu analogowego i cyfrowego uzyskanego w badanym przetworniku sigma-delta jest widoczny na rysunku 13. Tak jak w symulacji, w układzie rzeczywistym obserwujemy również odwrócenie fazy. Niestety parametry przyrządu są niewystarczające do obserwacji widma w szerokim zakresie częstotliwości z żądaną rozdzielczością.
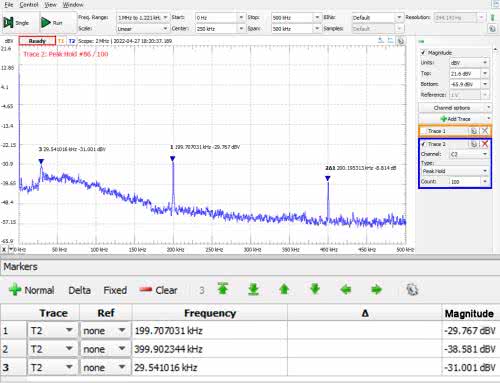
Dostępne w Analog Discovery 2 narzędzie – Spectrum w jednym ze swoich zakresów umożliwia pomiar widma do 100 MHz z rozdzielczością 1,221 kHz. W widmie nie zobaczymy zatem dokładnego prążka sygnału wejściowego, który niewątpliwie powinien się tu pojawić. Tak zmierzone widmo daje jednak jakieś pojęcie o zachowaniu się modulatora sigma-delta. Wyniki pomiaru zostały pokazane na rysunku 14. Wyraźnie widoczny jest prążek 200 kHz i jego harmoniczna 400 kHz, który odpowiada częstotliwości próbkowania. Widzimy również zwiększony poziom szumu w okolicach od ok. 25 kHz do ok. 180 kHz, z wyraźnym prążkiem 30 kHz.
Wnioski
Na pewno część Czytelników zauważyła, że w układzie został zastosowany zegar o częstotliwości wielokrotnie przewyższającej częstotliwość sygnału próbkowanego. Dla częstotliwości sygnału 200 Hz częstotliwość Nyquista jest równa zaledwie 400 Hz, tymczasem w układzie został zastosowany zegar 200 kHz. Czy to się opłaca?
Wielokrotne nadpróbkowanie (oversampling) to cecha charakterystyczna przetworników sigma-delta. Zabieg ten jest konieczny do uzyskania przebiegu cyfrowego o odpowiednio dużej rozdzielczości. Rozdzielczość przetwornika jest proporcjonalna do współczynnika nadpróbkowania.
Patrząc na przebieg wyjściowy widoczny na rysunku 13 Czytelnik może też mieć sporą wątpliwość widząc szum o wydawać by się mogło zbyt dużym poziomie. Owszem, taki szum faktycznie występuje, ale jego widmo zostało znacznie przesunięte w górę powyżej częstotliwości użytkowych (np. akustycznych). To dlatego o modulatorach sigma-delta mówi się, że są to układy z kształtowaniem szumu – nosie shaping.
Jarosław Doliński, EP

 Zaloguj
Zaloguj