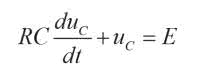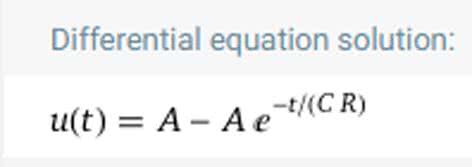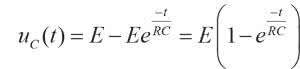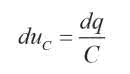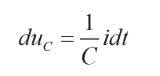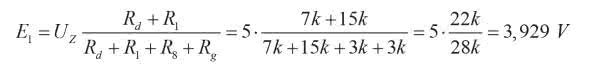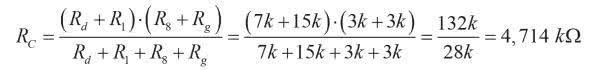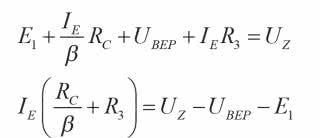Wprawdzie generatory były już omawiane w niniejszym cyklu, ale jest to temat o dużych walorach dydaktycznych, więc chętnie zastosujemy go ponownie. Naszym zadaniem jest zaprojektowanie generatora przebiegu trójkątnego. Zakładamy dość specyficzną budowę urządzenia, symulator zastosujemy więc przede wszystkim do sprawdzenia koncepcji. Działanie układu zależy od wielu parametrów. Nie wszystkie zastosowane w symulacji elementy elektroniczne będą odpowiadały elementom rzeczywistym. Należy więc przygotować się na to, że wyniki symulacji rozpatrywane ilościowo będą różnić się od pomiarów układu rzeczywistego. Zakładamy ponadto, że nie budujemy urządzenia w pełni użytkowego, a jedynie model, który dopiero po odpowiednich modyfikacjach mógłby uzyskać taki status.
Zasada działania generatora
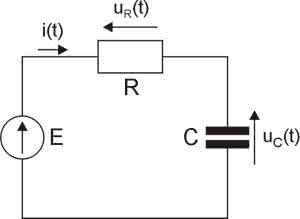
Zasada działania projektowanego generatora przebiegu trójkątnego jest oparta na ładowaniu kondensatora prądem stałym. Zwykle mamy do czynienia z ładowaniem pojemności ze źródła napięciowego przez istniejącą w obwodzie rezystancję. Jest to rozwiązanie trudne do przyjęcia w rozpatrywanym projekcie. Aby się o tym przekonać rozpatrzmy zjawiska zachodzące podczas ładowania kondensatora w typowym układzie RC (rysunek 1). Kondensator jest dołączony do źródła napięcia stałego przez rezystor r. Zakładamy, że w chwili początkowej napięcie na kondensatorze jest równe zero. Dla takiego obwodu możemy napisać równanie wyznaczające spadki napięć:
Ładunek zgromadzony w kondensatorze jest równy:
Prąd natomiast jest równy:
Zatem
czyli
Możemy już napisać równanie różniczkowe opisujące zjawiska w rozpatrywanym obwodzie RC.
Jest to liniowe równanie różniczkowe zwyczajne stopnia pierwszego o stałych współczynnikach. Chociaż nie jest to równanie nadmiernie skomplikowane, to jego rozwiązanie wymaga pewnych umiejętności z zakresu matematyki wyższej. Oczywiście nie będziemy aż tak głęboko zagłębiać się w niuanse teoretyczne i do rozwiązania równania posłużymy się znanym już z poprzednich odcinków programem WolphramAlpha. Formularz obliczeniowy tego programu znajdziemy pod adresem www.wolframalpha.com. Przy wprowadzaniu równania do programu musimy zamienić oznaczenie napięcia zasilającego. Tradycyjnie opisujemy je literą E, jednak WolphramAlpha może takie oznaczenie zinterpretować jako stałą matematyczną e. Literkę E zastępujemy więc literą A. Nasze równanie różniczkowe zapisane w programie ma więc postać jak na rysunku 2. Rozwiązanie równania pojawia się niemal natychmiast po naciśnięciu przycisku Compute Input (rysunek 3).
Wracamy do naszego zapisu:
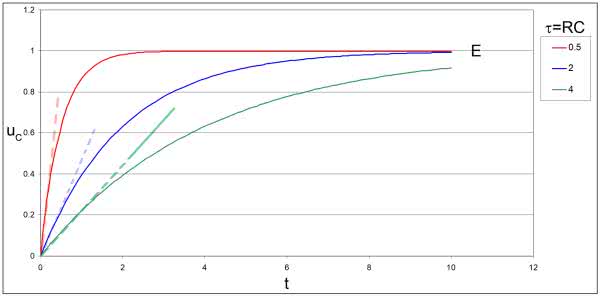
Równanie to potwierdza, że proces ładowania ze źródła stałonapięciowego nie jest liniowy. Napięcie na kondensatorze narasta wykładniczo tak, jak to przedstawiono na rysunku 4. Początkowe przyrosty zmian napięcia na kondensatorze odnoszone do pełnego napięcia E są niewielkie. Na tej podstawie można by przyjąć, że proces jest quasi liniowy. Powstałby jednak wówczas problem podejmowania decyzji o maksymalnym dopuszczalnym napięciu na kondensatorze. Powyżej takiej wartości granicznej ładowanie trudno by było dalej uznać za liniowe. Ponadto wraz ze zmianą częstotliwości generowanego sygnału, a więc zmianą stałej czasowej układu ładowania kondensatora, napięcie graniczne również by się zmieniało. Ostatecznie powyższą koncepcję budowy generatora odrzucamy. Ale nawet gdybyśmy ją przyjęli, musielibyśmy pogodzić się z faktem, że z matematycznego punktu widzenia krzywa ładowania miałaby jednak charakter wykładniczy, nie liniowy.
Zupełnie inne warunki ładowania wystąpią, jeśli zapewnimy ładowanie stałym prądem. W takim przypadku napięcie na kondensatorze jest opisane zależnością:
ale
czyli
Jeśli zostanie spełniony warunek stałości prądu ładowania kondensatora, to napięcie na kondensatorze można opisać zależnością:
Tym razem proces ładowania kondensatora jest już bezdyskusyjnie liniowy. Szybkość ładowania jest proporcjonalna do natężenia prądu i odwrotnie proporcjonalna do pojemności.
Jesteśmy coraz bliżej realizacji generatora. Pozostaje znalezienie metody przełączania źródła prądowego z trybu ładowania na rozładowanie kondensatora i odwrotnie. Najlepszym rozwiązaniem byłoby, aby zarówno ładowanie, jak i rozładowanie obsługiwało jedno źródło prądowe. No tak, ale w takim przypadku konieczne jest przełączanie kierunku wypływu prądu ze źródła, a to nie wydaje się zagadnieniem łatwym w realizacji. Na szczęście znamy rozwiązanie układowe zwane lustrem prądowym, które pozwoli nam zrealizować koncepcję.
Lustro prądowe
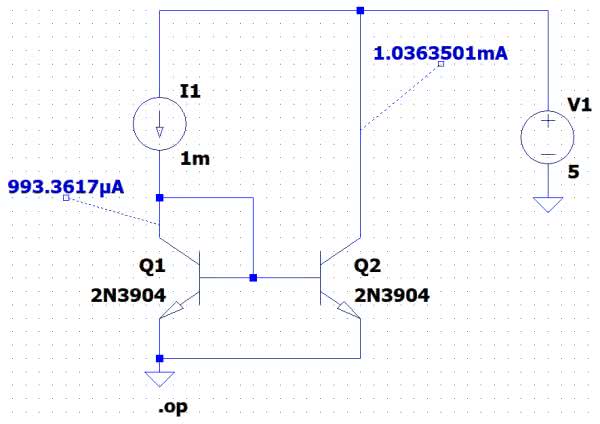
Schemat lustra prądowego został pokazany na rysunku 5. Składa się ono z dwóch tranzystorów Q1 i Q2. Ich złącza BE są połączone równolegle, a więc przy założeniu, że oba tranzystory mają jednakowe parametry i charakterystyki, prądy baz Q1 i Q2 powinny być równe. Zakładając równość współczynników wzmocnienia prądowego, także prądy kolektorów powinny być równe. Jeśli prąd kolektora tranzystora Q1 będzie pochodził ze źródła prądowego I1, to prąd kolektora tranzystora Q2 powinien być powtórzeniem prądu kolektora tranzystora Q1. Pomijamy przy tym rozpływ prądu I1 do baz obu tranzystorów, co spowoduje minimalną, w praktyce pomijalną asymetrię układu. Spełnienie wymienionych warunków jest możliwe najlepiej, jeśli zostaną zastosowane tranzystory zawarte w strukturze jednego układu scalonego. W najgorszym przypadku powinny to być tranzystory specjalnie dobierane (parowane), a dodatkowo należy zapewnić jak najbardziej zbliżone warunki temperaturowe.
W praktyce dyskretne tranzystory luster prądowych są często ze sobą sklejane. Ja do budowy lustra prądowego zastosowałem wygrzebany z głębokiej szuflady układ UL1111 zawierający 5 tranzystorów NPN, przy czym dwa z nich mają połączone emitery. Należy pamiętać, aby emiter wyprowadzony na nóżkę 13 znalazł się na najniższym potencjale występującym w układzie. Emiter ten jest dołączony do podłoża struktury. Jeśli potencjał podłoża będzie wyższy od któregokolwiek innego wyprowadzenia, układ nie będzie działał. Na rysunku 5 widoczne są wyniki symulacji stałoprądowej. Jak widać, prąd wpływający do lustra ma natężenie 1 mA, a wyjściowy prąd lustra ma natężenie 1,036 mA. Można więc z inżynierską dokładnością przyjąć, że oba prądy są równe.
Przyjęta koncepcja pracy generatora
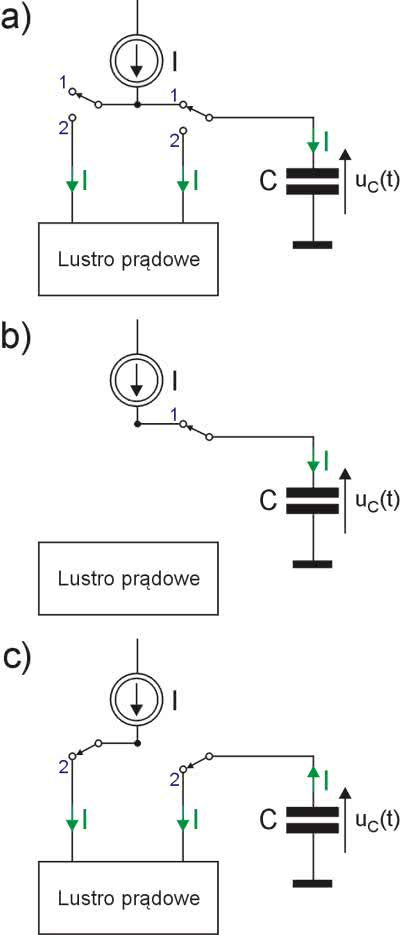
Koncepcję pracy generatora pokazano na rysunku 6a. Wyróżniamy dwa cykle. W pierwszym, przełącznik elektroniczny jest ustawiony w pozycji „1” (rysunek 6b). Kondensator jest ładowany ze źródła prądowego I, co powoduje, że napięcie na nim rośnie liniowo. W układzie musi być zastosowany komparator napięciowy (nieuwzględniony na rysunku), który po przekroczeniu napięć progowych na kondensatorze spowoduje przełączenie przełącznika elektronicznego. Po przekroczeniu górnego napięcia progowego nastąpi przełączenie w pozycję „2”. Prąd ze źródła I wpływa teraz do wejścia lustra prądowego, a do jego wyjścia zostaje jednocześnie przełączony kondensator. Powoduje to zmianę kierunku przepływu przez niego prądu. Napięcie na kondensatorze maleje, aż do wartości, w której przełącznik ponownie zmieni położenie do pozycji „1”. Tym samym cykl zostaje zakończony i układ staje się generatorem.
Przełącznik elektroniczny
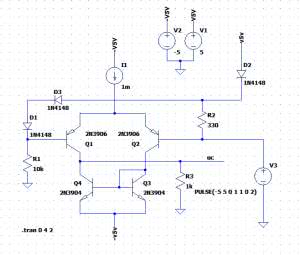
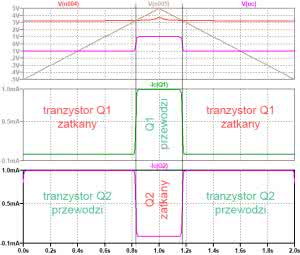
Przełącznik elektroniczny zbudujemy na tranzystorach dyskretnych Q1, Q2 (rysunek 7). Elementy I1, Q3 i Q4, to znane już z wcześniejszych rozważań źródło i lustro prądowe. Baza tranzystora Q1 jest utrzymywana na stałym potencjale wynikającym z napięcia zasilającego 5 V obniżonego o ok. 1,8 V przez diody D1...D3 (3×0,6 V). Diody pełnią funkcję przesuwników napięciowych. Napicie UB jest więc równe ok. 3,2 V. Jest to progowe napięcie przełączania. Dopóki napięcie na bazie Q1 jest wyższe niż na bazie Q2, tranzystor Q1 pozostaje w stanie wyłączenia (rysunek 8), przewodzi natomiast tranzystor Q2. Prąd I1 wpływa do lustra prądowego Q3-Q4 wywołując przepływ prądu przez rezystor R3 – 1 kΩ obciążający przełącznik. Prąd płynie przez ten rezystor w kierunku od masy do minusa zasilania. Występuje więc na nim spadek napięcia równy –1 V. W chwili, gdy napięcie na bazie Q2 zrówna się, a następnie przekroczy napięcie na bazie Q1, nastąpi zmiana przewodzenia tranzystorów – Q1 zacznie przewodzić, a Q2 zostanie wyłączony. Prąd będzie teraz płynął przez obciążenie w kierunku przeciwnym – od plusa zasilania do masy. Na rezystorze R3 wystąpi napięcie +1 V. Docelowo rezystor R3 zostanie zastąpiony kondensatorem.
Komparator
Jak już było powiedziane, w układzie generatora potrzebny jest komparator wyznaczający momenty przełączania kierunku przepływu prądu przez kondensator. Mechanizm ten zapewni okresowe przeładowywanie stałym prądem pojemności C, skutkiem czego na wyjściu generatora będzie wytwarzany przebieg trójkątny.
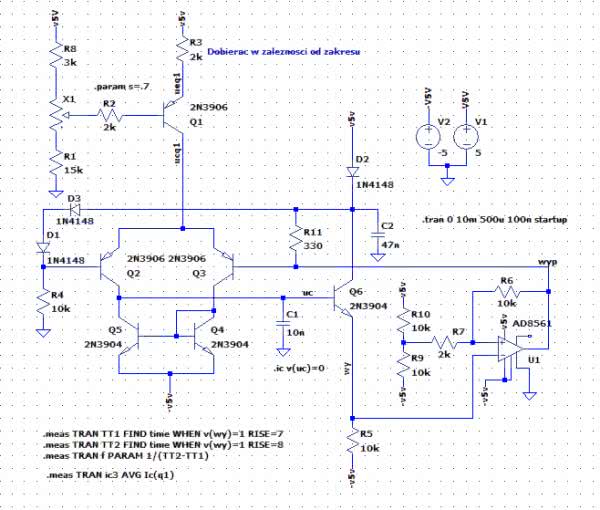
Wiemy, że po zastosowaniu w komparatorze dodatniego sprzężenia możliwe jest zaprogramowanie pożądanych wejściowych napięć progowych (a więc histerezy), po osiągnięciu których wyjście zmienia stan. Temat komparatorów był poruszany w 19. odcinku cyklu. Zaprezentowano w nim wzory pozwalające obliczyć powyższe parametry. W innym odcinku wspominałem też o zastosowaniu symulatora LTspice jako narzędzia zastępującego kalkulator podczas obliczeń projektowych. Upalna pogoda za oknem zachęca bardziej do lenistwa, niż wzmożonego wysiłku umysłowego, postanowiłem więc pójść na łatwiznę i elementy otoczenia komparatora (R6, R7, R9 i R10) wyznaczyłem metodą prób i błędów przy użyciu symulatora. Tym samym został zakończony cały etap projektowania. Można już narysować w edytorze symulatora LTspice pełny schemat generatora i przystąpić do symulacji (rysunek 9). Jak zwykle sytuacjom takim towarzyszą wzmożone emocje. Zadziała czy nie?
Ustawiamy położenie suwaka potencjometru regulującego częstotliwość przebiegu wyjściowego w pozycji np. 0,7. Punkt odniesienia (0) jest zaznaczony na schemacie kółeczkiem przy jednym z wyprowadzeń potencjometru (na schemacie dolnym). Potencjometr został zdefiniowany wcześniej jako element własny. W oknie jego parametrów (rysunek 10) można określić rezystancję i położenie suwaka. W tym przypadku położenie jest zadane parametrycznie parametrem s, któremu nadano wartość za pomocą polecenia .param s=.7.
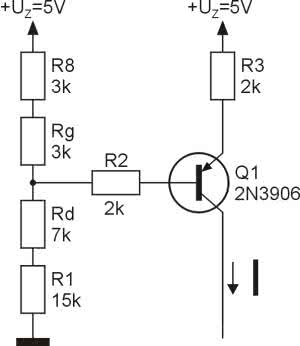
Ciekawość wygrywa jednak z lenistwem. Zanim uruchomimy symulację spróbujmy oszacować jakiego prądu możemy się spodziewać od naszego źródła (Q1)? Rysujemy schemat zastępczy dla suwaka w pozycji 0,7 – rysunek 11. Rezystor Rg to ta część rezystancji potencjometru, która jest nad suwakiem, Rd natomiast to rezystancja pod suwakiem. Naszym zadaniem jest wyznaczenie prądu kolektora tranzystora Q1.
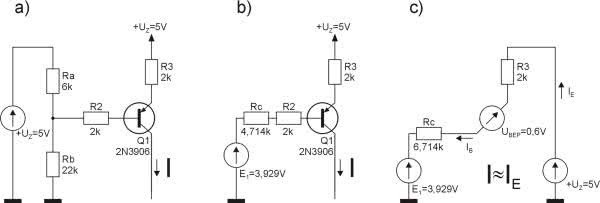
Najpierw zwijamy elementy R8, Rg, Rd, R1 i źródło napięciowe 5 V, tworząc źródło zastępcze E1 o rezystancji wewnętrznej równej równoległemu połączeniu R8+Rg i Rd+R1 (rysunek 12a i 12b).
Napięcie E1 jest równe:
Rezystancja wewnętrzna źródła E1 jest równa:
W kolejnym kroku dokonujemy pewnego uproszczenia rysunku 12b zastępując złącze baza-emiter źródłem napięciowym UBEP (rysunek 12c). Na pierwszy rzut oka coś na tym schemacie nie gra, gdyż prąd po lewej stronie źródła UBEP (IB) jest inny niż po prawej stronie (IE). Wynika to z nieuwzględnienia na tym rysunku złącza baza-kolektor tranzystora. W dalszych obliczeniach przyjmujemy, że prąd kolektora, czyli prąd naszego źródła, jest w przybliżeniu równy prądowi emitera, a prąd bazy IB jest β-krotnie mniejszy od prądu kolektora. Na tej podstawie można napisać równanie obwodu pokazanego na rysunku 12c:
czyli
Przyjęliśmy, że prąd emitera jest w przybliżeniu równy prądowi kolektora, więc możemy uznać, że obliczony wyżej prąd jest równy wydajności źródła prądowego I.
Symulacja
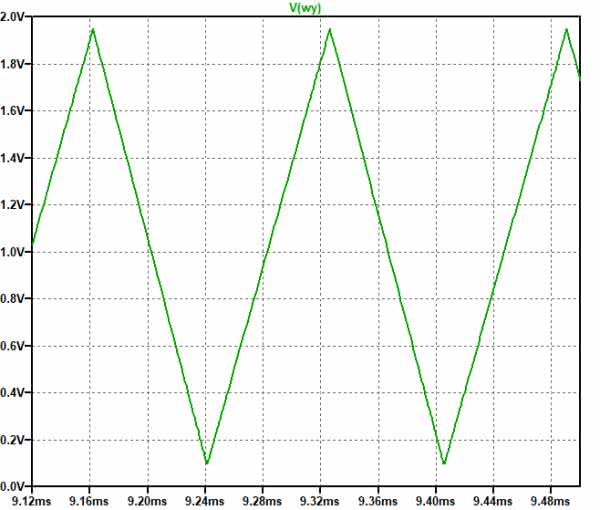
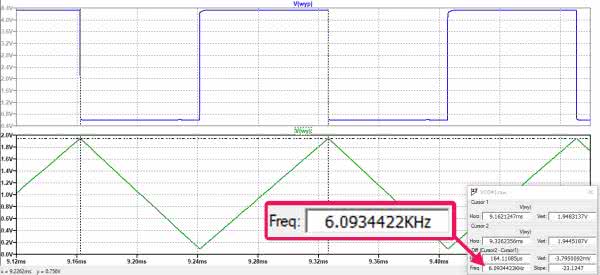
Nadeszła długo oczekiwana chwila, w której możemy uruchomić symulację. Będzie to symulacja czasowa .tran 0 10m 500u 100n startup. Spodziewamy się stanów nieustalonych po „włączeniu zasilania”, dlatego dane do analizy zaczynamy pobierać po 500 mikrosekundach od czasu t=0. Zapewniamy też dużą dokładność obliczeń ustalając parametr Maximum Timestep na 100 ns. Ponadto zaznaczamy opcję Start external DC supply voltages at 0V. Ładowany w układzie rzeczywistym kondensator prawdopodobnie będzie w stanie pełnego rozładowania w chwili uruchamiania generatora, zapewniamy więc zerowe napięcie początkowe również w kondensatorze symulowanym. Służy do tego komenda .ic v(uc)=0. Wcześniej należało nadać etykietę „uc” węzłowi, do którego jest dołączony kondensator. No cóż, zaczynamy. Po uruchomieniu symulacji pojawia się okno wykresu. Symulator nadal utrzymuje nas w niepewności. Wskazujemy węzeł wyjściowy „wy” i wszystko staje się jasne. Generator działa. Hura! Przebieg wyjściowy pokazano na rysunku 13.
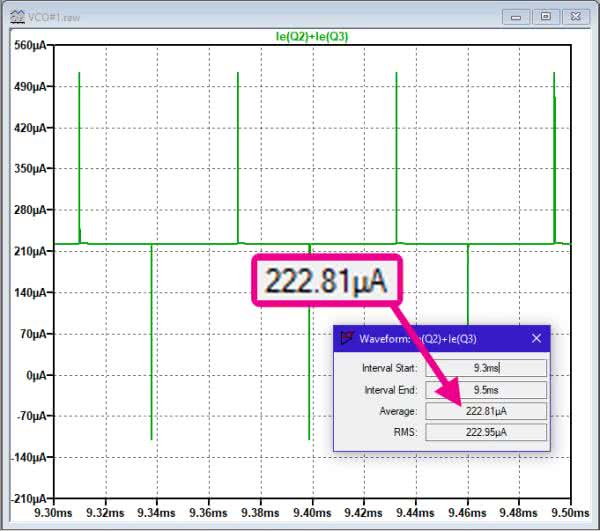
Sprawdźmy czy obliczony prąd źródła potwierdzi się w symulatorze. Ponownie uruchamiamy symulację, tylko tym razem naprowadzamy kursor myszy na połączenie między kolektorem Q1 a połączonymi emiterami Q2 i Q3, naciskamy przycisk H na klawiaturze i klikamy lewym przyciskiem myszki. Na ekranie ukazuje się wykres prądu pobieranego ze źródła Q1. Widoczne są na nim bardzo silne impulsy w chwilach przełączania (rysunek 14). Konieczne jest spore rozciągnięcie wykresu, aby możliwe było dokładniejsze przyjrzenie się szpilkom. Natężenie prądu ze źródła mierzymy naprowadzając kursor myszy na tytuł wykresu, po czym naciskamy przycisk Ctrl klawiatury komputera i klikamy lewym przyciskiem myszki. Pojawia się wówczas okno z danymi pomiarowymi (rysunek 14). Odczytujemy, że wartość średnia prądu jest równa 222,81 µA. Dla przypomnienia w obliczeniach wyszło nam 231 µA – nieźle.
Sprawdźmy jeszcze częstotliwość generowanego przebiegu odpowiadającego ustawieniu suwaka w pozycji 0,7. Można to z zadowalającą dokładnością zrobić wykorzystując kursory symulatora (rysunek 15), jednak my zastosujemy również komendy MEASURE. Warunkiem koniecznym do wykonania takiego pomiaru jest ustalenie na tyle długiego czasu, aby na ekranie było widocznych co najmniej 8 zboczy narastających sygnału. Nie jest to liczba, którą narzuca symulator, lecz parametr przyjęty arbitralnie. W pomiarach tego typu należy czekać na ustabilizowanie się przebiegu, w którym początkowo mogą występować jakieś stany nieustalone. Cały pomiar częstotliwości składa się z 3 komend. W pierwszej ustalany jest moment (czas), w którym napięcie wyjściowe przekracza jakiś przyjęty poziom, np. 1 V na 7. narastającym zboczu. Druga komenda wyznacza analogiczny moment dla 8. zbocza. Pozostaje już tylko obliczyć odwrotność różnicy tych czasów stanowiącej częstotliwość przebiegu. Obliczenie to wykonuje 3. komenda.
Pełny skrypt wygląda tak:
.meas TRAN TT1 FIND time WHEN v(wy)=1 RISE=7
.meas TRAN TT2 FIND time WHEN v(wy)=1 RISE=8
.meas TRAN f PARAM 1/(TT2-TT1)
Wynik, jak zwykle odczytujemy w logach błędów (rysunek 16) – tekst podświetlony na żółto.
Na zakończenie rozważań teoretycznych warto zauważyć, że jeśli wejściowy układ z potencjometrem zastąpilibyśmy wejściem doprowadzającym jakieś napięcie sterujące DC, uzyskalibyśmy funkcjonalność generatora przestrajanego napięciem (VCO).
Kończą się dobre wiadomości
Jak zwykle po obliczeniach i symulacji nadeszła pora weryfikacji projektu w układzie rzeczywistym. Mimo, że projekt zawiera sporo elementów, całość montujemy na breadboardzie. Pozostając w stylu vintage wygrzebałem ze swojej przepastnej szuflady stare tranzystory PNP – chyba BC177. Trudno stwierdzić typ, gdyż napisy na metalowych obudowach już dawno się wytarły. Tranzystory tego typu były dość powszechnie stosowane w epoce, w której popularnością cieszył się układ UL1111. Nieco kontrastujący jest dla nich już jak najbardziej współczesny komparator AD8561.
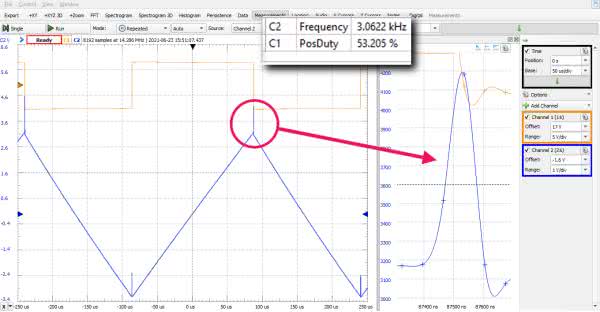
Układ jest już zmontowany. Przystępujemy do pomiarów. Dołączmy do komputera zestaw „Analog Discovery 2” i uruchamiamy program WaveForms. Generator zasilamy z zasilacza AD2. Wykorzystujemy obie sekcje: napięcia dodatniego +5 V i ujemnego –5 V. Nie zapomnijmy połączyć ze sobą mas AD2 i generatora. Włączamy zasilanie i... są dwie wiadomości, tradycyjnie jedna dobra, druga zła. Zaczynamy od dobrej: układ generuje. Na wyjściu pojawia się przebieg trójkątny, mniej więcej taki, jakiego się spodziewaliśmy. Niestety, druga wiadomość brzmi: nic poza tym nie zgadza się z symulacją. Przede wszystkim inna jest amplituda przebiegu wyjściowego. Przy ustawieniu suwaka w pozycję 0,7 wystąpiła tak znaczna asymetria sygnału wyjściowego, że praktycznie trudno by było zakwalifikować taki przebieg jako użytkowy. Poprzez ustawienie suwaka asymetrię można skorygować do około 53% (powinno być 50%), ale zadaniem potencjometru jest regulacja częstotliwości, a nie symetrii.
Asymetrię można tłumaczyć błędem wprowadzanym przez lustro prądowe. W rzeczywistości prąd wpływający do lustra nie jest idealnie odtwarzany na wyjściu, co powoduje, że kondensator jest rozładowywany minimalnie innym prądem niż prąd ładowania.
W sygnale wyjściowym występują ponadto bardzo duże szpiki w chwilach przełączania. Są one widoczne w powiększeniu na rysunku 17. Symulator nie wykrył tego zjawiska. Zakłócenia tego typu wynikają z nierównoczesności przechodzenia ze stanu zatkania do stanu przewodzenia przez tranzystory Q2 i Q3. Przyczyną mogą być różnice charakterystyk tranzystorów, a także minimalne skoki napięciowe na bazie tranzystora Q2. W układzie zmontowanym na breadboardzie zabrakło kondensatorów blokujących zasilanie.
Wnioski na zakończenie
Czy wobec różnic pomiędzy symulacją i pomiarami układu rzeczywistego można uznać symulator LTspice za narzędzie przydatne w rękach projektanta? Jest to często zadawane pytanie przez wielu sceptyków. Oczywiście, chcielibyśmy aby wyniki symulacji i pomiarów pokrywały się w 100 procentach, ale w większości przypadków, może poza jakimiś zupełnie elementarnymi obwodami, jest to raczej niemożliwe. Problemy zaczynają się, gdy na pracę układu rzeczywistego mają wpływ okoliczności trudne do przewidzenia i uwzględnienia w symulacji. Przykładem jest choćby wpływ zakłóceń pochodzących z otoczenia, szumy i interferencje, rozpływy prądów w różnych węzłach obwodu rzeczywistego, a przede wszystkim jakość modeli elementów wchodzących w skład badanego układu. Często, z braku jakichkolwiek modeli elementów zastosowanych w urządzeniu użytkownicy symulatora podkładają modele innych, mniej lub bardziej podobnych elementów. Przyznam ze skruchą, że tak postąpiłem w tym odcinku. Zamiast modeli tranzystorów BC177 i tranzystorów układu UL1111 zastosowałem modele tranzystorów 2N3906 (PNP) i 2N3904 (NPN). Model komparatora pochodzi ze strony producenta – firmy Analog Devices.
W opisywanym zagadnieniu przydatność symulatora LTspice była jednak bezsprzeczna. Przystępując do projektowania generatora w zasadzie liczyłem się z tym, że nie uzyskam prawidłowych wyników ilościowych, chodziło jednak głównie o weryfikację koncepcji. Nie ukrywam, że do zaprezentowanego wyniku końcowego konieczna była analiza kilku innych, zbliżonych wariantów projektu. Należy jednak jeszcze raz zaznaczyć, że założeniem nie była budowa urządzenia użytkowego, a jedynie pokazanie przykładowej metody projektowania.
Symulatory są stosowane w wielu dziedzinach techniki i życia codziennego, nie tylko przez projektantów urządzeń. Szkolą się na nich i podtrzymują umiejętności piloci, kierowcy Formuły 1, maszyniści lokomotyw, kapitanowie statków morskich i jachtów. Korzystają z nich nawet modelarze sprawdzający czy np. budowany model samolotu będzie miał szansę wznieść się w powietrze i jak będzie reagował na elementy sterujące (pełna analogia z naszym generatorem). Jednocześnie, z uwagi na możliwe rozbieżności, absolutnie niedopuszczalne jest wydawanie ponad wszelką wątpliwość jakichkolwiek wniosków na temat różnych zdarzeń badanych z zastosowaniem symulacji.
Jest to już ostatni artykuł trwającego 2 lata cyklu. Mam świadomość, że mimo tak długiego czasu nie wszystkie zagadnienia zostały poruszone. Być może nadarzą się jeszcze jakieś okazje by wyrywkowo powracać do takich tematów.
Jarosław Doliński, EP

 Zaloguj
Zaloguj