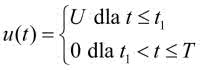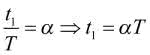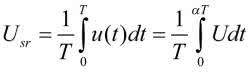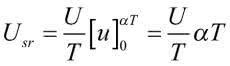Symulacja i pomiar, czyli LTspice i Analog Discovery 2 w rękach konstruktora (11). Modulacja PWM

W początkach elektroniki, z przyczyn oczywistych, rozwijane były modulacje analogowe (AM, FM). Do czasu pojawienia się pierwszych urządzeń cyfrowych nie było większej potrzeby opracowywania specjalnych rodzajów modulacji. Istniejąca już telegrafia nie stawiała nazbyt wygórowanych wymagań. Urządzenia transmisji danych konstruowane już w czasach techniki cyfrowej wykorzystywały i nadal wykorzystują różne media (radio, kabel, światłowód itd.), tym samym narzucają o wiele bardziej złożone rodzaje modulacji. Pojawiła się potrzeba zwiększania szybkości przesyłania danych, a także zwiększania liczby kanałów w jednym torze transmisyjnym. Powstało wiele nowych rodzajów modulacji, wykaz najczęściej obecnie stosowanych zestawiono w ramce. My zajmiemy się w artykule modulacją dość specyficzną. Nie opracowano jej do urządzeń komunikacyjnych.

Modulacja PWM

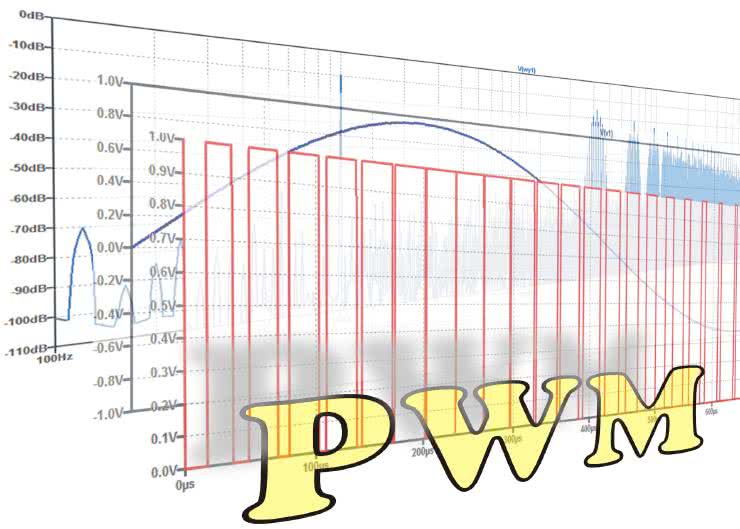
PWM (Pulse Width Modulation) zaliczamy do modulacji cyfrowych. Oznacza to, że efektem działania modulacji jest przebieg cyfrowy. Jest to przebieg prostokątny o dwóch dyskretnych poziomach i skończonym zbiorze wartości współczynnika wypełnienia. Te specyficzne, typowo cyfrowe własności przebiegu PWM decydują o... analogowych zastosowaniach modulacji PWM. Jak to możliwe?

Rysunek 1. Przebieg prostokątny z zaznaczoną wartością średnią zależną od współczynnika wypełnienia

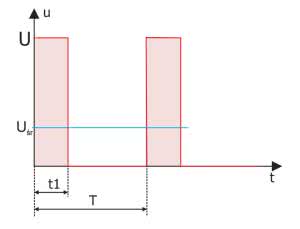
Rozpatrzmy przebieg prostokątny, w którym okres powtarzania impulsów jest równy T, ich amplituda jest stała i równa U, a czas trwania impulsu jest równy t1 (rysunek 1). Przebieg jest opisany zależnością:

Jak wynika z rysunku 1, czas t1 występujący w powyższym wyrażeniu jest związany z okresem przebiegu zależnością:

Parametr a jest nazywany współczynnikiem wypełnienia. Wartość średnia sygnału jest równa:

Rozwiązaniem tej całki jest:

Ostatecznie:

Uzyskaliśmy w ten sposób bardzo ważny wniosek: zmieniając współczynnik wypełnienia przebiegu prostokątnego, wpływamy na wartość średnią napięcia. Co więcej, jest to zależność liniowa. W tym momencie otwiera się szereg zastosowań w urządzeniach analogowych: począwszy od regulacji jasności świecenia żarówki lub diody LED, regulacji obrotów silnika, regulacji mocy grzałki, skończywszy na zakodowaniu przebiegiem PWM sygnału akustycznego, co będzie tematem eksperymentu, który przeprowadzimy. Warto wspomnieć, że technika ta jest stosowana w akustycznych wzmacniaczach mocy klasy D. Są nawet produkowane specjalne układy scalone stanowiące niemal kompletne wzmacniacze audio.

Eksperyment – modulacja PWM z zastosowaniem sygnału akustycznego

Naszym zadaniem będzie zakodowanie sygnału sinusoidalnego w przebiegu prostokątnym poprzez zastosowanie modulacji PWM. Do eksperymentu użyjemy narzędzi dostępnych w dobrze już nam znanym przyrządzie Analog Discovery 2. Dla uproszczenia przyjmiemy, że sygnał sinusoidalny będzie miał stałą częstotliwość i amplitudę.

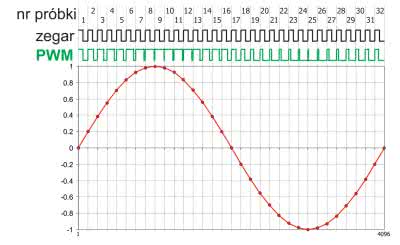
Jak już wiemy, PWM jest zaliczana do modulacji cyfrowych, w procesie modulacji musi więc wystąpić próbkowanie. Przyjmiemy, że na jeden okres sinusoidy będą przypadały 32 próbki. Zastanówmy się, jak to zrealizować? Pamiętamy, że współczynnik wypełnienia przebiegu prostokątnego jest proporcjonalny do wartości średniej napięcia za okres. Przyjmijmy teraz odwrotny tok rozumowania. Niech napięcie decyduje o współczynniku wypełnienia. Zgodnie z przyjętym wcześniej założeniem na jeden okres sinusoidy przypadną 32 okresy przebiegu prostokątnego. Wypełnienie w każdym jego cyklu powinno zmieniać się proporcjonalnie do chwilowej wartości sinusoidy przypadającej na daną próbkę (rysunek 2).

Rysunek 2. Ilustracja zasady tworzenia przebiegu PWM

Przyjmujemy ponadto, że wypełnienie 1/2 będzie odpowiadało zerowemu napięciu sinusoidy, wypełnienie 1 odpowiada wartości maksymalnej sinusoidy (dodatniej), a wypełnienie 0 wartości minimalnej (ujemnej).

Przebieg prostokątny modulowany sinusoidą jest taktowany przebiegiem zegarowym o częstotliwości 32 razy większej od częstotliwości sinusoidy. Zasadę działania pokazano na rysunku 2, nadal jednak nie wiemy, jak tę koncepcję zrealizować. Tym razem nie zbudujemy fizycznego układu zawierającego generator sinusoidalny modulujący falę prostokątną uzyskaną z innego generatora. Zmodulowany przebieg zostanie wygenerowany bezpośrednio w generatorze arbitralnym Analog Discovery 2. Nie będziemy rozpatrywać budowy układów realizujących funkcję PWM, a zajmiemy się jedynie pokazaniem niektórych własności sygnału tak zmodulowanego. Obecnie, gdy na co dzień, nawet w najprostszych układach elektronicznych stosujemy mikrokontrolery, generowanie przebiegu PWM nie jest większą trudnością.

Wstępna symulacja w LTspice

Dane dla generatora przygotujemy w Excelu. Zanim zaczniemy pracę w arkuszu, rozpatrzmy metodę układową, która mogłaby być zastosowana do generowania sygnału PWM. Metodę tę zastosujemy w obliczeniach excelowych.

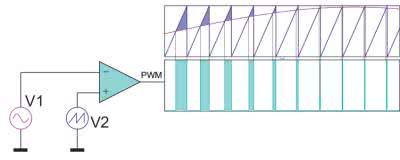
Potrzebne będą: generator przebiegu piłokształtnego (tzw. integrator wytwarzający przebieg liniowo narastający od wartości minimalnej (–1) do maksymalnej (+1) w czasie równym odstępowi między próbkami), źródło sygnału modulującego (sinusoida o okresie T) i amplitudzie 0,95 umownych jednostek i komparator porównujący dwa napięcia. Przyjrzyjmy się, jak działa komparator. Można powiedzieć, że jest to specyficzny wzmacniacz operacyjny pracujący z otwartą pętlą, co w praktyce oznacza przebywanie wyłącznie w stanie nasycenia lub odcięcia. Scalone komparatory są konstruowane pod kątem minimalizacji czasu przeskoku z jednego stanu do drugiego.

Rysunek 3. Przykładowa realizacja układu PWM

Przykładową realizację układu PWM wytwarzającego przebieg zmodulowany sygnałem sinusoidalnym pokazano na rysunku 3. Jeśli napięcie V2 na wejściu nieodwracającym komparatora jest większe od napięcia na wejściu odwracającym V1, wyjście komparatora przyjmuje stan wysoki, w przeciwnym przypadku wyjście pozostaje w stanie niskim. Podając na wejście nieodwracające przebieg narastający liniowo, komparator będzie przyjmował niski stan wyjściowy, dopóki napięcie to nie przewyższy napięcia na wejściu odwracającym. Nagły skok napięcia V2 wyznaczający koniec jednej próbki i początek następnej powoduje zawsze przejście komparatora do stanu niskiego. Tym samym uzyskujemy przebieg PWM, w którym wypełnienie przebiegu prostokątnego w każdym cyklu odpowiada chwilowej wartości przebiegu modulującego.

Rysunek 4. Symulacja układu PWM w programie LTspice

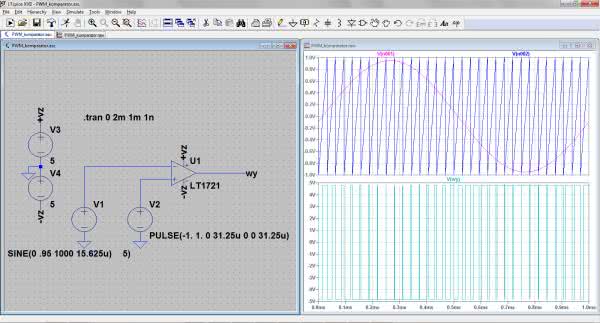
Aby upewnić się, czy idea jest poprawna, układ taki możemy zasymulować w programie LTspice. Na rysunku 4 pokazano schemat i wynik symulacji. Przyjęto, że przebieg sinusoidalny ma częstotliwość 1 kHz, w związku z czym piła powinna mieć częstotliwość 32 razy większą, czyli 32 kHz. Okres przebiegu piłokształtnego jest więc równy 31,25 μs. Przebieg ten narasta od wartości –1 do 1 w czasie 31,25 μs i taki ma okres powtarzania. Jest to równoważne z zerowym czasem przerzutu ze stanu wysokiego do niskiego. W rzeczywistości jest to niemożliwe, ale na potrzeby symulacji możemy sobie na to pozwolić.

Wyjaśnienia wymaga jeszcze czas opóźnienia wprowadzony w parametrach źródła V1. Jest on równy 15,625 μs, co odpowiada połowie okresu przebiegu piłokształtnego. Zabieg ten jest potrzebny, aby zapewnić założenie, że dla zerowej wartości sinusoidy wypełnienie powinno być równe 1/2. Ten rozbiegowy fragment symulacji pomijamy, ustalając czas analizy na 2 ms i rozpoczęcie wyświetlania wyników od 1 ms.

W materiałach dodatkowych do artykułu dołączono plik PWM_komparator.asc z powyższą symulacją. Jest też analogiczna symulacja PWM_bv.asc z zastosowaniem napięciowego źródła behawioralnego realizującego funkcję: V=if(V(V2) > V(V1),1,0). Jest to dobra metoda testowania idei, bez uwzględniania parametrów układów elektronicznych (komparatorów, wzmacniaczy operacyjnych itp.). W symulacji zastosowano długi czas analizy, który jest potrzebny do uzyskania widma sygnału PWM o odpowiednio dużej rozdzielczości. Należy więc pogodzić się z długim czasem obliczeń. Będzie jeszcze o tym mowa.

Przygotowanie sygnału PWM w Excelu

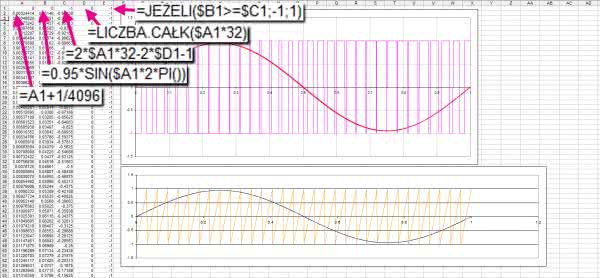
Powyższą, sprawdzoną w symulacji ideę zastosujemy w arkuszu kalkulacyjnym (pwm_obliczenia.xls), w którym zostaną utworzone dane dla generatora arbitralnego. Przyjmujemy, że pełny okres przebiegu powinien wypełnić całą pamięć generatora – 4096 danych. Krok czasu jest więc równy 1/4096 umownych jednostek. Na razie nie musimy podawać konkretnych wartości, gdyż będą one ustalane podczas uruchamiania generatora. W kolumnie A Excela znajdą się czasy poszczególnych elementów przebiegu odnoszone do okresu (rysunek 5); czyli A1=0, A2=A1+1/4096, A3=A2+1/4096 itd. aż do A4096. Kolumna B zawiera funkcję sinus, a więc nasz przebieg modulujący: B1=0.95*SIN($A1*2*PI()).

Rysunek 5. Przygotowanie danych dla generatora arbitralnego w Excelu

Przyjęto amplitudę 0,95, zostawiając mały margines dla wartości maksymalnej i minimalnej.

Do wygenerowania przebiegu PWM jest jeszcze potrzebny przebieg piłokształtny opisany funkcją liniową y=a*x+b. Współczynnik nachylenia a jest stały i przy założeniu, że długość próbki (szerokość ząbka) jest równa 1, a wysokość ząbka jest równa 2 (od –1 do +1), współczynnik a przybiera wartość 2. Dla każdego ząbka zmienia się jego przesunięcie w osi pionowej. Jest za to odpowiedzialny współczynnik b. Do obliczenia współczynnika b konieczna jest znajomość numeru próbki, jest ona obliczana w kolumnie D formułą: D1=LICZBA.CAŁK($A1*32). Jest ona kopiowana aż do komórki D4096. I teraz następuje najtrudniejsza operacja definiująca przebieg piłokształtny na podstawie przedstawionych obliczeń. Formuła ta jest umieszczona w kolumnie C i ma następujący zapis:

C1=2*$A1*32-2*$D1-1. Składnik –1 jest związany z zapewnieniem wypełnienia 1/2 dla zerowej wartości funkcji sinus.

W ostatniej kolumnie E zawarto definicję przebiegu PWM, którą skopiujemy do pamięci generatora arbitralnego Analog Discovery 2. W polach kolumny E znajdują się formuły: E1=JEŻELI($B1>=$C1;-1;1). Możemy powiedzieć, że wyrażenie to jest matematycznym odpowiednikiem komparatora z wcześniejszego przykładu. Obliczenia wykonane w Excelu wraz z wykresami pokazano na rysunku 5.

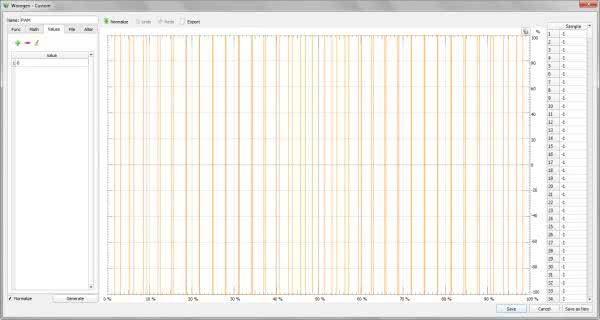
Wszystko jest już gotowe, możemy przystąpić do prób układu rzeczywistego. Otwieramy program WaveForms, a w nim uruchamiamy generator arbitralny. Wybieramy tryb użytkownika (Custom) i otwieramy edycję nowego przebiegu (New). Teraz wracamy na chwilę do Excela. Kopiujemy do pamięci podręcznej kolumnę E (zaznaczamy kolumnę E i naciskamy Ctrl-C). W oknie edytora przebiegów wprowadzamy kursor na pierwszy wiersz kolumny Sample i naciskamy Ctrl-V. W rezultacie dane z Excela zostały skopiowane do generatora arbitralnego. W oknie grafiki powinniśmy zobaczyć przebieg PWM, w którym jest zakodowana sinusoida (rysunek 6). Rzeczywiście, wszystko wskazuje na to, że nasze działania okazały się poprawne. Pozostaje więc uruchomić generator i sprawdzić efekt pracy.

Rysunek 6. Przebieg PWM przygotowany w edytorze generatora arbitralnego Analog Discovery 2

Dołączamy wyjście generatora arbitralnego do wejścia 1. kanału oscyloskopu. Parametry sygnału wyjściowego ustalamy następująco:

• Frequency = 1 kHz
• Sample Rate = 4,096 MHz (ten parametr jest obliczany automatycznie)
• Amplitude = 100 mV
• Offset = 0 V
• Phase = 0°

W oscyloskopie natomiast wybieramy:

• Base = 200 μs/div
• Offset = 0 V
• Range = 50 mV/div

Problematyczne może być wybranie dogodnego trybu synchronizacji. Tradycyjna, najczęściej stosowana synchronizacja zboczem zupełnie nie zda egzaminu. Tą metodą nie uzyskamy stabilnego oscylogramu.

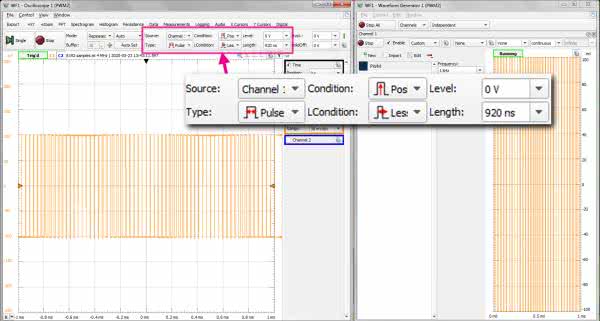
Oscylogram będzie latał po ekranie we wszystkie strony. Okazuje się, że dla częstotliwości 1 kHz ustawionej w generatorze najwęższy impuls ma czas trwania nie większy niż 920 ns. Wybieramy zatem synchronizację typu Pulse, dla której ustalamy parametry Conditions = Less i Lenght = 920 ns i Condition = Positive. Po uruchomieniu generatora i oscyloskopu pojawia się stabilny oscylogram jak na rysunku 7. Bingo! Mamy to!

Rysunek 7. Przebieg PWM obserwowany za pomocą oscyloskopu

Widzimy piękny przebieg PWM przypominający ten z Excela. Czy wynik nas zaskakuje? Gdzie jest sinusoida?

Analog Discovery 2 ma wyjście słuchawkowe, za pomocą którego możemy podsłuchiwać – w dosłownym znaczeniu – sygnał z obu kanałów generatora. Dołączmy więc słuchawki i posłuchajmy.

Tego nie da się pokazć na papierze, ale jeśli ktoś powtórzy samodzielnie eksperyment, usłyszy w słuchawkach ton o częstotliwości 1 kHz.

A co z przebiegiem prostokątnym, który widzimy na oscylogramie? Można powiedzieć – dość dziwna sytuacja: widzimy prostokąt, a go nie słyszymy, nie widzimy sinusoidy, a ją słyszymy. To wszystko dzieje się na skutek ułomności naszego słuchu. Jak pamiętamy, częstotliwość przebiegu prostokątnego jest 32-krotnie wyższa od częstotliwości sinusoidy. Częstotliwość 1 kHz ustawiona w generatorze dotyczy całego przebiegu PWM, a więc obejmuje jeden okres sinusoidy. Oznacza to, że przebieg sinusoidalny ma częstotliwość 1 kHz, a prostokątny 32 kHz.

Oczywiste jest więc, że prostokąta nie słyszymy. Ucho natomiast stanowi swego rodzaju filtr dolnoprzepustowy, którego częstotliwość graniczną wyznaczają własności naszego słuchu. Dla jednych będzie to kilkanaście kiloherców, osoby starsze mogą mieć problem ze słyszeniem dźwięków już powyżej 8 czy nawet 5 kHz. Jak to wygląda w rzeczywistości, możemy przekonać się, obserwując widmo sygnału PWM za pomocą funkcji FFT.

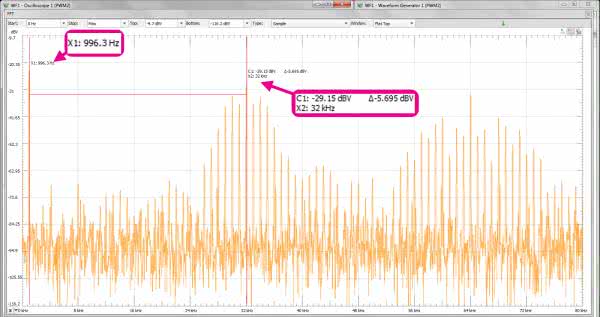
Uwzględniając własność tej funkcji dotyczącą rozdzielczości widma, wydłużamy czas akwizycji sygnału, zmieniając parametr Base oscyloskopu do 5 ms/dz. Czas akwizycji pełnego rekordu jest wówczas równy 5 ms/dz.×10 dz.=50 ms. Rozdzielczość widma jest wówczas równa 1/50 ms=20 Hz. Jest to wartość przybliżona, ponieważ rekord akwizycji oscyloskopu Analog Discovery 2 ma długość 8192 dane i przy tych nastawach oscyloskop próbkuje sygnał z częstotliwością 160 kHz. Oznacza to, że rzeczywisty czas akwizycji jest równy 8192/160000=51,2 ms, a więc rzeczywista rozdzielczość widma funkcji FFT jest równa 19,53 Hz. Są to jednak niuanse, którymi nie będziemy sobie zaprzątać głowy.

Rysunek 8. Widmo sygnału PWM obserwowane funkcją FFT

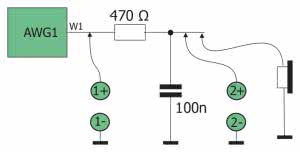
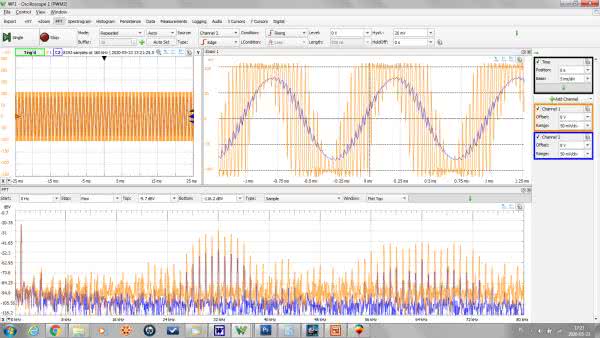
Widmo sygnału pokazano na rysunku 8. Wyraźnie widoczny jest prążek sinusoidy 1 kHz (w FFT 996,3 kHz) oraz widmo prostokąta 32 kHz wraz z harmonicznymi. Co trzeba zrobić, żeby zobaczyć sinusoidę na oscyloskopie? Oczywiście, zastosować filtr. Wykonamy prosty filtr 1. rzędu o częstotliwości granicznej ok. 3,3 kHz, tak jak to pokazano na rysunku 9. Widoczne na schemacie słuchawki mogą stanowić zbyt duże obciążenie dla tego układu. Jeśli tak się okaże w praktyce, punkt dołączenia słuchawek należy traktować jako wyjście filtru, które łączymy z wejściem dowolnego wzmacniacza akustycznego. Przebieg wyjściowy po odfiltrowaniu pokazano na rysunku 10. W oknie „Zoom” jest na nim doskonale widoczna nasza sinusoida zanieczyszczona nieodfiltrowanymi resztkami prostokąta. Dołączono ponadto widmo FFT, na podstawie którego widzimy skuteczność działania filtru.

Rysunek 9. Układ do „podsłuchiwania” sygnału PWM

Mając na uwadze filtrujące działanie naszego słuchu, można zadać pytanie: czy konieczne jest filtrowanie sygnału akustycznego w układach PWM? Niestety, odpowiedź jest twierdząca. To, że my nie słyszymy wyższych składowych widma, nie oznacza, że ich nie ma. W układach obróbki sygnału mogą one powodować występowanie niepożądanych interferencji i powstawanie wielu nieoczekiwanych składowych. Każdy, kto miał do czynienia ze wzmacniaczami akustycznymi, wie doskonale, czym może skończyć się dołączenie kolumn do wzbudzonego wzmacniacza.

A przecież te wysokie składniki widma można traktować analogicznie do wysokich częstotliwości, często ponadakustycznych, generowanych przez wzbudzony wzmacniacz. Na szczęście głośniki wysokotonowe są zwykle tańsze od niskotonowych. Ich wymiana to jednak niepotrzebne zajęcie i zbędne koszty.

Efekty chciane czy niechciane

O jakości dźwięku generowanego metodą modulacji PWM można przekonać się, porównując go z czystym dźwiękiem uzyskiwanym z drugiego kanału generatora arbitralnego Analog Discovery 2. Zmniejszając częstotliwość sygnału w 1. kanale, automatycznie zmniejszamy częstotliwość przebiegu prostokątnego. Dla dostatecznie niskich częstotliwości fala prostokątna stanie się wyraźnie słyszana. Pojawią się ciekawe interferencje, które w większości przypadków będą zdecydowanie niepożądane, ale na przykład dla kompozytorów „el muzyki” (mam nadzieję, że nie jest to termin zastrzeżony przez Jerzego Kordowicza) mogą okazać się ciekawą inspiracją.

PWM i akustyka

Zalety modulacji PWM w aplikacjach regulacji mocy są niekwestionowane. Dzięki zastosowaniu tej metody znacznie upraszczają się rozwiązania układowe, a co najważniejsze, jest to metoda zapewniająca bardzo wysoką sprawność regulacji. Modulacja PWM w akustyce może już budzić pewne wątpliwości, głównie ze względu na dużą liczbę generowanych harmonicznych i spore zniekształcenia. Z tego względu wzmacniacze mocy na razie raczej nie są obiektem zainteresowań audiofilów, znajdują natomiast zastosowanie w zakresie car audio, gdzie sprawdzają się bardzo dobrze. Scalone wzmacniacze klasy D są produkowane przez wiele firm. Przykładowo, w ofercie STMicroelectronics można znaleźć wzmacniacze o mocy od 20 W do 100 W (np. TDA7491HV, TDA7492, TDA7498MV).

Rysunek 10. Odfiltrowany przebieg PWM

Z powyższego opisu można wnioskować, że konstrukcja wzmacniacza akustycznego klasy D jest bardzo prosta. Układy komercyjne mają jednak budowę znacznie bardziej skomplikowaną. Konstrukcja musi uwzględniać takie zjawiska, jak straty mocy w układach przełączających (np. tranzystorach MOSFET), które rosną wraz ze wzrostem częstotliwości przełączania. Nie bez znaczenia jest też utrzymanie stałej częstotliwości przebiegu prostokątnego. Jego drżenie (jitter) może wprowadzać słyszalne zniekształcenia wyjściowego sygnału analogowego. Niezwykle ważne jest skuteczne tłumienie sygnału przełączającego oraz jego harmonicznych, szczególnie wyższych rzędów. Jest to związane z koniecznością spełniania wyśrubowanych norm dotyczących kompatybilności elektromagnetycznej. Producenci bezustannie pracują nad ulepszaniem konstrukcji wzmacniaczy klasy D i wszystko wskazuje na to, że wkrótce będzie to jedna z podstawowych klas tranzystorowych wzmacniaczy mocy. Lampy mogą się czuć jednak niezagrożone. A my w kolejnym odcinku, jak dobrze w tych trudnych czasach pójdzie, zajmiemy się bardzo teoretycznymi zagadnieniami: rachunkiem operatorowym i przekształceniami Laplace’a.

Jarosław Doliński, EP