Człowiekiem, któremu w dużej mierze zawdzięczamy dzisiejszą wiedzę o harmonicznych jest fizyk i matematyk Jean Baptiste Joseph Fourier (21.03.1768 - 16.05.1830, fotografia 1).
Nie jest to zresztą pierwsza okazja do wspomnienia tego naukowca. Za życia nie mógł zdawać sobie sprawy z tego, jak wielkie będą kiedyś jego zasługi w dziedzinie, która w jego czasach jeszcze nie istniała. Opracowaną przez siebie teorię związaną z szeregami wykorzystywał w badaniach nad przewodzeniem ciepła. Do Fouriera jeszcze wrócimy.
Definicje
Zanim przystąpimy do symulacji i pomiarów poznajmy definicje i znaczenia niektórych terminów. Zacznijmy od podstaw, czyli wyjaśnienia co to są harmoniczne. Załóżmy, że rozpatrujemy jakiś sygnał w dziedzinie częstotliwości. Jeśli w jego widmie występują składowe o całkowitych wielokrotnościach częstotliwości podstawowej, to nazywamy je harmonicznymi. Załóżmy, że analizujemy sygnał, w którym występują składowe np.: 100 Hz, 300 Hz i 500 Hz. Mówimy, że sygnał o częstotliwości podstawowej 100 Hz ma harmoniczne 300 Hz i 500 Hz, a więc są to harmoniczne: 3. i 5. Gdyby w widmie pojawiła się jakaś składowa o częstotliwości np. 217 Hz, to nie byłaby harmoniczną rozpatrywanego sygnału.
W kontekście harmonicznych często mówimy o zniekształceniach nieliniowych. Można więc odnieść wrażenie, że jest to parametr raczej niepożądany. Czy tak jest na pewno? Wróćmy do rozważań Fouriera. Doprowadziły one do wniosku, że każdy przebieg okresowy można złożyć z przebiegów sinusoidalnych o odpowiednio dobranych amplitudach i częstotliwościach harmonicznych. Naturalne jest więc, że sygnały prostokątne, piłokształtne czy większość innych występujących w naszym otoczeniu będą zawierały harmoniczne. Co więcej, gdyby ich nie miały, byłyby zniekształcone, gdyż ich istota polega właśnie na zawieraniu harmonicznych. W technice stosowany jest termin „sygnały odkształcone” określający przebiegi okresowe inne niż sinusoidalne. Zwróćmy uwagę na to, że nazywamy je odkształconymi, nie zniekształconymi. W pewnych sytuacjach, o których jeszcze będzie mowa, przebiegi odkształcone mogą ulec zniekształceniu, i wtedy zaczynają się prawdziwe problemy.
Bez harmonicznych nie istniałaby muzyka. Zaręczam, że słuchanie muzyki np. tworzonej przez syntezatory generujące dźwięki będące idealnymi sinusoidami na dłuższą metę byłoby nie do zniesienia. To właśnie harmoniczne nadają barwę dźwiękom, sprawiają że rozróżniamy poszczególne instrumenty i nasze własne głosy. To właśnie, jak twierdzą audiofile, parzyste harmoniczne wnoszone przez wzmacniacze lampowe decydują o ich miękkim i przyjemnym dla ucha brzmieniu. Zauważmy, że parzyste harmoniczne oznaczają wprowadzanie dźwięków przesuniętych o oktawę i jej wielokrotność w stosunku do dźwięku podstawowego. Z czysto muzycznego punktu widzenia dźwięki przesunięte o oktawę nie brzmią fałszywie, nie tworzą dysonansów. Może właśnie na tym polega magia wzmacniaczy lampowych.
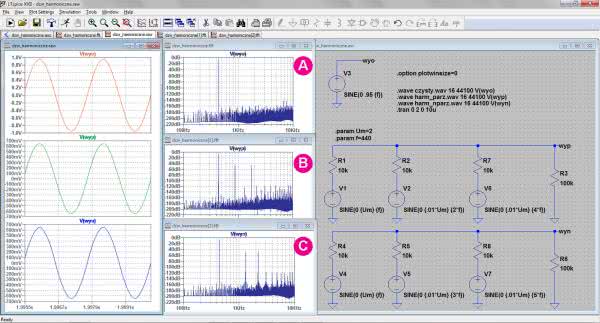
Aby przekonać się jak osobiście odczuwamy obecność harmonicznych w odsłuchiwanych dźwiękach wykonamy symulację, w której wygenerujemy ton a-razkreślne (440 Hz), do którego są strojone instrumenty w orkiestrach symfonicznych. Dodamy też dwa identyczne generatory, których dźwięki zostaną wzbogacone o dwie harmoniczne. W pierwszym przypadku będą to harmoniczne 2. i 4. o amplitudach równych 1% amplitudy dźwięku podstawowego, w drugim będą to harmoniczne 3. i 5. o takich samych amplitudach jak dla harmonicznych parzystych. Harmoniczne parzyste są sumowane z sygnałem podstawowym na rezystorze R3, a kompletny przebieg jest wyprowadzony na wyjście „wyp”. Dla harmonicznych nieparzystych są to odpowiednio rezystor R5 i wyjście „wyn”. Czysty przebieg jest dostępny na wyjściu „wyo” (rysunek 1).
W trakcie symulacji tworzone są pliki dźwiękowe: czysty.wav, harm_nparz.wav i harm_parz.wav, które można odsłuchać po zakończeniu symulacji. Pliki te wraz z plikiem symulacji (dzw_harmoniczne.asc) są dostępne w materiałach dodatkowych do artykułu.
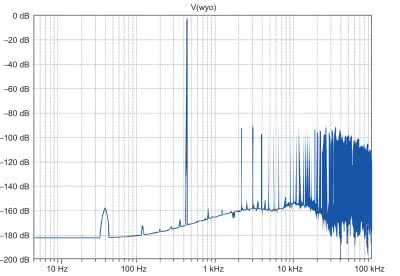
Do widocznych na rysunku w wykresów czasowych dodano wykresy FFT przedstawiające widmo każdego z trzech sygnałów. Wykres taki jest tworzony przez kliknięcie prawym przyciskiem myszki na danym wykresie czasowym i wybraniu opcji: View → FFT. Przyjmujemy parametry domyślne proponowane przez symulator. Uruchamiając symulację czasową .TRAN z jej domyślnymi parametrami może okazać się, że widmo będzie miało wysoko umieszczoną podłogę szumów, pojawią się w nim ponadto składniki, których raczej być nie powinno (rysunek 2).
Artefakty te powstają w wyniku algorytmów obliczania szybkiej transformaty Fouriera, liczby punktów branych do analizy, zastosowanych okien itp. Istnieje kilka środków poprawiających wynik analizy FFT. Pierwszym z nich jest skrócenie parametru Maximum Timestep instrukcji TRAN. Optymalną wartość tego parametru można ustalić metodą prób, pamiętajmy jednak, że wpływa on znacząco na całkowity czas symulacji. Drugim środkiem poprawiającym jakość wykresu FFT jest zablokowanie kompresowania punktów wyświetlanych w oknie FFT. W tym celu w dogodnym miejscu na schemacie należy umieścić komendę:
.option plotwinsize=0
Można jednak zastanawiać się jak daleko podobne optymalizacje mają sens? Czy na przykład potrafilibyśmy określić podłogę szumu w jakimś urządzeniu jeśli byłaby ona poniżej powiedzmy 120 dB, a nawet wyżej? Gdyby jednak z jakichś powodów zależało nam na uzyskaniu wyników o jak największej dokładności, można wykonać jeszcze jeden zabieg polegający na zwiększeniu precyzji obliczeń wykonywanych przez procesor komputera. Wpisując poniższą komendę uzyskujemy podwójną precyzję takich obliczeń:
.option numdgt=7
Na harmoniczne zupełnie inne spojrzenie mają energetycy, dla których stanowią one istny ból głowy. Jak wiemy, napięcie w naszych gniazdkach elektrycznych teoretycznie ma kształt sinusoidy. Osiągnięcie takiego ideału jest w większości przypadków praktycznie niemożliwe, ale zarówno dostawcy, jak i odbiorcy energii powinni podejmować działania ograniczające wprowadzanie do sieci zakłóceń ujawniających się jako harmoniczne 50 Hz. Mogą być one przyczyną zakłóceń pracy innych urządzeń elektrycznych, a nawet powodować ich uszkodzenia. Istnieją normy określające dopuszczalne poziomy poszczególnych harmonicznych do 40. włącznie.
Wróćmy jeszcze do definicji. Podstawowym parametrem określającym zawartość harmonicznych w sygnale jest współczynnik zawartości harmonicznych (zniekształceń nieliniowych). W praktyce spotykamy najczęściej jego angielską nazwę: Total Harmonic Distortion – THD. No i tu ujawniają się prawa Murphy’ego. Jedno z nich mówi, że jeśli gdzieś może wystąpić jakiś problem, to na pewno wystąpi. W tym przypadku problemem jest sama definicja. Jedna z nich określa współczynnik zawartości harmonicznych jako stosunek wartości skutecznych harmonicznych (bez częstotliwości podstawowej) do wszystkich składowych z częstotliwością podstawową włącznie. Tak definiowany współczynnik THD wyrażany jest zatem zależnością:
Często dla podkreślenia tak sformułowanej definicji, do oznaczenia THD dodawany jest indeks r. Inna definicja, spotykana znacznie częściej, odnosi stosunek wartości skutecznych samych harmonicznych (bez częstotliwości podstawowej) do składowej o częstotliwości podstawowej. Do tak zdefiniowanego współczynnika dopisywany jest zwykle indeks F:
(1)
Występujący w powyższych wyrażeniach parametr określający górną granicę sumowania jest równy nieskończoności, co jest zgodne z definicją, lecz trudne do spełnienia w praktyce, szczególnie w aplikacjach, w których parametr ten jest obliczany numerycznie. W programie LTspice THDF jest obliczany poleceniem:
.four <częstotliwość> [liczba_harmonicznych] [liczba_okresów] <węzeł_badany1> [<węzeł_badany3> ...]
Domyślna liczba harmonicznych jest równa 9. Jeśli chcemy uwzględnić ich więcej (lub mniej), parametr liczba_harmonicznych musi być podany.
Wrażenia subiektywne
Współczynnik zawartości harmonicznych jest parametrem często podawanym w danych technicznych urządzeń akustycznych, ale czy na pewno dobrze oddaje jakość urządzenia? Rozpatrzmy sygnał, w którym składowa o częstotliwości podstawowej ma amplitudę Um. Niech sygnał ten w pierwszym przypadku zawiera 2. harmoniczną o amplitudzie 5% Um i 7. harmoniczną o amplitudzie 10% Um. W następnym kroku zamienimy amplitudy: 2. harmoniczna będzie miała amplitudę 10% Um, a 7. harmoniczna 5% Um. Zawartość harmonicznych jest taka sama w obu przypadkach i równa ok. 11,2%. Wygenerujmy te sygnały w celu odsłuchania i porównania. Najpierw zrobimy to w symulatorze.
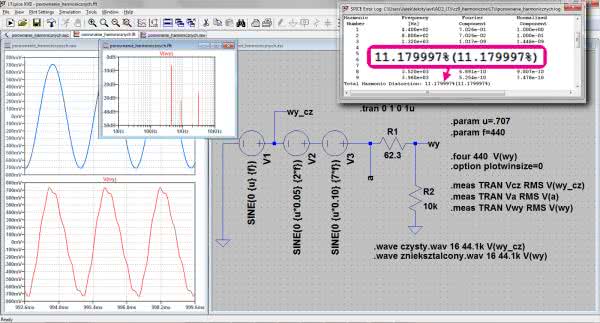
Na rysunku 3 pokazano schemat układu testowego. Źródło napięciowe V1 generuje składową podstawową o częstotliwości 440 Hz i amplitudzie 0,707 V. Harmoniczne są generowane przez źródła V2 (druga) i V3 (siódma). Sygnały akustyczne są tworzone znaną już instrukcją .WAVE. Zawsze generujemy ton o częstotliwości podstawowej, który jest dostępny na wyjściu „wy_cz”, natomiast sygnał z harmonicznymi występuje na wyjściu „wy”. Dzielnik napięciowy R1 i R2 dobrano tak, aby napięcie skuteczne sygnału zawierającego harmoniczne było takie samo jak sygnału bez harmonicznych. Poziomy napięć są mierzone instrukcjami .MEAS. Na wykresach czasowych przedstawiono przebieg oryginalny i zniekształcony, dodatkowo dodano wykres widma. Do zmierzenia współczynnika THD zastosowano instrukcję .FOUR. Jej wyniki oglądamy w oknie „SPICE Error Log” i jak widać są one zgodne z przewidywanymi teoretycznie, obliczonymi z zależności (1). W oknie wyników dostrzegamy jeszcze jedną wartość podaną w nawiasie. Jest to też parametr często podawany w specyfikacjach technicznych, w którym do wartości skutecznych wszystkich harmonicznych dodawane jest skuteczne napięcie szumów. Wszystko jest odnoszone do napięcia skutecznego częstotliwości podstawowej. Współczynnik ten jest oznaczany THD+N i jest opisany wzorem:
w którym Un jest skutecznym napięciem szumu w paśmie pomiaru (pamiętajmy, że szum zależy od pasma).
W wyniku symulacji na dysku zostają zapisane pliki czysty.wav i znieksztalcony.wav. Drugiemu z nich warto zmienić nazwę, np. na znieksztalcony_2_10___7_5.wav, co oznacza, że jest to przypadek dla amplitudy 2. harmonicznej równej 10% Um i 7. harmonicznej 5% Um.
Następnie we właściwościach źródeł V2 i V3 zmieniamy amplitudy odpowiednio na: {u*0,10} i {u*0,05) i powtarzamy symulację. Tym razem w pliku znieksztalcony.wav mamy sygnał z tak ustawionymi amplitudami. Współczynnik zawartości oczywiście się nie zmieni, czy nie zmienią się też subiektywne wrażenia odsłuchu? Pozostawiam do oceny Czytelnikom.
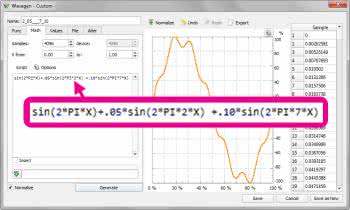
Podobną ocenę przeprowadzimy teraz odsłuchując sygnały generowane przez Analog Discovery 2. Użyjemy do tego pierwszego kanału generatora arbitralnego. Powstaje pytanie, jak zmusić urządzenie do tego, by generowało dokładnie takie same przebiegi jak w symulacji? W tym celu wybieramy tryb pracy generatora „Custom” i przystępujemy do definiowania własnego przebiegu naciskając ikonkę „New”. Otwiera się okno edytora przebiegu, w którym wybieramy zakładkę „Math”, co oznacza, że przebieg utworzymy opisując go wyrażeniem matematycznym (rysunek 4).
Wyrażenie to ma postać:
sin(2*PI*X) + .05*sin(2*PI*2*X) + .10*sin(2*PI*7*X)
Mamy w nim 3 składniki opisujące kolejno: składową podstawową, 2. harmoniczną i 7. harmoniczną. Tak opisany przebieg zostanie utworzony po naciśnięciu przycisku ekranowego Generate, w wyniku czego w oknie edytora pojawia się jego wykres. W polu „Name” wprowadzamy nazwę, np. 2_05___7_10 i zapisujemy w nowym pliku (Save_as_New). Analogicznie postępujmy z drugim przebiegiem, w którym zamieniamy wartości amplitud składowych harmonicznych. Po wygenerowaniu zapisujemy jako nowy pod nazwą np. 2_10___7_05. Podobnie możemy utworzyć czysty przebieg bez harmonicznych, albo użyć standardowego przebiegu sinusoidalnego o odpowiednio dobranych parametrach. Aby zachować zgodność z symulacją wybieramy częstotliwość 440 Hz i amplitudę 645 mV.
Wszystko jest już gotowe, możemy przystąpić do odsłuchu. Warto przy tym zapewnić sobie możliwość oglądania przebiegów na ekranie oscyloskopu. W tym celu wystarczy połączyć wyjście generatora (W1) z wejściem 1. kanału oscyloskopu (1+). Druga końcówka wejścia różnicowego (1–) powinna być dołączona do masy. Po upewnieniu się, że przebieg przypomina swym kształtem ten z symulacji korzystne będzie uruchomienie narzędzia Spectrum. Pozwoli ono dokładnie obejrzeć widmo sygnału oraz zmierzyć parametr THD (rysunek 5). Aby wykres widma był dobrze widoczny wybieramy parametr Frq Range=100 kHz to 122.1 Hz i zakres częstotliwości: Start=0, Stop=10 kHz. Współczynnik zawartości harmonicznych uzyskamy po wybraniu opcji: View → Measurements, a następnie Add → Trace1 → Dynamic → THD. Jak widać na rysunku 5 zmierzony parametr THD osiągnął wartość –19,03 dBc, gdy tymczasem LTspice podawał ją w procentach.
Do przeliczenia decybeli na procenty korzystamy z zależności:
(2)
THDF=–19,03 dBc odpowiada więc THDF=11,2%, co jest zgodne z symulacją. Przebiegi odsłuchujemy w słuchawkach dołączonych bezpośrednio do gniazda słuchawkowego Analog Discovery 2.
Istota powstawania harmonicznych
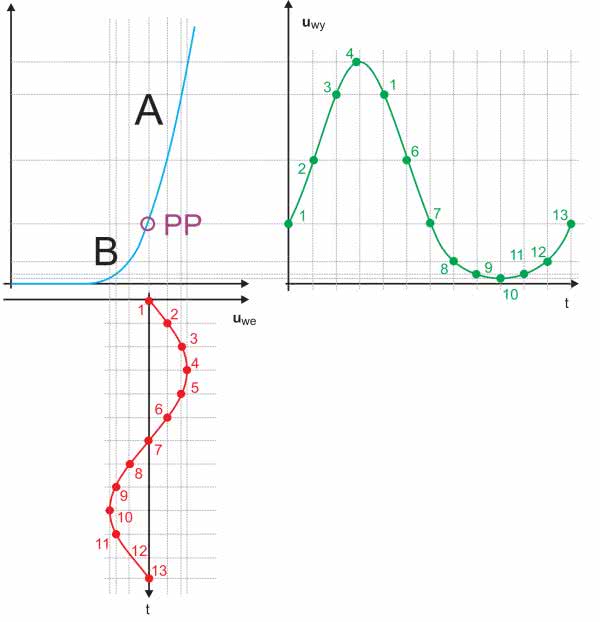
Zniekształcenia harmoniczne inaczej zwane nieliniowymi powstają w wyniku przetwarzania sygnału przez elementy o charakterystyce nieliniowej. Zasadę powstawania zniekształceń przedstawiono na rysunku 6.
Widzimy na nim charakterystykę elementu wzmacniającego (np. tranzystora lub lampy) z zaznaczono punktem pracy „PP”. Jest on ustawiony na pograniczu odcinka, który można w przybliżeniu uznać za liniowy (A) i kolana charakterystyki (B). Taki dobór punktu pracy powoduje, że wzmocniony sygnał wyjściowy (krzywa zielona) jest bardzo zniekształcony. Przedstawiony tu przypadek jest mocno przerysowany. Zabieg ten zastosowano, aby wyraźnie zilustrować mechanizm powstawania zniekształceń. Jak widać, górna połówka sinusoidy wzmacniana na liniowym odcinku charakterystyki pozostaje prawie niezniekształcona, dolna natomiast uległa znacznej deformacji. Przebieg wyjściowy nie jest więc już sinusoidą, a jedynie przebiegiem odkształconym. Z teorii Fouriera wiemy, że muszą pojawić się w nim harmoniczne.
Powyższy przykład ilustruje mechanizm powstawania zniekształceń nieliniowych. W tym miejscu można zadać pytanie, jaki jest sens podawania parametru THD np. dla wzmacniaczy akustycznych, skoro prawie nigdy nie wzmacniają czystych sygnałów sinusoidalnych. Trzeba jednak mieć na uwadze, że zniekształcenia nieliniowe powstają niezależnie od tego czy sygnałem wejściowym jest sinusoida czy dowolny inny przebieg – mechanizm pozostaje ten sam. Zatem skoro w efektem zniekształceń nieliniowych jest dodanie do sygnału harmonicznych, to te harmoniczne dodane do sygnału akustycznego zmienią subiektywne odbieranie barwy dźwięku.
Pozostając w tematyce akustycznej powstaje pytanie, jaki poziom zniekształceń harmonicznych jesteśmy w stanie tolerować, czyli traktować tak, że nie zmienia subiektywnie odczuwanej barwy dźwięku. Audiofile będą walczyć o każdy ułamek procenta, twierdząc że go słyszą, gdy tymczasem popularna niegdyś norma HiFi dopuszczała aż 1%. Obecnie produkowane wzmacniacze wyższej klasy osiągają THD rzędu 0,001%.
Przesterowanie
Jeżeli założylibyśmy, że odcinek A charakterystyki przedstawionej na rysunku 6 jest liniowy i przesunęlibyśmy punkt pracy PP nieco wyżej, to przy podaniu na wejście sygnału sinusoidalnego o niewielkim napięciu uzyskalibyśmy na wyjściu sygnał niezniekształcony, a więc nie zawierający harmonicznych. Istnieje jednak niebezpieczeństwo, że zwiększając napięcie wejściowe wejdziemy w strefę kolana charakterystyki (B), co jak już wiemy powoduje zniekształcenie sygnału wyjściowego i wzrost zawartości harmonicznych. Ale nawet gdy napięcie wejściowe mieści się w liniowym zakresie charakterystyki, to przy odpowiednio dużym wzmocnieniu wzmacniacza lub dużym napięciu wejściowym może dojść do jego przesterowania. Napięcie wyjściowe, które teoretycznie jest równe iloczynowi napięcia wejściowego i wzmocnienia nie może jednak rosnąć do nieskończoności. Barierę wyznacza napięcie zasilające. W stanie przesterowania górne lub dolne fragmenty sygnału (lub oba jednocześnie) są obcinane. Na oscyloskopie efekt ten będzie widoczny, ale harmoniczne zaczną szybko rosnąć zanim zauważymy obcinanie przebiegu. Czy jest jakaś metoda, która pozwoliłaby wykryć krytyczny moment, w którym harmoniczne zaczynają gwałtownie rosnąć? Okazuje się, że jest, i to niewiarygodnie wręcz skuteczna.
Rozważmy układ z rysunku 7. Jest to wzmacniacz odwracający o wzmocnieniu 10 V/V zasilany symetrycznym napięciem ±5 V. Teoretycznie, gdyby wzmacniacz był idealny, napięcie wyjściowe mogłoby osiągać wartość 10 Vpp (amplituda 5 V), co odpowiadałoby napięciu wejściowemu 1 Vpp.
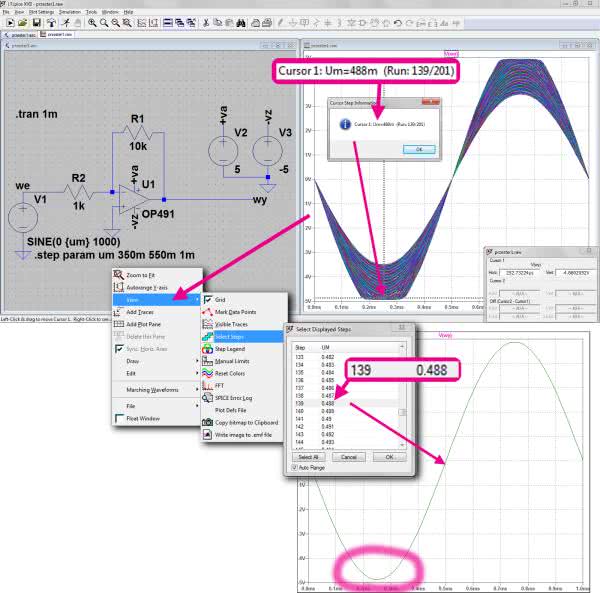
Zastosowany wzmacniacz OP491 jest typu rail-to-rail, jednak nawet dla takiego wzmacniacza potrzebny jest pewien margines napięcia od góry i od dołu. Sprawdźmy najpierw w przybliżeniu jakie maksymalne napięcie wejściowe można podać, aby nie przesterować wzmacniacza. Źródło sygnału wejściowego będzie generowało przebieg sinusoidalny o częstotliwości 1 kHz i amplitudzie {um} zadanej parametrycznie. Zakres zmian jest określony instrukcją:
.step param um 350m 550m 1m
co oznacza, że amplituda będzie się zmieniała od 350 mV do 550 mV co 1 mV. Pamiętajmy, że w symulatorze podajemy amplitudę, nie wartość międzyszczytową. Zastosujemy symulację .TRAN 1m, która obejmie dokładne jeden okres przebiegu. W celu określenia maksymalnej amplitudy wejściowej ustawiamy kursor na wykresie w pozycji minimum sygnału, naciskamy prawy przycisk myszki i używając kursorów „góra”, „dół” wybieramy ten przebieg, który wydaje się pierwszym zniekształconym. Nie jest to zadanie łatwe, a odpowiedź nie jest jednoznaczna i przesądzająca. Według mnie krytyczna amplituda to ok. 488 mV. Aby zobaczyć jak wygląda przebieg odpowiadający Uwe=488 mV możemy go wyodrębnić klikając prawym przyciskiem myszki na wykresie, a następnie wybrać opcje: View → Select Steps i z wyświetlonego zestawu zaznaczyć pozycję odpowiadającą 488 mV. Na wykresie pozostanie tylko jedna sinusoida, której można dokładniej się przyjrzeć. Dostrzegamy minimalne zniekształcenie dolnego fragmentu przebiegu, w samym minimum, ale jest ono bardzo subtelne.
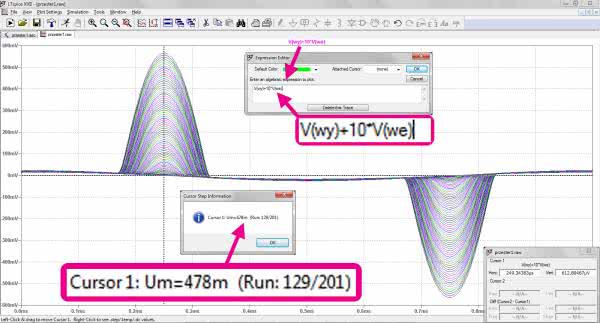
Znacznie dokładniejsze wskazanie otrzymamy, gdy po wcześniejszym przywróceniu wyświetlania wszystkich pozycji zmienimy wykres czasowy V(wy) na V(wy)+10·V(we). Wystarczy kliknąć prawym przyciskiem myszki na górny opis wykresu („V(wy)”) i wpisać powyższą formułę (rysunek 8).
W ten sposób uzyskujmy możliwość obserwowania różnicy między sygnałem wyjściowym a wzmocnionym sygnałem wejściowym. Znak „plus” zamiast minusa wynika z tego, że analizujmy wzmacniacz odwracający opisany zależnością:
Uwy=–Uwe·ku,
gdzie ku=–10 V/V.
W przypadku liniowej pracy wzmacniacza różnica ta powinna być stała, jednak już przy minimalnym przesterowaniu ujawniają się zmiany. Metoda diagnozowanie krytycznego napięcia wejściowego jest podobna jak w poprzednim przykładzie. Przyjmujemy zmiany napięcia wejściowego w zakresie od 350 mV do 550 mV z krokiem 1 mV i obserwujemy zależność V(wy)+10·V(we). Ustawiamy kursor np. w punkcie odpowiadającemu maksimum wykresu i za pomocą kursorów „góra”, „dół” znajdujemy ten krok, w którym uwidacznia się wyraźny skok wskazywanej wartości.
W naszym przykładzie można przyjąć, że sytuacja ta występuje dla Uwe=478 mV.
Sprawdźmy, jakim wartościom THD odpowiadają wykryte dwiema metodami stany wejścia w przesterowanie. Parametr THD jest obliczany w programie Ltspice funkcją .FOUR. Ważne jest zadbanie o jak największą dokładność obliczeń, co zapewni odpowiednią czystość widma.
W obliczeniach zwiększymy standardową liczbę harmonicznych analizowanych przez funkcję .FOUR z 9 do 15. Zadbamy ponadto o zwiększoną dokładność symulacji .TRAN nadając parametrowi „Maximum Timestep” wartość 1 ms. Pamiętajmy ponadto, że rozdzielczość szybkiej transformaty Fouriera zależy od analizowanego czasu. Minimalna odległość między prążkami widma FFT jest równa odwrotności tego czasu. Rozpatrujemy sygnał o częstotliwości 1 kHz. Jego harmoniczne są więc wielokrotnością tej częstotliwości, z czego wynikałoby, że minimalna rozdzielczość powinna być równa co najmniej 1 kHz, ale ponieważ chcielibyśmy również obejrzeć widmo decydujemy się na rozdzielczość 10 Hz. Wynika z tego, że czas symulacji powinien być równy 0,1 s. Ostatecznie do obliczeń wpisujemy instrukcje:
.TRAN 0 .1 0 0.1u
.OPTION plotwinsize=0
.FOUR 1k 15 V(wy)
.STEP PARAM um LIST 400m 478m 488m 600m
Podsumowując: czas analizy jest równy 0,1 s, parametr „Maximum Timestep”=0,1 ms, wyłączona kompresja danych, analiza sygnału o częstotliwości 1 kHz obserwowanego na wyjściu układu. Uwzględniamy 4 przebiegi o amplitudach 400 mV, 478 mV, 488 mV i 500 mV. Sygnał 400-miliwoltowy powinien być czysty, gdyż mieści się w liniowym zakresie pracy wzmacniacza, sygnał 478 mV to ten, który uznaliśmy jako graniczny w drugiej, bardziej precyzyjnej metodzie. Sygnał 488 mV wybraliśmy jako graniczny na podstawie obserwacji wykresu czasowego, natomiast sygnał o amplitudzie 600 mV powinien już czysto teoretycznie przesterować wzmacniacz. Zwiększyliśmy ponadto liczbę analizowanych harmonicznych do 15. Przyjęte opcje powodują znaczne spowolnienie pracy symulatora, ale jest to cena za uzyskanie dużej dokładności obliczeń.
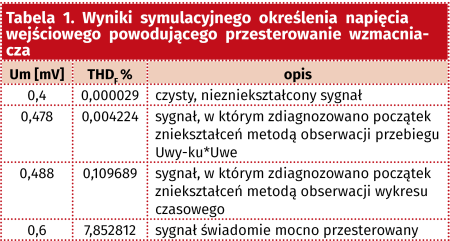
Wyniki zestawiono w tabeli 1, natomiast na rysunku 9 pokazano kształt przebiegów i ich widma.
Z pomiarów wynika, że ocena zniekształceń na podstawie wzrokowej obserwacji kształtu przebiegu pozwoliła na wychwycenie zawartości harmonicznych na poziomie ok. 0,1%, ale taki wynik uzyskano porównując jednocześnie przebiegi zniekształcony i czysty. Metoda oceny przesterowania przez obserwację wyniku wyrażenia Uwy-ku*Uwe (w rozpatrywanym przypadku ku=–10 V/V) wykazała niespodziewanie wysoką dokładność. W tym przypadku stan wejścia w przesterowanie zdiagnozowano przy zawartości harmonicznych rzędu 0,004% (sic!). Ale to jeszcze nie wszystko. Istnieje jeszcze jedna metoda pozwalająca określić maksymalne napięcie wejściowe zapewniające liniową pracę wzmacniacza. Jest to charakterystyka przejściowa: Uwy=f(Uwe), która w programie LTspice jest ukryta pod analizą DC sweep. Jako parametry należy wskazać źródło sygnału wejściowego oraz podać typ zmian napięcia (liniowe, dekadowe, oktawowe, wyszczególniane), zakres zmian „Start value”, „Stop value” i krok zmian „Increment”. Po uruchomieniu symulacji należy wskazać punkt pomiarowy (np. V(wy)). Symulator wykreśla charakterystykę przejściową Uwy=f(Uwe), którą podobnie jak w poprzednich symulacjach można zmodyfikować na (Uwy-ku·Uwe)=f(Uwe). Ustalenie punktu załamania charakterystyki przejściowej odznacza się wówczas dużą precyzją, szczególnie po powiększeniu zakresu obejmującego tylko punkty załamania. Taki pomiar pokazano na rysunku 10.
Pomiary układu rzeczywistego
Po sporej dawce pracy z symulatorem LTspice nadszedł moment weryfikacji pomiarów wirtualnych. Sprawdzimy, jak będzie zachowywał się dokładnie taki sam układ elektroniczny zbudowany z elementów rzeczywistych. Źródłem sygnału wejściowego będzie 1. kanał generatora arbitralnego Analog Discovery 2. Układ zasilamy napięciami +5 V i –5 V. Kanał 1. oscyloskopu dołączamy do wejścia, w tym samym punkcie, w którym dołączony jest generator, kanał 2. dołączamy do wyjścia układu. W generatorze wybieramy przebieg sinusoidalny o częstotliwości 1 kHz i regulowanej amplitudzie. Zakres regulacji ograniczamy do 400...600 mV.
Najpierw obserwujemy przebiegi na oscyloskopie. Aby były dobrze widoczne ustawiamy czułość kanału 2. na 1,1 V/dz, podstawę czasu na 100 ms/dz, dla której będzie widoczny tylko jeden okres przebiegu. Pozwoli to dokładne przyglądać się jego szczegółom. Zmieniając napięcie generatora w całym zakresie upewniamy się, że wzmacniacz wchodzi w stan przesterowania. Podobnie jak w symulacji określenie tego momentu tylko na podstawie obserwacji oscylogramu nie jest zbyt precyzyjne.
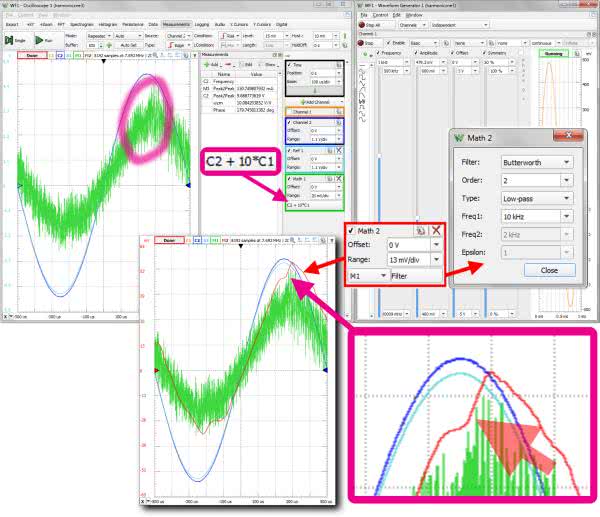
Przed przystąpieniem do dalszych działań warto zapisać oscylogram z kanału 2. jako przebieg referencyjny w stanie, gdy wzmacniacz pracuje jeszcze liniowo, np. dla Uwe=460 mV. Klikamy prawym przyciskiem myszki w polu pod opisem kanałów i z sekcji „Reference” wybieramy „Channel 2”. Aktualny przebieg z kanału 2. zostanie zamrożony na ekranie pod nazwą „Ref 1”. W kolejnym kroku tworzymy kanał użytkownika: klikamy prawym przyciskiem myszki pod opisem kanałów, a następnie wybieramy opcje: Custom → Math. Po kliknięciu w pole definiujące kanał („Math 1”) otwiera się okno, w którym możemy zapisać formułę matematyczną dla tego kanału. Wpisujemy analogiczną formułę, jakiej używaliśmy w symulatorze, a więc: C2+10·C1
Na ekranie oscyloskopu pojawi się przebieg wyznaczający różnicę między sygnałem wyjściowym wzmacniacza a wzmocnionym sygnałem wejściowym (rysunek 11). Przypominam, że wzmacniacz ma wzmocnienie 10 i pracuje w konfiguracji odwracającej, stąd znak plus w wyrażeniu.
Przebieg z kanału „Math 1” wygląda jak zaszumiona sinusoida, ale mimo tego jest dość dobrym wskaźnikiem wejścia w stan przesterowania.
Wskaźnik ten można jeszcze ulepszyć kojarząc z kanałem „Math 1” kolejny kanał filtrujący. Znowu klikamy prawym przyciskiem myszki w pole pod opisem kanałów i z sekcji „Math” wybieramy „Filter”. Następnie ustawiamy parametry filtru:
Filter=Butterworth, Order=2, Tupe=Low-pass, Freq1=10 kHz
Nie zapomnijmy wskazać sygnału filtrowanego. Będzie nim oczywiście „M1”, a więc sygnał z kanału „Math 1”. Teraz już bardzo dobrze widoczny jest artefakt ujawniający się w stanie przesterowania.
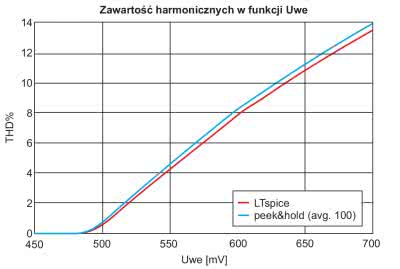
Do pomiaru zniekształceń nieliniowych (zawartości harmonicznych) układu rzeczywistego użyjemy wirtualnego analizatora widma zestawu Analog Discovery 2 – Spectrum. Stanowi on rozwinięcie funkcji FFT dostępnej w oscyloskopie. Przyrząd jest obsługiwany na wzór prawdziwych analizatorów widma, ale dla nas najważniejszą jego cechą jest zestaw funkcji pomiarowych, które zwykle nie występują w funkcji FFT oscyloskopu. Jedną z nich jest THD, a więc dokładnie to, czego poszukujemy. Trzeba jednak mieć świadomość tego, że Spectrum ma dynamikę ograniczoną do ok. 80 dB, więc pod tym względem dość znacznie ustępuje prawdziwym analizatorom. Mimo ograniczeń pomiar zawartości harmonicznych wykazał dość dobrą zbieżność z wynikami uzyskanymi w symulatorze. O ile lokalizacja wejścia w stan przesterowania wypadła niemal identycznie w symulacji i w pomiarach, o tyle krzywa THD zmierzonego przez Spectrum Analog Discovery 2 jest dla dużych Uwe zaniżona z powodu ograniczenia pomiaru widma do 100 kHz. Zwiększenie szerokości pasma skutkowałoby niestety zmniejszeniem rozdzielczości i gubieniem harmonicznych, co w efekcie dyskwalifikowałoby taki pomiar. Porównanie wyników pokazano na rysunku 12.
Analizator pracował w trybie Peak Hold z uśrednianiem 100 pomiarów. Opcję tę wybiera się z okna parametrów „Trace 2”, należy też wprowadzić parametr Count=100. Pomiar THD jest możliwy po wykonaniu sekwencji poleceń:
View → Measurements → Add → Trace2 → Dynamic → THD
Wyniki są podawane w jednostkach dBc. Do przeliczenia na procenty korzystamy z zależności (2).
Wnioski
Metoda detekcji wejścia w stan przesterowania wykorzystująca obserwację zależności Uwy-ku*Uwe sprawdza się, dopóki przesunięcie fazowe między Uwe i Uwy jest niewielkie. Dla dużych przesunięć znika charakterystyczny artefakt, a różnica między Uwy a ku*Uwe ma w dużym zakresie zmian Uwe kształt sinusoidy, która odkształca się w chwili wyjścia z liniowej pracy wzmacniacza. Dla względnie dużych częstotliwości zaobserwujemy nagły wzrost zawartości harmonicznych na długo przed wejściem w stan nasycenia wzmacniacza. Przebieg wyjściowy nie jest obcinany, zaczyna natomiast przybierać kształt piły, co oczywiście jest równoznaczne ze wzrostem zawartości harmonicznych.
W następnym odcinku zbudujemy charakterograf.
Jarosław Doliński, EP

 Zaloguj
Zaloguj