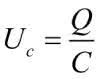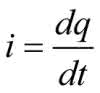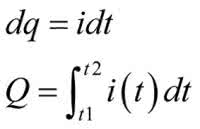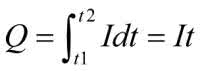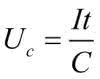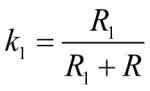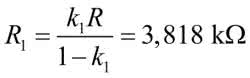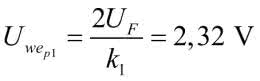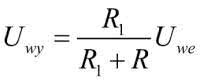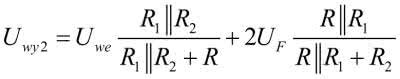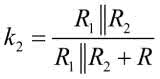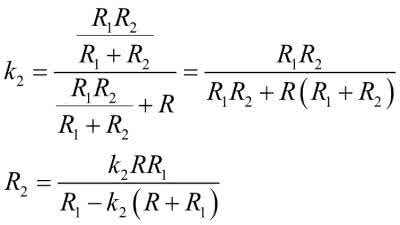Warunek generacji – parametr, który jak wynika z jego definicji, musi być spełniony do wzbudzenia drgań. To sprzymierzeniec elektronika konstruktora, ale też jego wróg. Jakże często zdarza się, że gdy chcemy, by jakiś układ generował, ma on problemy ze wzbudzeniem się i odwrotnie, wzmacniacze bardzo chętnie wchodzą w stan oscylacji. Chociaż wykorzystanie warunku generacji to bardzo dobra metoda uzyskania czystej, niezniekształconej sinusoidy, nie będziemy podążać tą drogą. Generatory można konstruować również w oparciu na zupełnie innych zasadach. Naszym celem w tym odcinku będzie dążenie do uzyskania jak najczystszego sygnału sinusoidalnego. Sprawdzimy, która z metod da zadowalające wyniki. Nie zawsze generowanie sinusoidy jest procesem czysto analogowym.
Metoda I
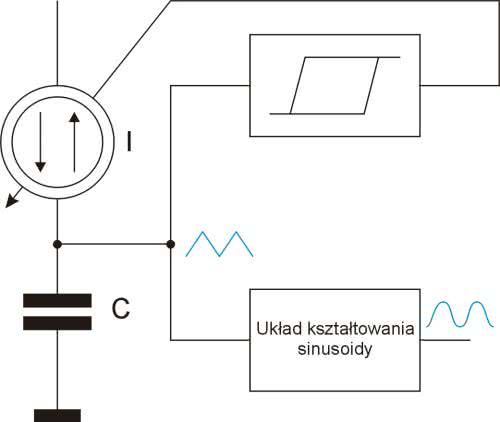
Wyobraźmy sobie generator zbudowany na zasadzie zilustrowanej na rysunku 1.
Mamy tu źródło prądowe, w którym może być zmieniane natężenie prądu oraz jego kierunek. Prąd tego źródła w zależności od kierunku ładuje lub rozładowuje kondensator C. Napięcie na kondensatorze jest równe:
ale ładunek można powiązać z prądem zależnością:
stąd
Jeśli zapewnimy stałoprądowe ładowanie (i rozładowanie) kondensatora, to:
gdzie t jest czasem ładowania kondensatora od t1 do t2.
Zatem napięcie na kondensatorze jest opisane zależnością:
i jak widać, jest to zależność liniowa. Szybkość ładowania kondensatora o pojemności C zależy tylko od prądu.
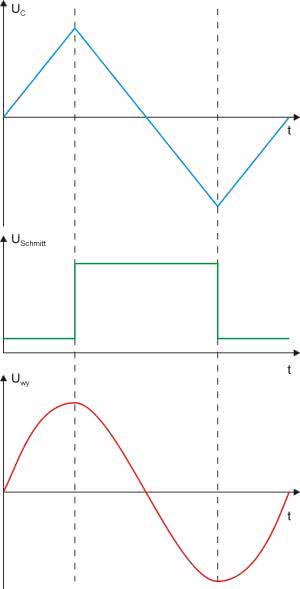
Liniowo narastające napięcie kondensatora jest podawane na wejście przerzutnika Schmitta. Przyjmiemy, że jego wyjście po włączeniu zasilania jest w stanie niskim, co powoduje przepływ prądu w kierunku ładującym kondensator C. Po osiągnięciu górnego napięcia progowego następuje zmiana stanu wyjścia przerzutnika, wywołując tym samym zmianę kierunku przepływu prądu ze źródła. Od tego momentu kondensator jest stałoprądowo rozładowywany, a więc napięcie na nim maleje liniowo. Po przekroczeniu dolnego napięcia progowego ponownie następuje przerzut i zmiana kierunku przepływu prądu. Wracamy zatem do punktu wyjścia i jak widać, układ będzie generował napięcie trójkątne występujące na kondensatorze. Częstotliwość przebiegu zależy wyłącznie od prądu płynącego przez kondensator. Generator jest więc przestrajany poprzez zmianę wydajności źródła prądowego. Przebiegi w charakterystycznych punktach układu pokazano na rysunku 2. Nie będziemy się teraz szczegółowo zajmować poszczególnymi blokami takiego generatora. Mają one elementarną i dość prostą budowę.
Kompletując je w całość, otrzymalibyśmy gotowe urządzenie.
W sposób bardziej lub mniej zamierzony zbudowaliśmy generator funkcyjny. Generuje on na pewno dwa podstawowe przebiegi, tj. trójkąt i prostokąt, nad trzecim (sinusoidalnym) trzeba będzie jeszcze trochę popracować.
Można oczywiście wymyślić metodę filtrowania przebiegu prostokątnego. Wykorzystalibyśmy w niej fakt, że jest złożeniem wielu nieparzystych harmonicznych, teoretycznie nieskończonej ich liczby. Amplitudy maleją odwrotnie proporcjonalnie do numeru danej harmonicznej. Metoda stosunkowo prosta i warta sprawdzenia, jak jest skuteczna, co uczynimy w dalszej części artykułu. Ma jednak jedną podstawową, w zasadzie dyskwalifikującą wadę – konieczność stosowania przestrajanego filtru. Nie jest to nie do zrobienia, ale drastycznie komplikuje budowę urządzenia. Widzimy natomiast, że przebieg trójkątny bardzo przypomina sinusoidę. A gdyby tak obciąć go od góry i od dołu?
No nie. Raczej nie idźmy tą drogą, chociaż znane są aplikacje, w których takie podejście jest stosowane. Użytkownicy samochodów lubiący jeździć na biwaki w rejony nieucywilizowane prawdopodobnie mieli do czynienia z przetwornicami stałego napięcia akumulatorowego na napięcie zmienne stanowiące substytut napięcia sieciowego 230 V. W większości takich urządzeń generowane jest napięcie trapezoidalne zamiast sinusoidalnego i jak widać, podejście to sprawdza się w praktyce. Zobaczmy, jak bardzo przebieg trapezoidalny odbiega od sinusoidalnego. Zastosujemy oczywiście metodę symulacji. Wygenerujemy trzy przebiegi: trójkątny i dwa trapezoidalne. Aby sprawdzić, jak bardzo różnią się od czystej sinusoidy, zmierzymy zawartość harmonicznych. Sprawdzimy, jak na zwartość harmonicznych wpłynie poziom obcięcia wyjściowego przebiegu trójkątnego.
Do wygenerowania przebiegów zastosujemy źródło napięciowe PWL z nieudokumentowaną opcją REPEAT FOREVER. Definicja dla przebiegu trójkątnego jest następująca:
PWL repeat forever(0 0 200u 8 +400u -8 +200u 0)endrepeat
W powyższym zapisie kolejne pary liczb oznaczają czas i odpowiadające mu napięcie sygnału. Możliwy jest zapis bezwzględnych lub przyrostowych wartości czasu. W drugim przypadku odniesieniem jest poprzedni punkt zapisu. Jeśli definicja ma dotyczyć przebiegu okresowego, wystarczy utworzyć ujęte w nawias punkty opisujące jeden pełny okres, a poza nawiasami dopisać opcje FOREVER i ENDREPEAT. Definicje przebiegów trapezoidalnych są następujące:
PWL repeat forever(0 0 150u 6 +100u 6 +300u -6 +100u -6 +150u 0)endrepeat
PWL repeat forever(0 0 +100u 4 +200u 4 +200u -4 +200u -4 +100u 0)endrepeat
Przebieg ma okres 800 μs, a więc jego częstotliwość jest równa 1250 Hz. Do analizy harmonicznych zastosujemy funkcję .four. Konieczne jest wprowadzenie 3 komend, niezależnie dla każdego wyjścia:
.four 1250 11 v(wy1)
.four 1250 11 v(wy2)
.four 1250 11 v(wy3)
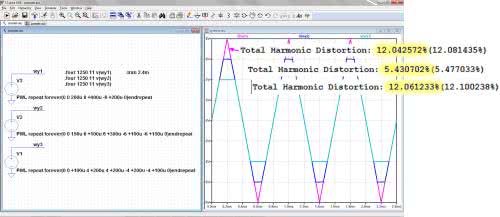
W komendzie podana jest częstotliwość podstawowa (1250 Hz) oraz liczba analizowanych harmonicznych włącznie z pierwszą. Wyniki pokazano na rysunku 3.
Współczynnik zawartości harmonicznych odczytujemy komendą „View→SPICE Error Log” powodującą wyświetlenie okna z interesującymi nas informacjami. Odczytujemy z nich, że:
- dla przebiegu trójkątnego THD=12,04%,
- dla przebiegu z wyjścia „wy2” THD=5,43%,
- dla przebiegu z wyjścia „wy3” THD=12,06%.
Jak widać, dla odpowiednio dobranego poziomu przycięcia przebiegu trójkątnego można uzyskać zawartość harmonicznych na poziomie kilku procent. O ile w pewnych zastosowaniach technicznych jest to wartość do zaakceptowania, o tyle gdybyśmy chcieli użyć takiego generatora jako przyrządu pomiarowego, byłaby to całkowita klapa. Czy można więc coś z tym zrobić?
Okazuje się, że można, choćby przez zastosowanie diodowych układów kształtujących. Zaprojektujemy teraz taki układ, sprawdzimy go w symulacji, a następnie w praktyce.
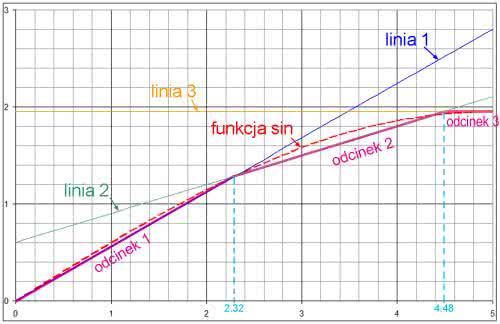
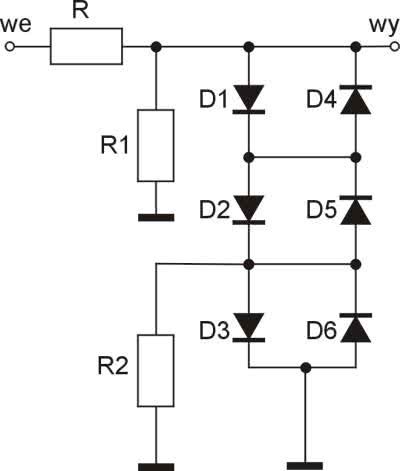
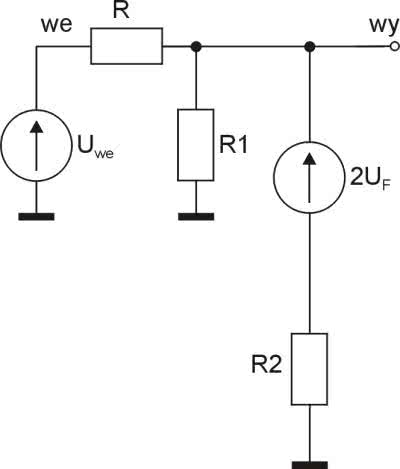
Ze względu na symetrię sinusoidy wystarczy nam analiza tylko jednej ćwiartki: od 0 do p/2. Zakładamy, że przebieg trójkątny, z którego tworzymy sinusoidę ma amplitudę 5 V. Przyjmujemy również, że sinusoida będzie aproksymowana 3 odcinkami, tak jak to pokazano na rysunku 4. Dokładny (matematyczny) przebieg jest na nim zaznaczony kolorem czerwonym. Wyboru nachylenia poszczególnych odcinków oraz punktów przegięcia dokonujemy arbitralnie, wpasowując je ręcznie na wykresie. Należy podkreślić, że pracujemy na charakterystyce przejściowej, a więc zależności napięcia wyjściowego od wejściowego. Schemat ideowy układu pokazano na rysunku 5.
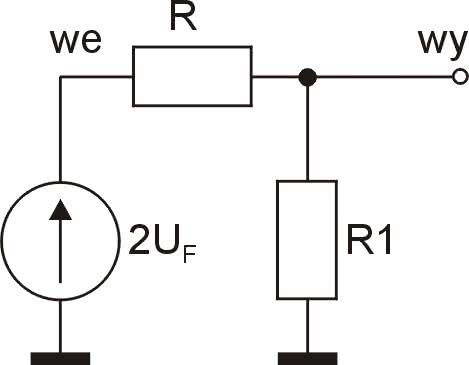
Dla małych napięć wejściowych wszystkie diody są wyłączone. W układzie istotne są tylko rezystory R i R1 (rysunek 6). Z rysunku 4 wynika, że pierwszy odcinek powinien mieć nachylenie k1=0,56 V/V. Taka więc powinna być transmitancja dzielnika R, R1.
Przyjmując rezystancję R równą 3 kΩ, obliczamy R1:
Po przekształceniach:
Pierwsze wejściowe napięcie progowe jest równe:
gdzie UF napięcie przewodzenia diody równe 0,65 V.
Odcinek 1. pokrywa się z linią 1:
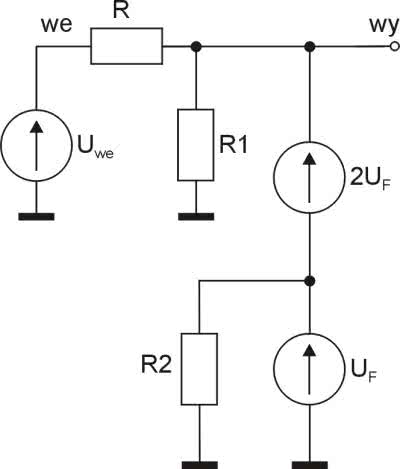
Zwiększając napięcie wejściowe, dochodzimy do momentu, w którym zaczynają przewodzić diody D1 i D2 (D4 i D5 dla napięć ujemnych). Dioda D3 jest bocznikowana rezystorem R2, więc aby weszła w stan przewodzenia, wymagane jest wyższe napięcie wejściowego. Przewodzące diody można traktować jak źródła napięciowe o napięciu UF. Schemat zastępczy dla tego przypadku jest pokazany na rysunku 7.
Dla lepszej czytelności uwzględniono tylko elementy dla dodatnich napięć wejściowych. Ponieważ w obwodzie występują dwa źródła napięciowe, do obliczenia napięcia wyjściowego korzystamy z zasady superpozycji. Ostatecznie jest ono równe:
Jak widać, napięcie to zmieniło na charakterystyce nachylenie i dodatkowo uległo przesunięciu. Obowiązujący w tym stanie współczynnik kierunkowy dla linii 2 jest równy:
Z wykresu szacujemy ten współczynnik dla 2. odcinka na 0,3. Przekształcamy więc powyższe wyrażenie tak, aby obliczyć z niego R2:
Stąd po podstawieniu wartości otrzymujemy R2=1938 Ω.
Dalsze zwiększanie napięcia wejściowego spowoduje włączenie diody D3. Od tego momentu obowiązuje schemat zastępczy pokazany na rysunku 8. Wynika z niego, że powyżej napięcia progowego Uwep2 napięcie wyjściowe jest równe 3UF=1,95 V. Odpowiadające mu napięcie wejściowe obliczamy z zależności (1), podstawiając do niego: Uwy2=1,95 V i obliczone wartości rezystorów. Otrzymujemy Uwep2=4,48 V.
Wszystko już jest obliczone, możemy przystąpić do symulacji. Najpierw sprawdzimy, jak obliczona charakterystyka przejściowa wygląda w układzie z elementami fizycznymi. Musimy pamiętać, że w obliczeniach jako model diody przyjmowaliśmy idealne źródło napięciowe włączane skokowo po przekroczeniu określonego napięcia progowego. Tymczasem prawdziwa dioda jest włączana stopniowo, a jej napięcie przewodzenia zmienia się też w pewnym zakresie w miarę zwiększania prądu. Symulacja obejmie 3 obwody obowiązujące w rozważnych w obliczeniach zakresach napięcia wejściowego, a także jeden model układu fizycznego. Schemat układu symulowanego wraz z wynikami pokazano na rysunku 9. W modelu układu fizycznego zastosowano dostępne w bibliotece LTspice’a krzemowe diody przełączające BAV170HM. Plik symulacji ch_ka_przejsciowa.asc jest dostępny w materiałach uzupełniających do artykułu.
Symulacja pokazała, że uzyskano całkiem niezłą zgodność modelu obliczeniowego z modelem zawierającym elementy fizyczne. Jedynie w zakresie powyżej 2. punktu progowego charakterystyka układu z elementami fizycznymi w widocznym stopniu odbiegała od modelu obliczeniowego. Ciekawe, jak zachowa się układ rzeczywisty w pomiarze?
Symulacja działania diodowego układu kształtującego
Układ mamy już zaprojektowany, przyszła więc kolej na sprawdzenie, jaka będzie jego odpowiedź na wejściowy przebieg trójkątny o amplitudzie 5 V (zgodnie z założeniami obliczeń). Najpierw, tak jak zwykle, poddamy go symulacji. Schemat układu kształtującego wraz z wynikami symulacji pokazano na rysunku 10.
Źródło sygnału wejściowego jest zdefiniowane jak niżej:
PULSE({-um} {um} 0 .5m .5m 0 1m)
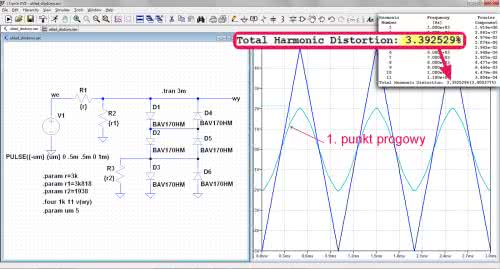
Amplitudę określono parametrycznie, aby możliwe było łatwe badanie jej wpływu na przebieg wyjściowy. Domyślnie jest opisana jako: .param um 5, a więc ma wartość 5 V. Wejściowy przebieg trójkątny ma czas narastania 0,5 ms i czas opadania 0,5 ms. Okres tego przebiegu jest równy 1 ms, co odpowiada częstotliwości 1 kHz. Przebieg wyjściowy ma kształt zbliżony do sinusoidy, ale można dość wyraźnie zaobserwować 1. punkt progowy odpowiadający napięciu wejściowemu nieco ponad 2 V.
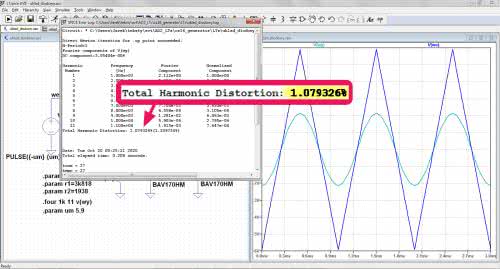
W symulacji uwzględniono pomiar zawartości harmonicznych, tak jak robiliśmy to wcześniej, tylko teraz częstotliwość jest równa 1 kHz. Okazało się, że zawartość harmonicznych przebiegu wyjściowego jest równa 3,39%. Hm. Rewelacji nie ma. Wcześniej zwróciliśmy uwagę na to, że charakterystyka przejściowa układu kształtującego przebiegała wyraźnie powyżej charakterystyki obliczeniowej, spróbujmy zatem podwyższyć nieco amplitudę wejściową, np. do 5,9 V (rysunek 11). Teraz przebieg wygląda znacznie lepiej, co znajduje również odzwierciedlenie w zawartości harmonicznych. THD jest równe 1,08%, a to już można uznać za wynik całkiem niezły. Pora na pomiary układu rzeczywistego.
Pomiar diodowego układu kształtującego sinusoidę
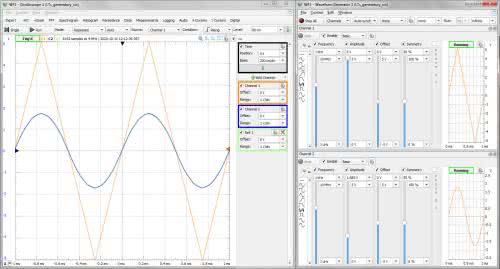
Rzeczywisty układ budujemy dokładnie według schematu z symulacji. W testowanym układzie znalazły się wyciągnięte z głębokiego lamusa diody BAVP17 (może BAVP19). Źródłem wejściowego przebiegu trójkątnego jest 1. kanał generatora arbitralnego. Ustawiamy amplitudę 5 V i częstotliwość 1 kHz. Rezystory R1 i R2 w układzie pomiarowym zostały zastąpione potencjometrami wieloobrotowymi, na których ustawiono wartości wynikające z obliczeń. Uruchamiamy generator i oscyloskop. Wyniki pokazano na rysunku 12. Dla lepszej weryfikacji wzrokowej przebiegu wyjściowego, kanał 1. oscyloskopu został na chwilę dołączony do 2. kanału generatora arbitralnego generującego sinusoidę wzorcową. Oscylogram sinusoidy wzorcowej zapisujemy jako przebieg referencyjny. Amplitudę sygnału generatora dobrano tak, aby obie sinusoidy – wzorcowa i wytwarzana w układzie kształtującym – pokryły się ze sobą. Porównanie wizualne wypada nieźle. Widać jednak, że sinusoida układu kształtującego nie osiąga przewidzianej w obliczeniach amplitudy 1,95 V.
Dokładniejsza ocena jakości przebiegu wymaga pomiaru współczynnika zniekształceń harmonicznych. Jest to możliwe za pomocą narzędzia Spectrum Analyzer zestawu Analog Discovery 2. Otwieramy go i ustawiamy parametry pomiaru: Top=10 dBV, Bottom=–109 dBV, aktywny pomiar Trace 2 – Channel C2, Freq. Range=100 kHz to 122.1 Hz, Start=0 Hz, Stop=100 kHz, Scale=Linear. Uaktywniamy ponadto pomiar Trace2→Dynamic→THD.
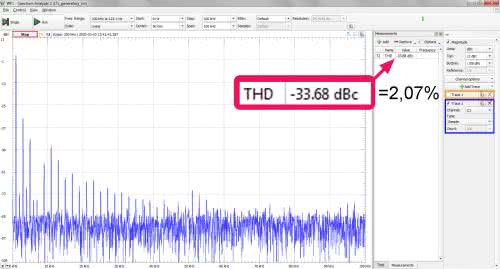
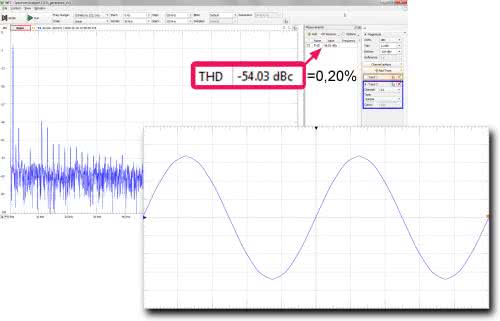
Wynik pomiaru pokazano na rysunku 13. Zawartość harmonicznych jest podawana w jednostkach dBc. Do przeliczenia na procenty korzystamy z zależności:
Jest to wynik lepszy niż w symulacji, ale spróbujemy go jeszcze poprawić. W tym celu uruchamiamy analizator w trybie ciągłym tak, aby kręcąc pokrętłami potencjometrów, można było obserwować na bieżąco skutek tego działania. Kręcimy w kierunku, w którym zniekształcenia się zmniejszają. Po przekroczeniu minimum delikatnie wracamy do niego, a następnie tę samą czynność wykonujemy regulując potencjometrem R2. Niestety, w trakcie korzystania z analizatora widma nie ma możliwości podglądania przebiegu na oscyloskopie Analog Discovery 2. Jeśli chcemy to robić, trzeba skorzystać z jakiegoś zewnętrznego przyrządu. Tą metodą udało się osiągnąć zniekształcenia harmoniczne na poziomie ok. 0,2%, a taki wynik należy już uznać za bardzo dobry (rysunek 14).
Metoda II
Wrócimy jeszcze do metody generowania przebiegu sinusoidalnego polegającej na filtracji harmonicznych przebiegu prostokątnego. Chociaż należy uznać, że ma ona mało cech praktycznych, to na pewno jest interesująca z dydaktycznego punktu widzenia. W praktyce może być stosowana np. wtedy, gdy wymagany jest jeden przebieg sinusoidalny o określonej i stałej częstotliwości. Wydaje się, że dużo łatwiejsze jest wygenerowanie przebiegu prostokątnego i poddanie go filtracji niż generowanie czystego przebiegu sinusoidalnego dobrej jakości.
Podejście do metody II może być dwojakie. W pierwszym stosujemy filtr selektywny przepuszczający tylko jedną częstotliwość. Filtr jest nastrojony na częstotliwość przebiegu prostokątnego i właśnie taka sinusoida pojawia się na wyjściu. Niedogodnością tej metody jest trudność w zbudowaniu selektywnego filtru przepuszczającego jedną częstotliwość. Popularny mostek typu podwójne T jest filtrem zaporowym. Aby uzyskać filtr przepustowy, konieczne jest umieszczenie go w pętli sprzężenia zwrotnego, a więc dodanie czynnego elementu, który może wnosić własne zniekształcenia harmoniczne. Druga metoda, która wiąże się również z dodaniem filtru aktywnego, polega na zastosowaniu filtru górnozaporowego tłumiącego wszystkie częstotliwości powyżej częstotliwości podstawowej. Aby był on wystarczająco skuteczny, powinien być co najmniej 2. rzędu.
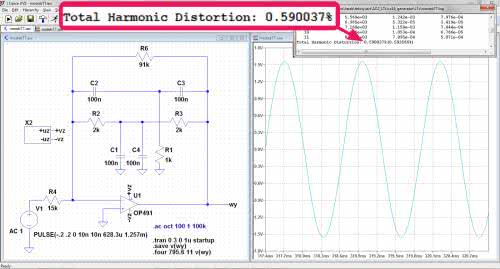
Zobaczmy, jaki wynik uzyskamy z filtrem podwójne T? Aby nie komplikować obliczeń, nie będziemy go stroić do wybranej częstotliwości, tylko zbudujemy z dostępnych w szufladzie elementów i obliczymy, jaka będzie dla nich częstotliwość tłumienia. Schemat układu pokazano na rysunku 15, a symulacja jest dostępna w pliku mostekTT.asc. Do budowy filtru zastosowano elementy R=2 kΩ i C=100 nF. Częstotliwość środkowa jest więc równa:
Okres i półokres przebiegu prostokątnego o tej częstotliwości są równe odpowiednio: T=1,257 ms i T/2=628,3 μs. Zgodnie z tym źródło sygnału wejściowego zdefiniowano w symulatorze jako:
PULSE(-.2 .2 0 10n 10n 628.3u 1.257m)
Dla podwyższenia dokładności obliczeń symulacji Transient określono parametr Timestep. Została mu nadana wartość 1 μs. Parametr ten może znacznie wydłużyć czas obliczeń, aby go skrócić do maksimum, zastosowano komendę SAVE v(wy). Powoduje ona tablicowanie wyników tylko z węzła „wy”, ale pozostałe węzły nas nie interesują w tej symulacji i można je pominąć.
Należy zauważyć, że mostek TT jest zbocznikowany rezystorem 91 kΩ, który zabezpiecza przed pracą wzmacniacza operacyjnego z otwartą pętlą sprzężenia zwrotnego. Wizualnie przebieg wyjściowy jest bardzo porządny. Obliczona komendą .four 795.8 11 v(wy) zawartość harmonicznych wyniosła 0,59%. Jest to zdecydowanie mniej niż w symulacji diodowego układu kształtującego, ale pamiętamy, że tamten w wersji rzeczywistej udało się podstroić tak, że harmoniczne spadły do 0,2%. Sprawdźmy, jakie parametry będzie miał rzeczywisty układ z filtrem podwójne T.
Pomiar układu z filtrem TT
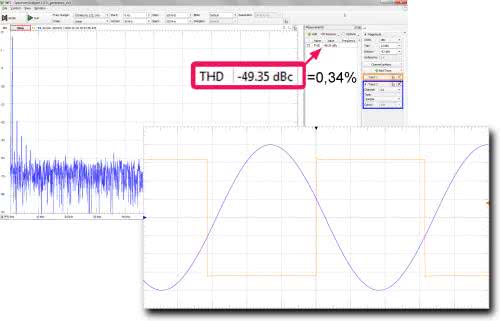
Metoda pomiaru jest dokładnie taka sama jak poprzednio. Zmieniamy tylko rodzaj przebiegu wejściowego z piłokształtnego na prostokątny. Pierwsze pomiary wykazały konieczność zmniejszenia amplitudy przebiegu prostokątnego tak, aby nie przesterować wzmacniacza operacyjnego. Do pomiaru harmonicznych, tak jak poprzednio użyliśmy analizatora widma zestawu Analog Discovery 2. Jak się okazało, zniekształcenia harmoniczne uzyskanej sinusoidy są równe –49,35 dBc, czyli 0,34% (rysunek 16), a więc lepiej niż w symulacji, ale gorzej niż z układem kształtowania sinusoidy. Jest to wynik trochę zaskakujący. Należy sądzić, że decyduje o tym zastosowany w filtrze wzmacniacz operacyjny.
W artykule znalazło się miejsce na omówienie dwóch metod generowania przebiegu sinusoidalnego, co oczywiście nie wyczerpało tematu. Może powrócimy do niego w następnym odcinku.
Jarosław Doliński, EP

 Zaloguj
Zaloguj