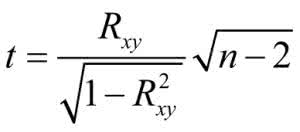Mamy świadomość zjawiska starzenia się komponentów elektronicznych mając na myśli przede wszystkim kondensatory elektrolityczne, lecz ten proces dotyczy także innych komponentów, takich jak rezystory, diody, itd. By dowiedzieć się jaki wpływ na wartość rezystancji rezystorów ma ich czas życia, przeprowadzono obliczenia, wsparte testami laboratoryjnymi. Do analizy zastosowano metodę starzenia komponentów poprzez ich przechowywanie w ustalonych temperaturach przez ustalony czas.
Serię rezystorów poddano symulacji w komorze termicznej, odpowiadającej pracy elementów przez 10 latach. Do obliczenia warunków symulacji zastosowano szereg obliczeń i założeń. Profil temperatury jest obliczany dla symulacji 2 zmian temperatury dziennie, w przeciągu 10 lat.
Analiza obejmuje samonagrzewanie części i możliwy wzrost temperatury poszczególnych elementów – zakłada się, że temperatura oporników jest utrzymywana w najgorszych warunkach.
Obliczony cykl temperaturowy został zbudowany na podstawie modelu Coffina-Mansona oraz modelu Arrheniusa. Na podstawie tych modeli obliczono, że test zawiera 183 cykle, czyli musi trwać blisko 23 dni nieprzerwanie. Każdy cykl jest podzielony na dwa stany: niski i wysoki. Niski cykl trwa 35 minut w temperaturze –40°C, a cykl wysoki trwa 146 minut w 140°C. Testowi poddano partię 1000 sztuk rezystorów o wartości 10 kΩ firmy PANASONIC z serii ERJ3EKF, 1%, obudowa SMD0603. Zestaw testowy został zaprezentowany na fotografii otwierającej. Test został przeprowadzony na specjalnie zaprojektowanych płytkach PCB, które pozwalały na pomiar rezystancji, tak jak pokazano na rysunku 1.
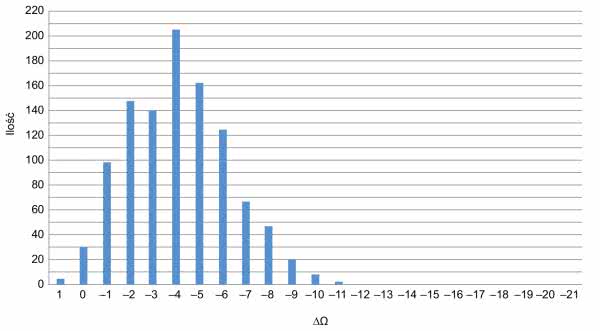
Po symulacji w komorze termicznej przeprowadzono analizę statystyczną. Obliczono, że 96,8% badanych elementów zwiększyła wartość rezystancji. Rozkład liczby zmian rezystancji w funkcji wielkości zmian rezystancji przedstawia rysunek 2.
Uzyskane wyniki średnie i trendy wskazują, że zmiana rezystancji rezystorów jest zauważalna, ale bardzo nieznaczna (tabela 1).
Przeprowadzono dalsze obliczenia, aby lepiej ocenić to zjawisko. Zbadano znaczenie liniowej jednowymiarowej funkcji regresji. Zastosowano do tego obliczone wcześniej średnie i odchylenia standardowe, a następnie obliczono moment korelacji zmiennych z próby oraz jego współczynnik korelacji liniowej. Współczynnik korelacji liniowej charakteryzuje stopień zależności liniowej między zmiennymi losowymi. Gdy współczynnik wynosi –1 lub 1, istnieje ścisła liniowa zależność między zmiennymi losowymi. Gdy współczynnik wynosi 0, zmienne są nieskorelowane. Im bliżej 1, tym silniejsza korelacja. W analizowanym przypadku współczynnik korelacji wynosi 0,95, co oznacza, że korelacja zmian rezystancji funkcji czasu jest bardzo silna.
Do dalszej analizy obliczamy:
Stosując rozkład t-Studenta dla ∞ ilości stopni swobody i α=0,01, znajdujemy t_α=2,576. Współczynnik t dla analizowanego przypadku wynosi 67,94.
Jeżeli uzyskany wynik jest większy lub równy t_α, oznacza to, że hipotezę o braku korelacji między analizowanymi zmiennymi należy odrzucić.
Piotr Ptak

 Zaloguj
Zaloguj