Mnożenie to działanie, którego implementacja z samych tablic LUT jest dość złożona. Z drugiej strony, jest bardzo popularna przy cyfrowym przetwarzaniu sygnałów. Zauważyli to także producenci układów FPGA i postanowili rozwiązać ten problem poprzez dodanie sprzętowych bloków, realizujących funkcje mnożenia. W dokumentacji spotyka się je pod różnymi nazwami. W produktach Intela bardziej zaawansowane bloki noszą nazwę DSP (DSP blocks). W rodzinie MAX10 zaimplementowana została uproszczona wersja, nazwana po prostu „mnożarką” (embedded multiplier), której opis znajdziemy na [2].
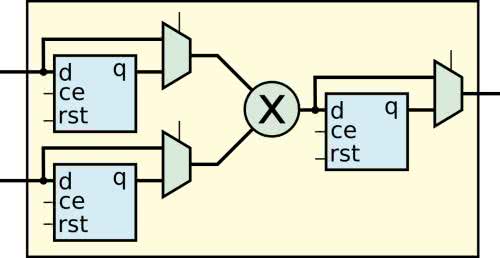
Uproszczony schemat mnożarki pokazuje rysunek 1. Mamy tam dwa wejścia przyjmujące wektory bitów, interpretowane jako czynniki. Mogą one, ale nie muszą, zostać zatrzaśnięte we wbudowanym rejestrze. Jego zastosowanie pozwala na uzyskanie wyższej częstotliwości pracy. Następnie mamy logikę kombinacyjną, realizującą mnożenie. Iloczyn, podobnie jak czynniki, może zostać zatrzaśnięty w rejestrze wyjściowym. Dodatkowo, dla każdego wejścia można skonfigurować liczbę w formie ze znakiem albo bez znaku.
Pojedyncza mnożarka może wykonywać pojedyncze mnożenie liczb 18-bitowych albo dwa mnożenia liczb 9-bitowych. Do przechowywania wyniku mnożenia dwóch czynników, zapisanych odpowiednio na N1 i N2 bitach, potrzebnych jest N1+N2 bitów. Łatwo możemy policzyć, że uzyskane wyniki będą miały odpowiednio 36 albo 18 bitów długości. Mnożarki mogą być użyte dla czynników mniejszej długości. Niewykorzystane bity zostaną wypełnione bitem znaku.
W układach z rodziny MAX10, w zależności od wersji, może być od 16 do 144 niezależnych mnożarek. Płytka Rysino wyposażona jest w FPGA 10M04, który zawiera ich 20.
Mnożenie liczb zespolonych
Aby zademonstrować sposób użycia nowo poznanych bloków, zaimplementujemy mnożenie zespolone. Zaczniemy więc od bardzo krótkiej powtórki z algebry. Mamy dwie liczby zespolone a i b, które rozpiszemy jako:
a=are+jaim
b=bre+jbim
gdzie are i bre odpowiadają części rzeczywistej, a aim i bim części urojonej; j symbolizuje jednostkę urojoną, czyli pierwiastek z –1. Jeśli rozpiszemy mnożenie, otrzymamy:
ab=(are+jaim)(bre+jbim)=arebre+jareaim+jaimbre–aimbim=(arebre–aimbim)+j(areaim+aimbre)
Mnożenie dwóch liczb zespolonych możemy zatem zrealizować jako cztery mnożenia i dwa dodawania. Istnieją wprawdzie sprytne sposoby zmniejszenia liczby mnożeń do 3, lecz pozostaniemy przy bardziej klasycznym sposobie [3].
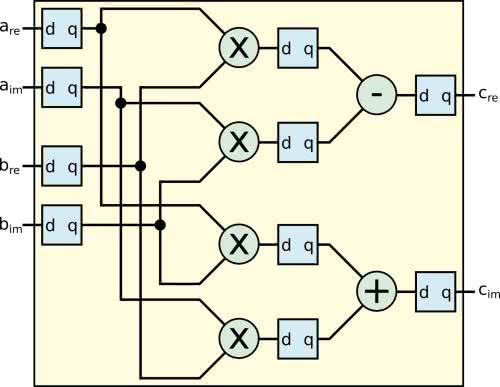
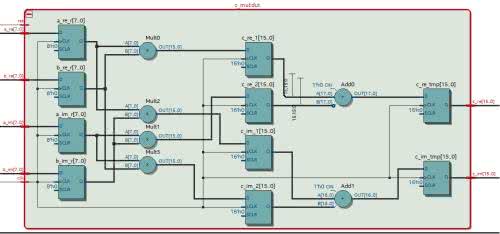
Na rysunku 2 pokazano sposób implementacji uzyskanego przez nas wzoru w układzie FPGA. Moduł przyjmuje cztery wektory wejściowe. Najpierw są one zatrzaskiwane w rejestrach. W drugim takcie następuje równoległe wykonanie czterech mnożeń rzeczywistych. Uzyskane wyniki są zatrzaskiwane w kolejnych rejestrach. W trzecim takcie następuje wykonanie dodawania i odejmowania. Wynik jest zapisywany w rejestrach wyjściowych. Tak przygotowany moduł będzie miał latencję trzech taktów zegara.
Kod realizujący mnożenie liczb zespolonych pokazuje listing 1. Stworzony moduł nosi nazwę c_mul. W liniach 11…13 zdefiniowane są trzy parametry. K definiuje długość wektora danych wejściowych. K_OUT1 i K_OUT2 decydują, które z bitów końcowego wyniku mają znaleźć się na wyjściu. Dalej (linie 15…22) znajdują się wejścia i wyjścia. Ponieważ chcemy, aby działania zostały wykonane na liczbach ze znakiem, przy definicji wektorów używamy słowa kluczowego signed.
10 module c_mul #(
11 parameter K = 9,
12 parameter K_OUT1 = 8,
13 parameter K_OUT2 = 16
14 ) (
15 input wire clk,
16 input wire rst,
17 input wire signed [K-1:0]a_re,
18 input wire signed [K-1:0]a_im,
19 input wire signed [K-1:0]b_re,
20 input wire signed [K-1:0]b_im,
21 output logic signed [K_OUT2-K_OUT1:0]c_re,
22 output logic signed [K_OUT2-K_OUT1:0]c_im
23 );
24 logic signed [K-1:0]a_re_r;
25 logic signed [K-1:0]a_im_r;
26 logic signed [K-1:0]b_re_r;
27 logic signed [K-1:0]b_im_r;
28
29 logic signed [2*K-1:0] c_re_1;
30 logic signed [2*K-1:0] c_re_2;
31 logic signed [2*K-1:0] c_im_1;
32 logic signed [2*K-1:0] c_im_2;
33
34 logic signed [2*K:0] c_re_tmp;
35 logic signed [2*K:0] c_im_tmp;
36
37 always_ff @(posedge clk) begin
38 a_re_r <= a_re;
39 a_im_r <= a_im;
40 b_re_r <= b_re;
41 b_im_r <= b_im;
42 end
43
44 always_ff @(posedge clk) begin
45 c_re_1 <= a_re_r * b_re_r;
46 c_re_2 <= a_im_r * b_im_r;
47 c_im_1 <= a_re_r * b_im_r;
48 c_im_2 <= a_im_r * b_re_r;
49 end
50
51 always_ff @(posedge clk) begin
52 c_re_tmp <= c_re_1 – c_re_2;
53 c_im_tmp <= c_im_1 + c_im_2;
54 end
55
56 assign c_re = c_re_tmp[K_OUT2:K_OUT1];
57 assign c_im = c_im_tmp[K_OUT2:K_OUT1];
58 endmodule
Kolejną częścią jest definicja zmiennych pomocniczych. Tutaj także używamy słowa kluczowego signed. Pierwsze cztery (linie 24…27) będą tworzyły rejestry zatrzaskujące wejścia. Ich długość jest więc równa K. Kolejne cztery będą przechowywały wyniki poszczególnych mnożeń, stąd ich długość musi być odpowiednio większa i wynosi 2K. Na końcu (34…35) znajdują się rejestry wyjściowe. Zarówno dodawanie, jak i odejmowanie wymaga wydłużenia o jeden dodatkowy bit, stąd otrzymujemy wektory o długościach 2K+1.
Teraz możemy przejść do implementacji samej logiki modułu. Składają się na nią trzy bloki always_ff. Pierwszy (37…42) odpowiada za zatrzaskiwanie danych wejściowych. Najciekawszą funkcję realizuje kolejny blok (44…49), gdzie następuje mnożenie. Jest ono realizowane po prostu poprzez użycie operatora *, podobnie jak w wielu innych językach. Dopiero przy budowaniu projektu środowisko Quartus wykryje, że to działanie może zostać wykonane w specjalnym bloku i wyinferuje mnożarkę. Możemy także, poprzez dodanie odpowiednich ustawień, wymusić, aby zamiast wykorzystania specjalnych modułów, mnożenie zostało złożone ze zwykłych elementów logicznych.
W ostatnim bloku always_ff realizowanie jest dodawanie i odejmowanie. Na samym końcu (linie 56…57) następuje wycięcie zadanych bitów wyniku. Za pomocą polecenia assign są one przypisane do wyjść modułu.
Testujemy
Do sprawdzenia działania naszego modułu wykorzystamy testbench, którego najciekawsze fragmenty pokazane są na listingu 2. Najpierw definiujemy pomocnicze stałe (linie 12…14). K to długość wektorów reprezentujących dane wejściowe, LATENCY to latencja, a TESTS to liczba działań, które chcemy wykonać w ramach testów. Następnie (wiersze 23…26) tworzymy cztery pomocnicze tablice, o długości równej latencji modułu. Wykorzystamy je do przechowywania danych wejściowych i porównania ich z danymi wyjściowymi, otrzymanymi po ich propagacji przez moduł.
11 module c_mul_tb;
12 parameter K = 9;
13 parameter LATENCY = 3;
14 parameter TESTS = 10;
23 int ra_re[LATENCY-1:0];
24 int ra_im[LATENCY-1:0];
25 int rb_re[LATENCY-1:0];
26 int rb_im[LATENCY-1:0];
39 initial begin
40 int rc_re, rc_im;
41 @(posedge clk);
42 @(posedge clk);
43 @(posedge clk);
44 for (int i = 0; i < TESTS+LATENCY; i++) begin
45 @(negedge clk);
46 if (i >= LATENCY) begin
47 rc_re = ra_re[i%LATENCY]*rb_re[i%LATENCY]-ra_im[i%LATENCY]*rb_im[i%LATENCY];
48 rc_im = ra_re[i%LATENCY]*rb_im[i%LATENCY]+ra_im[i%LATENCY]*rb_re[i%LATENCY];
49 $display("sim: %d+%dj rtl: %d+%dj",
50 rc_re, rc_im, c_re, c_im);
51 end
52 rb_re[i%LATENCY] = 100;
53 rb_im[i%LATENCY] = 50;
54 ra_re[i%LATENCY] = i*511.0/(TESTS-1)-256;
55 ra_im[i%LATENCY] = 255-i*511.0/(TESTS-1);
56
57 a_re = ra_re[i%LATENCY];
58 a_im = ra_im[i%LATENCY];
59 b_re = rb_re[i%LATENCY];
60 b_im = rb_im[i%LATENCY];
61 @(posedge clk);
62 end
63 $stop;
64 end
Generowanie przypadków testowych znajdziemy w pętli for. Jeden obieg pętli odpowiada jednemu przypadkowi testowemu. Dodatkowe obiegi odpowiadające latencji pozwalają nam poczekać na ostatnie wyniki. Aktualne wymuszenia są generowane w liniach 52…55 i zapisywane w tablicach pod adresem i%LATENCY. Zostaną odczytane przez kod z wierszy 47…50, po upływie LATENCY cyklów, a następnie wykorzystane do wyznaczenia oczekiwanego wyniku i wyświetlone razem z wyjściem z modułu.
Symulację możemy uruchomić, przechodząc w programie ModelSim do folderu 12_mul i po wywołaniu rozkazu: do c_mul.do
Po zakończeniu symulacji w konsoli pojawią się oczekiwane oraz uzyskane wyniki. Tak jak widzimy na listingu 3, najpierw pojawia się wynik z symulacji (oczekiwany), a potem z kodu rtl. W naszym przypadku są one zgodne. Uzyskane przebiegi czasowe pokazuje rysunek 3. W liniach 3…6 widzimy dane wejściowe. Na trzecim narastającym zboczu zegara, po pojawieniu się przebiegów, na wyjściu widać odpowiadający im wynik.
# sim: -38350+ 12700j rtl: -38350+ 12700j
# sim: -29800+ 9850j rtl: -29800+ 9850j
# sim: -21250+ 7000j rtl: -21250+ 7000j
# sim: -12850+ 4200j rtl: -12850+ 4200j
# sim: -4300+ 1350j rtl: -4300+ 1350j
# sim: 4250+ -1500j rtl: 4250+ -1500j
# sim: 12800+ -4350j rtl: 12800+ -4350j
# sim: 21200+ -7150j rtl: 21200+ -7150j
# sim: 29750+ -10000j rtl: 29750+ -10000j
# sim: 38300+ -12850j rtl: 38300+ -12850j
Dodajemy UART
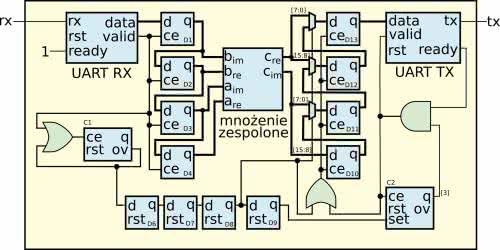
Aby przetestować nasz nowy moduł, w sprzęcie musimy jeszcze dodać moduł, odpowiedzialny za dostarczanie danych wejściowych i odbieranie wyjścia. Do komunikacji wykorzystamy port szeregowy. Schemat przygotowanego modułu pokazuje rysunek 4. Aby uprościć odbieranie danych, liczby wejściowe są 8-bitowe ze znakiem. Na rysunku, dla uproszczenia, pominięty został sygnał zegarowy – należy pamiętać, że wszystkie przerzutniki są taktowane z jednego zegara. Niektóre bloki mają także wyprowadzone złącze reset. Wszystkie one są połączone razem i resetowane jednym sygnałem.
Dane odbierane są przez znany nam już moduł odbiornika. Następnie trafiają na rejestr przesuwny, złożony z przerzutników D1…D4. Przez port po kolei przesyłamy część rzeczywistą i urojoną, najpierw dla czynnika a, później b. Dzięki temu, po wysłaniu wszystkich czterech wartości, znajdą się w rejestrach podłączonych do odpowiednich wejść modułu. Równocześnie dla każdej odebranej danej następuje inkrementacja licznika C1. Zlicza on modulo 5. Kiedy odebrane zostaną wszystkie cztery dane, na jego wyjściu OV pojawi się stan 1, który utrzyma się dokładnie przez jeden takt zegara. Będzie się on propagował przez linię opóźniającą, złożoną z przerzutników D6, D7 i D8. Dzięki temu płynie on razem z obliczeniami w module c_mux. Dlatego, gdy na wyjściu pojawi się wynik, multipleksery spowodują, że zostanie on przekazany na wejście rejestrów D10…13 i zapisany do nich. Uzyskany wynik ma długość dwa razy po 17 bitów. Aby zmieścić się w 4 bajtach, najstarsze bity nie będą przesyłane. W kolejnym takcie zegara rejestr D9 zostanie ustawiony i wpisze do licznika C2 liczbę 4, czyli 100 (w zapisie binarnym). Rozpocznie to proces wysyłania danych i multipleksery przestawią się w konfiguracji rejestru przesuwnego. Kiedy wszystkie dane zostaną przekazane, licznik C2 „przekręci się”, co spowoduje wyzerowanie bitu q[3] i zakończenie transmisji. Najpierw wysłana będzie część rzeczywista, później część urojona wyniku. Kolejność wysyłania to tak zwane littleendian. Oznacza to, że najpierw zostanie wysłanych 8 mniej znaczących, a później 8 bardziej znaczących bitów.
Implementacja logiki z rysunku 4 znajduje się na listingu 4. W wierszach 10…17 widzimy definicję modułu. Ma on trzy wejścia: zegarowe, reset i rx oraz jedno wyjście tx. Deklaracje wewnętrznych połączeń zostały pominięte – można je znaleźć w całym pliku dostępnym w repozytorium. Dalej w liniach 31…34 znajduje się instancja odbiornika portu szeregowego. Jej wyjście wchodzi na 4-elementowy rejestr przesuwny (wiersze 36…42). Na rysunku 4 składa się on z przerzutników D1…D4. Następnie znajdziemy moduł licznika modulo 5, który zlicza bajty odebrane przez port szeregowy. W liniach 51…59 jest nasz moduł mnożenia liczb zespolonych. Dalej w wierszach 61…65 widzimy rejestr przesuwny, opóźniający sygnał odebrania danych o latencję mnożenia (przerzutniki D6…D9). Kolejny blok always_ff (67…73) to wyjściowy rejestr przesuwny z zewnętrznym ładowaniem. Multipleksery zostały zrealizowane za pomocą operatora ?:. W liniach 81…87 znajduje się 3-bitowy licznik danych wyjściowych. Tym razem nie wykorzystaliśmy naszego starego modułu counter, ponieważ potrzebne nam było dodatkowe wejście, wpisujące do licznika liczbę 4. Na samym końcu znajdziemy instancję nadajnika portu szeregowego.
10 module uart_mul #(
11 parameter F = 8000000
12 ) (
13 input wire clk,
14 input wire rst,
15 input wire rx,
16 output logic tx
17 );
31 assign bus_rx.ready = 1’b1;
32 uart_rx #(.F(F), .BAUD(BAUD)) urx (
33 .rx(rx),
34 .bus(bus_rx));
35
36 always_ff @(posedge clk)
37 if (bus_rx.valid) begin
38 data_in[0] <= bus_rx.data;
39 data_in[1] <= data_in[0];
40 data_in[2] <= data_in[1];
41 data_in[3] <= data_in[2];
42 end
43
44 counter #(.N(5)) cnt_in (
45 .clk(clk),
46 .rst(rst),
47 .ce(bus_rx.valid | cnt_in_ov),
48 .q(),
49 .ov(cnt_in_ov));
50
51 c_mul #(.K(8), .K_OUT1(0), .K_OUT2(15)) dut (
52 .clk(clk),
53 .rst(rst),
54 .a_re(data_in[3]),
55 .a_im(data_in[2]),
56 .b_re(data_in[1]),
57 .b_im(data_in[0]),
58 .c_re(c[0]),
59 .c_im(c[1]));
60
61 always_ff @(posedge clk or negedge bus_rx.rst)
62 if (!bus_rx.rst)
63 valid_d <= ‘0;
64 else
65 valid_d <= {valid_d[2:0], cnt_in_ov};
66
67 always_ff @(posedge clk)
68 if (select_out | valid_out) begin
69 data_out[0] <= c[1][15:8];
70 data_out[1] <= select_out ? c[1][7:0] : data_out[0];
71 data_out[2] <= select_out ? c[0][15:8] : data_out[1];
72 data_out[3] <= select_out ? c[0][7:0] : data_out[2];
73 end
74
75 assign bus_tx.valid = valid_out;
76 assign bus_tx.data = data_out[3];
77
78 assign valid_out = cnt_out[2] & bus_tx.ready;
79 assign select_out = valid_d[2];
80
81 always_ff @(posedge clk or negedge bus_rx.rst)
82 if (!bus_rx.rst)
83 cnt_out <= 3’b000;
84 else if (valid_d[3])
85 cnt_out <= 3’b100;
86 else if (valid_out)
87 cnt_out <= cnt_out + 3’b1;
88
89 uart_tx #(.F(F), .BAUD(115200)) utx (
90 .bus(bus_tx),
91 .tx(tx));
Fragmenty kodu służącego do symulacji znajdziemy na listingu 5. W wierszu 15 widzimy listę bajtów, które zostaną wysłane. Odpowiadają one dwóm przypadkom testowym. Pierwszy z nich to mnożenie (4+8j)(2+5j), którego oczekiwanym wynikiem jest –32+36j. Drugi to (2+4j)(5+10j)=–30+40j. Do generowania sygnału testowego oraz odbierania wyniku wykorzystane są dodatkowe instancje nadajnika i odbiornika portu szeregowego. Samo wysyłanie odbywa się w pętli przedstawionej w wierszach 31…40. Po przesłaniu wszystkich danych odczekujemy jeszcze 400 ms. Po tym czasie symulacja zostanie zakończona.
15 logic [7:0]data[7:0] = {8’d10, 8’d5, 8’d4, 8’d2, 8’d5, 8’d2, 8’d8, 8’d4};
27 initial begin
28 bus_tx.valid = 1’b0;
29 #5000;
30
31 for (int i = 0; i < $size(data); i++) begin
32 @(negedge clk);
33 bus_tx.data = data[i];
34 bus_tx.valid = 1’b1;
35 @(posedge clk);
36 @(posedge clk);
37 bus_tx.valid = 1’b0;
38 while (!bus_tx.ready)
39 @(posedge clk);
40 end
41
42 #400us;
43 $stop;
44 end
Symulację uruchamiamy poleceniem:
do uart_mul.do
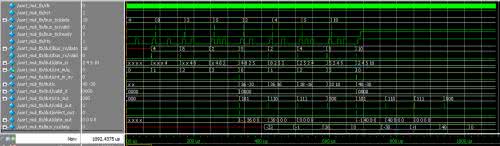
Uzyskany wynik pokazuje rysunek 5. W trzecim wierszu widzimy wchodzące dane. Kolejna linia to sygnał valid wyzwalający ich przesyłanie. Samą komunikację możemy zaobserwować w wierszu szóstym. Linia siódma to kolejne bajty odbierane przez port szeregowy. Wiersz dziewiąty (data_in) pokazuje aktualny stan wejściowego rejestru przesuwnego. Kolejny sygnał (q) to licznik wejściowy. Ciekawe informacje możemy także wyczytać z linii 12 – jest to wyjście z mnożenia. Widzimy, że nowe wyniki pojawiają się co takt zegara i bazują na kolejnych wartościach z wejściowego rejestru przesuwnego. Jednak zatrzaśnięte i wysłane z powrotem będą tylko wartości uzyskane dla poprawnego stanu wejść.
Zwracane dane widzimy w ostatnim wierszu. Dla pierwszego mnożenia otrzymujemy –32, –1, 36, 0. Gdy zapiszemy te liczby w bitach, otrzymamy: 1110 0000, 1111 1111, 0010 1000, 0000 0000. Ponieważ najpierw przesyłamy mniej znaczący bajt, po złożeniu otrzymamy liczby: 1111 1111 1110 0000 i 0000 0000 0010 1000. Po zamianie na system dziesiętny, zgodnie z oczekiwaniami otrzymamy –32+36j. Wynik drugiego mnożenia możemy odczytać analogicznie.
Sprzęt
Mamy już gotowy projekt. Ostatnim etapem będzie budowa w środowisku Quartus i testy w sprzęcie. Przy okazji zobaczymy, w jaki sposób zostanie zinterpretowane mnożenie. Otwieramy więc projekt 12_mul/mul.qpf i rozpoczynamy jego budowę. Kiedy się zakończy, możemy w panelu Tasks wybrać opcję: Compile Design/Analysis&Synthesis/Netlist Viewers/RTL Viewer. Jeśli znajdziemy i otworzymy w nim realizację modułu c_mul, zobaczymy wynik podobny do tego z rysunku 6. Jest on bardzo podobny do naszego początkowego projektu z rysunku 2.
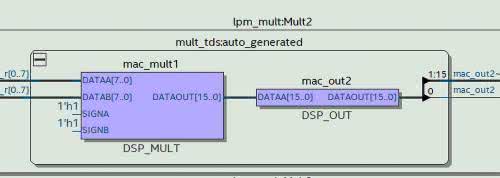
Jeżeli przejdziemy do widoku Technology Map Viewer (Post-Mapping), zaobserwujemy (rysunek 7), że tym razem znak mnożenia został zastąpiony nowym modułem. Kiedy go otworzymy, naciskając symbol (+), zobaczymy widok podobny do tego z rysunku 8. Widzimy na nim bloki DSP_MULT oraz DSP_OUT. Odpowiadają one sprzętowemu blokowi, który znajduje się wewnątrz układu FPGA. Poza wejściami danych DATAA i DATAB mamy także konfigurację znaku. W naszym przypadku oba z nich są na stałe ustawione na 1. Środowisko przyporządkowało tę stałą na podstawie parametru signed, w definicji wejściowych sygnałów.
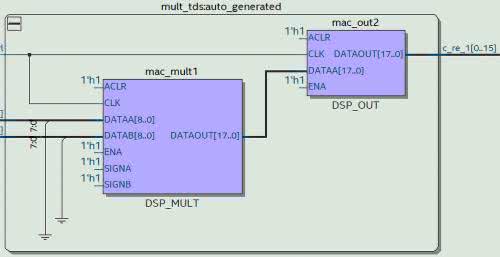
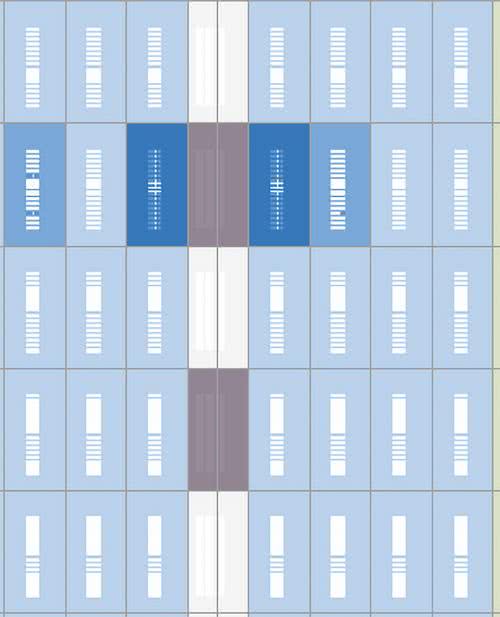
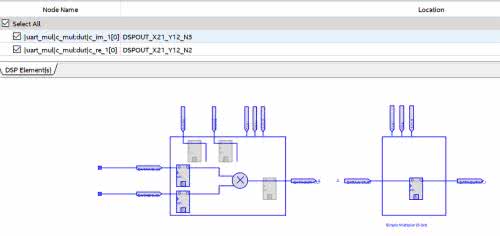
Jeżeli przejdziemy do widoku Technology Map Viewer (Post-Fitting), zobaczymy schemat podobny do rysunku 9. Widzimy, że główną różnicą są dodatkowe sygnały kontrolne enable oraz reset. Jak można zobaczyć w narzędziu Chip Planner, moduły mnożenia rozmieszczone są w układzie FPGA w jednej kolumnie. Jest ona oznaczona kolorem jasnoszarym. Wykorzystane moduły zostały zaznaczone kolorem ciemniejszym. Jak widzimy, nasz projekt zużył 2 bloki. Dokładniejszy opis bloku znajdziemy w programie Resource Property Editor. Fragment okna tego programu prezentuje rysunek 11. Na liście u góry rysunku, w pojedynczym module (oznaczonym jako X21_Y12), umieszczone zostały dwa 9-bitowe mnożenia.
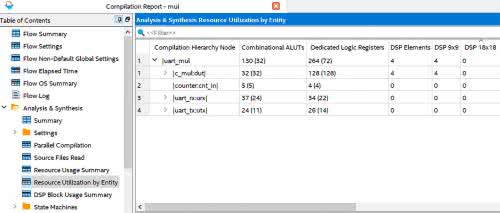
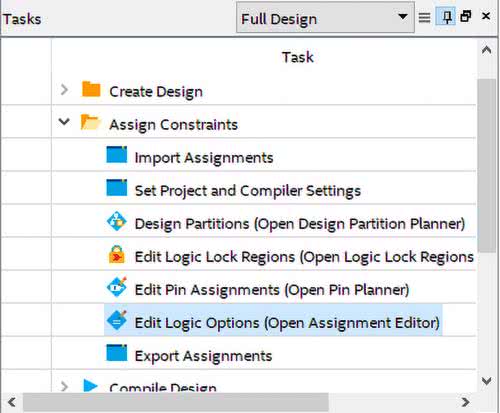
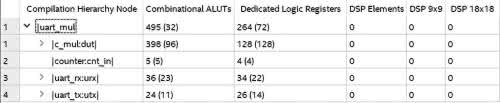
Warto jeszcze zobaczyć, jakie zasoby zużywa nasz moduł. W tym celu otwieramy raport kompilacji. Jak widzimy na rysunku 12, z zakładki Analysis & Synthesis wybieramy Resource Utilization by Entity. Na liście w centralnej części okna rozwijamy uart_mul. Zobaczymy, że blok c_mul zużył 32 bloki ALUT, 128 rejestrów i 4 elementy DSP (czyli mnożarki). Możemy zmienić konfigurację i wymusić, aby mnożenie zostało zrealizowane z elementów kombinacyjnych, a nie w odpowiednich blokach. W tym celu z panelu Tasks otwieramy Edit Logic Options. Pojawi się nowe okno podobne do tego z rysunku 14. Widzimy, że w tym miejscu także pojawia się konfiguracja wejść/wyjść, którą stworzyliśmy w narzędziu Pin Planner. Aby dodać nową pozycję, klikamy <<new>> w kolumnie Assignment Name. Z listy wybieramy opcję DSP_BLOCK_BALANCING. W kolumnie Value, z dostępnych na liście możliwości, wybieramy Logic Elements. Cała konfiguracja jest pokazana na rysunku 15. Możemy zapisać i uruchomić budowę powtórnie. Rysunek 16 pokazuje zużycie zasobów. Widzimy, że obecnie liczba elementów DSP jest równa 0. Liczba zużytych rejestrów nie uległa zmianie. Natomiast liczba elementów logicznych wzrosła ponaddziesięciokrotnie z 32 do 398.
Przywrócimy wykorzystanie sprzętowych mnożarek poprzez zmianę wartości w kolumnie Enabled (rysunek 14) na – No. Teraz zbudujmy projekt jeszcze raz i zaprogramujmy płytkę Rysino.
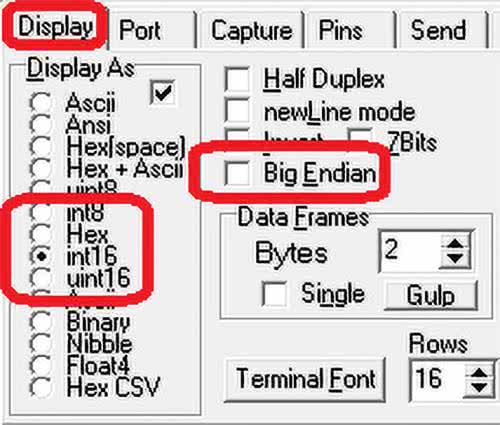
Do komunikacji użyjemy programu RealTerm. Po wyborze numeru prędkości i ustawieniu prędkości na 115200, przejdźmy do zakładki Display. Tutaj wybieramy tryb wyświetlania (Display As) na int16 – liczba 2-bajtowa ze znakiem. Na końcu jeszcze wyłączamy tryb Big Endian, odklikując znacznik.
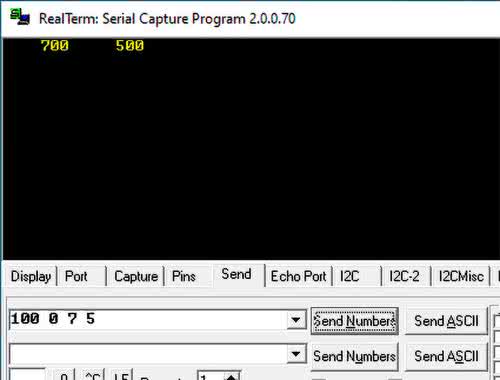
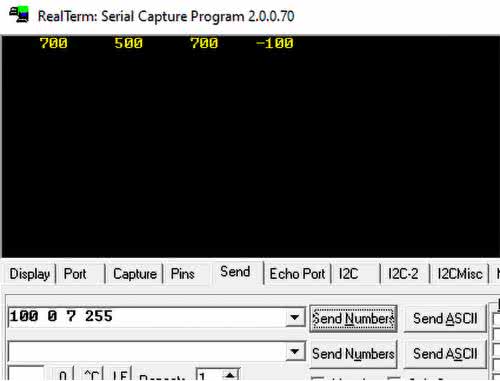
Aby wysłać dwie liczby zespolone, przechodzimy do zakładki Send (rysunek 18). W polu wpisujemy cztery liczby. Po kolei są to część rzeczywista i urojona obu czynników. W moim przypadku mnożę liczby 100+0j i 7+5j. Po kliknięciu Send Numbers, w konsoli pojawił się wynik: 700+500j. Niestety, nie jest obsługiwane przesyłanie liczb ujemnych, dlatego trzeba samemu „zmienić” liczbę ujemną, zapisaną w kodzie dopełnienia do dwóch, na odpowiadającą jej liczbę dodatnią. Przykładowo, na rysunku 19 przesłano liczby 100+0j i 7–1j. Przy wyświetlaniu zgodnie z konfiguracją, liczby ujemne są już obsługiwane.
Podsumowanie
Poznaliśmy nowy element układu FPGA – mnożarkę, nazywaną także blokiem DSP. Użyliśmy jej do implementacji mnożenia zespolonego. W kolejnym odcinku blok stanie się fragmentem naszej implementacji dyskretnej transformaty Fouriera.
Rafał Kozik
rafkozik@gmail.com
Bibliografia
[1] Repozytorium z przykładami – http://bit.ly/33uYPxs
[2] MAX 10 Embedded Multiplier Block Overview, https://intel.ly/2ZZDuxe
[3] Complex Multiplication, https://bit.ly/2EpkKzo

 Zaloguj
Zaloguj