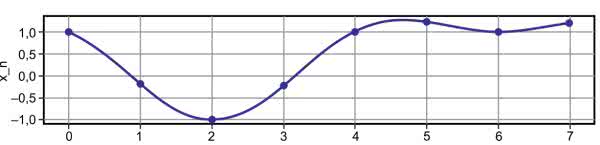
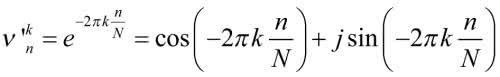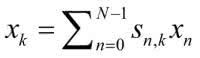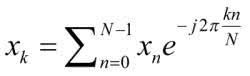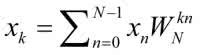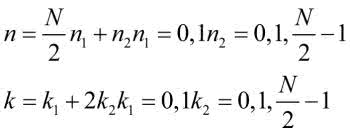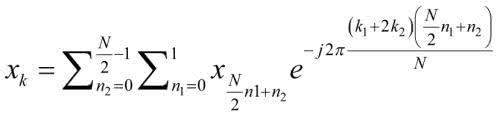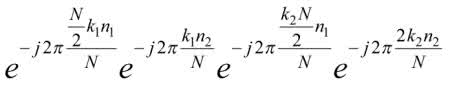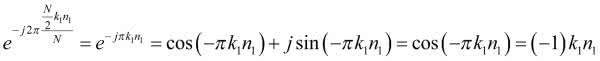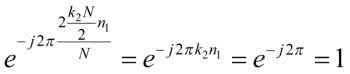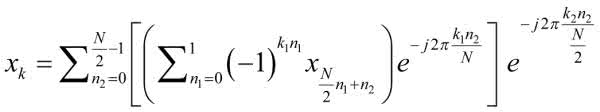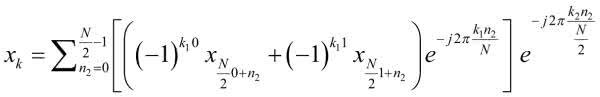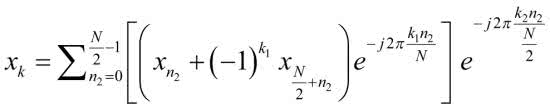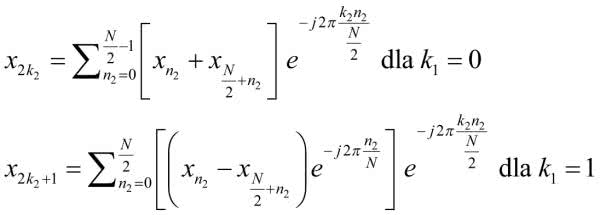Przed przystąpieniem do wykonywania eksperymentów, zachęcam do aktualizacji repozytorium z przykładami (poprzez wywołanie polecenia git pull) [1]. Rysunek 1 pokazuje przykładowy sygnał analogowy.
Został on spróbkowany w ośmiu, równo od siebie oddalonych punktach – są one zaznaczone na wykresie kropkami. Natomiast to, co zostaje z sygnału za przetwornikiem ADC, ilustruje rysunek 2.
Na pierwszy rzut oka ciężko dopatrzeć się w pojedynczych punktach pierwotnego sygnału, ale jeżeli spełnione jest twierdzenie o próbkowaniu, to zawarta jest w nich pełna informacja o przebiegu ciągłym. Twierdzenie mówi o tym, że częstotliwość próbkowania musi być dwa razy większa niż szerokość pasma badanego sygnału.
Wrócimy jednak do naszych próbek, które możemy przedstawić jako wektor o długości N=8:
W tym zapisie współczynniki odnoszą się do najprostszej bazy, składającej się z wektorów:
Krócej możemy zapisać ją za pomocą delty Kronecker:
Gdzie vk to kolejny wektor bazy, natomiast n jest indeksem elementu wewnątrz niego. Nie jest to jednak jedyna możliwa baza. Możemy na przykład zaproponować taką, która składa się z ciągów odpowiadających kolejnym (zespolonym) sygnałom sinusoidalnym:
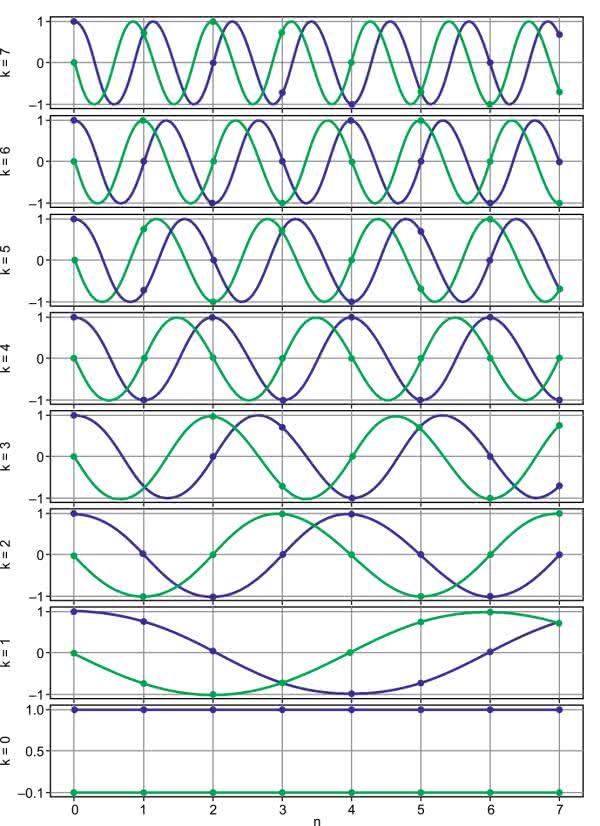
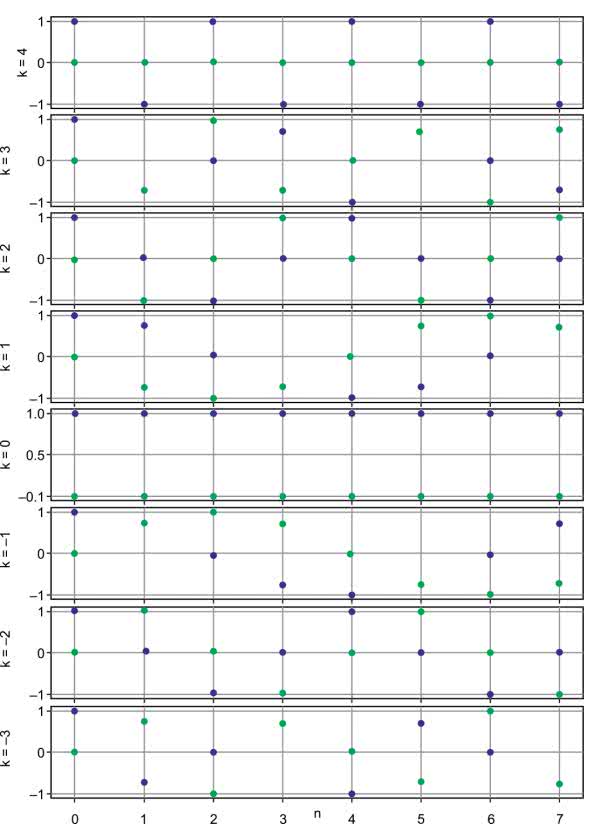
Kolejne wektory bazy pokazuje rysunek 3. Na wszystkich wykresach kolorem niebieskim oznaczono część rzeczywistą, a zielonym – urojoną.
Jeżeli więc zapiszemy nasz wektor w nowej bazie, kolejne współczynniki (teraz już zespolone) będą oznaczały amplitudę i fazę kolejnych składowych, występujących w sygnale. Zwracam uwagę, że częstotliwość k jest przy próbkowaniu równoważna częstotliwości k–N:
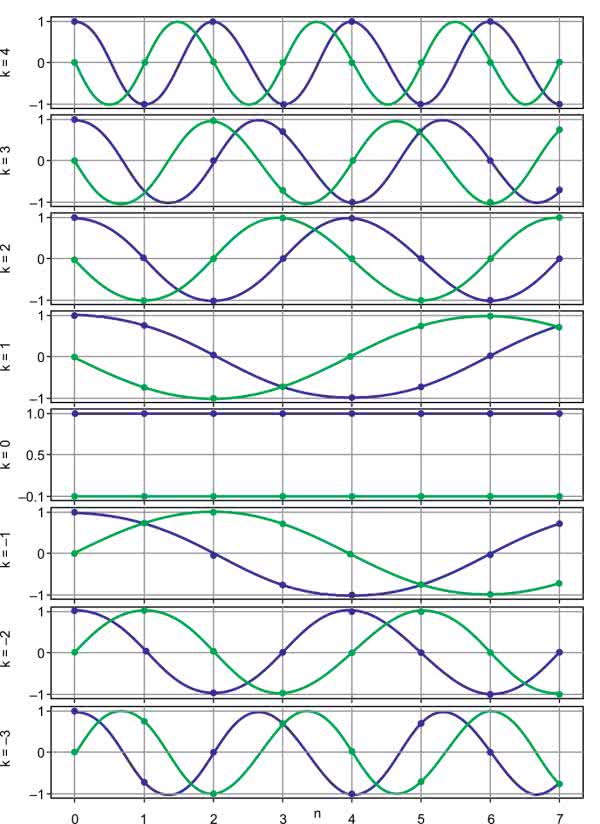
Ostatnia równość jest prawdziwa, ponieważ n jest zawsze liczbą całkowitą, a dodanie 2π do argumentu funkcji trygonometrycznej, nie powoduje zmiany wyniku. Dlatego częstotliwości 5, 6 i 7 możemy interpretować także jako –3, –2 i –1 – takie podejście pokazuje rysunek 4.
Warto zwrócić uwagę, że częstotliwości ujemne różnią się od dodatnich jedynie znakiem części urojonej. Jest to możliwe, ponieważ tak naprawdę interesują nas jedynie wartości w punktach, a nie całe krzywe. Zostały one narysowane na wykresie, ponieważ bez oznaczeń ciężko dojść, skąd się wzięły oraz co reprezentują poszczególne punkty – o czym można przekonać się, spoglądając na rysunek 5.
Aby przejść z jednej bazy do drugiej, potrzebujemy jeszcze macierzy przejścia. Składa się ona z kolejnych wektorów nowej bazy, wyrażonych we współczynnikach starej. W naszym przypadku jest ona dana wzorem:
Oznacza to, że jej kolejne elementy to:
Aby uzyskać wartości współczynników naszego wektora x, w nowej bazie musimy pomnożyć go przez macierz:
Rozpisując, otrzymujemy:
Po podstawieniu elementów macierzy z (5) otrzymujemy dobrze znany wzór na dyskretną transformatę Fouriera:
Gdzie zarówno n, jak i k, zmieniają się od 0 do N–1. Dla uproszczenia zapisów czasami stosuje się też oznaczenie:
Prowadzi to do krótszego zapisu:
Warto zauważyć, że dla sygnału rzeczywistego części urojone muszą się zredukować. Oznacza to, że współczynniki przy częstotliwościach dodatnich będą sprzężeniem odpowiadających im współczynników przy częstotliwościach ujemnych. Nie dotyczy to częstotliwości 0 oraz ![]()
Pozostaje jeszcze wykonanie obliczeń dla danych z rysunku 1. Otrzymana transformata to:
Kształt poszczególnych składowych pokazuje rysunek 6.
FFT, czyli sprytne obliczenia
Korzystając bezpośrednio z definicji, dojdziemy do tego, że aby obliczyć pojedynczy współczynnik, musimy wykonać N mnożeń zespolonych.
Ponieważ samych współczynników też jest N, łatwo obliczyć, że przy naiwnym podejściu niezbędnych jest N2 mnożeń zespolonych. Proponuję zamiast tego prosty trik, który przyspieszy obliczenia:
Stosując inne podstawienie, można uzyskać inne wersje szybkiej transformaty Fouriera [2]. My jednak prześledzimy tylko podstawowy przypadek, w którym uzyskamy obliczenie transformaty o rozmiarze N za pomocą dwóch transformat o połowę krótszych. Podstawiając do (10), otrzymamy:
Na początku zajmijmy się samą potęgą. Po wymnożeniu nawiasów otrzymamy:
Sumę w wykładniku możemy rozpisać jako mnożenie:
Spróbujmy uprościć poszczególne składniki:
Dzieje się tak, ponieważ iloczyn k1n1 może przyjąć jedynie wartość 0 albo 1. Jeszcze bardziej możemy uprościć trzeci iloczyn:
Ponieważ zarówno k2, jak i n1 są liczbami całkowitymi, mamy zawsze do czynienia z obrotem o pełny kąt 2π. Dlatego cały czynnik upraszcza się i jest zawsze równy 1. Korzystając z tych zależności, możemy teraz rozpisać (4) jako:
Rozpiszmy jeszcze wewnętrzną sumę. Ma ona w końcu jedynie dwa składniki:
Po usunięciu mnożeń razy 1 otrzymamy:
Gdy zasłonimy sobie nawias kwadratowy i przyjrzymy się pozostałej części wzoru, zauważymy coś ciekawego. Otóż cała reszta przypomina także transformatę Fouriera, ale tym razem o długości o połowę mniejszej. Rozpiszmy teraz jeszcze indeks k, osobno dla parzystych i nieparzystych współczynników, a otrzymamy:
Rozpisaliśmy transformatę Fouriera o długości N na dwie transformaty o mniejszej długości. Teraz musimy wykonać pewne działania na współczynnikach, a następnie policzyć jedną transformatę dla współczynników parzystych, a drugą dla nieparzystych. Jednak sądzę, że to dobry moment, aby zakończyć ten odcinek i dać czytelnikom czas na spokojne przeanalizowanie opisanych obliczeń.
Rafał Kozik
rafkozik@gmail.com
Przypisy:
[1] Repozytorium z przykładami: http://bit.ly/33uYPxs
[2] Lyons r.G., Wprowadzenie do cyfrowego przetwarzania sygnałów, Wydawnictwo Komunikacji i Łączności, Warszawa 2010
[3] Film prezentujący działanie FFT: https://bit.ly/35H0yTp

 Zaloguj
Zaloguj