Dlaczego nie przerzutnik T?
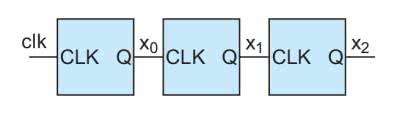
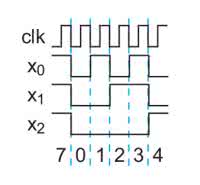
Najprostszą realizacją licznika binarnego jest kaskadowe połączenie przerzutników T. Konstrukcję taką pokazuje rysunek 1. Dla przypomnienia przerzutnik T jest to blok z jednym wejściem zegarowym (nazwijmy je CLK) oraz z jednym wyjściem (Q). Zbocze zegara powoduje zmianę stanu na jego wyjściu na przeciwny. Aby licznik zliczał w górę przerzutniki muszą reagować na ujemne zbocze zegara. Przebiegi czasowe w takim układzie pokazuje rysunek 2.
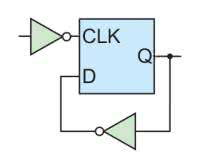
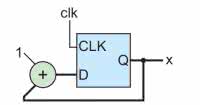
Nasz układ FPGA wyposażony jest w przerzutniki typu D reagujące na dodatnie zbocze. Jednak dałoby się z nich skonstruować przerzutniki reagujące na zbocze ujemne dodając dodatkową logikę jak pokazuje to rysunek 3. Takie rozwiązanie jednak nie jest zalecane. Powstały w ten sposób licznik jest asynchroniczny (ripple counter). Problemem jest tu szybkość propagacji sygnałów poprzez połączenia i tablice LUT oraz czasy reakcji przerzutników [1]. Zaleca się, aby logika zaimplementowana w układzie FPGA była synchronizowana wspólnym zegarem – czyli znajdowała się w jednej domenie zegarowej. W uproszczeniu można to rozumieć jako połączenie razem wszystkich wejść zegarowych przerzutników D.
Czasami zdarza się, że cześć bloków musi pracować na zegarze o innej częstotliwości. Pomiędzy takimi blokami konieczne są wtedy dodatkowe moduły synchronizujące sygnały. Noszą one nazwę CDC (clock domain crossing – przechodzenie pomiędzy domenami zegarowymi).
Do rozprowadzania sygnału zegarowego przygotowane są także osobne ścieżki połączeniowe nazywane w układzie MAX10 Global Clock Network (globalna sieć zegara) [2]. Więcej informacji odnośnie synchronizacji i taktowania w układach FPGA można znaleźć w wykładach [4] i [5].
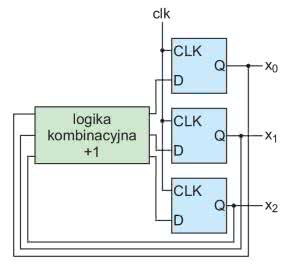
Wróćmy do naszego licznika, rysunek 4 przedstawia jego synchroniczną wersję. Tak jak poprzednio składa się on z trzech przerzutników D. Tym razem jednak są one taktowane wspólnym sygnałem zegarowym. Ich wyjścia wchodzą następnie na logikę kombinacyjną, która realizuje dodawanie jedynki. Tutaj już określenie maksymalnej częstotliwości zegara jest łatwiejsze. Jego okres musi być większy niż łączny czas ustawienia się nowego stanu na wyjściu przerzutnika, propagacji przez logikę i jego ponownego zapisu. W uproszeniu układ z rysunku 4 można przedstawić „wektorowo” jak pokazuje to rysunek 5. Pogrubiona linia obrazuje przepływ nie jednego, ale (w tym przypadku) trzech sygnałów.
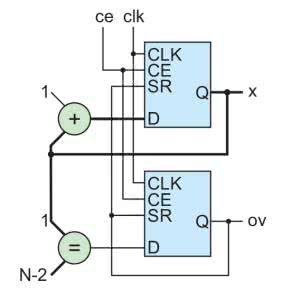
Poprzedni licznik zliczał od 0 do 7. Liczył więc modulo 8. Dla potęg dwójki następuje to automatycznie. Jednak aby zmienić ten zakres potrzebujemy dodatkowego kawałka logiki, który będzie odpowiadał za wyzerowanie licznika w odpowiednim momencie. Jego schemat jest pokazany na rysunku 6. Pozwala on na liczenie od 0 do N-1. Znajdujące się na nim przerzutniki D mają dwa dodatkowe wejścia.
Pierwszym z nich jest SR, czyli reset synchroniczny. Ustawienie na nim jedynki logicznej powoduje wyzerowanie liczniki podczas następnego zbocza narastającego, niezależnie od aktualnej wartości na wejściu D. Drugim z nich jest CE (clock enable – włącz zegar). Ustawienie na tym wejściu zera powoduje „wyłączenie” przerzutnika. Oba te wejścia zostały dodane, ponieważ przerzutniki D wbudowane w układ MAX10 są w nie wyposażone. Wyjaśnienia wymaga także nowy blok logiki kombinacyjnej oznaczony jako „=”. Na jego wyjściu jedynka pojawia się tylko gdy oba wektory wejściowe są takie same. Pozwoli nam on na generowanie dodatkowego sygnału wyjściowego OV (overflow) sygnalizującego przepełnienie się licznika.
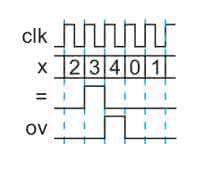
Początkowo mało intuicyjny jest fakt, że mimo iż liczymy do N-1, sygnał resetu generujemy już gdy wartość licznika jest równa N-2. Spowodowane jest to tym, że chcemy aby sygnał resetu nie był podawany bezpośrednio z logiki kombinacyjnej, ale został najpierw zapisany w rejestrze. Z tego powodu musimy ją wykrywać jeden takt zegara wcześniej. Dzięki temu, że licznik liczy po kolei możemy to zrealizować po prostu poprzez zmniejszenie liczby przy której zgłaszamy sygnał. Aby lepiej wyobrazić sobie jego działanie na rysunku 7 przedstawiony jest przypadek dla N=5.
Przebieg „=” oznaczający wyjście z bloku porównania ma stan wysoki podczas gdy x=3. Jednak zostaje on przepisany na wyjście ov dopiero na następnym takcie zegara, kiedy x osiągnie już wartość 4. Synchroniczny reset przerzutników D nastąpi dopiero na kolejnym zboczu zegara, co spowoduje, że kolejną wartością x będzie 0.
Licznik złożony z przerzutników T pozwala w łatwy sposób połączyć go kaskadowo z drugim licznikiem. Dla naszego licznika też jest to możliwe.
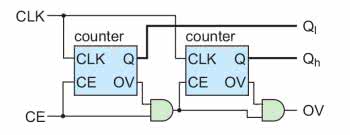
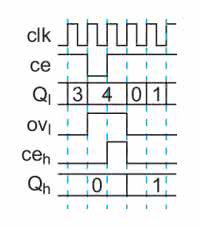
Użyjemy w tym celu dodanego ostatnio złącza CE. Schemat takiego połączenia pokazuje rysunek 8. Na wejście CE licznika podłączamy iloczyn logiczny (i) wyjścia OV poprzedniego licznika oraz wszystkich poprzednich złącz CE. Przebiegi czasowe w tak powstałym układzie przedstawia pokazuje rysunek 9.
Pierwszy licznik (Ql) liczy modulo 5. W momencie doliczenia do 4 na jego wyjściu OV pojawia się stan wysoki. Tutaj widzimy dlaczego wejście CEh drugiego licznika musi być iloczynem logicznym wyjścia OVl i CEl. Gdyby tego nie uwzględnić górny licznik został by zinkrementowany dwukrotnie.
Implementujemy licznik
Mamy już projekt modułu. Czas więc na jego implementację w języku SystemVerilog. Znajdziemy ją w repozytorium [6] w pliku 02_counter/counter.sv oraz na listingu 1. Jeżeli czytelnik sklonował już repozytorium podczas przeprowadzania eksperymentów z poprzedniej części, teraz wystarczy za pomocą polecenia pull pobrać najnowsze zmiany.
10 module counter #(
11 parameter N = 25,
12 parameter W = $clog2(N)
13 ) (
14 input wire clk,
15 input wire rst,
16 input wire ce,
17 output logic [W-1:0]q,
18 output logic ov
19 );
20 always_ff @(posedge clk or negedge rst)
21 if (!rst)
22 q <= ‘0;
23 else if (ce)
24 if (ov)
25 q <= ‘0;
26 else
27 q <= q + 1’b1;
28
29 always_ff @(posedge clk or negedge rst)
30 if (!rst)
31 ov <= ‘0;
32 else if (ce)
33 if (ov)
34 ov <= 1’b0;
35 else
36 ov <= (q == N-2);
37 endmodule
Dzięki dodaniu parametru N (w linii 11) nasz moduł może służyć jako licznik o dowolnej długości. Parametr W nie powinien być ustawiany, ale jest obliczany na podstawie poprzedniego. Funkcja $clog2 zwraca wartość logarytmu o podstawie 2 zaokrągloną w górę. Dzięki temu wiemy jakiej długości wektor jest potrzebny do przechowywania maksymalnej liczby.
Funkcje poszczególnych wejść i wyjść (linie 14...18) są takie same, jak omówione wcześniej. Wyjątkiem jest wejście rst, które służy jako asynchroniczny reset. Dzięki niemu w symulacji będziemy mogli zaczynać od ustalonego stanu, a podczas pracy ze sprzętem będziemy mogli zresetować układ za pomocą przycisku.
Logika jest zawarta w dwóch blokach always_ff: pierwszy z nich odpowiada za logikę licznika, a drugi wykrywa przepełnienie. Ponieważ zewnętrzny reset jest asynchroniczny musimy go dodać do listy. Ponieważ asynchroniczny reset przerzutników, które wchodzą w skład układy MAX10 jest wyzwalany stanem niskim, musimy wykrywać jego ujemne zbocze (negedge).
Wewnątrz bloku always_ff najpierw następuje sprawdzenie resetu, ponieważ ma on najwyższy priorytet. Potem, jeżeli na wejściu ce panuje stan wysoki następuje wyzerowanie stanu (gdy wystąpi przepełnienie), albo jego inkrementacja.
Kod bloku wykrywającego przepełnienie (linie 29...36) jest bardzo podobny. Sprawdzenie następuje za pomocą operator porównania ==. Działa on bardzo podobnie do swojego kuzyna znanego z języka C.
11 module counter_tb;
12 logic clk, rst, ce, ov1;
13
14 initial begin
15 clk <= ‘0;
16 forever #5 clk <= ~clk;
17 end
18
19 initial begin
20 rst <= 1’b0;
21 #10 rst <= 1’b1;
22 end
23
24 initial begin
25 ce <= 1’b1;
26 #20 ce <= 1’b0;
27 #20 ce <= 1’b1;
28 end
29
30 counter #(.N(10)) dut1 (
31 .clk(clk),
32 .rst(rst),
33 .ce(ce),
34 .q(),
35 .ov(ov1)
36 );
37
38 counter #(.N(3)) dut2 (
39 .clk(clk),
40 .rst(rst),
41 .ce(ce & ov1),
42 .q(),
43 .ov()
44 );
45 endmodule
Aby sprawdzić działanie użyjemy testbench przedstawiony na listingu 2. Znajdziemy go w pliku 02_counter/counter_tb.sv. Składa się on z dwóch liczników połączonych kaskadowo. Pierwszy z nich (dut1) liczy od 0 do 9, a drugi (dut2) od 0 do 2. Łącznie można więc go traktować jako dziesiątkowy licznik liczący od 0 do 29. Wymuszenia są generowane w trzech niezależnych blokach initial. Pierwszy z nich dostarcza zegar o częstotliwości 10 jednostek czasu. Drugi odpowiada za globalny reset, który jest wymuszony przez pierwsze 10 jednostek symulacji. Ostatni wyłącza sygnał ce pomiędzy 20, a 40 jednostką.
08 vlib work
09
10 vlog counter.sv
11 vlog counter_tb.sv
12
13 vsim -novopt work.counter_tb
14
15 add wave -position end sim:/counter_tb/clk
16 add wave -position end sim:/counter_tb/rst
17 add wave -position end sim:/counter_tb/ce
18 add wave -position end -unsigned sim:/counter_tb/dut1/q
19 add wave -position end sim:/counter_tb/dut1/ov
20 add wave -position end sim:/counter_tb/dut2/ce
21 add wave -position end -unsigned sim:/counter_tb/dut2/q
22 add wave -position end sim:/counter_tb/dut2/ov
23
24 run 40us
25 wave zoom full
Aby ułatwić uruchomienie symulacji powstał skrypt counter_sim.do. Jest on pokazany na listingu 3. Najpierw wybiera domyślną bibliotekę (linia 8), a następnie realizuje on kompilację źródeł (linie 10-11) i uruchamia symulację (linia 13). Linie od 15 do 22 odpowiadają za wyświetlenie przebiegów czasowych dla interesujących nas sygnałów. Warto zwrócić uwagę na linie 18 i 21, gdzie za pomocą flagi -unsigned określiliśmy, że wektory mają być traktowane jako liczba bez znaku i wyświetlone w systemie dziesiętnym. Polecenie run (linia 24) powoduje wykonanie 40 ms symulacji. Ostatnie polecenie dostosowuje powiększenie w taki sposób, abyśmy na ekranie wydzieli całą symulację. Teraz możemy uruchomić program ModelSim i za pomocą polecenia:
cd C:/sv/counter
Przejdziemy do folderu zawierającego nasz projekt (oczywiście należy zmienić ścieżkę na tą, pod którą sklonowaliśmy repozytorium z projektem pamiętając o zamianie backslashy \ na slashe /). Uruchamiamy skrypt rozkazem:
do counter_sim.do
Po jego wykonaniu zobaczymy wynik podobny do pokazanego na rysunku 10. Przedstawia on pełny obieg od 0 do 29.
Czas na sprzęt
Sprawdziliśmy już w symulacji, że przygotowany przez nas moduł licznika działa. Możemy więc teraz przygotować się do jego uruchomienia w sprzęcie. Dysponujemy generatorem kwarcowym o częstotliwości 8 MHz i ośmioma diodami LED. Będziemy na nich wyświetlać binarną wartość licznika zwiększanego co 100 ms. W tym celu powstał moduł przedstawiony na listingu 4 (i w pliku 02_counter/clk_counter.sv). Licznik counter1 służy do dzielenia zegara przez 800000. Dzięki czemu uzyskamy sygnał CE, który podłączymy do drugiego licznika counter2.
10 module clk_counter (
11 input wire clk,
12 input wire rst,
13 output logic [7:0]led
14 );
15 logic t100ms;
16
17 counter #(
18 .N(800000)
19 ) counter1 (
20 .clk(clk),
21 .rst(rst),
22 .ce(1’b1),
23 .q(),
24 .ov(t100ms)
25 );
26
27 counter #(
28 .N(256)
29 ) counter2 (
30 .clk(clk),
31 .rst(rst),
32 .ce(t100ms),
33 .q(led),
34 .ov()
35 );
36 endmodule
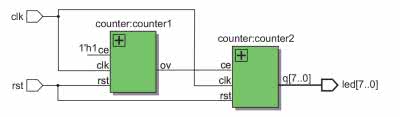
Tworzenie nowego projektu prześledziliśmy w poprzedniej części. Dlatego tym razem moduł został już dodany do projektu, który znajdziemy w pliku regs\counter\clk_counter.qpf. Możemy go otworzyć w środowisku Quartus. Także wyjścia modułów zostały już podłączone do pinów układu FPGA. Zsyntezujmy go uruchamiając polecenie Compile Design i przyglądnijmy się uzyskanym wynikom. Zacznijmy od znanego już nam narzędzia RTL Viewer. Dzięki temu, że podzieliliśmy projekt na moduły najpierw zobaczymy tylko połączenia pomiędzy nimi, co zostało pokazane na rysunku 11.
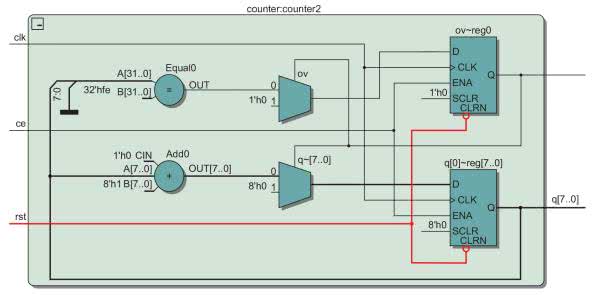
Dopiero po kliknięciu na znak plus (+) znajdujący się w prawym górnym rogu elementu pojawi się jego wewnętrzna struktura. Jak widzimy na rysunku 12 jest ona bardzo podobna do naszego projektu z rysunku 6. Jednak zamiast wykorzystać synchroniczny reset zerowanie zostało zamodelowane za pomocą zewnętrznych multiplekserów.
Przejdźmy jednak do bardziej szczegółowego widoku jaki zobaczymy po wybraniu Technology Map Viewer (Post-Mapping). Tutaj nie jest już pokazany ogólny schemat RTL, ale oparty o elementy dostępne w strukturze układu FPGA. Zobaczymy wynik podobny do tego z rysunku 13, ale bardziej poplątany. Możemy go troszeczkę uporządkować. Chwycenie bloku myszką przy jednoczesnym trzymaniu klawisza shift pozwala na jego przesunięcie.
Widzimy, że tym razem wykorzystany jest sygnał synchronicznego resetu opisany jako SCLR (synchronius clear). Warto także zwrócić uwagę, że przy implementacji dodawania użyto ścieżki przeniesienia łączącej wyjścia COUT z wyjściami CIN sąsiednich bloków LUT. Realizacja porównania zajmuje 3 osobne bloki LUT oznaczone jako ov~0, ov~1 i ov~2 oraz jeden rejestr ov.
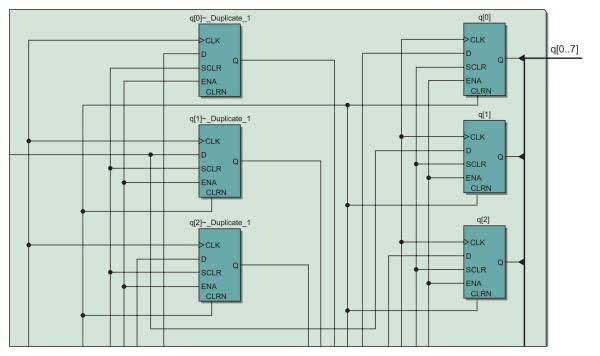
Kolejna ciekawostka czeka nas, gdy otworzymy widok Technology Map Viewer (Post-Fitting). Fragment uzyskanego wyniku pokazuje rysunek 14.
Okazuje się, że przerzutniki, do których zapisane jest wyjście zostały zdublowane. Gdy przyjrzymy się rysunkowi dokładniej zauważymy, że rejestry oznaczone jako duplicate są użyte jako wejścia dla logiki kombinacyjnej realizującej zliczanie. Natomiast wyjścia pozostałych są wyprowadzone na zewnątrz.
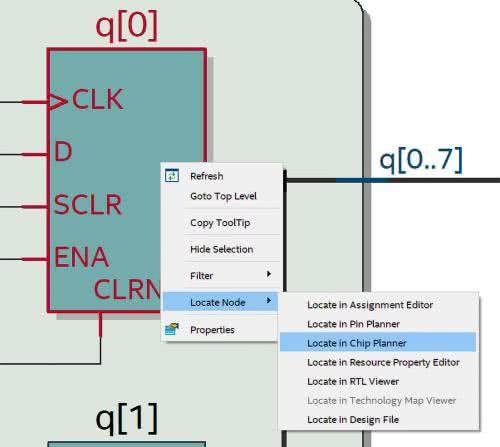
Sytuacja wyjaśni się, gdy klikniemy go prawym przyciskiem myszy i z menu wybierzemy opcję Locate Node – Locate in Chip Planner (rysunek 15).
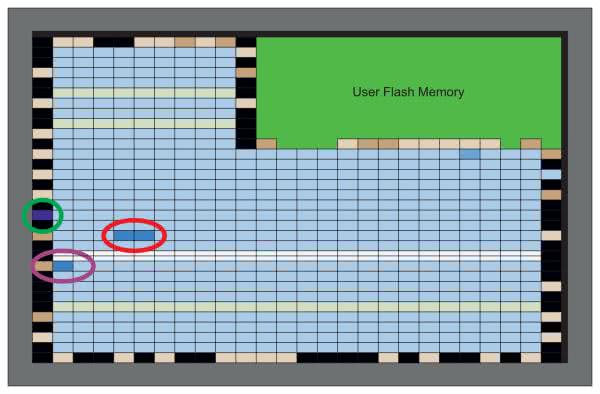
Na rysunku 16 widzimy rozlokowanie poszczególnych elementów logiki w układzie FPGA. Zduplikowany rejestr został zaznaczony zielonym okręgiem. Został on zlokalizowany na samej krawędzi układu. Gdy powiększymy to miejsce zobaczymy, że został użyty rejestr znajdujący się w strukturze odpowiadaj za sterowanie wyjściami.
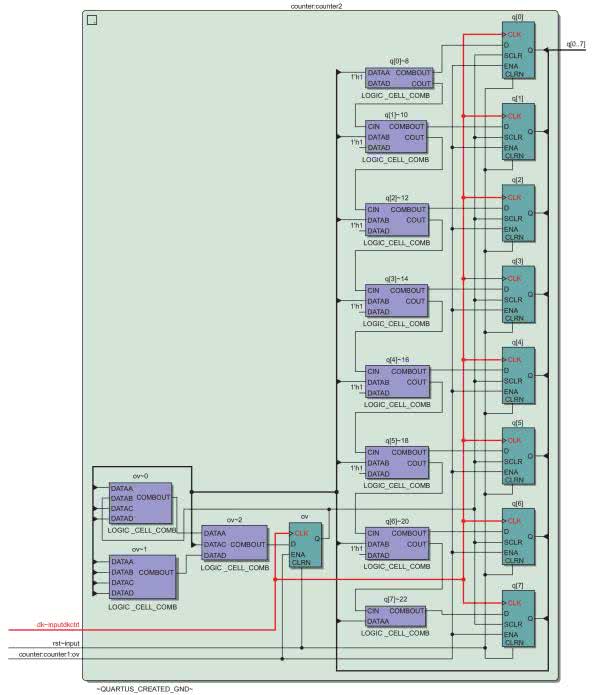
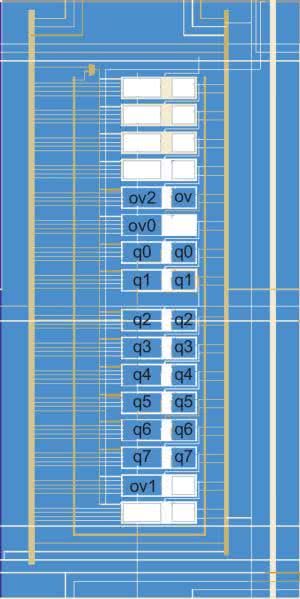
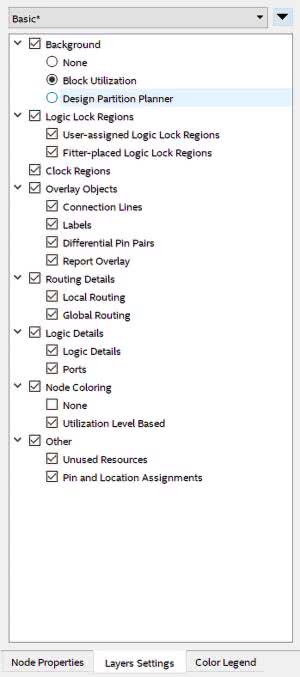
Miejsce oznaczone czerwonym okręgiem to lokalizacja licznika 1, a fioletowym to licznika 2. Na rysunku 17 widzimy powiększenie LAB w którym zaimplementowany został ten drugi. Dodatkowo na rysunku podpisano którym częściom projektu odpowiadają poszczególne struktury. Tutaj warto wspomnieć, że LAB jest skrótem od Logic Array Block i składa się z 16 sąsiadujących elementów logicznych LE, połączeń pomiędzy nimi oraz sygnałów kontrolnych. Jeżeli nawet po powiększeniu nie widzimy wszystkich elementów pokazanych na rysunku 17 możemy zmienić ich widoczność korzystając z panelu Layers Settings pokazanego na rysunku 18.
O zegarze
W początkowej części zostało wspominanie, że narzędzie sprawdza dla nas z jaką maksymalnie częstotliwością możemy uruchomić nasz wynikowy projekt. Możemy także dodać odpowiednie „więzy”, które zostaną wzięte pod uwagę podczas syntezy. Służy do tego specjalny format plików – sdc. Jego nazwa jest skrótem od Synopsys Design Constraints. Więcej na temat tego formatu można znaleźć w [7]. W naszym projekcie znajduje się on w pliku 02_counter/clk_counter.sdc. Aby został uwzględniony podczas syntezy po prostu dodajemy go do projektu. Jego zawartość pokazuje listing 5.
05 create_clock -name {clk} -period 125.000 -waveform { 0.000 62.500 } [get_ports { clk }]
06
07 set_input_delay -clock { clk } 2 [get_ports {rst}
08 set_output_delay -clock { clk } 2 [get_ports {led[0] led[1] led[2] led[3] led[4] led[5] led[6] led[7]}]
Jak widzimy jest bardzo krótki. W linii 5 został opisany sygnał zegarowy. Po fladze -name podana jest jego nazwa: clk. Okres (period) został ustawiony na 125 ns, a wypełnienie na 50%. Odpowiada to parametrom generatora kwarcowego umieszczonego na płytce. Na samym końcu przypisano, że w projekcie odpowiada mu port o nazwie clk. W dwóch kolejnych liniach znajdują się dodatkowe więzy opisujące jakie opóźnienia mogą wystąpić na wejściach (linia 7) i wyjściach (linia 8) układu. W tym przypadku przyjęto, że wynoszą one 2 ns względem sygnału zegarowego.
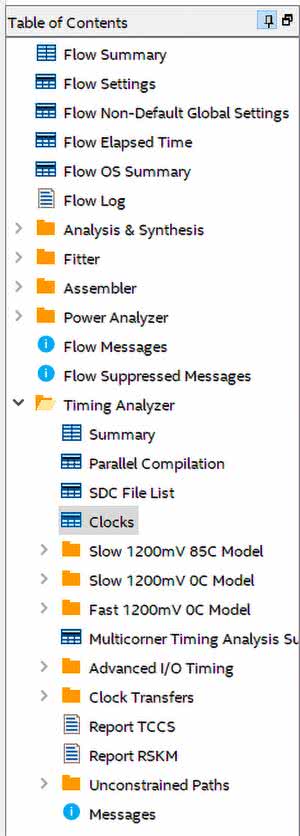
Aby zapoznać się z wynikami odnośnie czasów z panelu po lewej stronie programu Quartus wybieramy opcję Timing Analyzer – Clocks (rysunek 19).
W centralnej części pojawią się wtedy informację o wykrytych zegarach, co zostało pokazane na rysunku 20.
Aby zobaczyć z jaką maksymalna częstotliwością możemy taktować nasz projekt wybieramy opcję Slow 1200 mV 85C i zaznaczamy opcję Fmax Summary. Jak widzimy na rysunku 21 w przypadku naszego projektu jest to nieco ponad 73 MHz. Mamy więc bardzo duży zapas względem podłączonego sygnału zegarowego. Gdy wybierzemy drugą opcję Slow 1200 mV 0C zobaczymy, że częstotliwość ta mocno zależy od temperatury.
Gdy schłodzimy układ z 85°C do 0°C maksymalna częstotliwość pracy wzrasta do ponad 82 MHz. W naszym prostym projekcie częstotliwość zegara, czy odpowiednio zdefiniowanie opóźnienia na wejściach, czy wyjściach nie mają dużego znaczenia. Jednak przy bardziej złożonych projektach, czy dla bardziej wymagających peryferiów (takich jak na przykład pamięć RAM) ich poprawne określenie jest kluczowe dla poprawnej pracy projektu.
Podsumowanie
Na koniec zostało nam uruchomienie projektu w sprzęcie. W tym celu wybieramy opcję Program Device i po połączeniu z płytką klikamy start. Teraz możemy już cieszyć oko migoczącymi diodami, myśląc przy tym o całej technologi, która stoi za tym widokiem.
W następnym odcinku przejdziemy do spraw bardziej praktycznych. Stworzymy moduł pozwalający na usunięcie drgań styków oraz podłączymy do płytki enkoder impulsowy.
Rafał Kozik
rafkozik@gmail.com
Literatura:
[1] Quartus II Handbook Version 9.1 Volume 1: Design and Synthesis, Chapter 5. Design Recommendations for Altera Devices and the Quartus II Design Assistant, https://intel.ly/2RxAYsS
[2] Intel® MAX® 10 Clocking and PLL User Guide, https://intel.ly/2tFzcOi
[3] Advance Synthesis Cookbook, https://intel.ly/2RcIp9R
[4] Wawrzynek J., Circuit Timing, http://bit.ly/37bO3yM
[5] Wawrzynek J., Power/clock distribution, http://bit.ly/2RdJq1u
[6] Repozytorium z kodem przykładów http://bit.ly/33uYPxs
[7] SDC and TimeQuest API Reference Manual, https://intel.ly/38uy9zQ

 Zaloguj
Zaloguj