Symulacja i pomiar czyli LTspice i Analog Discovery 2 w rękach konstruktora (4). Pomiar pojemności mostkiem Wheatstone’a

Fotografia 1. Charles Wheatstone (źródło http://bit.ly/2MYibFV)

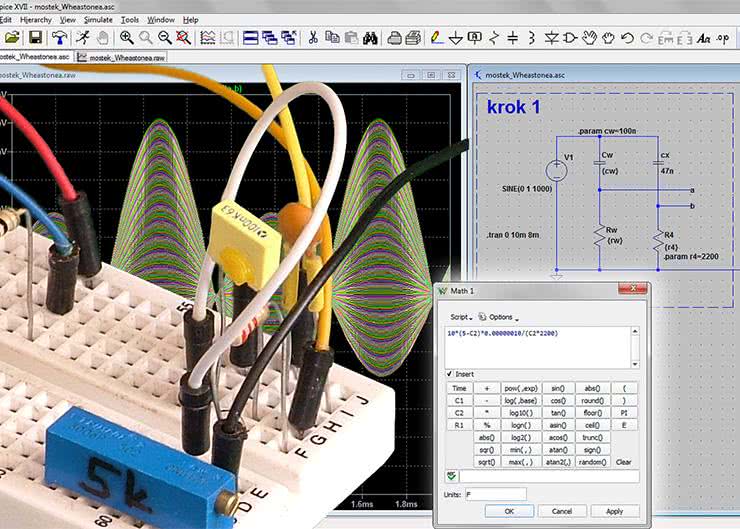
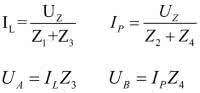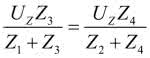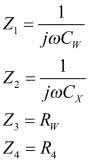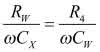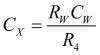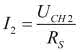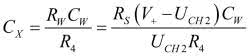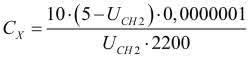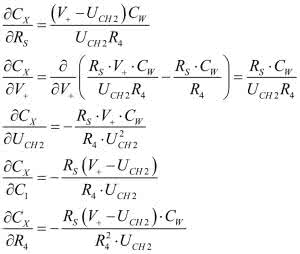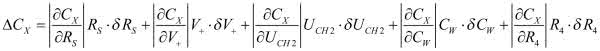Charles Wheatstone (fotografia 1) miał szczęście urodzić się w roku 1802, co dawało mu szansę znalezienia się w zaszczytnym gronie wielu dziewiętnastowiecznych odkrywców. Początkowo jednak nic takiego biegu wydarzeń nie wróżyło, gdyż ojciec małego Charlesa, jako zawodowy muzyk i producent instrumentów muzycznych pragnął podobnie wykształcić syna. Dbał zresztą o to należycie posyłając go do dobrych szkół. Plany ojca wkrótce się spełniły. Charles zainteresował się muzyką, terminował nawet w fabryce instrumentów. Nabył w niej praktycznych umiejętności i doświadczenia w zakresie budowy przyrządów precyzyjnych, co zaowocowało skonstruowaniem własnej harmonii. Szybko jednak okazało się, że muzyka nie była jedyną pasją Charlesa Wheatstone’a. Interesował się też m.in. optyką i elektrycznością. W 1837 roku opracował pierwszy telegraf elektryczny, ale jego najbardziej znanym wynalazkiem jest mostek prądu stałego pozwalający na bardzo precyzyjny pomiar rezystancji. My spróbujemy użyć tego urządzenia do pomiaru pojemności, ale przecież mostkiem prądu stałego raczej nie da się mierzyć pojemności. Pierwszą zatem modyfikacją będzie zasilenie mostka napięciem zmiennym i przyjęcie, że wszystkie elementy mostka są impedancjami, nie rezystancjami. Podobny tok rozumowania przeprowadził prawdopodobnie inny wynalazca Max Karl Werner Wien (1866-1938) opracowując swoją wersję mostka, ale czy jego modyfikacje były prowadzone w celu uzyskania narzędzia do pomiaru pojemności?

Przygotowanie do pomiarów - obliczenia

Rysunek 1. Schemat mostka Wheastone’a z impedancjami zamiast rezystancji

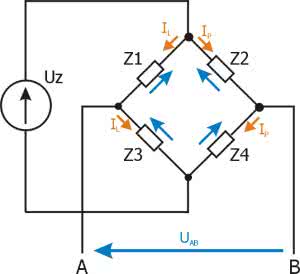
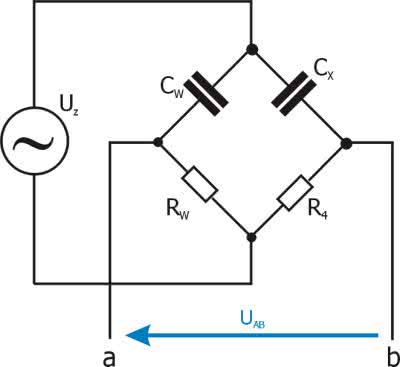
Wróćmy zatem do mostka Wheatstone’a. W trzech jego gałęziach były umieszczone rezystory o znanych wartościach, dodatkowo jeden z nich był regulowany. Badaną rezystancję umieszczano w czwartej gałęzi. Zasada pomiaru polegała na zrównoważeniu mostka za pomocą regulowanej oporności, a następnie obliczeniu rezystancji mierzonej na podstawie zależności wyznaczającej warunek równowagi mostka. W naszej konstrukcji rezystancje zastąpimy impedancjami (rysunek 1). Musimy wyznaczyć warunek równowagi mostka. Zakładamy, że obciążenie mostka jest pomijalne, czyli traktujemy go tak, jakby nie był obciążony w ogóle. Wynika z tego, że prąd I_L płynie zarówno przez impedancję Z₁, jak i przez Z₃. Podobnie prąd I_P płynie przez impedancje Z₂ i Z₄. Prądy te są równe:

Napięcie wyjściowe między węzłami A i B jest równe:

U_AB = U_A - U_B

W stanie równowagi jest ono równe 0, wynika z tego zależność:

stąd:

Z₃(Z₂ + Z₄) = Z₄(Z₁ + Z₃)

i ostatecznie:

Z₂Z₃ = Z₁Z₄               (1)

Rysunek 2. Schemat mostka, który zastosowano w pomiarach

Gdybyśmy zasilili mostek napięciem stałym a impedancje zamienili rezystancjami otrzymalibyśmy wariant Charlesa Wheatstone’a, jednak mostek ten chcemy przystosować do pomiaru pojemności. Dokonujemy więc modyfikacji polegającej na zastąpieniu rezystorów górnych gałęzi pojemnościami (rysunek 2), przy czym jedna z nich – C_X będzie pojemnością mierzoną, natomiast C_W będzie dokładnie znaną pojemnością wzorcową. Zmodyfikujmy teraz warunek równowagi mostka. Ogólne impedancje zastępujemy przyjętymi elementami, a więc:

Warunek równowagi ma teraz postać:

z czego wynika, że mierzona pojemność jest równa:

(2)

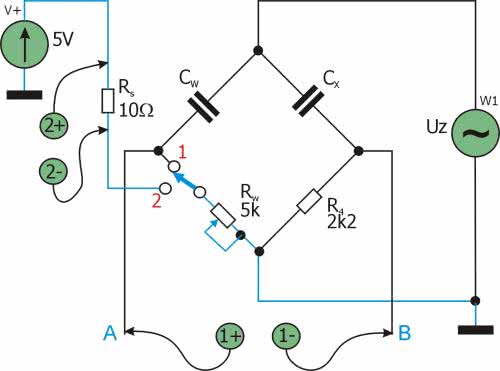
Mamy wszystko, co jest teoretycznie potrzebne do pomiaru pojemności C_X . Spróbujmy jeszcze nieco usprawnić nasz układ pomiarowy tak, aby wszystkie czynności mogły być wykonane wyłącznie za pomocą Analog Discovery 2. Jak wynika z zależności (2) pojemność C_X jest zależna od elementów stałych o znanych wartościach tj. C_W i R₄, a także od regulowanej rezystancji wzorcowej R_W. Rezystorem R_W będzie w naszym układzie precyzyjny potencjometr wieloobrotowy. Zmodyfikujmy układ tak, aby możliwe było mierzenie jego rezystancji. Trudność polega na tym, że przyrząd Analog Discovery 2 nie ma wbudowanego omomierza. Pomiar będzie więc 2-etapowy. W pierwszym kroku zrównoważymy mostek kręcąc suwakiem potencjometru R_W i obserwując jednocześnie na oscyloskopie napięcie wyjściowe. W drugim kroku rezystor R_W zostanie odłączony od mostka i dołączony do źródła napięcia stałego 5 V przez rezystor szeregowy R_S. Umożliwi on zmierzenie prądu płynącego w 2 kroku przez rezystor R_W a znając prąd i napięcie będzie już można obliczyć rezystancję R_W z prawa Ohma. Schemat pomiarowy całego stanowiska pokazano na rysunku 3. Źródło dodatniego napięcia stałego V+ jest dostępne w Analog Discovery 2, W₁ to 1 kanał generatora arbitralnego wytwarzający sygnał sinusoidalny o częstotliwości 1000 Hz i amplitudzie 3 V. Pierwszy kanał oscyloskopu dołączamy bezpośrednio do punktów „a” i „b” korzystając z możliwości różnicowego trybu pracy wejścia. Drugi kanał będzie mierzył różnicowe napięcie na rezystorze szeregowym R_S o znanej oporności 10 V. Analog Discovery 2 ma możliwość definiowania własnych wyrażeń matematycznych służących do obliczania wartości mierzonego parametru. Skorzystamy z tej cechy tak, aby w drugim kroku przyrząd podawał obliczony wynik uwalniając nas od obliczeń. W tym celu oporność R_W we wzorze (2) należy przedstawić tak, aby odpowiadała wielkościom występującym lub mierzonym w rzeczywistości. Są to: V+ = 5 V, R_S=10 Ω, UCH2 – napięcie zmierzone 2 kanałem oscyloskopu zależne od ustawionej rezystancji potencjometru RW. Zakładamy ponadto, że rezystor R4 będzie miał oporność 2200 V, a pojemność kondensatora wzorcowego C_W będzie równa 100 nF.

Rysunek 3. Schemat pomiarowy z użyciem zestawu Analog Discovery 2

Rozpatrując obwód zastosowany w drugim kroku pomiaru zawierający źródło napięcia V+, rezystor RS, przełącznik ustawiony w pozycji 2 i rezystor RW można dla niego zapisać równanie:

V₊ – I₂R_S – I₂R_W = 0

przy czym

gdzie U_CH2 – napięcie zmierzone 2 kanałem oscyloskopu.

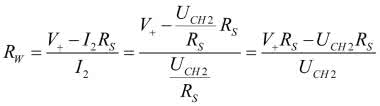
Z zależności tej wynika, że rezystancja potencjometru R_W jest równa: 

Powyższą zależność można już podstawić do wyrażenia (2), co pozwoli bezpośrednio obliczyć pojemność mierzoną na podstawie danych uzyskanych z narzędzi pomiarowych Analog Discovery 2.

                                                                                                                                 (3)
W wyrażeniu zastosowanym w Analog Discovery 2 wpisujemy konkretne wartości liczbowe, które przyjęliśmy wcześniej. Mamy więc ostatecznie:

                                                                                                                                 (4)
Taką formułę trzeba będzie zapisać w odpowiednim polu programu Waveforms. Liczba 10 widniejąca w liczniku reprezentuje rezystancję rezystora szeregowego, natomiast liczba 0,0000001 to pojemność wzorcowa. Celowo nie wymnożono ich ze sobą, aby można było później ewentualnie wpisać w formule Analog Discovery 2 dokładne wartości tych elementów zmierzone wcześniej precyzyjnym miernikiem.

Wykonamy pomiary dwóch kondensatorów. Pierwszy z nich będzie miał pojemność 100 nF, drugi 47 nF. W obu przypadkach zastosujemy ten sam kondensator wzorcowy C_W o pojemności 100 nF. Teoretycznie, dla zapewnienia symetrii układu pojemność ta powinna być jak najbliższa pojemności mierzonej, ale nie jest to warunek, który musi być bezwzględnie spełniony. Nasuwa się też pytanie: czy na wynik pomiaru ma również wpływ częstotliwość zasilania mostka? Jak widać, we wzorze (2) częstotliwość nie występuje, więc teoretycznie nie. Trzeba jednak pamiętać, że reaktancje obu kondensatorów są zależne od częstotliwości. W zależności od pojemności kondensatorów mostka i częstotliwości napięcia zasilającego będzie się zmieniał stosunek podziału napięć między kondensatorami i rezystorami. Największą precyzję regulacji uzyskamy, gdy napięcie zasilając będzie dzielone mniej więcej w połowie między kondensatorem a rezystorem jednej gałęzi mostka. Można więc rozpatrzyć wprowadzenie dodatkowego kroku pomiarowego, w którym po wstępnym zrównoważeniu mostka zostanie dobrana częstotliwość napięcia zasilającego tak, aby w napięcie punktach „a” i „b” było równe mniej więcej połowie napięcia zasilającego.

Pomiar, krok 1 - równoważenie mostka

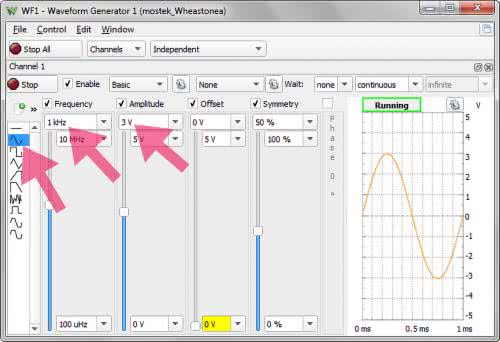
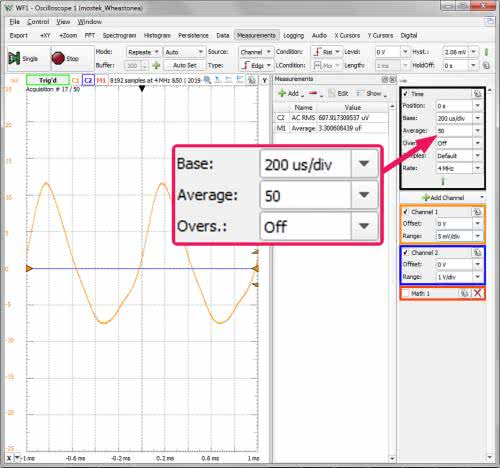
Mamy już wszystkie dane, przystępujemy więc do pomiarów. Układ tradycyjnie montujemy na płytce stykowej (fotografia 2). Nie stosujemy mechanicznego przełącznika widocznego na schemacie. Zamiast niego po prostu przepniemy kabelek bezpośrednio na płytce do odpowiedniego styku. W pierwszym kroku potrzebny będzie oscyloskop i generator arbitralny. Narzędzia te uruchamiamy z zestawu Analog Discovery 2. W generatorze wybieramy przebieg sinusoidalny, ustawiamy częstotliwość 1 kHz i amplitudę 3 V (rysunek 4). W oscyloskopie natomiast wybieramy podstawę czasu 200 ms/dz, czułość kanału 1. 500 mV/dz, wyzwalanie z kanału 1. Uruchamiamy oba przyrządy i kręcąc potencjometrem RW obserwujemy przebieg z kanału 1. Obracając suwak z jednego skrajnego położenia w drugie zaobserwujemy wyraźne minimum mierzonego napięcia. W miarę zbliżania się do tego minimum można stopniowo zwiększać czułość kanału 1. Niestety, całkowite zero jest trudne do uzyskania. W moim układzie uznałem, że mostek jest zrównoważony, gdy napięcie wyglądało tak, jak na rysunku 5. W celu uzyskania większej precyzji podczas równoważenia mostka można włączyć uśrednianie. Ja zastosowałem uśrednianie 50 akwizycji, a jako zero przyjąłem minimum napięcia AC RMS mierzonego w kanale 1 oscyloskopu.

Fotografia 2. Układ pomiarowy zmontowany na płytce stykowej

Rysunek 4. Parametry generatora ustawione w Analog Discovery 2

Można, a nawet należy zadać sobie pytanie, dlaczego nie jest możliwe uzyskanie idealnego zera? Prawdopodobnie jest to spowodowane różnicowym charakterem pomiaru. Najdrobniejsze przesunięcia fazowe wynikające choćby z pojemności układowych, mogą być przyczyną powstawania przebiegów o niezerowej amplitudzie. Nie przejmowałbym się jednak problemami tego typu, gdyż i tak nie spodziewam się dużej dokładności tego pomiaru.

Z zerowaniem mostka związany jest jeszcze zakres regulacji. Należało wybrać kompromis pomiędzy dokładnością i zakresem zerowania. Jak wynika z formuły (2) kondensator mierzony może być co najwyżej R_W/R₄ razy większy niż kondensator wzorcowy. W naszym przypadku jest to 2,27. Nie jest to dużo. Od dołu natomiast jest ograniczony możliwością wyznaczania małych rezystancji, co fizycznie oznacza pomiar małych prądów. Tu już zaczynają być istotne zagadnienia takie jak: rozdzielczość przetwornika A/C, szumy itp.

Rysunek 5. Przebieg występujący w stanie zrównoważenia mostka

Pomiar, krok 2 - pomiar rezystancji RW i obliczenie mierzonej pojemności

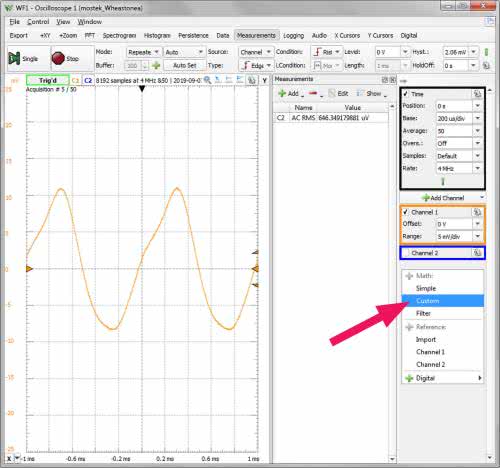
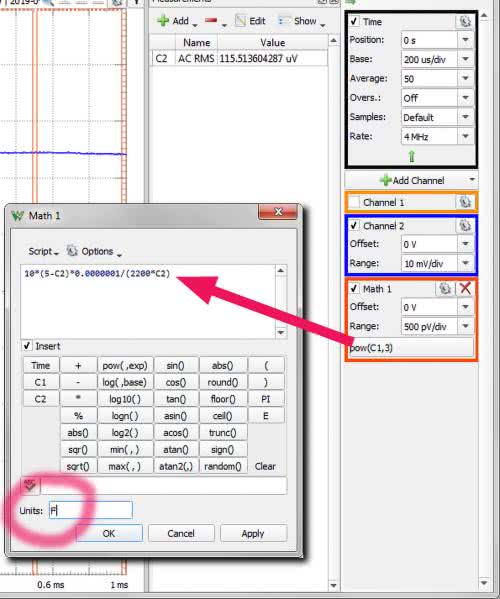
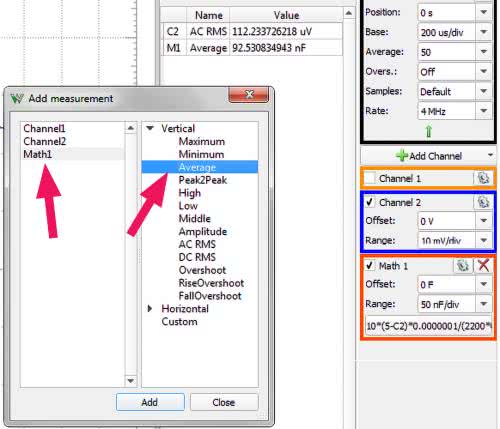
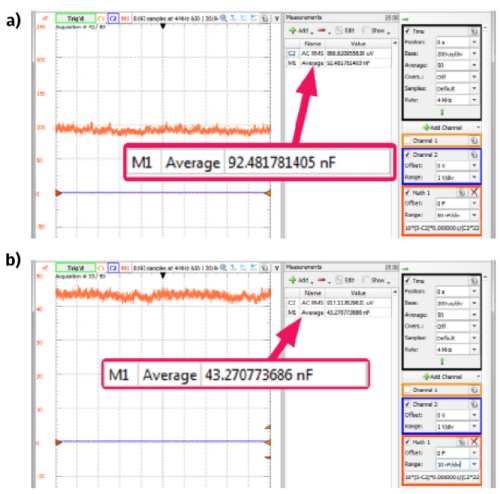
Teraz, gdy mostek jest już wyzerowany możemy przełączyć kabelek w pozycję „2”, co pozwoli zmierzyć prąd płynący przez potencjometr R_W, a następnie obliczyć jego rezystancję i na tej podstawie wyznaczyć pojemność badanego kondensatora. Musimy pamiętać o włączeniu źródła napięcia stałego ustawionego na 5 V. Zgodnie z obietnicą wprowadzamy też formułę, która pozwoli wyświetlić wynik bezpośrednio w jednostkach pojemności (w faradach). W tym celu klikamy prawym przyciskiem myszki w wolnym polu pod parametrami kanałów pomiarowych (rysunek 6). W wyświetlonym menu wybieramy opcję „Custom”. Pojawia się wówczas ramka „Math 1”, w której po kliknięciu na dolne pole wpisujemy wyznaczoną wcześniej formułę (4). Dla porządku ustalamy również jednostkę „F” (farad) w polu „Units” (rysunek 7). Pozostaje jeszcze zdefiniowanie pomiaru automatycznego, którym jest wartość średnia z kanału „Math 1”. W tak utworzonym polu będzie wyświetlana wartość mierzonej pojemności (rysunek 8). Na rysunku 9a pokazano rezultat pomiaru pierwszego kondensatora – ok. 92 nF, przy znamionowej pojemności 100 nF. Wynik całkiem poprawny, tym bardziej, że do obliczeń przyjęto znamionową pojemność kondensatora wzorcowego, a więc 100 nF, a nie jego rzeczywistą.

Rysunek 6. Uruchomienie okna, w którym wprowadzana jest formuła obliczeniowa

Rysunek 7. Okno wprowadzania formuły obliczeniowej

Rysunek 8. Definiowanie pomiaru automatycznego podającego pojemność mierzonego kondensatora

Teraz nie zmieniając kondensatora wzorcowego zmierzymy kondensator o znamionowej pojemności 47 nF. Powtarzamy dokładnie te same czynności. Okazuje się, że drugi kondensator ma pojemność ok. 43 nF (rysunek 9b). Wydaje się, że jest to też dość sensowna wartość, ale mimo to nie popadajmy w nadmierny optymizm. Zweryfikujmy teraz powyższe wyniki mierząc te same pojemności narzędziem Impedance dostępnym w Analog Discovery 2.

Rysunek 9. Tabela wyników pomiarów automatycznych zawierająca m.in. pojemność mierzonego kondensatora a) 100 nF, b) 47 nF

Pomiary pojemności narzędziem Impedance Analog Discovery 2

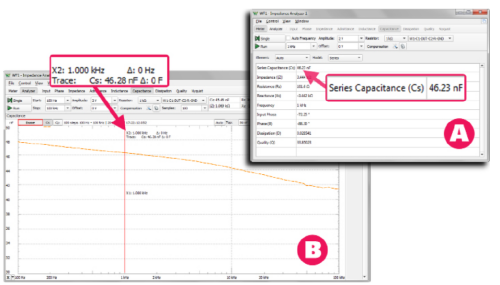
Impedance to narzędzie dodane do Waveforms 2015 jako jedno z ostatnich długo po premierze urządzenia, ale szybko okazało się, że jest ono bardzo przydatne w warsztacie elektronika. Jest przeznaczone do pomiaru niemal wszystkich parametrów impedancyjnych dwójników. Nie będziemy go teraz omawiać dokładnie, być może będzie jeszcze okazja do tego. Impedance użyjemy do szybkiego pomiaru pojemności kondensatorów, które wcześniej mierzyliśmy mostkiem. Do dyspozycji mamy dwa tryby pracy. W pierwszym z nich – „Meter” urządzenie mierzy parametry impedancyjne przy ustalonej częstotliwości. Pojemność kondensatora C_X (znamionowo 47 nF) zmierzona przy częstotliwości 1 kHz, a więc takiej samej jak w pomiarach mostkowych, była równa 46,23 nF (43,27 nF pomiar mostkiem) – rysunek 10a. Na tej podstawie można by przypuszczać, że pomiar mostkiem był jednak mniej dokładny, ale nie musi to być prawda, gdyż w pomiarach mostkowych przyjęliśmy pojemność znamionową kondensatora wzorcowego, a nie rzeczywistą.

Rysunek 10. Pomiar pojemności narzędziem Impedance Analog Discovery 2, a) w trybie "Meter", b) w trybie "Analyzer"

Na zakończenie pomiarów skorzystamy jeszcze z ciekawej cechy narzędzia Impedance, jaką jest pomiar parametrów elementów biernych w funkcji częstotliwości. Czasami wyniki mogą być bardzo zaskakujące. Szczególnie wtedy, gdy okaże się, że na przykład pojemność danego kondensatora dość drastycznie zmienia się w całym zakresie częstotliwości występujących w urządzeniu, w którym kondensator ma być zastosowany. Popatrzmy jak to jest w przypadku naszego kondensatora CX o znamionowej pojemności 47 nF. Już wiemy, że przy 1 kHz jest równa 46,23 nF (pomiar AD2). Wynik takiego pomiaru pokazano na rysunku 10b. Jak widać kondensator 47 nF ma rzeczywistą pojemność 47,7 nF przy 100 Hz i 40,7 nF przy 100 kHz.

Przydatność metody

Już na wstępie artykułu wyraziłem wątpliwość odnoszącą się do praktycznej przydatności przedstawionej metody pomiarowej. Ponieważ nie było przeciwwskazań teoretycznych postanowiłem ją sprawdzić i zaprezentować rezultaty. Uzyskane wyniki były dość sensowne, co mogłoby dawać nadzieję na praktyczną przydatność tej metody. Należałoby jednak przymknąć oko na dość złożone operacje manualne niezbędne do wykonania pomiaru.

Natomiast spory niepokój budzi złożona postać wyrażenia matematycznego, z którego wyznaczana jest pojemność mierzonego kondensatora. Sprawdźmy, jak bardzo uzasadnione są te obawy. Poniższy fragment artykułu zapewne zniechęci część Czytelników do dalszej lektury, tych wytrwałych zachęcam jednak do uważnego przeczytania ze zrozumieniem. W wyrażeniu, z którego jest wyznaczana pojemność kondensatora występuje aż 5 czynników mających wpływ na wynik końcowy. Oszacujmy więc, z jakim błędem powinniśmy się liczyć wykonując przedstawiony pomiar. Przyjmujemy więc, że formuła obliczeniowa jest funkcją 5 zmiennych (3), dla każdej z nich należy więc obliczyć pochodną cząstkową. Mamy zatem:

Przyjmujemy teraz, że poszczególne parametry wraz z tolerancjami są równe:
R_W = 10 Ω ±10%             U_CH2 = 49,5 mV ±5%               R4 = 2200 Ω ±10%
V+ = 5 V ±5%                 C_W = 100 nF ±20%
Całkowity błąd bezwzględny pomiaru pojemności kondensatora CX jest równy różniczce zupełnej:

Podstawiając przyjęte parametry do powyższego wyrażenia okazuje się, że błąd bezwzględny pomiaru C_X jest równy... ±22,8 nF (sic!), co w przypadku kondensatora 47 nF oznacza błąd względny 48%.

Weryfikacja metody pomiarowej w symulatorze LTspice

Właściwie powinniśmy taką symulację przeprowadzić na początku, aby sprawdzić czy zaproponowana metoda pomiarowa ma w ogóle jakiś sens. Pomiar na szczęście nie był bardzo skomplikowany, więc za dużo czasu nie straciliśmy.

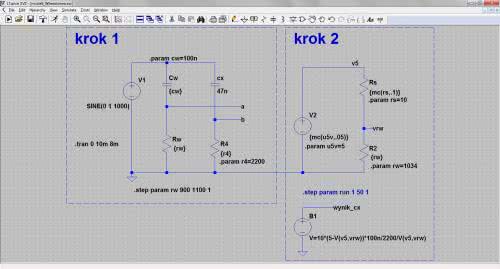
Schemat wirtualnego pomiaru pokazano na rysunku 11. Symulacja, tak jak pomiar rzeczywisty przebiega w dwóch etapach. W pierwszym kroku bazujemy na lewej części schematu opisanej „krok 1”. Wartości elementów są podane parametrycznie, wyjątkiem jest kondensator mierzony C_X o pojemności 47 nF. Kondensator wzorcowy CW ma pojemność 100 nF, a mostek jest zasilany napięciem sinusoidalnym o amplitudzie 3 V i częstotliwości 1000 Hz. Rezystor RW odpowiadający na tym schemacie potencjometrowi z pomiaru rzeczywistego ma parametrycznie zadaną rezystancję rw. Będzie ona krokowo zmieniana w trakcie symulacji komendą:
.step param rw 900 1100 1

Rysunek 11. Schemat układu pomiarowego w symulatorze LTspice

Oznacza to, że mostek będziemy równoważyć w zakresie zmian R_W od 900 do 1100 omów z krokiem 1 V. Aby wyeliminować ewentualne stany nieustalone po wirtualnym uruchomieniu układu podajemy wyniki ostatnich 2 milisekund analizy spośród 10, którymi objęta jest cała symulacja. Zapewnia to komenda:
.tran 0 10m 8m

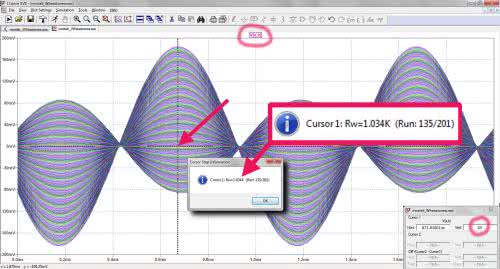
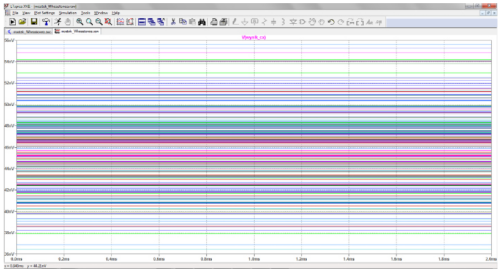
Symulacja rozpoczyna się po wydaniu polecenia Simulate → Run (ikona z grafiką biegacza). Zostaje wyświetlone puste okno, w którym będzie umieszczony wykres wskazanego przebiegu. Interesuje nas wyjście mostka, czyli punkty „a” i „b”. Naprowadzamy więc kursor na linię „a”, naciskamy prawy przycisk myszki i przytrzymując go przesuwamy kursor na linię „b”, po czym zwalniamy przycisk. W oknie wykresu pojawia się rodzina przebiegów (rysunek 12). Klikamy na tytuł wykresu („V(a,b)” nad wykresem), w wyniku czego pojawia się kursor pomiarowy i tabelka opisująca jego parametry. Teraz przesuwamy ten kursor tak, aby znalazł się nad jednym z maksimów wykresu i za pomocą przycisków „strzałka w górę”, „strzałka w dół” ustawiamy go do takiej pozycji, w której napięcie jest równe zero lub osiąga wartość jak najbliższą zeru. Po kliknięciu prawym przyciskiem na pionową kreskę kursora pomiarowego zostaje wyświetlone okno „Cursor Step Information”, z którego odczytujemy, że mostek został wyzerowany dla R_W=1034 Ω (rysunek 12). Poszło gładko, ale w ogólnym przypadku może się zdarzyć, że mostka nie uda się wyzerować. Należy wówczas zwiększyć zakres zmian RW kosztem wydłużenia czasu symulacji i zagęszczenia wykresu. Pamiętamy ponadto, że dla wartości elementów przyjętych w układzie, tzn. pojemności wzorcowej 100 nF, rezystancji R₄ równej 2200 V i całkowitej oporności potencjometru R_W=5 kΩ maksymalna pojemność mierzona, dla której uda się wyzerować mostek jest równa ok. 227 nF. Można to łatwo sprawdzić w symulacji lub obliczyć, do czego zachęcam już samodzielnie Czytelników.

Rysunek 12. Przebiegi wyświetlane w pierwszym kroku symulacji w LTspice

Wracamy do naszych pomiarów. Przechodzimy do kroku 2. Na wstępie należy zakomentować polecenie krokowej zmiany RW z 1. etapu i odkomentować polecenie:
.step param run 1 50 1

Oznacza ono uruchomienie kolejno następujących po sobie 50 symulacji, co będzie potrzebne do zgromadzenia danych dla pomiarów wykonywanych z zastosowaniem metody Monte Carlo. Polega ona na losowej zmianie wartości wskazanych parametrów w każdej kolejnej symulacji, a zatem zbadanie rozrzutu wyników, jakich można będzie spodziewać się w układzie fizycznym. Rezystor R_W powinien dokładnie odpowiadać rezystorowi R_W z kroku 1, więc musimy pamiętać o wprowadzeniu jego rezystancji 1034 Ω (.param rw=1034). Rozrzut wyników jest spowodowany rozrzutem takich parametrów, jak: rezystancja rezystora R_S i napięcie zasilające V2. Dlatego parametry te zapisujemy w postaci:
{mc(rs,.1)}
i
{mc(u5v,.05)}
oraz definiujemy rs i u5v:
.param rs=10
.param u5v=5

Powyższy zapis oznacza, że rezystor R_S będzie miał rezystancję 10 V z tolerancją ±10% (zapis .1). A napięcie zasilające będzie miało 5 V ±5%.

Dla zobrazowania wyników w postaci graficznej dość nietypowo użyjemy programowanego źródła napięciowego (Arbitrary behavioral voltage source), które w standardowej bibliotece elementów LTspice’a ma symbol „bv”. Ponieważ jest ono definiowane należy w polu „Value” w jego właściwościach wpisać formułę, którą stosowaliśmy w rzeczywistym układzie do obliczania pojemności mierzonej, a więc:
V=10·(5–V(v5,vrw))·100n/2200/V(v5,vrw)

Zwróćmy uwagę na to, że w wyrażeniu tym są zapisane znamionowe wartości elementów R_S i V2, a nie rzeczywiste. Zakres zmian zmierzonej pojemności C_X jest widoczny w oknie wykresu po kliknięciu na linię opisaną etykietą „wynik_cx”. Do zobrazowania użyto źródła napięciowego, więc oś pionowa jest opisana w woltach nie w faradach, na co przymykamy oko (rysunek 13).

Rysunek 13. Wyniki symulacji metodą Monte Carlo

Problem z Monte Carlo

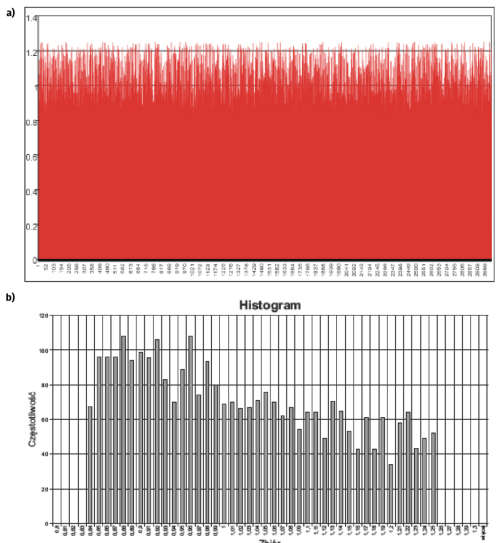
Metoda Monte Carlo to bardzo ciekawe narzędzie symulatora LTspice przewidziane do symulacji rozrzutu wybranych parametrów badanego układu wynikających np. z tolerancji. Wszystko było by dobrze, gdyby nie jedna ewidentna niedoróbka symulatora. Problem polega na tym, że program generuje wartości losowe z rozkładem... zbliżonym do równomiernego, ale też dalekim od ideału. Pozwoliłem sobie wykonać mały test. Wykonałem symulację z elementem o nominalnej wartości 1 i tolerancji 20%. Dla tego testu nie jest istotna fizyczna interpretacja elementu. Symulator wygenerował 3000 próbek. Proces ten pokazano na rysunku 14a. Widoczne są na nim wartości kolejno losowanych próbek. Następnie korzystając z możliwości Excela zbadałem rozkład wylosowanych wartości (rysunku 14b). Hmm... trudno nazwać go równomiernym, z całą pewnością nie jest to też rozkład normalny, któremu podlega rozrzut parametrów elementów fizycznych.

Rysunek 14. Badanie rozkładu liczb losowych generowanych komendą mc, a) wartości kolejnych próbek, b) rozkład generowanych liczb

Jest to temat, któremu warto się jeszcze przyjrzeć, co prawdopodobnie nastąpi w którymś z kolejnych odcinków. A w następnym temat bardziej „lajtowy”, po tym nieco przydługim. Zajmiemy się dopasowaniem mocy.

Jarosław Doliński, EP