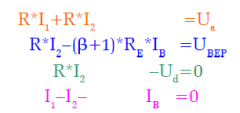Czy warto uczyć się matematyki, czyli projektowanie układów elektronicznych metodami inżynierskimi

Ogłoszone ostatnio w mediach wątpliwości NIK w zakresie sensu utrzymywania egzaminu maturalnego z matematyki zainspirowały mnie do refleksji na ten temat. Wątpliwości biorą się z obserwowanych ostatnio bardzo słabych wyników z tego egzaminu. Oczywiste jest, że nie każdy abiturient musi w przyszłości zostać inżynierem elektronikiem, więc po co przeciętnego ucznia dobijać egzaminem ze znienawidzonego przedmiotu nauczania? Wątpliwości wydają się więc zasadne. Mało tego, można zadać pytanie, czy w dzisiejszych czasach, w epoce komputerów i Internetu trzeba na blachę wykuwać metody rozwiązywania układów równań i uczyć się niezliczonej ilości praw i reguł. Przecież wystarczy tylko umiejętnie zadać pytanie wyszukiwarce i najdalej w ciągu kilkudziesięciu milisekund otrzymujemy setki, a nawet tysiące odpowiedzi. Inna sprawa, że nie wszystkie są poprawne, warto więc by było umieć ocenić ich przydatność. Tu odrobina wiedzy jednak się przydaje.

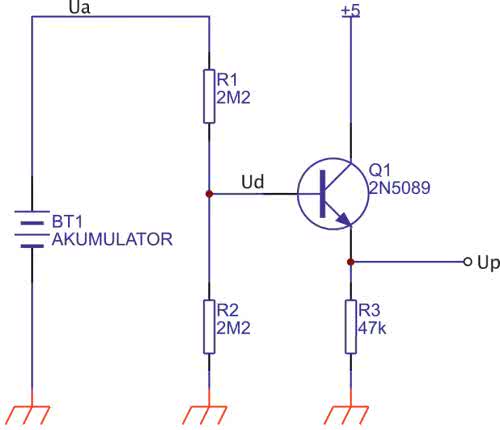
Wróćmy do obliczeń. Załóżmy, że projektujemy układ przedstawiony na rysunku 1. Będzie on wykorzystywany w systemie mikroprocesorowym do pomiaru napięcia akumulatora w celu podawania go użytkownikowi i ewentualnie reagowania na zbyt niski jego poziom. Obniżenie napięcia poniżej określonego progu może prowadzić do nieodwracalnego pogorszenia parametrów, a nawet uszkodzenia akumulatora. Warto więc takie zabezpieczenie stosować. Zasada działania jest banalna. Do akumulatora jest na stałe dołączony dzielnik napięciowy, do budowy którego użyto rezystorów o dużej rezystancji (2,2 MV). Prąd płynący przez dzielnik jest równy ok. 0,9 mA, jest więc pomijalnie mały z punktu widzenia żywotności akumulatora. Napięcie dzielnika jest mierzone przez przetwornik analogowo-cyfrowy procesora, a następnie przy użyciu odpowiedniej formuły zostaje przeliczone na napięcie akumulatora i na przykład wyświetlone na pulpicie operatora. Aby dzielnika nazbyt nie obciążać, zastosowano bufor w postaci wtórnika emiterowego. Najważniejszym zadaniem dla inżyniera jest sformułowanie wyrażenia matematycznego wykorzystywanego do przeliczenia napięcia Up zmierzonego przetwornikiem A/C procesora na odpowiadające mu napięcie akumulatora Ua.

Rysunek 1. Schemat ideowy projektowanego wskaźnika napięcia baterii

Niby prosty układ, ale już ma początku pojawia się kilka wątpliwości. Pierwszą z nich stanowi tranzystor bipolarny, a dokładniej jego złącze baza-emiter. Nie dość, że spowoduje ono obniżenie napięcia wyjściowego dzielnika o wartość napięcia przewodzenia UBEP, to jeszcze wprowadzi pewną nieliniowość. Pytanie czy istotną? Mimo zastosowania bufora, nadal nie mamy pewności czy dzielnik napięciowy nie będzie nadmiernie obciążony.

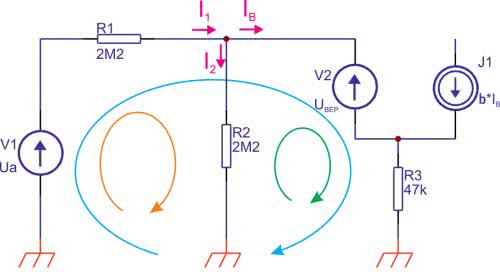
Przystępując do projektowania musimy rozważyć, czy zastosujemy metodę kartki i ołówka, czy raczej komputera i Internetu. A może połączymy obie te metody? Zacznijmy od policzenia stałoprądowego punktu pracy dla ustalonego napięcia akumulatora. Schemat zastępczy naszego układu maglowany na zajęciach z teorii obwodów przedstawiono na rysunku 2. Do policzenia mamy 4 niewiadome (właściwie 5, ale ta piąta jest dość oczywista). Są to: prądy I₁, I₂ i I_B oaz napięcie U_d, a w efekcie końcowym także napięcie U_p, które będzie mierzone przez procesor. Należy więc ułożyć układ 4 równań z 4 niewiadomymi i go rozwiązać. No i pojawia się pierwszy problem matematyczny.

Rysunek 2. Schemat zastępczy projektowanego układu wykorzystywany w obliczeniach

W szkole uczyli rozwiązywania co najwyżej układów 3 równań z 3 niewiadomymi. Na studiach ograniczenia tego już nie było, ale komu by się chciało za każdym razem analitycznie rozwiązywać takie zadanie? Chyba jednak skorzystamy z mocy Internetu. Tak czy inaczej układ trzeba jakoś ułożyć. Piszemy więc równania dla 3 oczek obwodu i jednego węzła (dla zwiększenia czytelności zaznaczonych kolorami). Pamiętamy, że zastosowaliśmy jednakowe wartości rezystorów dzielnika, którym nadajemy to samo oznaczenie (R). W obliczeniach korzystamy z zależności pomiędzy prądem emitera i prądem bazy tranzystora bipolarnego (I_E=I_B*(b+1)). Otrzymujemy układ równań:

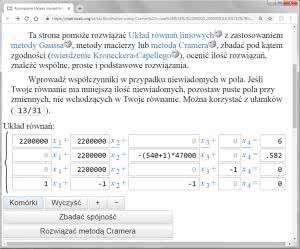
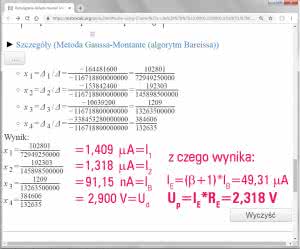
I znowu, układ niby prosty, ale leń nas jakiś jak większość inżynierów ogarnia, idziemy więc na łatwiznę i po kilku kliknięciach otrzymujemy na ekranie narzędzie do rozwiązania takiego układu on-line (http://bit.ly/2Hgl3M2). Narzędzie to nie daje jednak rozwiązań analitycznych, trzeba więc wstawić konkretne wartości dla jakiegoś stanu układu. Zakładamy więc, że napięcie akumulatora Ua=6 V, R=2,2 MV, _UBEP=0,582 V (dlaczego takie będzie wyjaśnione dalej), b=540. Po wprowadzeniu tych danych do specjalnego arkusza (rysunek 3) otrzymujemy rozwiązanie jak na rysunku 4, a więc I₁=1,409 mA, I₂=1,318 mA, I_B=91,15 nA, U_d=2,900 V i U_p=2,318 V.

Rysunek 3. Rozwiązywanie układu 4 równać z 4 niewiadomymi on-line

Rysunek 4. Wyniki obliczeń układu równań

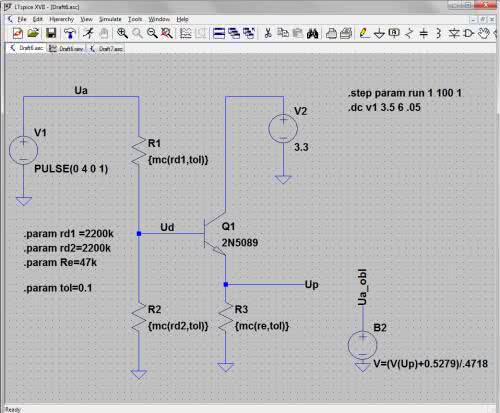
Załóżmy teraz, że napięcie akumulatora będzie się zmieniać liniowo w zakresie od 0 do 6 woltów. Podobnie liniowych zmian spodziewamy się na wyjściu pomiarowym (U_p). Możemy napisać, że napięcie w punkcie U_p będzie opisane zależnością U_p=a*U_a+b, w którym „a” jest współczynnikiem kierunkowym, a „b” przesunięciem charakterystyki spowodowanym obecnością napięcia złączowego UBEP przewodzącego tranzystora. Do znalezienia obu tych współczynników wykorzystamy symulator LTspice, bo dlaczego mamy sobie nie ułatwiać życia. Przy okazji zweryfikujemy obliczone wcześniej parametry. Schemat symulowanego układu przedstawiono na rysunku 5. Wykonujemy obliczenie „DC sweep” przyjmując zakres od 3,5 V do 6 V. Operacja ta umożliwia pomiar napięć i prądów DC w obwodzie w funkcji zmian wskazanego źródła wejściowego. Źródłem tym jest V1 odpowiadające naszemu akumulatorowi. Założono, że napięcie akumulatora nie powinno spadać poniżej 3,5 V, gdyż może to już powodować błędną pracę stabilizatora wytwarzającego napięcie 3,3 V zasilające elektronikę urządzenia.

Rysunek 5. Schemat układu symulowanego w programie LTspice

Rysunek 6. Uruchomienie kursorów na ekranie z wynikami pomiaru U_p=f(U_a)

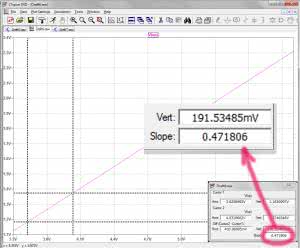
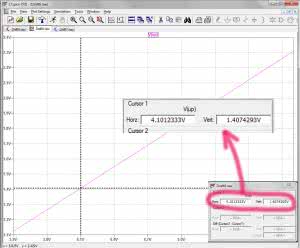
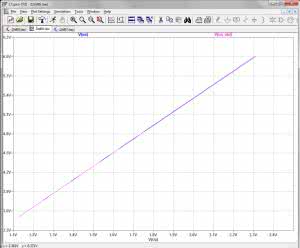
Po uruchomieniu symulacji komendą „Run” na ekranie pojawia się początkowo pusty wykres. Po ustawieniu kursora w punkcie U_p i kliknięciu lewym przyciskiem zostaje wyświetlony wykres zmian napięcia U_p w funkcji napięcia V1, a więc napięcia akumulatora (rysunek 6). Widać, ze jest to funkcja liniowa typu y=a*x+b (można w każdym razie z grubsza tak przyjąć). Z tego wykresu odczytamy współczynnik kierunkowy „a”. W tym celu wystarczy uruchomić dwa kursory, klikając prawym przyciskiem myszki na nagłówku wykresu. Zostaje wówczas wyświetlone menu, z którego wybieramy opcję „Atached Cursor→1st & 2nd”. Na ekranie pojawiają się dwa kursory, które należy rozsunąć pomiędzy dwa, w zasadzie dowolne miejsca wykresu (rysunek 7). Współczynnik kierunkowy odczytujemy bezpośrednio z okna parametrów kursorów, z pozycji „Slope”. W naszym wypadku a=0,4718, zatem równanie przybiera postać: U_p=0,4718*U_a+b. Pozostaje jeszcze obliczyć przesunięcie „b”. W tym celu mierzymy wirtualnie za pomocą kursora napięcie U_p dla jakiegoś napięcia U_a. Na przykład dla U_a=4,101 V, mamy U_p=1,407 V (rysunek 8). Przekształcając równanie prostej względem „b” dostajemy: b=U_p–0,4718*U_a. Zatem na podstawie powyższych wartości U_p i U_a otrzymujemy b=1,407–0,4718*4,101=–0,5217, a całe równanie wygląda tak:

U_p=0,4718*U_a–0,5279

Rysunek 7. Określenie współczynnika kierunkowego prostej U_p=a*U_a+b

Rysunek 8. Pomiar napięć Up i Ua w wybranym punkcie charakterystyki

Problem jest już prawie rozwiązany. Trochę elementarnej wiedzy na poziomie maturalnym jednak się przydało. Musimy jeszcze uporać się z jednym przekształceniem równania. Do napisania programu dla procesora potrzebna będzie zależność odwrotna. Naszym zadaniem jest przecież obliczenie napięcia akumulatora na podstawie zmierzonego napięcia z dzielnika, a nie odwrotnie. Ale to już jest wiedza na poziomie gimnazjalnym, więc liczymy:

U_a=(U_p+0,5279)/0,4718 Koniec. Takie równanie dajemy programiście i niech on męczy się dalej. Pozostaje jeszcze wytłumaczenie, dlaczego wzięliśmy do obliczeń napięcie U_BEP=0,582 V, a nie jak to często się przyjmuje 0,6 czy 0,7 V? Gdybyśmy tak postąpili pewnie wielkiego błędu byśmy nie popełnili, ale dlaczego nie skorzystać z dostępnego, bezpłatnego narzędzia, jakim jest LTspice?

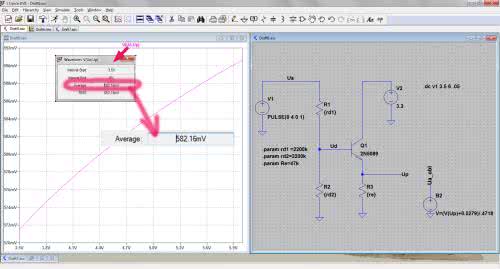
Po uruchomieniu symulacji, tak jak poprzednio, nie obserwujemy napięcia U_p, gdyż tym razem chcemy sprawdzić jak będzie się zmieniało napięcie baza-emmiter tranzystora. Dlatego nie wskazujemy jednego punktu na schemacie, a po kliknięciu na bazę tranzystora przeciągamy kursor do emitera przytrzymując wciśnięty lewy przycisk myszki. Zwalniamy go dopiero po najechaniu na emiter. W ten sposób uzyskujemy na ekranie wykres napięcia U_BEP w funkcji napięcia akumulatora w interesującym nas zakresie, a więc od 3,5 do 6 V (rysunek 9). Widoczna jest już wyraźnie nieliniowość, ale praca nad jej implementacją byłaby chyba w naszym projekcie przerostem formy nad treścią. Obliczamy więc wartość średnią napięcia U_BEP i tą przyjmujemy do obliczeń. Łatwo powiedzieć, ale jak to zrobić. No nie, matematykę odstawmy na razie na bok, średnią wyliczy program. Wystarczy najechać kursorem na tytuł wykresu i przy naciśniętym przycisku Ctrl na klawiaturze komputera nacisnąć lewy przycisk myszki. W wyniku takiego działania na ekranie zostanie wyświetlone okienko z kilkoma parametrami, wśród których jest wartość średnia mierzonego napięcia (Average).

Rysunek 9. Pomiar średniego napięcia UBEP w przyjętym zakresie pracy

Weryfikacja

Pozostaje jeszcze jakoś upewnić się, czy równanie, które przekazujemy programiście jest poprawne. Jeśliby nie było, zapewne na długo stalibyśmy się obiektem do drwin i wyśmiewania. Weryfikacja może wyglądać tak, że ponownie wykonujmy symulację jak poprzednio, z tym że nieco inaczej konfigurujemy wykres. Pamiętamy przecież, że interesuje nas (i programistę) zależność U_a=f(U_p), a nie odwrotnie. Musimy więc zamienić miejscami osie.

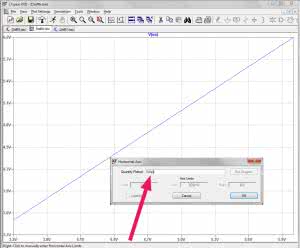
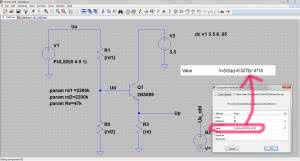
Na osi odciętych (maturzyści wiedzą o czym mowa) będzie odkładane napięcie U_p, a na osi rzędnych napięcie U_a. Ustawiamy więc kursor na opisie liczbowym dolnej osi. Powinien zamienić się on na małą linijkę. Klikamy prawym przyciskiem myszki, co powoduje wyświetlenie okna „Horizontal Axis” (rysunek 10). W polu „Quantity Plotted” wpisujemy V(U_p) i naciskamy przycisk ekranowy „OK”. Do ustawienia parametru mierzonego na osi pionowej wystarczy kliknąć myszką na schemacie na linii U_a. Na ekranie został pokazany interesujący nas wykres U_a=f(U_p), ale na razie nic z niego nie wynika. Aby sprawdzić poprawność wyznaczenia równania (tego, które przekazujemy programiście) wprowadzamy na schemacie napięciowe źródło „Arbitrary behavioral” (ozn. bv – rysunek 11). Umożliwi ono wyświetlenie zdefiniowanej przez nas niemal dowolnej zależności matematycznej. W polu „Value” w oknie właściwości tego źródła wprowadzamy oczywiście skrzętnie wyliczone równanie (rysunek 12) i ponownie uruchamiamy symulację. Do pełni szczęścia pozostaje jeszcze porównanie wykresu U_a=f(U_p) z wykresem jaki otrzymałby programista w uruchamianym przez siebie oprogramowaniu. Jeśli zaufamy naszemu symulatorowi, to wystarczy nałożyć na siebie wykresy U_a=f(U_p) i U_{a_ob}l=f(U_p). Pierwszy wykres już mamy na ekranie, trzeba jeszcze dorzucić drugi. Klikamy więc na dołożone źródło bv, którego wyprowadzenie oznaczyliśmy etykietą U_{a_obl} i czekamy na efekt (rysunek 13). Wow! Chciałoby się krzyknąć. Wykresy niemal idealnie pokrywają się ze sobą. Wykonaliśmy kawał dobrej roboty. Rodzi się jednak pewna wątpliwość…

Rysunek 10. Zmiana konfiguracji układu współrzędnych na wykresie

Rysunek 11. Wprowadzenie arbitralnego źródła napięciowego

Rysunek 12. Okno definiowania funkcji napięciowego źródła arbitralnego

Rysunek 13. Porównanie charakterystyki zmierzonej i obliczonej

Tolerancja

Jak wynika z symulacji weryfikującej, obliczenia zostały wykonane bardzo dokładnie i można spodziewać się poprawnego działania układu już w świecie rzeczywistym, a nie tylko wirtualnym. Jednak do budowy urządzenia będą wykorzystywane, na przykład, oporniki niewiadomego pochodzenia, a ich znamionowa rezystancja nie będzie tak idealna, jak rezystancja oporników w programie Spice. Intuicyjnie wyczuwamy zagrożenie, i to wcale niemałe. Warto więc upewnić się, jaki wpływ na pracę układu będzie miała, na przykład, tolerancja rezystancji zastosowanych oporników.

Tolerancja wyznacza nam gwarantowany przez producenta przedział parametrów tych elementów. Jeśli weźmiemy ich garść, to zapewne okaże się, że każdy opornik będzie miał inną rezystancję mieszczącą się jednak w przedziale wyznaczonym tolerancją. Na nieszczęście, w ogólnym przypadku, szczególnie wtedy, gdy w danym urządzeniu użyto dużej liczby elementów, trudno jest bez głębszej analizy ustalić, czy krytyczne są odchyłki w dół, czy w górę od wartości znamionowych. Co gorsza, dla jednych elementów bardziej niekorzystne z punktu widzenia parametrów całego urządzenia będą odchyłki w dół, a dla innych w górę. Teoretycznie można by poprzyjmować tylko graniczne wartości poszczególnych elementów i sprawdzić dla nich parametry całego urządzenia. Ze względu jednak na wspomnianą już trudność określenia, który parametr jest bardziej niekorzystny, który mniej oraz ze względu na dużą liczbę możliwych kombinacji, metoda taka mogłaby nie dać poprawnej oceny.

Monte Carlo znane nie tylko z rajdu samochodowego

Pomocna w takiej sytuacji może okazać się metoda o wdzięcznej nazwie Monte Carlo, znana już z czasów pierwszego komputera – ENIAC’a, a więc z lat 1945-1946. Polega ona na wielokrotnym powtarzaniu symulacji z losowo i niezależnie zmienianymi parametrami elementów biorących udział w obliczeniach. Tym samym, przy wystarczająco dużej liczbie powtórzeń powstaje pole wyników pokrywające wszystkie możliwe wartości i kombinacje parametrów. Na tej podstawie znacznie łatwiej jest oceniać poprawność działania urządzenia.

Opis

Powróćmy więc do naszego wskaźnika. Załóżmy, że do jego budowy używamy popularnych i tanich rezystorów o tolerancji 10%. Nasz programista prawdopodobnie bezkrytycznie podszedł do zagadnienia i wierząc naszej wyliczonej formule, nie wnikając w szczegóły odczytuje napięcie z ADC i przelicza je na napięcie akumulatora. Podaje jedną konkretną wartość przy założeniu znamionowych rezystancji wszystkich oporników. Okazuje się jednak, że podane przez niego napięcie mniej lub bardziej różni się od rzeczywistego. Pytanie jak bardzo?

Do oszacowania różnicy ponownie zaprzęgniemy Ltspice. Wartości elementów będą podawane parametrycznie, przy czym zostanie zastosowana funkcja mc losująca te wartości w zadanym zakresie wokół wartości znamionowej. LTspiceowy generator pseudolosowy ma wadę polegająca na tym, ze generowane przez niego liczby losowe mają rozkład równomierny, gdy tymczasem rozrzut rezystancji oporników ma rozkład gaussowski. Nie jest to jednak wada wykluczająca stosowanie tego narzędzia. Parametrem funkcji mc są: wartość nominalna (środkowa) i tolerancja plus/minus. Przykładowo, użyte w urządzeniu rezystory dzielnika mają rezystancję znamionową 2,2 MV i tolerancję ±10%, ich wartość jest więc opisaną formułą: {mc(2200k,0.1)}. Zapis ten należy rozumieć tak, że w każdym kolejnym przebiegu symulacji dla każdego tak opisanego rezystora zostanie wylosowana liczba z zakresu 2200000 ±220000 czyli od 1980000 do 2420000 i będzie ona traktowana jako jego rezystancja. Schemat ideowy pozostaje niemal taki sam, zmieniają się jedynie wartości rezystorów (rysunek 14). Wprowadzono ponadto zmienną „tol” określającą tolerancję rezystancji. Do uruchomienia symulacji potrzebna jest jeszcze trochę nietypowa komenda:

.step param run 1 100 1

Rysunek 14. Zmodyfikowany schemat dla symulacji metodą Monte Carlo

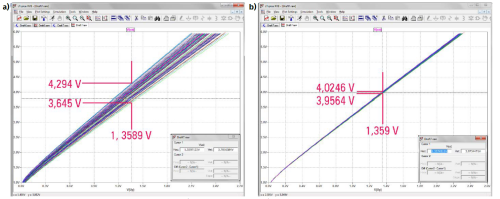
Wszystkie przebiegi symulacji mają nadawane numery. Wynika stąd konieczność podawania ich zakresu oraz kroku inkrementacji. W naszym przypadku wykonujemy 100 przebiegów symulacji (od 1 do 100). Zakres analizy pozostaje taki sam jak w poprzedniej symulacji, a więc napięcie źródła V1 (czyli napięcie akumulatora) zmienia się od 3,5 do 6 V. Uzyskany wykres potwierdza nasze wcześniejsze obawy (rysunek 15a). Przykładowo, napięciu zmierzonemu przez przetwornik A/C równemu 1,359 V odpowiada w układzie idealnym napięcie akumulatora równe 4 V. W układzie z rezystorami 10-procentowymi przy tym samym napięciu zmierzonym przez przetwornik A/C należy liczyć się ze zmianami Ua w zakresie od 3,645 V do 4,294 V. Teraz chciałoby się zawyć z rozpaczy. To stanowczo za dużo. To praktycznie dyskwalifikacja takiego rozwiązania. Zobaczmy na ile poprawią układ rezystory 1-procentowe.

Rysunek 15. Wyniki symulacji metodą Monte Carlo a) dla rezystorów 10%, b) dla rezystora 1%

Zmieniamy zatem wartość parametru „tol” na 0.01 i ponawiamy symulację. Wyniki przedstawiono na rysunku 15b. I ponownie odetchnęliśmy z ulgą. Wynik jest bardzo satysfakcjonujący. Tym razem napięcie, które według obliczeń powinno być równe 4 V w rzeczywistości zmienia się w zakresie od 3,9564 V do 4,0246 V. Rewelacja.

Czy „apteka” jest potrzebna w obliczeniach inżynierskich?

To jest pytanie, które często inżynierowie zadają sobie samym. Z jednej strony, im większa będzie precyzja obliczeń, tym większa będzie szansa dokładniejszego oddania rzeczywistości w tworzonym modelu matematycznym. Innym argumentem jest efekt kumulacji błędów obliczeniowych prowadzący do znacznego błędu końcowego. Z drugiej jednak strony powyższy przykład pokazał, że nadmierna precyzja obliczeń nie ma większego sensu, gdyż naturalny rozrzut parametrów elementów użytych do budowy urządzenia powoduje i tak wypaczenie oczekiwanych wyników. Wydaje się, że w obliczeniach inżynierskich dokładność do trzech cyfr znaczących powinna być wystarczająca. W czasach suwaków logarytmicznych nawet taka dokładność była dość trudna do osiągnięcia, a mimo to mosty budowane wtedy stoją do dziś.

Chciałem w tym artykule pokazać, że wiedza matematyczna jednak do czegoś się przydaje i nie warto rezygnować z egzaminu z matematyki na maturze. Chyba nie do końca mi się to udało, gdyż większość obliczeń w opisywanym projekcie wykonał komputer, ale ktoś te komputery musi jednak programować.

Jarosław Doliński, EP