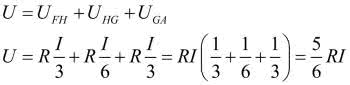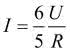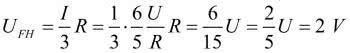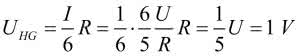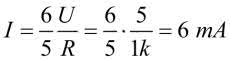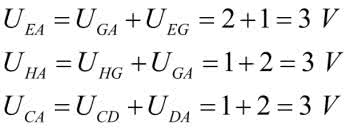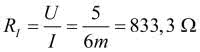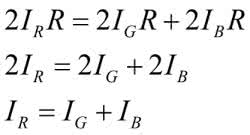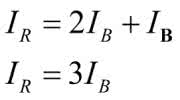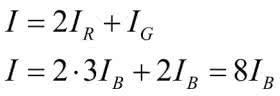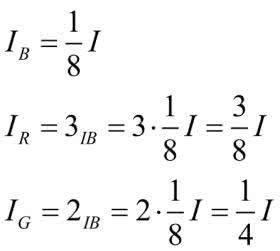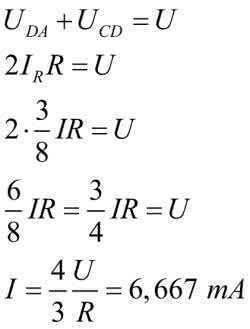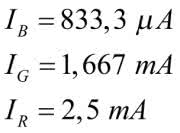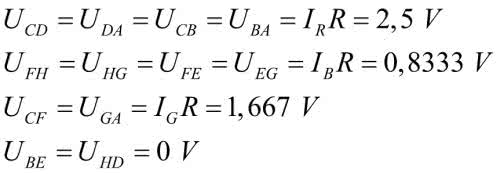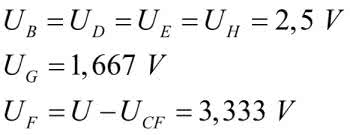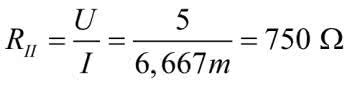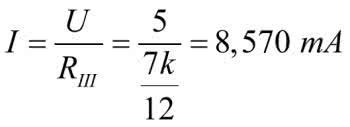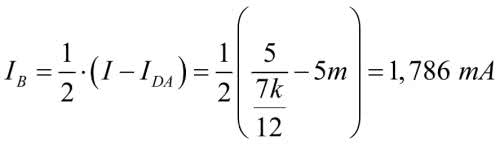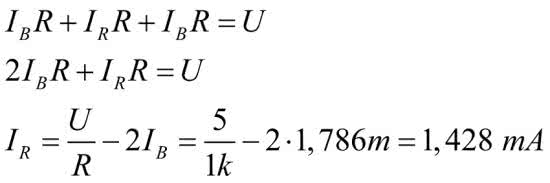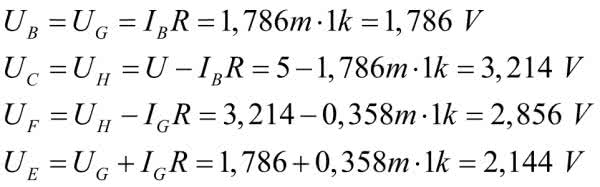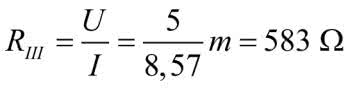Problem, o którym mowa w artykule, jest typowo akademicki. Zadania, które rozwiążemy dalej, pojawiały się na różnych egzaminach i testach szkół i uczelni technicznych. Z pozoru problem wydaje się dość trudny, przede wszystkim z powodu skomplikowanej sieci połączeń mającej wiele rozwidleń.
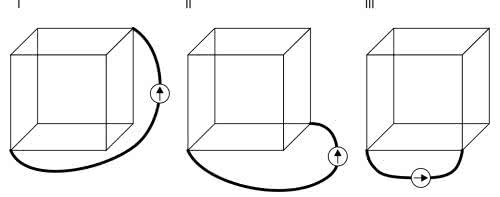
Mamy więc kostkę zbudowaną z rezystorów o jednakowej rezystancji (rysunek 1). Dla ustalenia niech to będzie 1 kΩ. Do kostki doprowadzone jest napięcie stałe, np. 5 V. Ze względu na symetrię kostki można wyróżnić 3 warianty dołączenia zasilania (rysunek 2).
Rozpatrzymy każdy z nich. Najpierw wykonamy obliczenia, następnie sprawdzimy ich poprawność w symulatorze i tradycyjnie na koniec zbudujemy taką kostkę i ją pomierzymy.
Kostka – wariant I
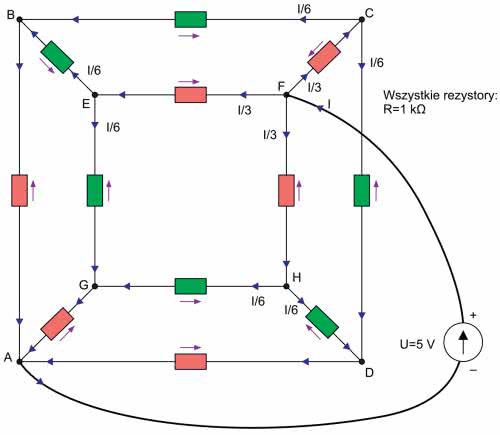
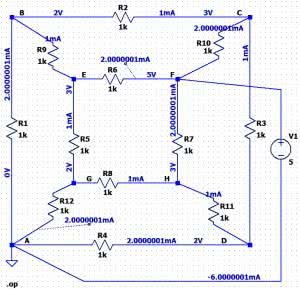
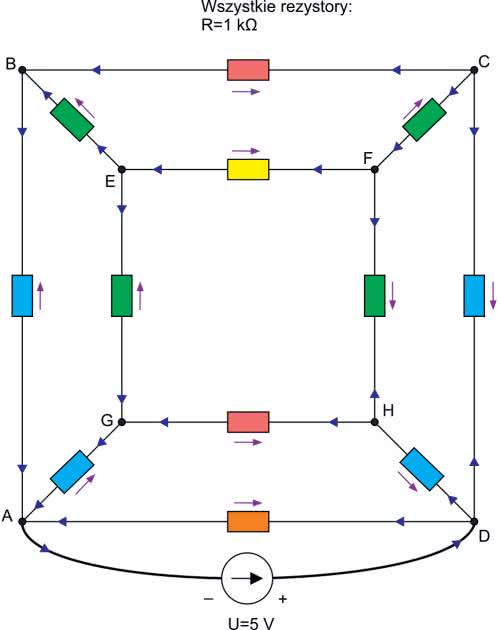
W pierwszym wariancie zasilanie jest doprowadzone do wierzchołków znajdujących się na końcach wewnętrznej przekątnej kostki. Przestrzenny widok kostki z rysunku 1 nieco spłaszczymy (rysunek 3), co powinno zwiększyć czytelność schematu, a przy odrobinie wyobraźni nadal będzie to rysunek przestrzenny.
I tak – większy kwadrat ABCD niech będzie ścianką leżącą bliżej nas, ten mniejszy natomiast EFHG to ścianka leżąca w głębi. Zgodnie z założeniem zasilanie jest doprowadzone do węzłów A i F. Nasze zadanie jest ułatwione dzięki przyjętemu założeniu, że wszystkie rezystory kostki są jednakowe. Jeśli więc przyjrzymy się kostce w tej konfiguracji, to z pewnością dostrzeżemy, że układ połączeń jest symetryczny. W związku z tym w węźle F, do którego jest dołączony dodatni biegun zasilania, prąd rozpływa się na 3 jednakowe prądy stanowiące 1/3 prądu całkowitego (płynącego z zasilania). Rezystory, przez które przepływa prąd o tym natężeniu, wyróżniono na schemacie kolorem czerwonym. Analizując dalszą drogę przepływu tego prądu, dochodzimy do punktów E, C i H, w których prąd rozpływa się na kolejne dwa równe prądy o natężeniach: I/2·I/3=I/6. I znowu, w kolejnych węzłach B, D i G spotykają się dwa takie prądy dopływające do nich, wypływa natomiast jeden prąd stanowiący ich sumę, a więc I/3. Prądy o natężeniach I/3 sumują się w węźle A, z którego wypływają do źródła jako prąd o natężeniu I. Proste, prawda?
Prześledźmy teraz rozkład napięć na drodze +źródła zasilającego, F, H, G, A –źródła zasilającego:
z czego wynika, że prąd całkowity jest równy:
Obliczamy teraz kolejne napięcia:
Takie napięcie będzie występowało na wszystkich czerwonych rezystorach. Biegunowość tych napięć zaznaczono na schemacie strzałkami. Trzymając się konwencji, że pierwszy indeks oznacza punkt o wyższym potencjale, możemy napisać:
Analogiczne rozważanie przeprowadzimy dla rezystorów zielonych, przez które płynie prąd I/6.
Wynika z tego, że:
Policzmy teraz prądy. Prąd całkowity płynący ze źródła:
Prądy płynące przez czerwone rezystory są równe I/3, a więc 6 m/3=2 mA. Ostatecznie:
Prądy płynące przez zielone rezystory są równe I/6, z więc 6m/6=1 mA. Ostatecznie:
Inżynierska poprawność nakazuje jeszcze obliczenie napięć we wszystkich węzłach kostki mierzonych względem masy, czyli punktu A. Mamy już policzone napięcia:
Pozostają jeszcze do obliczenia poniższe napięcia:
Warto jeszcze obliczyć rezystancję widzianą z węzłów, do których jest doprowadzone zasilanie. Rezystancja ta jest równa:
Symulacja kostki w wariancie połączeń nr I
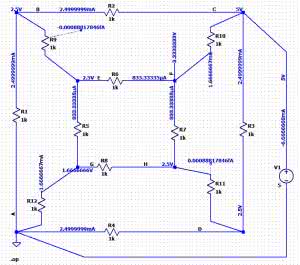
Kostkę rozrysowaną w edytorze LTspice pokazano na rysunku 4.
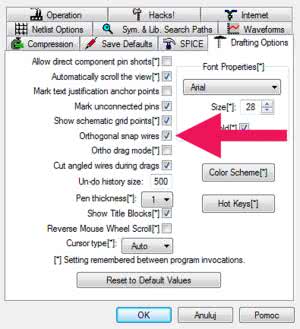
Wyjaśnienia wymagają ukośne połączenia na tym schemacie. Standardowo LTspice zakłada prowadzenie połączeń tylko w kierunkach prostopadłych do siebie, czyli pionowo i poziomo. Zasadę tę można lokalnie wyłączyć, naciskając przycisk Ctrl podczas prowadzenia połączenia. Połączenie jest wówczas prowadzone bez zachowania ortogonalności, jednak zawsze musi być ono zakończone w węźle siatki. Zasada ta zapewnia utrzymywanie ciągłości połączeń. Drugą metodą jest trwałe wyłączenie ortogonalności połączeń. W tym celu należy otworzyć okno parametrów domyślnych symulatora (ikonka z młotkiem), a następnie wybrać zakładkę „Drafting Options” i odhaczyć opcję „Orthogonal snap wires” (rysunek 5). Od tej chwili połączenia są prowadzone bez pilnowania ich otrogonalności, a naciśnięcie przycisku Ctrl przywraca chwilowo tę zasadę.
O ile połączenia mogą być prowadzone pod dowolnym kątem (tzn. takim, który wynika z zakończenia połączeń w punktach siatki), o tyle elementy mogą być obracane tylko o ±90° lub 180°. Gdyby tak nie było, końcowy punkt wyprowadzenia elementu mógłby znaleźć się pomiędzy węzłami siatki i wówczas nie byłoby możliwe doprowadzenie do niego połączenia z innymi elementami.
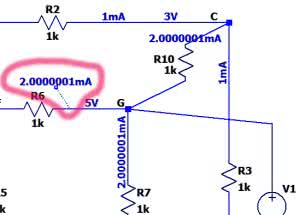
Do weryfikacji naszych wyników konieczne jest wykonanie symulacji .op (DC operating point). Kończy się ona wyświetleniem tabelki, w której zebrano wszystkie napięcia i prądy występujące w obwodzie. Taka analiza jest jednak dość niewygodna, znacznie lepiej jest nanieść te wartości bezpośrednio na schemacie. Do umieszczenia napięć węzłowych wystarczy po zakończeniu symulacji .op kliknąć na jakiś punkt leżący na połączeniu prowadzącym do danego węzła. Nieco więcej czynności wymaga umieszczenia prądu płynącego w danej gałęzi.
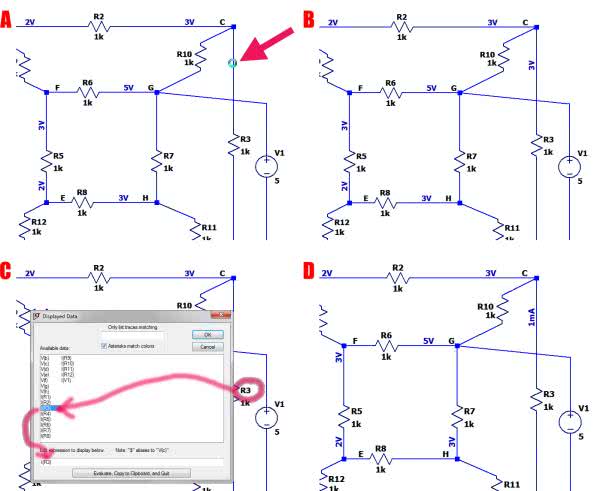
Przykładowo: chcemy umieścić na schemacie natężenie prądu płynącego w gałęzi z rezystorem R3. W tym celu wyświetlamy najpierw napięcie w jakimś punkcie tej gałęzi, klikając na niej lewym przyciskiem myszki (rysunek 6a). Na schemacie zostaje umieszczone napięcie we wskazanym punkcie (rysunek 6b). Następnie poddajemy wyświetloną wartość edycji, klikając na nią tym razem prawym przyciskiem, co powoduje wyświetlenie okna „Displayed Data” (rysunek 6c). Ponieważ chcemy wyświetlić prąd płynący przez rezystor R3, wyszukujemy w wyświetlonych danych prądu I(R3) i dwukrotnym kliknięciem wprowadzamy ten prąd do pola „Edit expression to display below”. Należy pamiętać o wcześniejszym usunięciu znaku dolara, który domyślnie jest tu wyświetlany. Na koniec naciskamy przycisk OK, co powoduje umieszczenie natężenia prądu na schemacie (rysunek 6d). Może się zdarzyć, że na schemacie nie ma już miejsca na umieszczenie kolejnej informacji. Dobrą rozwiązaniem jest odsunięcie informacji o prądzie w dogodne miejsce i wskazanie gałęzi, do której się ona odnosi, linią rysunkową („Edit → Draw → Line”) – rysunek 7.
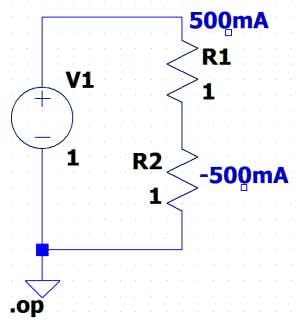
Jest jednak jeszcze cecha programu LTspice, o której należy pamiętać. Może się zdarzyć, że niektóre prądy płynące w jednej gałęzi zostaną wyświetlone jako dodatnie, inne zaś będą ujemne. LTspice przyjmuje kierunek prądu płynącego przez rezystor od jego wyprowadzenia 1. do 2. Jeśli symbol rezystora przed umieszczeniem go na schemacie był obracany, to w niekorzystnym przypadku prąd płynący przez niego może być podany ze znakiem ujemnym.
Taki przykład przedstawiono na rysunku 8, na którym rezystor R2 przed ostatecznym umieszczeniem go na schemacie był dwukrotnie obrócony. Prowadzi to do dość paradoksalnej sytuacji, z której mogłoby wynikać, że w obwodzie w tej samej gałęzi płynie prąd w przeciwnych kierunkach.
Kostka – wariant II
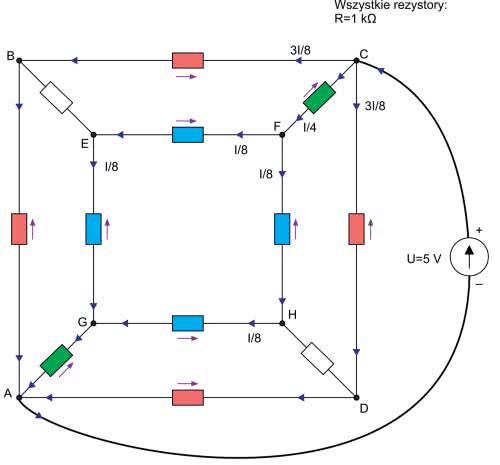
Kostka w tej konfiguracji jest znacznie ciekawsza, gdyż występuje w niej efekt, którego na pierwszy rzut oka nie widać i nawet trudno go intuicyjnie zaakceptować. Schemat połączeń pokazano na rysunku 9.
Układ nie jest w pełni symetryczny. Prąd może przepływać od węzła C do węzła A kilkoma niejednakowymi drogami. Na przykład może to być droga CDA albo CFHGA. W pierwszym przypadku prąd przepływa przez dwa rezystory, w drugim przez cztery. Wniosek jest taki, że w węźle C prąd nie rozpływa się na 3 równe prądy, tak jak to było w poprzedniej konfiguracji. Przyjrzyjmy się, jak to będzie w węźle F. Od węzła F do węzła A zawsze prowadzi droga przez 3 rezystory (FEGA lub FHGA, ale też FEBA lub FHDA), a więc prąd płynący w gałęzi CF rozpłynie się w węźle F na dwa równe prądy. I teraz najciekawsze. Zauważmy, że kostka jest symetryczna względem przekątnej BD, z czego wynika wniosek, że potencjały w punktach B, E, H i D muszą być równe, a jeśli tak, to... w gałęziach BE i DH nie płynie żaden prąd (sic!). Jesteśmy więc bliscy rozwiązania. Rezystory, przez które przepływają te same prądy, oznaczymy na schemacie tymi samymi kolorami. Policzmy te prądy. Zastosujemy oznaczenia: IR – prąd płynący przez rezystory czerwone, IG – prąd płynący przez rezystory zielone i IB – prąd płynący przez rezystory niebieskie. Zaczynamy od spadków napięć na drodze CDA.
Na drodze CFHGA mamy:
Zatem:
Ale IG=2IB, więc:
Prąd całkowity płynący ze źródła jest równy:
Ostatecznie:
Teraz można już policzyć prąd całkowity.
Dla przyjętych wartości (U=5 V, R=1 kΩ) prąd całkowity jest równy 6,67 mA i dalej:
Obliczenia napięć:
Napięcia mierzone względem masy (punkt A):
Rezystancja kostki jest w tej konfiguracji równa:
Symulacja kostki w wariancie połączeń nr II
Schemat kostki narysowany w edytorze symulatora pokazano na rysunku 10.
Uruchamiamy symulację poleceniem .op i natychmiast zostają wyświetlone wyniki. Szybka ich analiza potwierdza prawidłowość obliczeń. Jest tylko małe „ale”. W gałęziach, przez które miał nie płynąć prąd, symulator jednak coś wykrył. Obliczył, że popłynie prąd o natężeniu 0,000888 fA (femtoamperów), czyli 8,888·10-19. Jest to oczywiście błąd obliczeniowy wynikający z zaokrągleń, którym nie należy się przejmować.
Kostka – wariant III
Tym razem kostkę przeanalizujemy inną metodą. W poprzedniej konieczna była intuicja i umiejętność wynajdywania pewnych własności układu. Metoda, którą zastosujemy teraz, jest stricte techniczna, trzeba tylko się pilnować, żeby nie popełnić jakiegoś błędu obliczeniowego.
Jak widać na rozrysowanym schemacie kostki (rysunek 11), występuje w niej sporo oczek i węzłów. Stosowanie na przykład metody oczkowej prowadziłoby do konieczności rozwiązania dość złożonego układu równań z wieloma niewiadomymi. W zasadzie, w sytuacji gdy dostępne są różne programy komputerowe służące do takich obliczeń, nie jest to wielka trudność, ale można ten problem rozwiązać względnie łatwo inaczej. Do obliczeń zastosujemy metodę przekształceń obwodów trójkąt w gwiazdę i gwiazda w trójkąt.
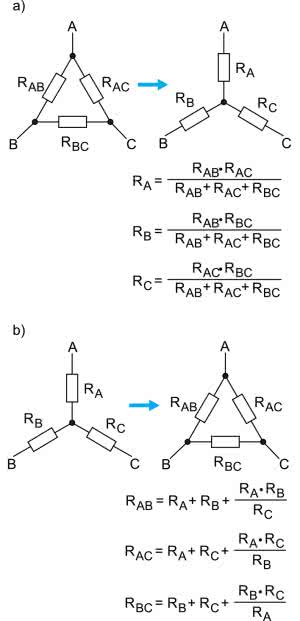
Oba przypadki pokazano na rysunku 12. Na rysunku 12a mamy połączenie w układzie trójkąta, które przekształcimy w gwiazdę. Przekształcony obwód jest pod względem elektrycznym dokładnym odpowiednikiem konfiguracji pierwotnej, tzn. w węzłach A, B i C obu obwodów występują takie same napięcia. Również prądy wpływające do nich są identyczne.
Na rysunku 12b mamy sytuację odwrotną, tzn. obwód w konfiguracji gwiazdy przekształcamy w trójkąt. Potrzebne do tego wzory podano na rysunku 12b. Wzory przyjmujemy na wiarę. Ich wyprowadzenie, chociaż nie jest trudne, wykracza poza temat artykułu.
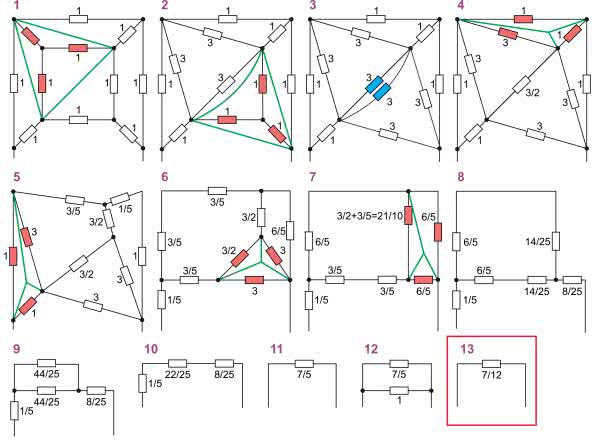
Naszą kostkę będziemy w kolejnych krokach zwijać, aż do uzyskania jednego rezystora, który pozwoli obliczyć prąd pobierany ze źródła i rezystancję kostki. Dla uproszczenia obliczeń zakładamy, że wszystkie rezystory mają rezystancję 1 Ω. Kolejne etapy zwijania przedstawiono na rysunku 13.
Przyjmiemy konwencję taką, że elementy brane do przekształcenia w danym kroku są zaznaczane na czerwono, a zieloną linią zaznaczamy konfigurację po przekształceniu w tym kroku. Na następnym rysunku przekształcone elementy są już rysowane normalnie. Tym razem obliczenia nie będą zamieszczane w tekście, a wyniki są podane bezpośrednio na rysunku. W kroku 3. rezystory są zaznaczone kolorem niebieskim, gdyż obliczana jest tylko rezystancja zastępcza dwóch rezystorów połączonych równolegle. We wszystkich krokach wykonujemy obliczenia na ułamkach całkowitych, czego niestety nie potrafi LTspice.
Miejmy nadzieję, że w końcowym wyniku nie wystąpią znowu jakieś femtoampery.
Dodatkowym uproszczeniem będzie pominięcie dolnego rezystora, który jest dołączony bezpośrednio do źródła zasilającego. Uwzględnimy go dopiero w ostatnim kroku obliczeń. To chyba wszystkie uwagi dotyczące obliczeń, przenosimy więc wzrok na rysunek 13.
W kroku 11. otrzymaliśmy oporność zastępczą kostki, ale bez dolnego rezystora, który dorysowujemy w kroku 12. Ostatecznie pełna kostka widziana od strony zasilania ma rezystancję RIII=7/12=0,583 kΩ.
Zastosowana metoda pozwoliła obliczyć rezystancję widzianą w wybranych dwóch punktach, w tym przypadku od strony zasilania. Aby policzyć prądy i napięcia w innych punktach należałoby przeprowadzić podobny tok obliczeniowy, tak aby zakończyć rozważania na tych właśnie punktach. Okazuje się, że wówczas jest to jednak metoda dość uciążliwa. Popatrzmy jeszcze raz na rozrysowaną kostkę z rysunku 11. Prąd płynący z zasilania na drodze DHGA i na drodze DCBA wytwarza spadki napięć na takiej samej liczbie rezystorów, zatem prądy płynące w gałęziach DH i DC muszą być równe. Oznacza to, że prąd płynący ze źródła pomniejszony o prąd gałęzi DA dzieli się na dwie równe części. Obliczamy:
Przez rezystor gałęzi DA płynie prąd 5/5k=5 mA, więc prąd
Mając prąd IB, łatwo możemy policzyć prąd IR płynący przez czerwony rezystor. Korzystamy z równania opisującego spadki napięć w gałęzi ABCD:
Z rozpływu prądu np. w węźle C mamy:
Prąd IG, jest więc równy:
Mając prąd IG można obliczyć ostatni prąd IY. Jest on równy:
Pozostał już ostatni etap – obliczenie napięć węzłowych.
Mamy komplet wyników. Napięcia międzywęzłowe można obliczyć z odpowiednich różnic napięć węzłowych. Pozostało jeszcze obliczenie rezystancji:
Symulacja kostki w wariancie połączeń nr III
Schemat kostki wraz z wynikami symulacji .op pokazano na rysunku 14.
Wyniki zgadzają się z inżynierską dokładnością, można więc z czystym sumieniem uznać, że obliczenia zostały wykonane prawidłowo. Pozostaje weryfikacja praktyczna.
Pomiary kostki
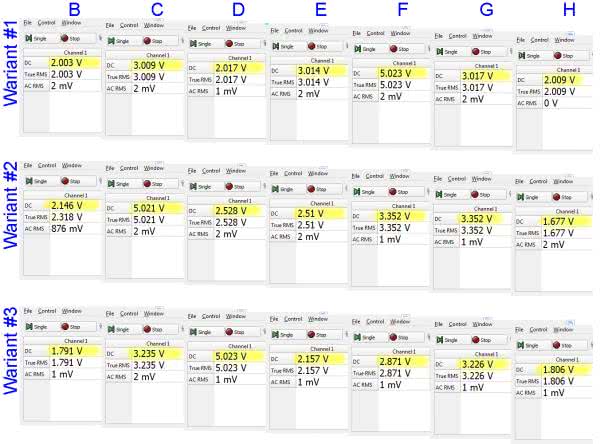
Do pomiarów w zasadzie wystarczyłby zwykły woltomierz, ponieważ jednak zawsze w części praktycznej używaliśmy zestawu Analog Discovery 2, również i teraz z niego skorzystamy. Pomiar wykonujemy za pomocą narzędzia Voltmeter, używając 1. kanału. Kostkę zasilamy zasilaczem zestawu, ustawiając w nim napięcie 5 V. Mierzymy tylko napięcia węzłowe, masa miernika i masa zasilacza są wewnętrznie połączone w przyrządzie. Do kostki wystarczy więc dopiąć się jednym kabelkiem masowym. Dla wygody końcówki kabelków mogą być dołączone do krokodylków, którymi łatwo będzie przepinać się między kolejnymi punktami pomiarowymi. Wyniki wszystkich pomiarów pokazano na rysunku 15.
Z dokładnością do błędów pomiarowych zgadzają się one z obliczeniami i symulacją.
Jarosław Doliński, EP

 Zaloguj
Zaloguj