Technika cyfrowa zdominowała współczesną elektronikę, jest więc powszechnie stosowana również w aparaturze pomiarowej, do której zaliczmy m.in. generatory. Niezwykle popularne od lat 80. XX w. generatory funkcyjne działały na zasadzie podobnej do tej, którą prezentowaliśmy ostatnio.
Jako pierwotny, budowaliśmy generator przebiegu piłokształtnego. Jest to zadanie stosunkowo proste. Idea opiera się na ładowaniu i rozładowywaniu kondensatora prądem stałym, a budowa źródła prądowego nie sprawia większego problemu technicznego. Mając przebieg piłokształtny, łatwo przerobić go na przebieg prostokątny, dodając równie prosty w wykonaniu przerzutnik Schmitta, a za pomocą diodowego układu kształtującego ostatecznie można otrzymać sinusoidę. Uzyskiwana tą nieskomplikowaną metodą zawartość harmonicznych na poziomie 1,2 procent należy uznać za dobrą.
Tym razem do wygenerowania sinusoidy zastosujemy wyłącznie technikę cyfrową. Oznacza to, że kształt przebiegu, który notabene może być dowolny, nie tylko sinusoidalny, będzie odtworzony z cyfrowej postaci zapisanej w jakiś sposób w układzie elektronicznym. Eksperyment, który teraz zrobimy nie jest jednak czystą techniką DDS.
Obliczenia
Jak zwykle zaczynamy od obliczeń w Excelu. Wygenerujemy w nim przebieg sinusoidalny, a następnie utworzymy wg pewnego algorytmu jego postać cyfrową. Aby arkusz miał cechy uniwersalności, parametry przebiegu ustalimy parametrycznie. Będą to:
- częstotliwość sygnału fs – komórka $R$1, przyjmujemy fs=1 kHz,
- częstotliwość kroku obliczeniowego fp – $R$2, przyjmujemy 100 kHz,
- okres kroku obliczeniowego Tp – R3 (R3=1/$R$2), Tp=0,00001 s,
- amplituda sygnału Um – R4 (przyjmujemy, że jest ona równa 0,95 umownych jednostek),
- liczba poziomów lp – R5 (parametr ten określa liczbę poziomów cyfrowej postaci przebiegu), przyjmujemy lp=8,
- skok napięcia dla jednego poziomu du – R6 (R6=1/$R$5), du=0,125.
W kolumnie A umieszczamy kolejne wartości czasu które narastają od zera do pełnego okresu przebiegu, czyli w naszym przypadku do 1 ms. Krok przyrostu czasu jest równy Tp.
Kolumna B zawiera definicję przebiegu. Przykładowa formuła wpisana do komórki B1 jest następująca:
=$R$4*SIN(2*PI()*$R$1*$A1)+1
Jedynka dopisana na końcu jest potrzebna, gdyż nasz układ fizyczny, który zbudujemy później, będzie generował tylko napięcia dodatnie.
Kolejnym krokiem obliczeń jest ucyfrowienie przebiegu. Jest to operacja, którą w układach rzeczywistych nazywa się kwantyzacją. Kwantyzacja zostanie zrealizowana przez formułę zapisaną w kolumnie C. Przykładowa formuła z komórki C1 jest następująca:
=LICZBA.CAŁK(B1/(2/$R$5))
Wartość chwilową przebiegu dzielimy przez dwa dzielone przez liczbę poziomów i z całości jest obliczana liczba całkowita. Liczba 2 określa maksymalny zakres przetwarzania (od 0 do 2). W tym przedziale musi zmieścić się cały przebieg. Ponieważ matematyczna sinusoida ma amplitudę 1, to aby zmieściły się obie połówki przebiegu – dodatnia i ujemna, przyjęliśmy całkowity zakres przetwarzania równy 2 i zastosowaliśmy przesunięcie sinusoidy o 1. Ponadto, pozostawiliśmy pewien margines między szczytem sinusoidy a zakresem przetwarzania ustalając amplitudę generowanego przebiegu równą 0,95. Formułę z komórki C1 powielamy w dół do końca danych.
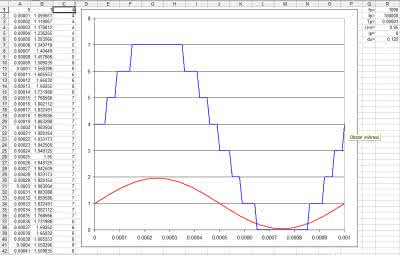
Dla sprawdzenia poprawności obliczeń możemy sporządzić wykresy przebiegu teoretycznego (czerwony wykres na rysunku 1) i wygenerowanego cyfrowo (wykres niebieski). Wygląda na to, że obliczenia są prawidłowe. Przyjęliśmy 8 poziomów i jak widać na rysunku są one kodowane liczbami od 0 do 7.
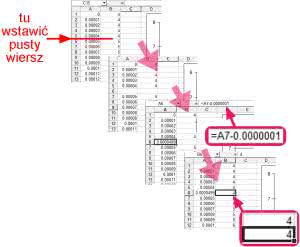
Jest jeszcze tylko pewien szczegół, który różni tak uzyskany przebieg od tego, który zostanie wygenerowany w układzie fizycznym. Chodzi o szybkość przeskoków z jednego stanu do drugiego. W układzie fizycznym czas przełączenia jest uzależniony od czasu propagacji zastosowanego elementu cyfrowego i wynosi kilka, kilkanaście nanosekund. To niestety jest zła wiadomość, gdyż tak nagłe zmiany przebiegu będą generowały sporo harmonicznych, które niekorzystnie wpłyną na parametry cyfrowej sinusoidy. Warto to sprawdzić w symulacji, ale konieczne jest utworzenie przebiegu zbliżonego do rzeczywistego. W tym celu, aby nie utracić danych kopiujemy arkusz, na którym pracujemy do tej pory i w nowym arkuszu zaznaczamy całą kolumnę C, którą następnie kopiujemy i wklejamy „specjalnie” na kolumnę B z opcją „tylko wartości”. Dane z całej kolumny C można już usunąć. Teraz nad wierszem, w którym występuje zmiana wartości w kolumnie B należy wstawić pusty wiersz i wstawić w nim w kolumnie A wartość z kolumny A z następnego wiersza pomniejszoną np. o 0,0000001. W kolumnie B natomiast wstawiamy wartość z kolumny B wiersza poprzedzającego. Przykład działań przedstawiono na rysunku 2. Czynność te powtarzamy dla każdej zmiany wartości w kolumnie B.
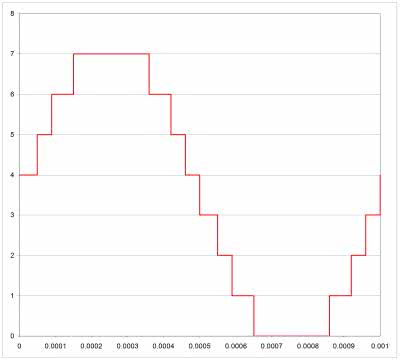
W efekcie uzyskujemy prawidłowy cyfrowy przebieg, z jakim będziemy mieć do czynienia w układzie fizycznym (rysunek 3).
To już właściwie wszystko. Uzyskaliśmy cyfrową postać sinusoidy. W oryginalnym, surowym kształcie, przy założonej liczbie poziomów, sinusoida wygląda dość kiepsko, ale założenie było bardzo słabe. 8 poziomów odpowiada rozdzielczości 3 bitów. Założenie takie było przyjęte z premedytacją, aby sprawdzić czy tak proste rozwiązanie może sprawdzić się w przypadkach, gdy nie jest wymagana super duża czystość przebiegu. W jednym z poprzednich odcinków był przytaczany przykład turystycznych przetwornic napięciowych, w których przebieg sinusoidalny imitujący napięcie sieci 230 V jest zastępowany przebiegiem trapezoidalnym. W tym eksperymencie przebieg bardziej przypomina sinusoidę, a przecież musi on zostać poddany filtracji, tak jak każdy przebieg tworzony cyfrowo. O tym jaki będzie tego skutek przekonamy się już w symulacji i pomiarach.
Przygotowanie do symulacji
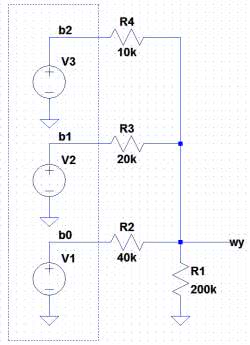
Dalej właściwie nie wiemy, jak obliczona sinusoida ma być generowana w układzie. Na razie wiemy tylko, w których momentach czasowych występują zmiany poziomów. Poszczególne poziomy muszą być tworzone w jakimś przetworniku cyfrowo-analogowym. Będzie nim rezystorowa drabinka wagowa. Jej konstrukcję pokazano na rysunku 4.
Źródła V1...V3 reprezentują wyjścia układu cyfrowego. Generowane przez nie przebiegi utworzymy za chwilę. Każde wyjście ma swoją binarną wagę. Źródło V1 ma wagę 1. Jeśli jest ono aktywne (jako jedyne), na wyjściu występuje napięcie u; analogicznie, jeśli jest aktywne tylko źródło V2 (waga 2), na wyjściu wystąpi napięcie 2u, dla źródła V3 (waga 4), będzie to 4u. Napięcia są sumowane na rezystorze R1. Jeśli w danym momencie aktywnych jest kilka źródeł, na wyjściu występuje ich sumowanie. Na przykład aktywne są źródła V1 i V3, na wyjściu wystąpi napięcie o umownej wartości u+4u=5u. W rzeczywistości, jeśli użyjemy układów cyfrowych działających w logice 3,3 V, w powyższym przykładzie na wyjściu wystąpi napięcie 458,333 mV (jest to napięcie u), co wynika z zasady superpozycji. Obliczenia pozostawiam do samodzielnego wykonania. Dla aktywnych wyjść V1 i V3 na wyjściu wystąpi napięcie u+4u=2,2917 V.
Wracamy do definiowania napięć poszczególnych źródeł. Musimy ponownie sięgnąć do Excela. Napięcia wyjściowe są zakodowane w kolumnie B w zapisie dziesiętnym (rysunek 5). Musimy je przekodować na wartości binarne i rozpisać każdą cyfrę zapisu binarnego w oddzielnej kolumnie.
W tym celu w wierszu 1 w kolumnach od D do F zapisujemy przedstawione niżej formuły, które kopiujemy w dół do końca danych:
D1: =ZAOKR.DO.CAŁK($B1/4)
E1: =ZAOKR.DO.CAŁK(($B1-4*$D1)/2)
F1: =ZAOKR.DO.CAŁK($B1-4*$D1-2*$E1)
Dane z tych kolumn w połączeniu z kolumną A, w której jest zapisany czas, stanowią definicje źródeł V1...V3 użytych w symulatorze LTspice. We właściwościach tych źródeł wybieramy opcję PWL FILE. Konieczne jest zatem utworzenie trzech plików tekstowych zawierających czas i odpowiadające mu napięcie. Zakładamy zastosowanie układów działających w logice 3,3 V, więc wszystkie jedynki w omówionym wyżej arkuszu muszą być zastąpione wartością 3,3. Można to zrobić najlepiej na kolejnej kopii arkusza. Najpierw zaznaczmy całe kolumny D,E i F, a następnie kopiujemy je „specjalnie” w wolne miejsce z opcją „tylko wartości”. Następnie, w kolejnej wolnej kolumnie wpisujemy wartości 3,3, kolumnę tę w całości kopiujemy do pamięci podręcznej (Ctrl-C), zaznaczamy kolumny utworzone w poprzednim kroku i wybieramy komendę „Wklej specjalnie” z opcją „przemnóż”. W efekcie powinniśmy uzyskać arkusz, którego fragment pokazano na rysunku 6. W tym momencie kolumny B...G nie są już potrzebne, można je wykasować.
Ostatni etap przygotowań, to utworzenie plików tekstowych zawierających definicje źródeł symulatora. Można to robić tak. Kopiujemy wszystkie dane z kolumn A i B do pamięci podręcznej i wklejamy je do notatnika, a z niego zapisujemy w postaci tekstowej np. do pliku bit2.txt umieszczanego w tym samym folderze, w którym będzie zapisywana symulacja LTspice. Usuwamy kolumnę B. Teraz jej pozycję zajęły dane dla drugiego źródła. Postępujemy podobnie: kopiujemy kolumny A i B do clipboardu, wklejamy do czystego notatnika i zapisujemy w pliku bit1.txt.
Została do wykonania analogiczna operacja dla ostatniego źródła, które będzie zdefiniowane danymi z pliku bit0.txt. Ufff. Koniec. Przechodzimy do symulacji.
Symulacja
Schemat ideowy układu symulowanego pokazano na rysunku 7. Trzy źródła napięciowe działają w trybie PWL FILE odtwarzając przebiegi zapisane w plikach bit0.txt, bit1.txt i bit2.txt. Wygenerowane z arkusza excelowego dane są nadmiarowe, ponieważ występują w nich wielokrotnie następujące po sobie chwile czasowe, w których napięcie nie ulega zmianie.
LTspice wymaga jedynie podawania tych chwil, w których zmienia się napięcie źródła. Nie stanowi to jednak problemu dla symulacji, ponieważ program wykrywa takie przypadki i automatycznie usuwa z danych wejściowych branych do obliczeń. Dane z plików tekstowych obejmują tylko jeden okres przebiegu, aby zapewnić ich ciągłość, konieczne jest dopisanie opcji repeat – endrepeat. Trzeba to zrobić ręcznie edytując opis parametrów każdego źródła. Poprawione formuły wyglądają następująco:
źródło V1: PWL repeat forever(file=bit0.txt)endrepeat
źródło V2: PWL repeat forever(file=bit1.txt)endrepeat
źródło V3: PWL repeat forever(file=bit2.txt)endrepeat
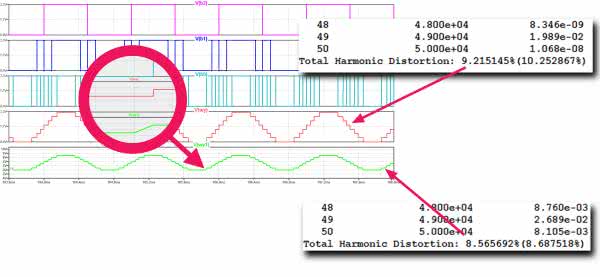
Przeprowadzimy symulację czasową tak, aby można było przyjrzeć się przebiegom z każdego źródła i oczywiście zobaczyć czy na wyjściu uzyskamy przebieg taki samu jak to obliczył Excel. Najpierw zajmiemy się surową sinusoidą, bez żadnej filtracji wyjściowej. Oszacujemy współczynnik zawartości harmonicznych. Częstotliwość generowanej sinusoidy jest równa 1 kHz, ale ponieważ w przebiegu występują skoki napięcia, można spodziewać się dużej liczby harmonicznych. W obliczeniach THD uwzględnimy ich 50. Polecenie obliczania harmonicznych i współczynnika THD jest następujące:
.four 1k 50 v(wy) v(wy1)
Przy okazji porównamy zniekształcenia naszego układu z sinusoidą generowaną w układzie bez wyostrzonych przejść między stanami (tak jak na rysunku 1). Taki przebieg występuje na wyjściu „wy1”.
Po uruchomieniu symulacji poleceniem .tran 0 200m 2m. W pustym oknie wykresu wprowadzamy 5 paneli (prawy przycisk myszki → ”Add Plot Pane” i tak 5 razy). Następnie klikamy lewym przyciskiem na pierwszy panel od góry i wskazujemy węzeł b2 klikając na niego lewym przyciskiem.
Powtarzamy tę czynność dla każdego źródła, umieszczając jego przebieg w kolejnych panelach. W czwartym od góry panelu umieszczamy przebieg wyjściowy (z węzła „wy”), a w ostatnim przebieg z węzła „wy1”. Ponieważ czas symulacji jest wielokrotnie dłuższy od okresu przebiegu, konieczne będzie rozciągnięcie wykresu. Robimy to obrysowując wąski jego wycinek trzymając naciśnięty lewy przycisk myszki i na końcu zwalniając go.
Na ekranie powinien ukazać się powiększony fragment przebiegów, na przykład taki jak na rysunku 8.
Jak widać, surowa sinusoida słabo przypomina prawdziwą sinusoidę. Przebieg jest bardziej podobny do trapezu niż do sinusoidy. Pomiar zniekształceń harmonicznych THD też potwierdza słabą jakość przebiegu. Sinusoida uzyskana z drabinki ma THD=9,22%, a dla teoretycznego przebiegu z Excela współczynnik THD jest równy 8,57% – niewiele lepiej. Tylko... tak się nie robi.
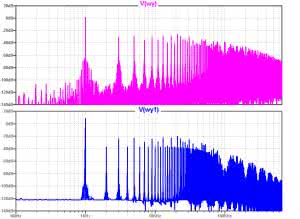
Utworzony cyfrowo sygnał zawsze będzie charakteryzował się dużą zawartością produktów obróbki cyfrowej. Widmo obu sygnałów pokazano na rysunku 9.
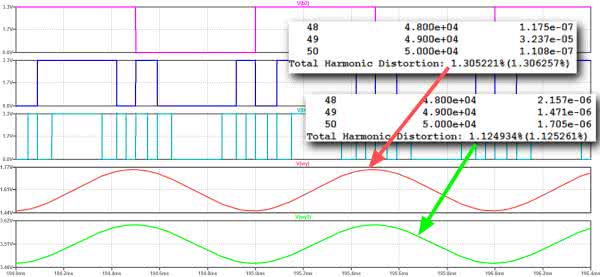
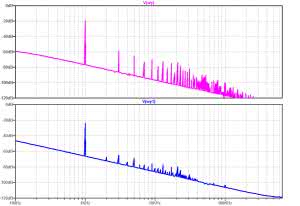
Teraz już wiadomo, dlaczego do obliczenia zawartości harmonicznych pod uwagę wzięto ich aż 50. Zobaczmy, jak na jakość sygnału wpłynie choćby najprostsze filtrowanie? Dołączamy do wyjścia kondensator 330 nF, w układzie referencyjnym zastosujemy filtr RC z elementami R=20 kΩ i C=330 nF. Wyniki czasowe pokazano na rysunku 10, a na rysunku 11 widmo. Konsekwencją takiego działania jest jednak zmniejszenie amplitudy sygnału wyjściowego. Harmoniczne na poziomie 1,3% są już do przyjęcia. Pora na weryfikację praktyczną.
Pomiary
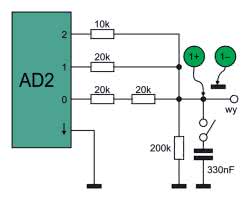
Najpierw musimy zbudować jakiś układ cyfrowy, który będzie generował sekwencję cyfrową obliczoną w Excelu. Zastosujemy do tego generator przebiegów wzorcowych – narzędzie Patterns zestawu Analog Discovery 2, do którego dołączymy zewnętrzne rezystory tworzące drabinkę wagową.
Schemat połączeń pokazano na rysunku 12. Pojawia się jednak problem, jak wpisać sekwencję cyfrową do generatora? Można to oczywiście zrobić ręcznie, tak bardzo dużo danych nie ma, żeby nie było to możliwe. My jednak zastosujemy metodę bardziej uniwersalną.
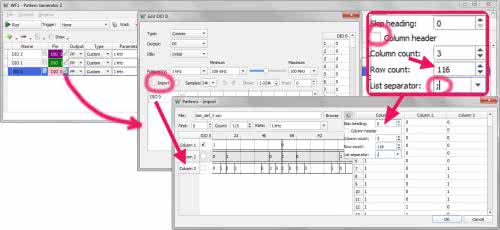
W tym celu musimy jeszcze raz wrócić do Ecela. Komórki z obliczonymi zerami i jedynkami skopiować jako wartości (bez formuł) do nowego arkusza, a następnie zapisać ten arkusz w formacie CSV (np. w pliku sin_def_V.csv w folderze roboczym LTspice’a). Teraz można już otworzyć narzędzie Patterns i dodać w nim 3 nowe kanały (kliknąć na przycisk „Click to Add channels). Kanały muszą być typu „Signal”. Z listy wybieramy kanały DIO0, DIO1 i DIO2. Każdy kanał musi być typu „Custom”. Trzeba to zmienić, jeśli domyślny typ będzie inny. Kolejnym krokiem konfiguracji jest ustalenie rodzaju wyjścia – w każdym kanale w kolumnie „Output” wybieramy pozycję „PP” (push-pull). Pozostała najważniejsza operacja, czyli wpisanie odpowiednich sekwencji w odpowiednie miejsca. Robimy to kolejno dla każdego kanału. W tym celu należy kliknąć na przycisk z długopisem znajdujący się z prawej strony nazwy kanału (rysunek 13), nacisną przycisk „Import”, wskazać folder i odpowiedni plik CSV.
Do kanału 0 wpisujemy dane z kolumny 3. Analogicznie: kanał 1 – kolumna 2, kanał 2 – kolumna 1. Ważne jest, aby wyłączyć opcję nagłówka kolumny i ustawić jako separator znak średnika. Jest to możliwe po naciśnięciu trybika znajdującego się obok przycisku „Browse”. Pełny cykl naszej sinusoidy składa się ze 116 taktów, więc ustawienie częstotliwości 116 kHz w kolumnie „Parameter1” każdego kanału spowoduje wygenerowanie sinusoidy o częstotliwości 1 kHz. Wszystko gotowe.
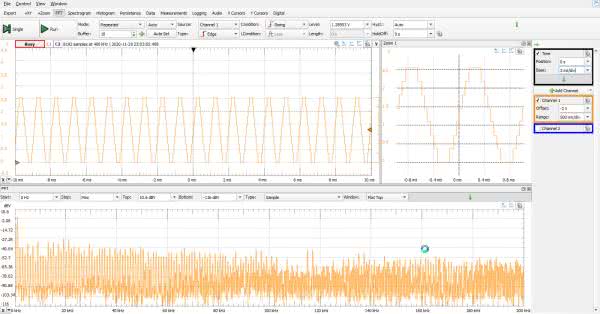
Uruchamiamy generator (rysunek 14) i oscyloskop, którego 1. kanał dołączamy do wyjścia drabinki. Najpierw bez kondensatora (rysunek 15).
W oknie oscyloskopu włączamy funkcję „Zoom” i „FFT”. Okazuje się, że uzyskana na razie pseudosinusoida dokładnie odpowiada tej z obliczeń i symulacji. Widmo również wykazuje bardzo dużą zawartość harmonicznych. Pomiar współczynnika THD zmierzony narzędziem Spectrum Analyzer dał wynik –20,41 dBc, czyli 9,54%. Niemal dokładnie zgadza się to z symulacją.
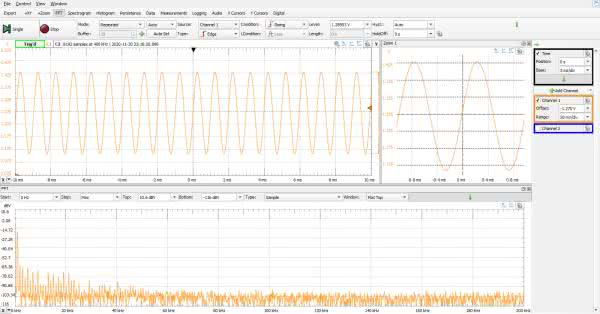
Wykonaliśmy pomiar w pośredniej fazie realizacji projektu. Wiemy, że taki generator bez kondensatora wyjściowego nie ma prawa działać prawidłowo. Dołączamy więc do wyjścia kondensator 330 nF i ponawiamy pomiary.
Teraz sinusoida przypomina już bardziej matematyczny ideał (rysunek 16), ale trzeba sprawdzić jak bardzo do ideału zbliżyliśmy się. Pomiar THD tym razem dał wynik –38,82 dBc, czyli 1,15%. Jest to znowu niemal dokładne powtórzenie wyniku z symulacji, a z technicznego punktu widzenia wynik 1,15% choć nie jest rewelacyjny, to w wielu amatorskich pomiarach akceptowalny. Jeśli weźmiemy pod uwagę, że taki rezultat został osiągnięty przy zastosowaniu 3-bitowego przetwarzania, to na pewno należy go uznać jako bardzo dobry.
Nie omówiliśmy jeszcze wszystkich zagadnień związanych z generowaniem przebiegów elektrycznych, ale żeby nie męczyć za bardzo materiału na razie temat kończymy.
Jarosław Doliński, EP

 Zaloguj
Zaloguj