Detekcja częstotliwości z wykorzystaniem algorytmu Goertzel’a

Niedziela, 26 Styczeń 2020

Tagi:

Mikrokontrolery

Detekcja częstotliwości z wykorzystaniem algorytmu Goertzel’a

W praktyce elektronika programisty zdarzają się takie projekty, gdzie zachodzi potrzeba detekcji obecności pewnej częstotliwości wzorcowej w złożonym sygnale. Oczywiście zagadnienie takie można zrealizować sprzętowo stosując odpowiednie filtry jednak, skoro już mamy „na pokładzie” mikrokontroler to można zadanie to zrzucić na „barki” oprogramowania.

Oczywistym rozwiązaniem, które przychodzi do głowy jest zastosowanie szybkiej transformaty Fourier’a (FFT) w celu realizacji wspomnianej wyżej funkcjonalności, lecz technika ta nie jest pozbawiona wad, które nie rzadko dyskwalifikują jej zastosowanie w systemach o ograniczonej mocy obliczeniowej. Wynika to z faktu, iż typowa implementacja szybkiej transformaty Fourier’a wymaga przeprowadzenia sporej liczby dokładnych obliczeń na liczbach rzeczywistych, w tym implementacji funkcji trygonometrycznych. O ile dla mikrokontrolerów 32-bitowych wyposażonych w jednostki zmiennoprzecinkowe nie będzie to stanowiło bariery o tyle w systemach 8-bitowych o ograniczonej mocy obliczeniowej będzie to nie lada wyzwanie, którego praktyczna realizacja jest mocno ograniczona.

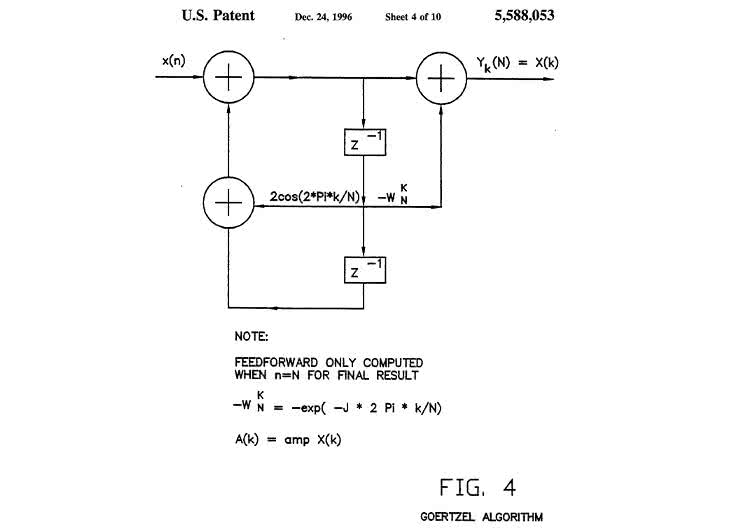
W niektórych zastosowaniach implementacja szybkiej transformaty Fourier’a jest nadmiarowa i nieefektywna. Dotyczy to tych systemów, gdzie nie ma potrzeby analizy całego widma sygnału, lecz konkretnej, poszukiwanej częstotliwości. I właśnie wtedy z pomocą przychodzi nam algorytm Goertzel’a, który pozwala na obliczenie amplitudy i mocy sygnału o szukanej częstotliwości w paśmie badanego sygnału. W wielu zastosowaniach jest to w zupełności wystarczające a angażuje znacznie mniejsze moce obliczeniowe. Takim, „flagowym” zastosowaniem wspomnianej techniki jest detekcja tonów DTMF w sygnale fonicznym telefonii, jednak algorytm ten sprawdzi się w każdym przypadku, gdzie w złożonym sygnale poszukujemy obecności pewnej, określonej częstotliwości.

Przejdźmy do konkretów. Nie będę przytaczał całej teorii towarzyszącej temu ciekawemu zagadnieniu, skupię się na realizacji programowej, głównie dlatego, że zagadnienie od strony teoretycznej jest dość obszerne, zaś od strony praktycznej, niezmiernie proste.

Dociekliwi Czytelnicy znajdą bez problemu podstawy teoretyczne w czeluściach Internetu (choćby na Wikipedii).

Podstawowe założenia

Pierwszym zadaniem z jakim musimy się zmierzyć w procesie detekcji szukanej częstotliwości jest wybór częstotliwości próbkowania sygnału. W tym przypadku rozwiązanie jest dość oczywiste i wynika z prawa Nyquist’a. Częstotliwość próbkowania fs musi być równa co najmniej podwójnej częstotliwości poszukiwanego sygnału ft. Dla przykładu, jeśli w badanym sygnale poszukujemy częstotliwości 440 Hz to częstotliwość próbkowania powinna wynosić co najmniej 880 Hz.

Kolejnym krokiem jest określenie niezbędnej liczby próbek N. Generalnie i w dużym uproszczeniu, czym więcej tym lepiej, ale trzeba mieć na uwadze kilka istotnych zależności:

liczba próbek N jest tutaj ekwiwalentem liczby punktów szybkiej transformaty Fourier’a a zatem determinuje rozdzielczość algorytmu a co za tym idzie jego dokładność. Dla przykładu, jeśli częstotliwość próbkowania sygnału fs wynosi 880 Hz, zaś N równe jest 100 to wynikowa rozdzielczość wynosi 880 Hz/100=8,8 Hz,
czym większa liczba próbek N tym dłużej będziemy czekać na detekcję szukanego sygnału, gdyż więcej czasu upłynie zanim zbierzemy wszystkie jego próbki,
trzecim czynnikiem warunkującym wybór liczby próbek N jest zależność pomiędzy częstotliwością poszukiwanego sygnału ft a wspomnianą wcześniej rozdzielczością (fs/N). Innymi słowy częstotliwość poszukiwanego sygnału ft powinna być wielokrotnością otrzymanej rozdzielczości sygnału (fs/N).

Implementacja programowa

Pierwszą rzeczą, którą musimy wykonać to obliczenie 4 współczynników wejściowych na podstawie wybranych parametrów ft, fs i N. Wartości tych współczynników należy wyznaczyć na podstawie obliczeń i zapisać, jako stałe w programie obsługi, co pozwoli na ograniczenie rozmiaru kodu wynikowego. Wzory niezbędne do obliczenia wspomnianych wielkości pokazano poniżej:

ω = 2*π*ft/fs
sine = sin(ω)
cosine = cos(ω)
COEFF = 2*cos(ω)

Teraz potrzebne będą 3 zmienne typu float. Nazwijmy je Q0, Q1 i Q2. Zmienna Q1 reprezentuje wartość Q0 podczas poprzednich obliczeń, zaś Q2 reprezentuje wartość Q0 dwie iteracje wcześniej lub innymi słowy wartość Q1 podczas poprzednich obliczeń. Co ważne, zmienne Q1 i Q2 muszą być zerowane na początku każdego bloku obliczeń (N). Wszystko, co musimy teraz zrobić to wykonać obliczenia, jak niżej dla każdej, pozyskanej próbki danych Sample:

Q0 = COEFF * Q1 - Q2 + Sample;
Q2 = Q1;
Q1 = Q0;

Wykonanie tych obliczeń możemy powierzyć, dla przykładu, funkcji obsługi przerwania przetwornika ADC zbierającego dane lub wykonać je N-razy w pętli głównej po zebraniu wszystkich N-próbek sygnału. Dalej, po wykonaniu N-iteracji obliczeń, jak wyżej, wyznaczamy wartości rzeczywiste, urojone oraz moc sygnału według algorytmu Goertzel’a według poniższych wzorów:

Real = (Q1 – Q2 * Cosine)
Imag = (Q2 * Sine)
Power = Real2 + Imag2

Jeśli nie zależy nam na poznaniu fazy sygnału, a co za tym idzie wartości rzeczywistej i urojonej, a wyłącznie na obliczeniu mocy sygnału (co wystarczy do potwierdzenia jego obecności), możemy skorzystać z uproszczonego wzoru na jej wyznaczenie, który wygląda następująco:

Power = Q12 + Q22 - Q1 * Q2 * COEFF

W przypadku uproszczonego wzoru potrzebny będzie wyłącznie jeden współczynnik obliczeniowy a mianowicie COEFF. Mając z kolei obliczoną moc sygnału według algorytmu Goertzel’a możemy, stosując dobraną eksperymentalnie wartość progową (tzw. threshold), określić czy przebieg o szukanej częstotliwości ft znajduje się w badanym sygnale czy też nie. To tyle! Prawda, że proste? Na listingu 1 pokazano funkcję obliczającą moc sygnału według algorytmu Goertzel’a.

Listing 1. Funkcja obliczającą moc sygnału według algorytmu Goertzel’a

float Goertzel(void) {
	float Q0, Q1 = 0, Q2 = 0, Power;

	//Dla każdej próbki sygnału wykonujemy poniższe obliczenia
	for (uint16_t Idx = 0; Idx < N; ++Idx) {
		Q0 = COEFF * Q1 - Q2 + Sample[Idx];
		Q2 = Q1;
		Q1 = Q0;
	}

	//Na koniec obliczamy zoptymalizowaną wartość algorytmu Goertzel-a
	Power = sqrt(Q1*Q1 + Q2*Q2 - COEFF*Q1*Q2);

	return Power;
}

W zaprezentowanej na listingu 1 funkcji użyto dwóch stałych:

N określającą liczbę próbek sygnału,
COEFF określającą obliczony wcześniej współczynnik algorytmu Goertzel’a (w tym wypadku 0,618).

W praktyce

Załóżmy, że w badanym sygnale poszukujemy przebiegu o częstotliwości ft=200 Hz. Przyjmijmy zatem, z pewnym zapasem, że częstotliwość próbkowania równa jest fs=1000 Hz, zaś liczba próbek sygnału równa 50. Z powyższych założeń otrzymujemy rozdzielczość algorytmu równą fs/N=20 Hz a zatem poszukiwana częstotliwość ft (200 Hz) będzie wielokrotnością rozdzielczości.

Obliczamy niezbędne współczynniki:

ω = 2*π*200/1000 = 1,2566,

a zatem

COEFF = 2*cos(ω) = 0,618

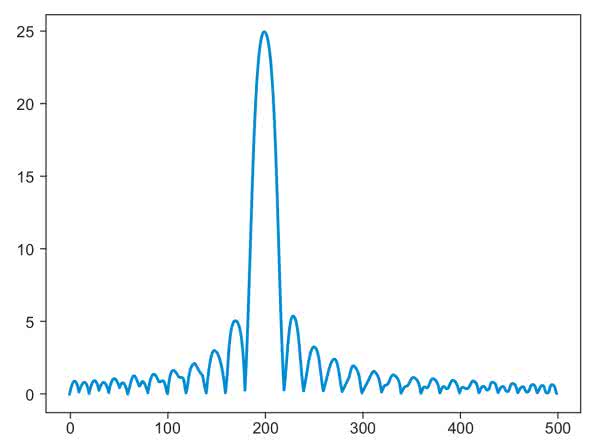
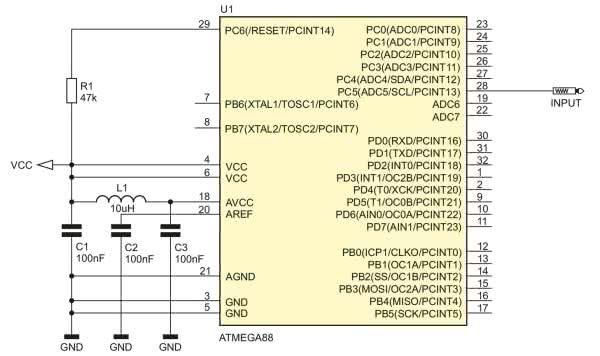
Rysunek 1. Zależność mocy sygnału od częstotliwości dla współczynnika ω=0,618 (symulacja)

Obliczone wartosci podstawiamy do funkcji algorytmu Goertzel’a i wykonujemy symulację, której wynik pokazano na rysunku rysunku 1. Widzimy zdecydowane maksimum dla założonej częstotliwości równej 200 Hz. Pomiary praktyczne zrealizujemy na bazie prostego systemu pomiarowego z mikrokontrolerem ATmega88, któego schemat pokazano na rysunku 2.

Rysunek 2. Schemat prostego systemu pomiarowego z wykorzystaniem mikrokontrolera ATmega88

Pomiary testowe wykonamy z użyciem generatora przebiegu sinusoidalnego, który dostarcza przebieg o częstotliwościach w zakresie 0…500 Hz oraz prostego systemu akwizycji danych zbudowanego z użyciem przetwornika ADC wbudowanego w strukturę mikrokontrolera ATmega88 pracującego z rozdzielczością 8 bitów. Funkcję konfigurująca przetwornik ADC do wykonywania pomiarów jak wyżej pokazano na listingu 2, zaś na listingu 3 pokazano ciało funkcji odpowiedzialnej za wykonanie pomiaru.

Listing 2. Funkcja konfigurująca przetwornik ADC do wykonywania pomiarów

void ADCinit(void) {
	//Uruchomienie i konfiguracja przetwornika ADC: Vref=1.1V, Vin=ADC5
	ADMUX = (1<<REFS1)|(1<<REFS0)|(1<<ADLAR)|(1<<MUX2)|(1<<MUX0);
	//Uruchomienie przetwornika ADC i start pierwszej konwersji 
	//by kolejne trwały krócej, preskaler=64 (125kHz @ 8MHz)
	ADCSRA = (1<<ADEN)|(1<<ADSC)|(1<<ADPS2)|(1<<ADPS1);
}

Listing 3. Funkcja odpowiedzialna za wykonanie pomiaru ADC

inline uint8_t ADCread(void) {
	//Uruchomienie przetwornika ADC i start konwersji, 
	//preskaler=64 (125kHz @ 8MHz)
	ADCSRA = (1<<ADEN)|(1<<ADSC)|(1<<ADPS2)|(1<<ADPS1);
	//Czekamy na zakończenie bieżącej konwersji - 116us
	while(ADCSRA & (1<<ADSC));

	return ADCH;
}

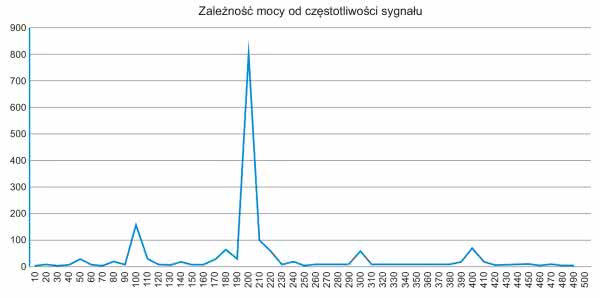
Pomiary napięcia inicjowane są przerwaniem z układu czasowo-licznikowego TIMER1, który dokładnie co 10 ms (100 razy na sekundę) inicjuje pomiar ADC. Wynikiem działania naszego algorytmu jest liczba typu float, której wartość zależy od częstotliwości badanego sygnału. Na rysunku 3 pokazano pozyskany praktycznie wykres zależności wartości algorytmu Goertzel’a (mocy sygnału) w funkcji częstotliwości dla założonych wcześniej parametrów wyjściowych determinujących wartość współczynnika COEFF.

Rysunek 3. Wykres zależności wartości algorytmu Goertzel’a (mocy sygnału) w funkcji częstotliwości

Otrzymany przebieg pokrywa się z wynikami symulacji, gdyż dla częstotliwości równej 200 Hz występuje zdecydowane maksimum funkcji Goertzel’a co potwierdza wcześniejsze założenia teoretyczne. Jak mogliśmy się przekonać jest to dość proste zagadnienie programistyczne, dlatego zachęcam zainteresowanych Czytelników do testów praktycznych.

Robert Wołgajew, EP