Teraz połączmy kolejne „motylki” w pełne FFT. Jak pokazuje rysunek 18, jest to bardzo proste. Łączymy tu wejścia kolejnego modułu z wyjściami poprzedniego. Po kolei umieszczamy „motylki” rzędu N, N/2, aż do 2. Łącznie będzie ich log2N. W naszym projekcie liczba bitów przypadających na wejście i wyjście jest taka sama. Dzięki temu nie musimy się martwić szerokością wektorów pomiędzy kolejnymi etapami obliczeń. Ponieważ w każdym kroku realizujemy dodatkowe dzielenie przez 2, końcowy wynik będzie podzielony przez 2log2N, czyli N.
Na końcu widzimy jeszcze dodatkowy moduł licznika modulo N. Zlicza on, gdy na wyjściu FFT pojawi się poprawna dana. Jego wyjście q przechodzi przez blok odwracający kolejność bitów. W ten sposób powstaje trzecie wyjście naszego modułu, czyli adres próbki. Wejścia reset wszystkich modułów butterfly oraz licznika łączymy razem.
Implementacja FFT została pokazana na listingu 7. Przyjmuje on dwa, dobrze już nam znane parametry. N jest liczbą próbek, a K liczbą bitów przypadających na jedną liczbę. Następnie znajdziemy listę wejść i wyjść. Są one identyczne jak dla pojedynczego motylka, poza dodatkowym wyjściem addr, które przyjmuje wartości od 0 do N-1. Dlatego jego długość to $clog2(N).
10 module fft #(
11 parameter K = 8,
12 parameter N = 2,
13 parameter LOG_N = $clog2(N)
14 ) (
15 input wire clk,
16 input wire rst,
17 input wire signed [K-1:0]d_in_re,
18 input wire signed [K-1:0]d_in_im,
19 input wire valid_in,
20 output logic signed [K-1:0]d_out_re,
21 output logic signed [K-1:0]d_out_im,
22 output logic [LOG_N-1:0]addr,
23 output logic valid_out
24 );
25 logic signed [K-1:0]d_re[LOG_N:0];
26 logic signed [K-1:0]d_im[LOG_N:0];
27 logic valid[LOG_N:0];
28 logic [LOG_N-1:0]addr1;
29 30 assign d_re[0] = d_in_re;
31 assign d_im[0] = d_in_im;
32 assign valid[0] = valid_in;
33
34 genvar i;
35 generate
36 for (i = 0; i < LOG_N; i++) begin : BUTTERFLY
37 butterfly #(.K(K), .N(N / 2**i)) b (
38 .clk(clk),
39 .rst(rst),
40 .d_in_re(d_re[i]),
41 .d_in_im(d_im[i]),
42 .valid_in(valid[i]),
43 .d_out_re(d_re[i+1]),
44 .d_out_im(d_im[i+1]),
45 .valid_out(valid[i+1]));
46 end
47 endgenerate
48
49 counter #(.N(N)) addr_cnt (
50 .clk(clk),
51 .rst(rst),
52 .ce(valid[LOG_N]),
53 .q(addr1),
54 .ov());
55
56 assign d_out_re = d_re[LOG_N];
57 assign d_out_im = d_im[LOG_N];
58 generate
59 // assign addr = {<<{addr1}}; not supported
60 for (i = 0; i < $bits(addr); i++) begin : BIT_REV
61 assign addr[i] = addr1[$bits(addr) - i – 1];
62 end
63 endgenerate
64 assign valid_out = valid[LOG_N];
65
66 endmodule
Dalej, w liniach 25…27, znajdziemy tablicę wektorów, której użyjemy do łączenia kolejnych komponentów. Główna część znajduje się w bloku generate (34…47). Dla przypomnienia, w układzie FPGA pętla for nie oznacza wykonanie jej zawartości kilkukrotnie. Zamiast tego, każde wywołanie pętli, to umieszczenie kolejnego fragmentu sprzętu. Następnie znajdziemy instancję licznika generującego adres (linie 49…54). Aby otrzymać poprawny adres, musimy jeszcze odwrócić kolejność bitów. W języku SystemVerilog można to zrobić za pomocą instrukcji strumieniowej:
{<<{addr1}}
Niestety, nie jest ona już wspierana w programie Quartus w wersji 18. Dlatego zamiast niej użyta została kolejna pętla.
Na listingu 8 został pokazany fragment testbench-u. W wierszach 35…45 generowane są dane wejściowe. Tablica A zawiera amplitudy, natomiast a fazy kolejnych częstotliwości bazowych. Wymuszenie jest zapisane w wektorach in_re i in_im. Ponieważ generowany sygnał jest czysto rzeczywisty, druga tablica zawiera same zera.
035 initial begin
036 A[0] = 10; a[0] = 0;
037 A[1] = 40; a[1] = 0;
038 A[2] = 10; a[2] = 0;
039 A[3] = 25; a[3] = 0;
040 for (int i = 0; i < N; i++) begin
041 in_re[i] = 0; in_im[i] = 0;
042 for (int f = 0; f < N/2; f++)
043 in_re[i] += A[f] * $cos(2*pi*f*i/N+a[f]);
044 end
045 end
052 initial begin
053 valid_in = 1’b0;
054 rst = 1’b0;
055 #100ns @(negedge clk);
056 rst <= 1’b1;
057 for (int i = 0; i < 2*N; i++) begin
058 if (i < N) begin
059 d_in_re = in_re[i];
060 d_in_im = in_im[i];
061 end
062 valid_in = 1’b1;
063 @(posedge clk);
064 valid_in = 1’b0;
065 d_in_re = ‘0;
066 d_in_im = ‘0;
067 @(posedge clk);
068 end
069 valid_in = 1’b0;
070 end
071
072 fft #(.K(K), .N(N)) dut (
073 .clk(clk),
074 .rst(rst),
075 .d_in_re(d_in_re),
076 .d_in_im(d_in_im),
077 .valid_in(valid_in),
078 .d_out_re(d_out_re),
079 .d_out_im(d_out_im),
080 .addr(addr),
081 .valid_out(valid_out));
082
083 always_ff @(posedge clk) begin
084 if (valid_out) begin
085 out_re[addr] <= d_out_re;
086 out_im[addr] <= d_out_im;
087 i <= i + 1;
088 end
089 if (i == N) begin
090 rms = 0;
091 for (int i = 0; i < N; i++) begin
092 if (i == 0) begin
093 out_sim_re = A[0];
094 out_sim_im = 0;
095 end else if (i < N/2) begin
096 out_sim_re = A[i] * $cos(a[i]) / 2;
097 out_sim_im = A[i] * $sin(a[i]) / 2;
098 end else if (i == N/2) begin
099 out_sim_re = A[i] * $cos(a[i]);
100 out_sim_im = A[i] * $sin(a[i]);
101 end else begin
102 out_sim_re = A[N - i] * $cos(a[N - i]) / 2;
103 out_sim_im = A[N - i] * $sin(a[N - i]) / 2;
104 end
105 $display("s: %.2f+%.2fj h: %.2f+%.2fj",
106 out_sim_re, out_sim_im,
107 out_re[i], out_im[i]);
108 rms += (out_sim_re-out_re[i])**2 + (out_sim_im-out_im[i])**2;
109 end
110 rms = $sqrt(rms/N);
111 $display("RMS of error is %.1f", rms);
112 $stop;
113 end
114 end
Kolejna część (52…70) odpowiada za wprowadzanie danych na wejście. Dzieje się to w pętli o długości 2N (wystarczyłoby tak naprawdę półtora).
Przez pierwsze N kroków podawane są wygenerowane próbki, a później zera.
Dalej znajdziemy instancję testowanego modułu, po której następuje walidacja wyniku. Linie 84…88 odpowiadają za zapisanie danych wyjściowych w tablicy. Kiedy na wyjściu znajdzie się już wszystkie N próbek, rozpoczyna się ich porównywanie (91…109). Wartość oczekiwana i uzyskana są wypisywane w terminalu. Liczony jest także błąd średnio-kwadratowy pomiędzy nimi. Po sprawdzeniu wszystkich próbek, symulacja kończy się. Symulację możemy uruchomić, wywołując w programie ModelSim komendę:
do fft_sim.do
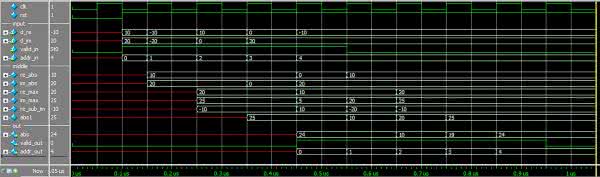
Rezultat będzie podobny do tego z rysunku 19. W pierwszych dwóch liniach widzimy sygnał zegarowy i reset. Dalej znajdują się dane wejściowe: część rzeczywista, urojona (na stałe równa 0) oraz sygnał valid. Potem znajdziemy tablicę wektorów, łączącą poszczególne motylki. Ponieważ jest ona dość duża, została zwinięta. Zachęcam Czytelnika do samodzielnego uruchomienia symulacji i przyjrzenia się jej. Na samym końcu widoczne są sygnały wyjściowe: valid, adres oraz dane. Poszczególne bloki sygnałów zostały rozdzielone separatorem i dodane w pliku 13_fft/fft_sim.do za pomocą polecenia:
add wave -divider tekst
Poza przebiegami, symulacja zwraca także porównanie wartości oczekiwanej i uzyskanej, co widać na listingu 9. Uzyskane błędy są konsekwencją kwantyzacji oraz zaokrągleń. Widzimy, że poszczególne wartości (zarówno dla części rzeczywistej jak i urojonej) nie różnią się bardziej niż ±1.
# s: 10.00+0.00j h: 9.00+0.00j
# s: 20.00+0.00j h: 19.00+-1.00j
# s: 5.00+0.00j h: 4.00+-1.00j
# s: 12.50+0.00j h: 12.00+-1.00j
# s: 0.00+0.00j h: 0.00+-1.00j
# s: 0.00+0.00j h: -1.00+-1.00j
# s: 0.00+0.00j h: -1.00+-1.00j
# s: 0.00+0.00j h: -1.00+-1.00j
# s: 0.00+0.00j h: 0.00+0.00j
# s: 0.00+0.00j h: 0.00+0.00j
# s: 0.00+0.00j h: 0.00+0.00j
# s: 0.00+0.00j h: -1.00+0.00j
# s: 0.00+0.00j h: -1.00+0.00j
# s: 0.00+0.00j h: -1.00+0.00j
# s: 0.00+0.00j h: -1.00+0.00j
# s: 0.00+0.00j h: -1.00+0.00j
# s: 0.00+0.00j h: 0.00+0.00j
# s: 0.00+0.00j h: 0.00+0.00j
# s: 0.00+0.00j h: 0.00+0.00j
# s: 0.00+0.00j h: 0.00+0.00j
# s: 0.00+0.00j h: 0.00+0.00j
# s: 0.00+0.00j h: -1.00+0.00j
# s: 0.00+0.00j h: -1.00+0.00j
# s: 0.00+0.00j h: 0.00+0.00j
# s: 0.00+0.00j h: 0.00+0.00j
# s: 0.00+0.00j h: 0.00+0.00j
# s: 0.00+0.00j h: 0.00+0.00j
# s: 0.00+0.00j h: -1.00+0.00j
# s: 0.00+0.00j h: 0.00+0.00j
# s: 12.50+0.00j h: 12.00+0.00j
# s: 5.00+0.00j h: 4.00+0.00j
# s: 20.00+0.00j h: 19.00+0.00j
# RMS of error is 0.9
Uzyskany błąd średnio-kwadratowy to 0,9.
Moduł liczby zespolonej
Dla poszczególnych częstotliwości, moduł uzyskanego wyniku odpowiada amplitudzie, a kąt – fazie. Jednak gdy będziemy badać sygnał z mikrofonu, trudno będzie uzyskać synchronizację fazy. Skupmy się więc na samej amplitudzie. Musimy obliczyć moduły kolejnych wyników.
Najprostszym rozwiązaniem byłoby skorzystanie bezpośrednio z definicji:
(23)
Jednak to podejście wymaga wykonania dwóch mnożeń, sumy oraz pierwiastkowania. Mnożenia są operacją kosztowną, lecz już wiemy jak możemy je zrealizować. Znacznie trudniejszy jest jednak pierwiastek. Można pokusić się o skorzystanie z któregoś z dostępnych algorytmów, aproksymować go wielomianem, albo stablicować, podobnie jak z funkcją sinus i cosinus. Wymyślono jednak znacznie prostsze podejście obliczania modułu. Jest to tak zwany algorytm „alfa max beta min” [2] i aproksymuje wynik za pomocą równania:
(24)
Pierwszym krokiem jest więc obliczenie modułów części rzeczywistej i urojonej. Następnie większy z nich mnożymy razy współczynnik alfa, a mniejszy razy beta. Uzyskane iloczyny sumujemy i traktujemy je jako moduł. Zmieniając wartości współczynników zmieniamy precyzję oraz trudność implementacji. Zanim jednak do niej przejdziemy, sprawdźmy jakiej dokładności możemy się spodziewać.
Jak pamiętamy dowolną liczbę zespoloną możemy przedstawić także w postaci wykładniczej:
(25)
Wtedy obliczenie jej modułu jest bardzo proste:
(26)
Podstawmy teraz postać (25) do wzoru (24):
(27)
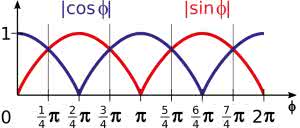
Musimy teraz ustalić dla jakich kątów który współczynnik jest większy, a który mniejszy. Wykres interesujących nas funkcji pokazuje rysunek 20.
Korzystając z niego, możemy w łatwy sposób rozbić nasz wzór na dwa przypadki:
Korzystając z niego możemy w łatwy sposób rozbić nasz wzór na dwa przypadki:
(28)
Teraz możemy już obliczyć względny błąd naszej aproksymacji:
(29)
Widzimy, że nie zależy on od amplitudy sygnału. Zmienia się jedynie z fazą. W naszej implementacji przyjmiemy współczynniki:
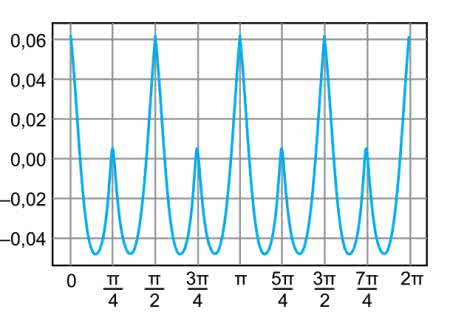
Wartość błędu w zależności od kąta pokazuje rysunek 21. Widzimy, że uzyskany wynik będzie miał błąd około ±6%. Nie jest to zły wynik, biorąc pod uwagę prostotę algorytmu.
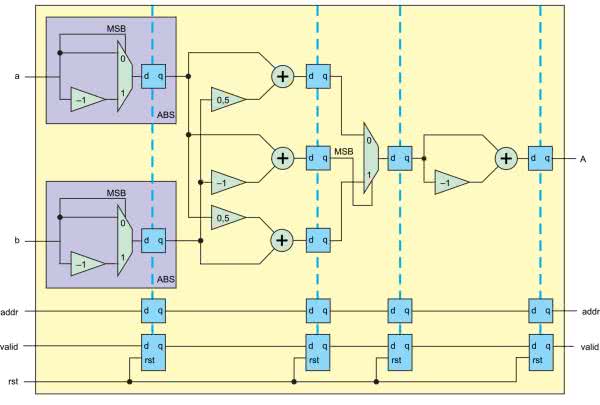
Na rysunku 22 pokazano implementację. Wejścia a i b to odpowiednio część rzeczywista i urojona, które trafiają na blok ABS, obliczający jej wartość bezwzględną. Możemy go podzielić na dwa etapy. W pierwszym realizujemy obliczenia i wyliczamy obie możliwe opcje. W tym przypadku są to: a i –a. Musimy także rozstrzygnąć, która z nich jest poprawna.
W przypadku modułu, decydujący jest znak. Można go łatwo sprawdzić, ponieważ w kodzie uzupełnienia do dwóch, decyduje o nim najstarszy bit (MSB). Kiedy jest równy 1, mamy do czynienia z liczbą ujemną, a jeśli 0 – z dodatnią. Teraz na podstawie obliczonego już warunku, multiplekser wybierze, którą wersję powinien przepuścić na wyjście. Wartości modułów są zatrzaskiwanie w rejestrach.
Aby zrozumieć kolejną część obliczeń musimy zauważyć, że możemy wyciągnąć współczynnik alfa za nawias:
(30)
Otrzymujemy dwie możliwe wartości wyrażenia w nawiasie: albo . Przy okazji oba z nich są łatwe do obliczenia: wystarczy nam przesunięcie bitowe oraz suma. Musimy jeszcze zbadać, która wartość jest większa. Zastosujemy tu bardzo proste przekształcenie:
W ten sposób sprowadziliśmy porównanie dwóch liczb, do porównania różnicy do zera. A porównanie do zera sprowadza się do sprawdzenia znaku. A to już umiemy zrobić. Możemy teraz wrócić do rysunku 22. W drugim takcie zegara zatrzaskujemy w rejestrach trzy wartości: , oraz bit znaku różnicy . W kolejnym kroku dopiero podejmujemy decyzję, który z możliwych wyników cząstkowych zostanie przepisany na wyjście.
Na sam koniec zostanie mnożenie przez . Tutaj jednak skorzystaliśmy z kolejnego „triku”:
(31)
W ten sposób otrzymujemy proste dzielenie przez potęgę 2, które sprowadzi się do przesunięcia bitów, oraz odejmowanie.
Moduł ma jeszcze trzy dodatkowe wejścia i dwa wyjścia. Są to wejście i wyjście sygnałów valid i addr. Są one opóźniane o cztery takty zegara, dzięki temu dane płyną razem z sygnałami kontrolnymi. Jak zwykle resetowany jest jedynie sygnał valid. Implementację pokazuje listing 10.
10 module abs #(
11 parameter K = 8,
12 parameter N = 2
13 ) (
14 input wire clk,
15 input wire rst,
16 input wire signed [K-1:0]d_re,
17 input wire signed [K-1:0]d_im,
18 input wire valid_in,
19 input wire [N-1:0]addr_in,
20 output logic signed [K-1:0]abs,
21 output logic [N-1:0]addr_out,
22 output logic valid_out
23 );
24 parameter LATENCY = 4;
25 logic unsigned [K-1:0]re_abs;
26 logic unsigned [K-1:0]im_abs;
27 logic unsigned [K:0]re_max;
28 logic unsigned [K:0]im_max;
29 logic signed [K:0]re_sub_im;
30 logic unsigned [K:0]abs1;
31
32 always_ff @(posedge clk) begin
33 re_abs <= d_re[K-1] ? -d_re : d_re;
34 im_abs <= d_im[K-1] ? -d_im : d_im;
35 end
36
37 always_ff @(posedge clk) begin
38 re_max <= re_abs + (im_abs >> 1);
39 im_max <= (re_abs >> 1) + im_abs;
40 re_sub_im <= re_abs – im_abs;
41 end
42
43 always_ff @(posedge clk)
44 abs1 <= re_sub_im[K] ? im_max : re_max;
45
46 always_ff @(posedge clk)
47 abs <= abs1 - (abs1 >> 4);
48
49 delay #(.N(LATENCY), .L(1)) valid (
50 .clk(clk),
51 .rst(rst),
52 .ce(1’b1),
53 .in(valid_in),
54 .out(valid_out));
55
56 delay #(.N(LATENCY), .L(N)) dut (
57 .clk(clk),
58 .rst(1’b1),
59 .ce(1’b1),
60 .in(addr_in),
61 .out(addr_out));
62
63 endmodule
Moduł przyjmuje dwa parametry. K to liczba bitów przypadająca na reprezentację liczb, a N to liczba bitów adresu. Następnie w liniach 14…23 znajdziemy wejścia i wyjścia.
Pierwszy blok always_ff realizuje obliczanie modułu części rzeczywistej i ułamkowej. Dzięki zastosowaniu operatora ?:, implementacja całej funkcji mieści się w pojedynczej linii. Drugi blok (37…41) oblicza oba warianty nawiasu z równania (30). Następnie w wierszach 43…44 zrealizowany jest multiplekser, wybierający jedną z dwóch obliczonych wartości. Ostatni blok (46…47) to mnożenie przez 15/16.
Na samym końcu znajdziemy jeszcze dwie instancje linii opóźniającej. Pierwsza z nich, z resetem, obsługuje sygnał valid, a druga (bez resetu) adres.
Znamy już implementację, teraz przejdźmy do jej sprawdzenia. Kod testów znajduje się na listingu 11.
40 initial begin
41 valid_in = 1’b0;
42 rst = 1’b0;
43 #100ns @(negedge clk);
44 rst <= 1’b1;
45 valid_in = 1’b1;
46 for (int i = 0; i < C; i++) begin
47 d_re = in_re[i];
48 d_im = in_im[i];
49 addr_in = i;
50 @(posedge clk);
51 end
52 valid_in = 1’b0;
53 end
66 always_ff @(posedge clk) begin
67 if (!rst) begin
68 rms = 0;
69 i = 0;
70 end
71 if (valid_out) begin
72 abs_sim = $sqrt(in_re[i]**2 + in_im[i]**2);
73 $display("s: %.2f, h: %.2f, diff: %.2f", abs_sim, abs, abs_sim – abs);
74 rms += $sqrt((abs_sim – abs)**2);
75 i <= i + 1;
76 end
77 if (i == C) begin
78 rms = $sqrt(rms/N);
79 $display("RMS of error is %.1f", rms);
80 $stop;
81 end
82 end
Symulacje uruchamiamy, wywołując w programie ModelSim polecenie:
do abs_sim.do
Uzyskane przebiegi pokazuje rysunek 23. Na końcowy błąd składa się zarówno niedokładność algorytmu „alfa max beta min”, jak i błąd kwantyzacji (listing 12).
# s: 22.36, h: 24.00, diff: -1.64
# s: 22.36, h: 24.00, diff: -1.64
# s: 10.00, h: 10.00, diff: 0.00
# s: 20.00, h: 19.00, diff: 1.00
# s: 22.36, h: 24.00, diff: -1.64
# RMS of error is 1.4
Analizator widma – łączymy bloki
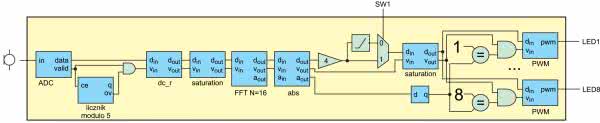
Mamy już wszystkie bloki, które pozwolą nam zbudować analizator widma dźwięku, którego schemat został pokazany na rysunku 24. Na początku widzimy tor składający się z przetwornika, decymacji oraz usuwania składowej stałej. Został on już wcześniej wykorzystany do zbierania próbek dźwięku i przesyłania ich poprzez port szeregowy. Tym razem trafiają one na 16 punktową transformatę Fouriera. Jej wyjście jest następnie mnożone przez 4. Jest to wartość dobrana empirycznie, tak aby uzyskane wartości, były widoczne na diodach.
Dodany jest także moduł obcinający wszystkie wartości mniejsze niż 10 (znowu dobrane eksperymentalnie). Można go włączać za pomocą przełącznika na płytce. Dalej znajdziemy kolejny blok saturacji (na wszelki wypadek) oraz 8 generatorów sygnału PWM. Każdy z nich steruje jasnością pojedynczej diody LED.
Aby generatory przyjmowały tylko odpowiednie wartości. Sygnał valid będzie dodatni jedynie, gdy adres próbki jest zgodny z „adresem diody”.
Zastanówmy się teraz, co zobaczymy na diodach. Częstotliwość próbkowania naszego ADC jest ustawiona na fp=10 kHz. Oznacza to, że rozdzielczość naszej transformaty to:
(32)
Próbka o adresie zero odpowiada częstotliwości 0 Hz (tak zwane DC). Ponieważ na wejściu mamy filtr usuwający składową stałą, jej wartość nie jest interesująca. Na diodach będzie prezentowana amplituda próbek od 1 do 8. Odpowiadają one częstotliwością: 625 Hz, 1250 Hz, …, 5 kHz.
Próbki o adresach od 9 do 15 odpowiadają częstotliwościom ujemnym. Ponieważ nasz wejściowy sygnał jest rzeczywisty, ich wartość będzie równa sprzężeniu wartości otrzymanej dla częstotliwości dodatniej.
Jako sygnał testowy możemy wykorzystać wygenerowany już przez nas świergot (11_dc_r\parse\chirp_0_5.mp3). Aby dowiedzieć się, czego możemy się spodziewać, najpierw możemy policzyć transformatę Fouriera dla zebranych wcześniej danych.
Pomoże nam w tym kod Python-owy z lisitngu 13. Zdefiniowaliśmy funkcję fft_time, która przyjmuje rozmiar transformaty oraz wektor próbek.
01 def fft_time(N, xn):
02 N_2 = int(N / 2)
03 k = int(len(xn)/N)
04 X = np.zeros([N_2, k])
05 for i in range(k):
06 X[:,i] = (np.abs(np.fft.fft(xn[N*i:N*(i+1)])))[0:N_2] / N
07 return X
08
09 X_16 = fft_time(16, xn)
10 plt.imshow(X_16, aspect=’auto’, cmap=matplotlib.cm.jet)
11 plt.colorbar()
Zostaje on podzielony na nienachodzące na siebie fragmenty o długości N. Dla każdego z nich zostaje policzone FFT. Jako wyjście dostajemy dwuwymiarową tablicę kolejnych transformat. Następnie możemy ją wyrysować za pomocą funkcji imshow.
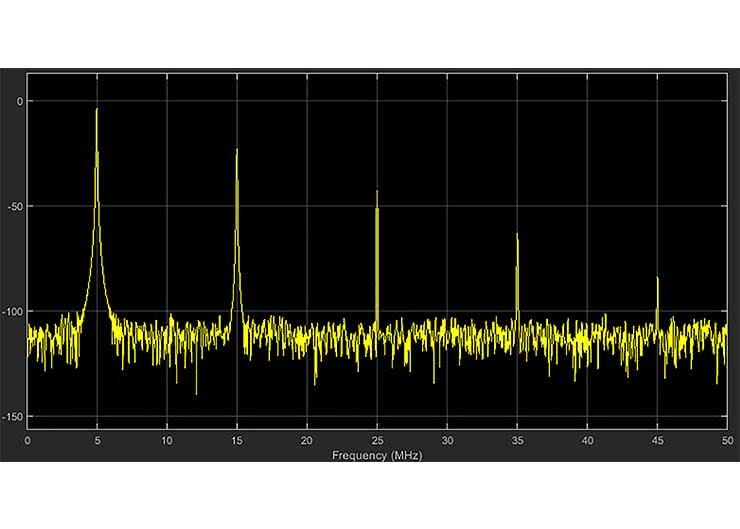
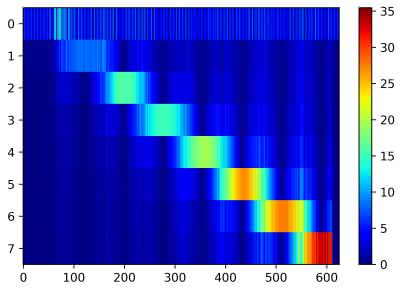
Na rysunku 25 zostały pokazane wartości uzyskane dla zarejestrowanego sygnału typu chirp. Widzimy, że wyraźny prążek otrzymujemy, gdy chwilowa częstotliwość jest bliska którejś z naszych częstotliwości bazowych. W przeciwnym przypadku jest on rozmyty. Zjawisko to nosi nazwę „wycieku widma”. Jest ono największe, gdy wejściowy sygnał ma częstotliwość, znajdującą się dokładnie w połowie pomiędzy częstotliwościami bazowymi.
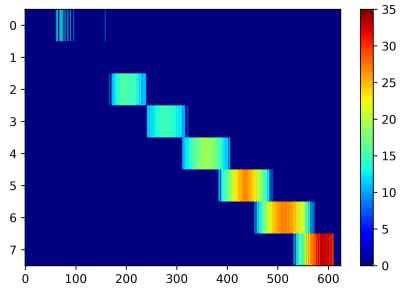
Naiwną metodą rozwiązania tego problemu, jest wyzerowanie wartości niższych niż przyjęty próg. Po to jest właśnie funkcja, którą będziemy uruchamiali za pomocą przełącznika SW1. Eksperymentalnie dobrałem próg równy 10. Uzyskany efekt pokazuje rysunek 26.
Znacznie lepszą metodą radzenia sobie z wyciekiem widma jest zastosowanie tak zwanego okienkowania, ale jest bardziej skomplikowana. Implementacja została pokazana na listingu 14.
010 module fft_top #(
011 parameter F = 8000000,
012 parameter LED = 8
013 ) (
014 input wire clk,
015 input wire rst,
016 input wire sw1,
017 output logic [LED-1:0]led
018 );
043 always_ff @(posedge clk)
044 sw1_r <= sw1;
080 saturation #(.N_IN(N_ADC), .N_OUT(K)) sat (
081 .in(bus_dcr),
082 .out(bus_fft));
083
084 fft #(.K(K), .N(N)) fft_inst (
085 .clk(clk),
086 .rst(rst),
087 .d_in_re(bus_fft.data),
088 .d_in_im(‘0),
089 .valid_in(bus_fft.valid),
090 .d_out_re(fft_re),
091 .d_out_im(fft_im),
092 .addr(fft_addr),
093 .valid_out(fft_valid));
094
095 abs #(.K(K), .N(LOG_N)) abs_inst (
096 .clk(clk),
097 .rst(rst),
098 .d_re(fft_re),
099 .d_im(fft_im),
100 .valid_in(fft_valid),
101 .addr_in(fft_addr),
102 .abs(abs),
103 .addr_out(abs_addr),
104 .valid_out(abs_valid));
105
106 assign bus_abs.valid = abs_valid;
107 assign bus_abs.data = (sw1 || abs > 10) ? 4 * abs : ‘0;
108 always_ff @(posedge clk)
109 sat_addr <= abs_addr;
110
111 saturation #(.N_IN(K+2), .N_OUT(K)) sat1 (
112 .in(bus_abs),
113 .out(bus_sat));
114
115 generate
116 genvar i;
117 for (i = 0; i < LED; i++) begin : PWM
118 StreamBus pwm_bus(clk, rst);
119 assign pwm_bus.valid = bus_sat.valid & (sat_addr == (i + 1));
120 assign pwm_bus.data = bus_sat.data;
121 pwm #(.MAX(2**K-1)) pwm_inst (
122 .bus(pwm_bus),
123 .ce(1’b1),
124 .pwm(led[i]));
125 end
126 endgenerate
Nasz moduł ma trzy wejścia: zegar, reset, przełącznik sw1 oraz jeden wektor wyjściowy. Steruje on wszystkimi ośmioma diodami, dostępnymi na płytce Rysino. Kod jest stosunkowo prosty. Większość miejsca zajmują instancje kolejnych bloków. Należy jedynie uważać, aby zmienne użyte do ich połączenia miały odpowiednią długość.
Progowanie zrealizowane jest w linii 107 za pomocą operatora ?:. Osiem instancji generatora sygnału PWM zostało umieszczonych w bloku generate (wiersze 115…126). Do ich zbudowania wykorzystujemy pętle for.
Testbench jest bardzo podobny jak w przypadku projektu z modułem dc_r. Używamy tutaj symulacyjnej wersji bloku ADC, z tym samym plikiem z danymi. Ponieważ przerwy między kolejnymi odczytanymi danymi są dosyć długie, stworzono dodatkowe zmienne, do których wartości są zapisywanie jedynie, gdy odpowiadające im sygnały valid są ustawione. Odpowiedzialny za to fragment kodu pokazuje listing 15.
38 always_ff @(posedge clk) begin
39 if (dut.adc_valid_out)
40 adc_data_out <= dut.adc_data_out;
41 if (dut.bus_dcr.valid)
42 data_dc <= dut.bus_dcr.data;
43 if (dut.bus_fft.valid)
44 data_fft_in <= dut.bus_fft.data;
45 if (dut.fft_valid) begin
46 fft_re <= dut.fft_re;
47 fft_im <= dut.fft_im;
48 fft_addr <= dut.fft_addr;
49 end
50 if (dut.abs_valid)
51 abs[dut.abs_addr] <= dut.abs;
52 end
Symulację uruchamiamy poleceniem:
do fft_top_sim.do
Zachęcam do prześledzenia uzyskanych wyników.
Teraz możemy (w końcu) przystąpić do testów w sprzęcie. Otwieramy środowisko Quartus, ładujemy projekt 13_fft/fft.qpf i uruchamiamy jego budowę. Projekt zajmuje 10 z 40 dostępnych mnożarek oraz 1074 (czyli nieco ponad jedną czwartą) z dostępnych elementów logicznych. Zużycie pamięci jest mniejsze niż 1%.
Kiedy mamy gotowy wsad, możemy przejść do testów w sprzęcie. Podłączamy mikrofon (dokładnie tak samo jak przy testowaniu bloku dc_r) i wgrywamy wygenerowany bitstream. W ramach testu, możemy przyłożyć mikrofon do głośnika i generować z niego sygnały sinusoidalne o różnej częstotliwości. Zmieniając pozycję suwaka SW1, możemy włączać i wyłączać pogowanie. Efekt uzyskany dla kilku tonów oraz świergotu od 0 do 5 kHz pokazuje film [3].
Podsumowanie
Rozpoczęliśmy od teoretycznych podstaw dyskretnej transformaty Fouriera. Następnie poznaliśmy sprytny sposób jej obliczania, który pozwala zmniejszyć złożoność obliczeniową z poziomu N2 na Nlog2N. Po wyprowadzeniu algorytmu przygotowaliśmy jego sprzętową implementację.
Następnie zapoznaliśmy się z algorytmem „alfa max beta min” pozwalającym aproksymować wartość modułu liczby zespolonej. Na końcu połączyliśmy wszystkie stworzone bloki w analizator widma dźwięku.
Rafał Kozik
rafkozik@gmail.com
Przypisy:
[1] Repozytorium z przykładami, http://bit.ly/33uYPxs
[2] Lyons R.G., Wprowadzenie do cyfrowego przetwarzania sygnałów, Wydawnictwo Komunikacji i Łączności, Warszawa 2010
[3] Film prezentujący działanie FFT, https://bit.ly/35H0yTp

 Zaloguj
Zaloguj