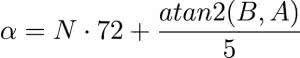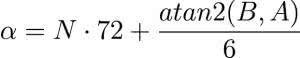Precyzyjny pomiar kąta przydatny jest w wielu urządzeniach – ploterach, maszynach CNC, robotach i wielu innych. Konstrukcja ta jest jednocześnie na tyle prosta, że wszystkie komponenty urządzenia mogą być bez problemu osadzone w przegubach robota czy przy serwomotorze sterującym urządzeniem.
Szacunkowy koszt tego enkodera, bez modułu Arduino, to poniżej 10 dolarów (około 40 zł).
Potrzebne elementy
Do zbudowania układu potrzebne:
- 10 magnesów neodymowych o średnicy 6 mm i wysokości 3 mm,
- dwa liniowe czujniki Halla 49E/AH49E,
- śruba M4×20 mm,
- nakrętka M4,
- goldpiny,
- przewody połączeniowe,
- elementy wydrukowane w 3D (opisane dalej).
Hallotrony AH49E to proste elementy analogowe, dostarczane w obudowach TO-92 i SOT-23-3. Jeśli mamy problem z ich zakupem, a mamy dostęp do modułów KY-024, to można hallotrony pozyskać z tych płytek (są one znacznie częściej dostępne w sklepach dla hobbystów niż sensory Halla, jako elementy dyskretne).
Układ elektroniczny
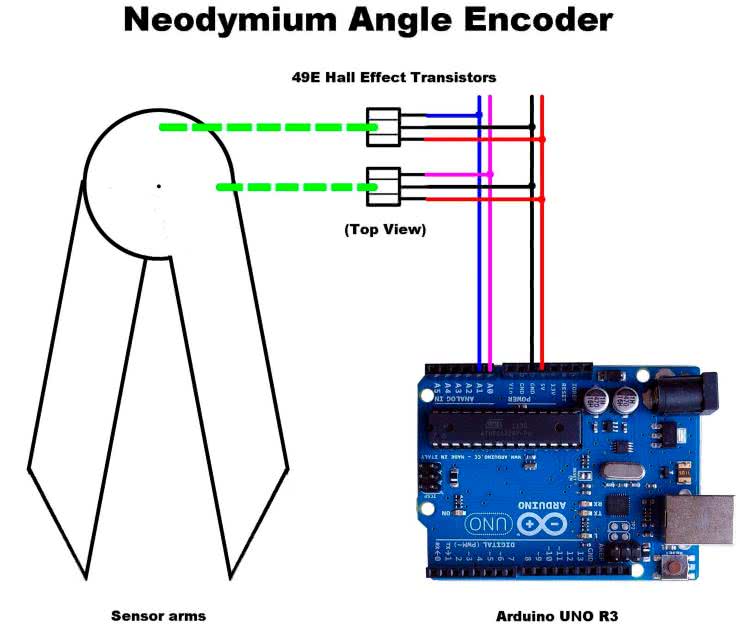
Schemat obwodu enkodera pokazano na rysunku 1. Jest on bardzo prosty – dwa sensory pola magnetycznego podłączone są do masy (linia czarna) i zasilania – 5 V (linia czerwona). Sygnały wyjściowe z sensorów (linia niebieska i fioletowa) podłączone są do wejść analogowych A0 i A1 modułu Arduino.
W przypadku braku pola magnetycznego napięcia wyjściowe na pinach A0 i A1 z każdego sensora wynoszą Vcc/2 = 2,5 V, w przypadku zasilania układu z linii 5 V (maksymalne napięcie zasilania sensora to 8 V). Odpowiada to odczytowi przetwornika analogowo-cyfrowego (ADC) w Arduino równemu 512 (1023/2 – przetwornik w module Arduino jest 10-bitowy).
Zasada działania
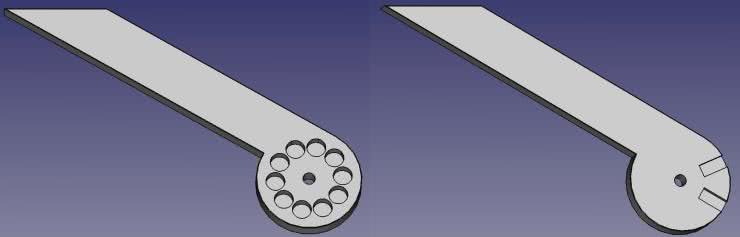
Na rysunku 2 pokazano 10 magnesów ułożonych w okrąg w jednym z wydrukowanych elementów.
Bieguny magnesów skierowane są w osi góra–dół. Ułożone są naprzemiennie. Pole magnetyczne tych magnesów pokazane jest na rysunku 3, gdzie nad magnesami umieszczono wizualizator pola magnetycznego w postaci cienkiej płytki ze specjalnym materiałem.
Żółty kolor pokazuje obszary z najsłabszym polem, gdzie zmiana wartości na hallotronie będzie najsłabsza. Kolor niebieski reprezentuje z kolei maksimum pola, czyli miejsca, gdzie czujnik Halla wskazywać będzie najwyższą amplitudę. Powodem, dla którego żółte obszary są okrągłe, jest to, że linie pola z każdego z północnych biegunów magnetycznych wychodzą we wszystkich kierunkach. Płytka do wizualizacji pola magnetycznego nie jest wymagana podczas konstruowania tego układu.
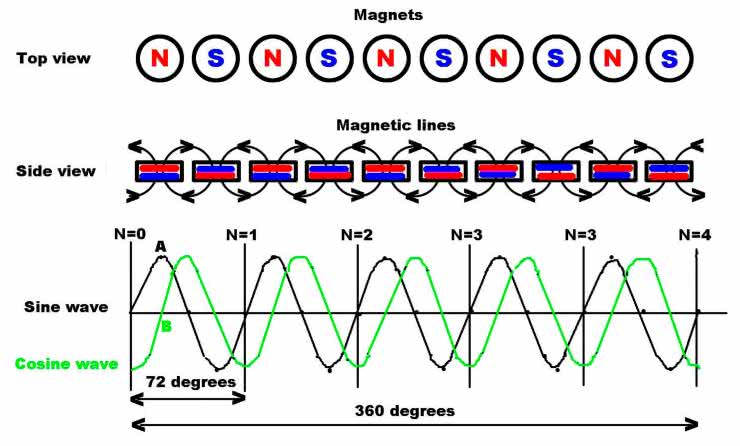
Zastosowany układ magnesów skutkuje podzieleniem okręgu na 10 segmentów, każdy po 36°. Gdy jeden czujnik trafi na środek segmentu, drugi jest pomiędzy nimi. Dzięki temu, w czasie obrotu, jeśli jeden z sensorów na wyjściu będzie miał przebieg sinusoidalny, to na wyjściu drugiego zaobserwujemy cosinus. Zobrazowano to na rysunku 4.
Podsumowując:
- w układzie jest parzysta liczba magnesów,
- każde 2 naprzemiennie ułożone magnesy wytwarzają 1 falę sinusoidalną,
- przy 10 magnesach otrzymujemy 5 pełnych przebiegów sinusoidalnych na obrót wału,
- każda fala sinusoidalna reprezentuje obrót wału o 360/5=72°,
- każda połowa cyklu to 72/2=36°,
- odległość między maksimum a minimum wynosi 36/2=18°, co oznacza, że czujniki muszą być oddalone od siebie o N*36+18°. W projektowanym enkoderze zadano N = 1, więc czujniki są oddalone od siebie o 54°. Ustawienie N=0 nie było możliwe ze względu na wielkość czujników.
Wzór na obliczenie kąta wału jest zatem następujący:
gdzie:
- n – liczba ukończonych fal sinusoidalnych,
- a – wielkość przebiegu sinusoidalnego w dowolnym momencie (amplituda mierzona przez sensor Halla),
- b – wielkość przebiegu cosinus w dowolnej chwili (amplituda mierzona przez sensor Halla),
- 5 – liczba fal sinusoidalnych w 360°, w tym przypadku 10 magnesów podzielone na 2. Dla innej liczby magnesów możemy uzyskać inny parametr.
Uwagi praktyczne
Pomiędzy magnesami a sensorami z efektem Halla wymagana jest przekładka, która zapobiegnie nasyceniu się hallotronów. Optymalny odstęp występuje wtedy, gdy odczyty z ADC ciągle się zmieniają (tj. nigdy nie pozostają na stałym poziomie) podczas obracania magnesów. Grubość elementu dystansowego na poziomie 2,7 mm okazała się optymalna dla magnesów, z jakich korzystał autor.
Liczba cykli sinusa musi być śledzona w oprogramowaniu. Możliwe są inne kombinacje magnesów, pod warunkiem że pary magnetyczne podzielą się równomiernie na 360°. Na przykład 12 magnesów wytworzy 6 cykli, z których każdy reprezentuje obrót wału o 60°, z przejściami przez zero, co 30°. W tym przypadku odległość między maksimum a minimum wynosi 30/2=15°, co oznacza, że czujniki muszą być oddalone od siebie o N*30+15°. W tym przykładzie kąt wału będzie wynosił:
Uwagi
Maksymalna i minimalna zmiana wyjścia sensora Halla zależy od orientacji struktury czujnika Halla względem kierunku pola magnetycznego. W przypadku tego projektu sensory leżą płasko w drugiej części z druku 3D, co oznacza, że największą zmianę sygnału wyjściowego obserwuje się, gdy znajdują się one bezpośrednio nad magnesami.
Jeśli element z efektem Halla zostanie obrócony o 90°, wówczas minimalna zmiana napięcia wyjściowego nastąpi nad magnesami, a maksymalny sygnał pomiędzy nimi.
W przypadku braku pola magnetycznego, odczyty Arduino ADC dla A0 i A1 będą bliskie 512. Odczyty te będą odchylać się w czasie ruchu magnesów po obu stronach wartości 512 o około ±300 (w przybliżeniu, w zależności od odległości i użytych magnesów). Idealnie by było, aby dynamika osiągała ±500.
Elementy z druku 3D
W technologii druku 3D wykonano trzy elementy: dwa ramiona (pokazane na rysunku 5) oraz przekładkę.
Projekty wszystkich elementów udostępnione są na stronie z projektem w formacie plików STL. Każda część została wydrukowana na drukarce 3D Voxelab Aquila przy użyciu filamentu PLA o średnicy 1,75 mm. Rozmiar zastosowanej dyszy to 0,4 mm przy wysokości warstwy 0,2 mm.
Oprogramowanie
Listing kodu Arduino neodymium_angle_encoder.ino pokazano na listingu 1. Szkic kopiujemy do Arduino IDE, kompilujemy i wgrywamy do Arduino. Od teraz, po uruchomieniu moduł mierzy wartości i oblicza kąt. Wyniki przesyłane są do komputera przez interfejs szeregowy w czytelnym dla człowieka formacie. Można zmodyfikować ten fragment programu, jeśli chcemy, aby moduł współpracował z innym systemem.
#define RAD_TO_DEG 57.295779513082320876798154814105
const byte ADC0 = A0;
const byte ADC1 = A1;
const byte Switch = 8;
float A, Amax, Amin, Amid, Apeak;
float B, Bmax, Bmin, Bmid, Bpeak, Bnormal;
// 360 dstopni odpowiada obrotowi osi o 72 stopnie
float RawAngle;
// identyfikacja ćwiartki
int QuadrantNumber = 0;
// zmienna do śledzenia liczby obrotów
int PreviousQuadrantNumber = 0;
// liczba okresów sinusa
int N = 0;
// kąt początkowy
float StartAngle = 0;
// kąt wytarowany w oparciu o kąt początkowy
float TaredAngle = 0;
// kąt całkowity
float ShaftAngle = 0;
unsigned long Timer;
const unsigned long Next_sample = 1000L;
void setup() {
Serial.begin(115200);
Serial.flush();
while (Serial.available()) Serial.read();
pinMode (Switch, INPUT_PULLUP);
pinMode(ADC0, INPUT);
pinMode(ADC1, INPUT);
// Jesli pin 8 na masie, uruchamia kalibracje
if (!digitalRead(Switch)) {
calibrate();
}
// Pobiera surowy kąt
StartAngle = raw_angle();
Timer = millis() + Next_sample;
}
void loop() {
RawAngle = raw_angle();
TaredAngle = tare(RawAngle);
// Zlicza liczbę skompletowanych okresów
N = numberOfSinewaves();
ShaftAngle = N * 72 + TaredAngle/5;
if (millis() >= Timer) {
Timer += Next_sample;
Serial.print("Shaft Angle: ");
Serial.print(ShaftAngle);
Serial.println(" degrees");
}
}
// Mierzy kąt w zakresie 0..72 w segmencie
float raw_angle() {
float adc0;
float adc1;
adc0 = (float)analogRead(ADC0);
adc1 = (float)analogRead(ADC1);
A = adc0 – Amid;
B = (adc1 – Bmid) * Bnormal;
float angle = atan2(B, A) * RAD_TO_DEG;
// Dla kąta pomiędzy 180 a 360
// potrzebna jest negacja atan2
if (angle < 0) angle += 360;
return angle;
}
float tare(float angle) {
// This tares the position
float taredAngle = angle – StartAngle;
// If the calculated angle is negative,
// we need to "normalize" it
if (taredAngle < 0) {
// correction for negative numbers
// (i.e. -15 becomes +345)
taredAngle = taredAngle + 360;
}
return taredAngle;
}
int numberOfSinewaves() { // Zliczanie okresów sinusa
static int sinewaves = 0;
// I ćwiartka
if (TaredAngle >= 0 && TaredAngle <= 90) {
QuadrantNumber = 1;
}
// II ćwiartka
if (TaredAngle > 90 && TaredAngle <= 180) {
QuadrantNumber = 2;
}
// III ćwiartka
if (TaredAngle > 180 && TaredAngle <= 270) {
QuadrantNumber = 3;
}
// IV ćwiartka
if (TaredAngle > 270 && TaredAngle < 360) {
QuadrantNumber = 4;
}
// Czy nastąpiła zmiana ćwiartki
if (QuadrantNumber != PreviousQuadrantNumber) {
if (QuadrantNumber == 1 && PreviousQuadrantNumber == 4) {
sinewaves++;
}
if (QuadrantNumber == 4 && PreviousQuadrantNumber == 1) {
sinewaves--;
}
// Aktuializacja ćwiartki
PreviousQuadrantNumber = QuadrantNumber;
}
return sinewaves;
}
void calibrate() { // Kalibracja
Amax = -10000.0;
Amin = 10000.0;
Bmax = -10000.0;
Bmin = 10000.0;
while (!digitalRead(Switch)) {
A = (float)analogRead(ADC0);
B = (float)analogRead(ADC1);
Amax = max(Amax, A);
Amin = min(Amin, A);
Bmax = max(Bmax, B);
Bmin = min(Bmin, B);
Amid = (Amax + Amin)/2;
Apeak = Amax – Amid;
Bmid = (Bmax + Bmin)/2;
Bpeak = Bmax – Bmid;
Bnormal = Apeak/Bpeak;
Serial.print(" Amax: "); Serial.println(Amax);
Serial.print(" Amin: "); Serial.println(Amin);
Serial.print(" Amid: "); Serial.println(Amid);
Serial.print(" Apeak: "); Serial.println(Apeak);
Serial.print(" Bmax: "); Serial.println(Bmax);
Serial.print(" Bmin: "); Serial.println(Bmin);
Serial.print(" Bmid: "); Serial.println(Bmid);
Serial.print(" Bpeak: "); Serial.println(Bpeak);
Serial.print("Bnormal: "); Serial.println(Bnormal);
Serial.println(" ");
delay(100);
}
}
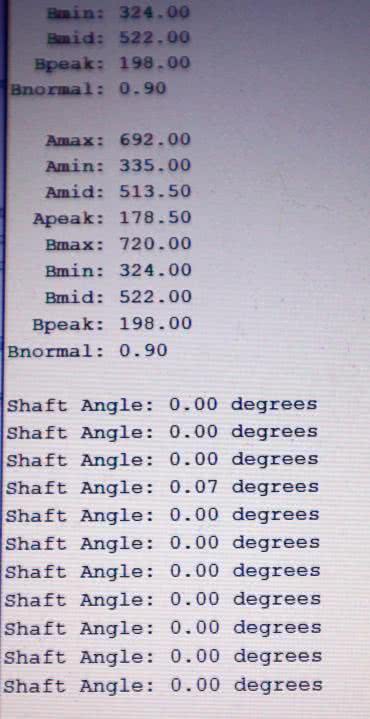
Jednak, aby układ poprawnie i dokładnie mierzył kąt, należy go najpierw skalibrować. W tym celu wykonujemy następujące czynności:
- podłączamy przewód między wyprowadzenie nr 8 Arduino a masę,
- obracamy ramię magnesu kilka razy, aż odczyty na wyświetlaczu będą stałe,
- kopiujemy odczyty wyświetlacza do pasujących zmiennych w nagłówku Arduino,
- zdejmujemy zworkę,
- ponownie kompilujemy kod i przesyłamy go do Arduino.
Dalsza kalibracja nie powinna być konieczna, wszystkie kąty odnoszą się do pozycji ramion enkodera. Na rysunku 6 pokazano odczyty przy kalibracji oraz przy pomiarach kąta.
Przejście następuje, gdy przewód połączeniowy z wyprowadzenia nr 8 Arduino do masy zostanie usunięty. Na rysunku 7 pokazano konfigurację testową, jaką autor przygotował do pomiaru dokładności enkodera. Linie radialne są rozmieszczone co 10°.
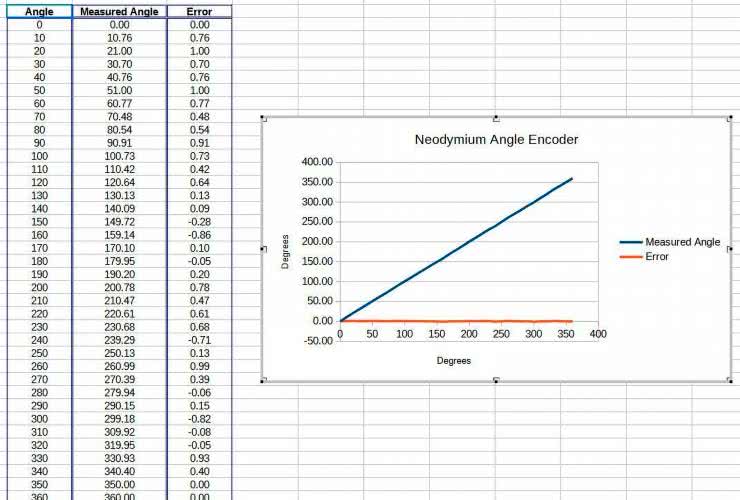
Na rysunku 8 pokazano wykres zależności błędu odczytu kąta od mierzonego kąta. Wszystkie zmierzone wartości mieszczą się w zakresie 1° od rzeczywistego kąta.
Podsumowanie
Zaprezentowany projekt pokazuje, w jaki sposób zbudować relatywnie precyzyjny enkoder kątowy przy użyciu jedynie 10 magnesów neodymowych i dwóch sensorów z efektem Halla. Zmierzona dokładność enkodera mieści się w granicach 1°. Łatwo można ją podnieść, dodając więcej magnesów lub zmieniając przetwornik analogowo-cyfrowy w układzie na zewnętrzny, o większej rozdzielczości.
Konstrukcja została zaprojektowana tak, aby komponenty mogły być łatwo osadzone np. w przegubach ramienia robota czy w serwomotorze plotera. Wykonanie takiego enkodera jest bardzo tanie i nie powinno przekraczać 40 zł (z wyłączeniem modułu Arduino). Po zmianach w kodzie mikrokontroler może jednocześnie obsługiwać większą liczbę takich enkoderów – jest to ograniczone jedynie liczbą wejść analogowych.
Nikodem Czechowski, EP
Źródło:
https://www.instructables.com/Neodymium-Angle-Encoder

 Zaloguj
Zaloguj