Zbieranie danych
Do śledzenia pozycji dłoni użyjemy czujnika Sharp GP2D12 (fotografia 1). Cały eksperyment powinien jednak działać także z innymi sensorami (oczywiście po przygotowaniu własnych danych uczących).
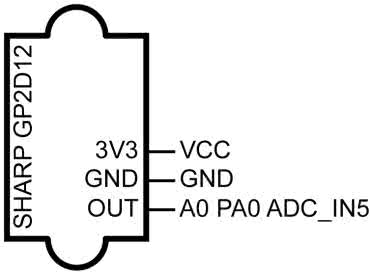
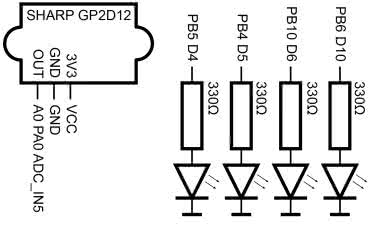
Sposób podłączenia czujnika do zestawu deweloperskiego Nucleo-L476RG pokazuje rysunek 1.
Czujnik jest zasilany z płytki, a jego wyjście jest podłączone do złącza A0. Złożony model prezentuje fotografia 2. Na czujnik została nałożona papierowa rura. Zapobiega ona przyłożeniu ręki zbyt blisko czujnika, którego zakres pracy wynosi od 10 do 80 cm.
Program zbierający dane znajduje się w repozytorium [1]. Został przygotowany w STM32CubeIDE. Odczyt z przetwornika cyfrowo-analogowego wyzwalany jest przepełnieniem licznika/czasomierza (Timer) numer 4. Następuje ono co 50 ms. Zakończenie pomiaru wyzwala przerwanie, w którym następuje wysłanie zebranych danych poprzez interfejs UART.
Postanowiłem przygotować cztery gesty wykonywane dłonią nad czujnikiem. Obrazowo określiłem je jako:
- z dołu do góry,
- z góry na dół,
- koziołkowanie,
- machanie.
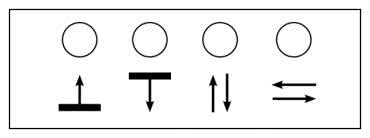
Są one zaprezentowane na filmie [2] oraz symbolicznie pokazane za pomocą piktogramów na rysunku 2.
Dla każdego z czterech gestów zapisałem przebieg z dwudziestoma powtórzeniami. Dane można zebrać za pomocą dowolnego monitora portu szeregowego. Zebrałem także około 40 sekund przebiegu z czujnika, gdy nie był pokazywany żaden gest. Następnie w edytorze tekstowym usunąłem znaki nowej linii. Zebrane dane wkleiłem do notatnika Jupyter [3] jako tablicę w języku Python. Tworzą one dwuwymiarową tablicę d, której kolejne wiersze odpowiadają po kolei gestom z tablicy g:
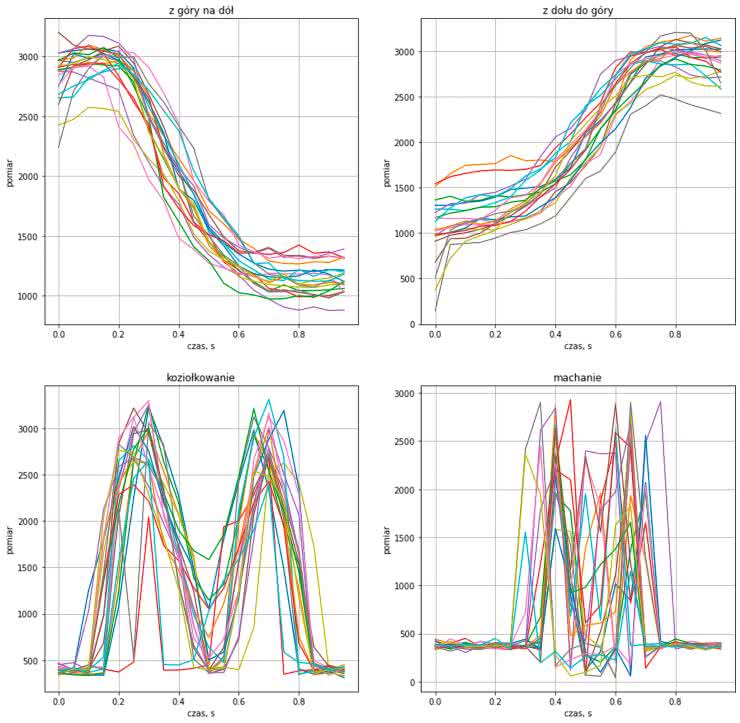
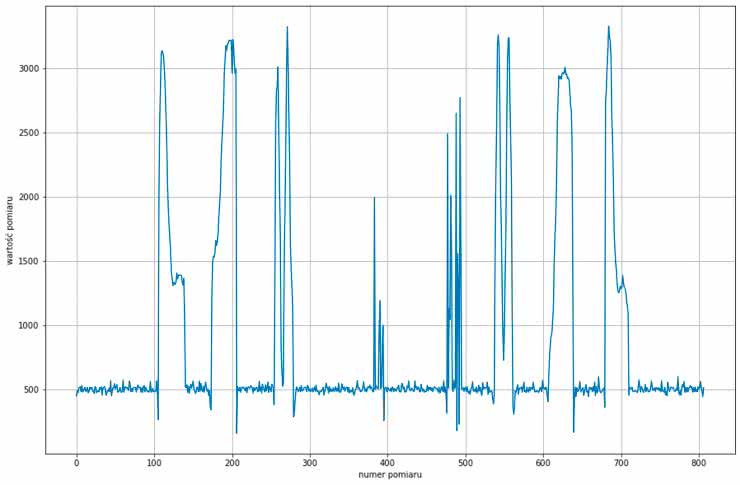
Odstęp pomiędzy kolejnymi próbkami wynosi T=0.05 sekundy. Aby zorientować się, jakie dane zebraliśmy, przebiegi zostały wyrysowane na wykresach pokazanych na rysunku 3.
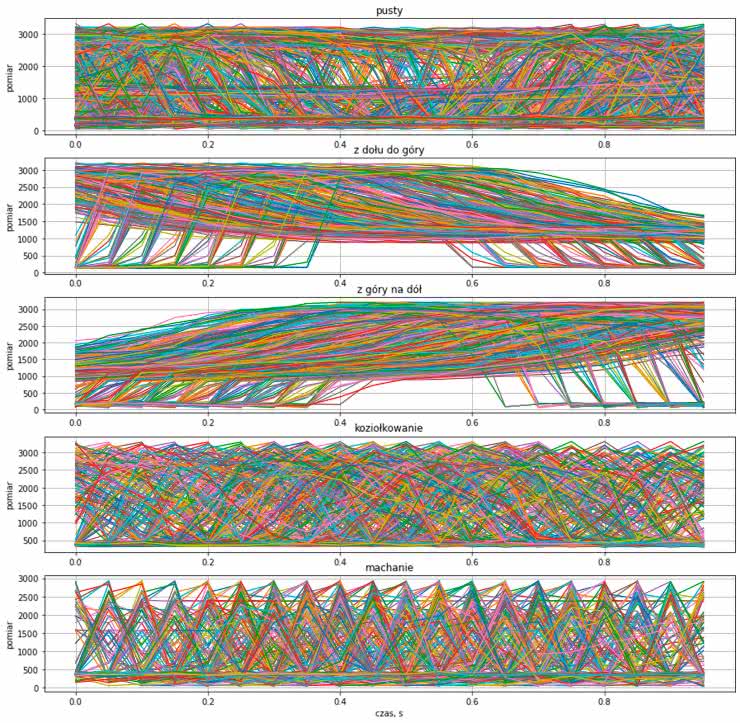
Przyjąłem, że pojedyncze okno detekcji będzie miało długość 1 sekundy, czyli 20 próbek. Wektory zawierające kolejne 20 próbek będą podawane na wejście sieci neuronowej, która będzie rozstrzygała, czy zawierają one jakiś istotny sygnał. Dla każdego z gestów został powiększony pojedynczy przykład o długości 20 próbek, które prezentuje rysunek 4.
Nasz czujnik zwraca wartość odwrotnie proporcjonalną do odległości, więc wyższa wartość oznacza rękę w bliższej, a niższa w dalszej odległości od czujnika. Długość wektora równa 20 próbkom została wybrana dość arbitralnie. Dociekliwi czytelnicy mogą sprawdzić, jak zmiana tego parametru wpłynęłaby na uzyskane wyniki.
Zbiór uczący
Najbardziej czasochłonną częścią jest przygotowanie danych treningowych. Dla każdego przypadku musimy znaleźć próbkę, którą uznamy za początek gestu. Ja zrobiłem to ręcznie, pomagając sobie funkcją plot_start(data, start, i_min=0). Przyjmuje ona trzy parametry:
- wektor danych dla jednego z zebranych gestów,
- wektor początków kolejnych gestów,
- element wektora start, od którego ma zacząć rysowanie.
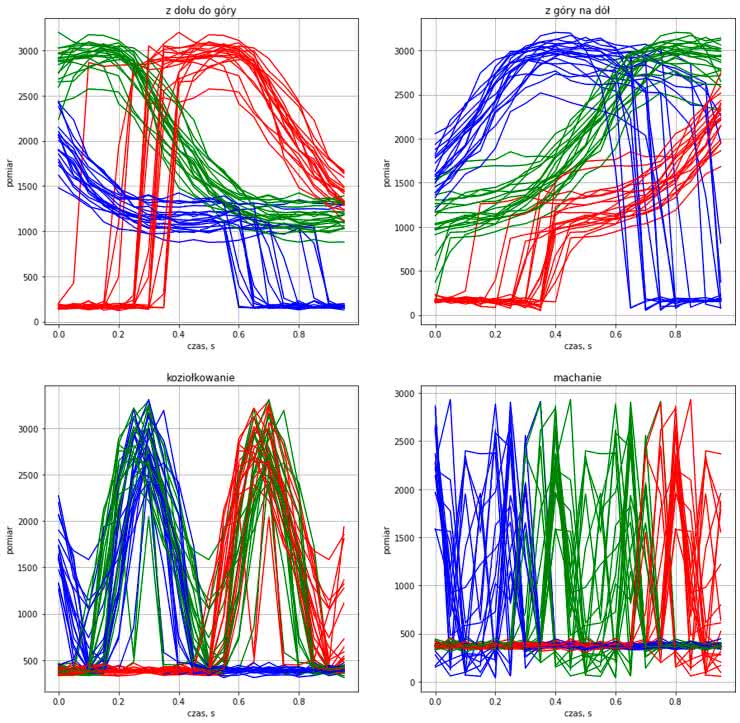
Zwraca ona wykres z wyrysowanymi (jedne na drugich) kolejnymi gestami. Możemy wywoływać ją, dobierając kolejne wartości wektora start i obserwować, czy kolejne wykresy są do siebie podobne. Jeżeli plątanina krzywych jest zbyt duża, możemy zmniejszyć liczbę rysowanych przebiegów, zwiększając parametr i_min. Bardziej zaradni czytelnicy mogą przygotować skrypt, który wyznaczy orientacyjne wartości wektora start na podstawie przekroczenia przez wartość określonych progów. Uzyskane przeze mnie krzywe prezentuje rysunek 5.
Trudno jest jednoznacznie ustalić, gdzie zaczyna się, a gdzie kończy dany gest. Możemy więc przyjąć parametr K, mówiacy o tym, o ile próbek możemy przesunąć okno pomiarowe (w przód albo tył) i nadal uznać je za zawierające gesty. Wyznaczyłem wykresy zawierające przebiegi ze skrajnych położeń oraz centralną wartość dla różnych parametrów i zdecydowałem się na wartość 8. Lecz jest to kolejny metaparametr naszego modelu, z którym możemy eksperymentować. Uzyskane przesunięcia obrazuje rysunek 6.
Przy pierwszym podejściu do nauki sieci jako przykładu gestów użyłem tylko przebiegu z niezasłoniętego czujnika, który znamy z rysunku 3. Kod, który posłużył do utworzenia zbioru treningowego i walidacyjnego, prezentuje listing 1. Najpierw do zbiorów treningowego i walidacyjnego zostały dodane wszystkie ciągi z nagranego niezasłanianego czujnika. Do zbioru walidacyjnego trafiała co 10. próbka. Następnie do zbiorów zostały dodane wszystkie ciągi zawierające gesty, czyli te zaczynające się o ±K próbek względem wyznaczonych początków gestów.
v1_data_t = []
v1_label_t = []
v1_data_v = []
v1_label_v = []
for i in range(len(d[0])-N):
d_tmp = d[0][i:i+N]
l_tmp = 0
if i % 10 != 0:
v1_data_t.append(d_tmp)
v1_label_t.append(l_tmp)
else:
v1_data_v.append(d_tmp)
v1_label_v.append(l_tmp)
for i in range(len(s)):
for j in range(len(s[i])):
for k in range(-K, K):
d_tmp = d[i+1][s[i][j]+k:s[i][j]+k+N]
l_tmp = i+1
if j % 10 != 0:
v1_data_t.append(d_tmp)
v1_label_t.append(l_tmp)
else:
v1_data_v.append(d_tmp)
v1_label_v.append(l_tmp)
len(v1_data_t), len(v1_label_t), len(v1_data_v), len(v1_label_v)
Uczenie i walidacja
Do utworzenia modelu sieci i jej trenowania służy funkcja: train_model. Pierwsze cztery parametry opisują dane oraz etykiety zbiorów treningowego oraz uczącego. Jak widzimy na listingu 2, tworzy ona sieć przyjmującą wektor o długości 20.
def train_model(data_t, label_t, data_v, label_v, size=64, epochs=1000):
model = tf.keras.models.Sequential([
tf.keras.layers.Flatten(input_shape=(20, 1)),
tf.keras.layers.Dense(size, activation=’relu’),
tf.keras.layers.Dropout(0.2),
tf.keras.layers.Dense(5)
])
loss_fn = tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True)
model.compile(optimizer=’adam’,
loss=loss_fn,
metrics=[‘accuracy’])
model.fit(data_t, label_t, epochs=epochs, verbose=0)
model.evaluate(np.array(data_t), np.array(label_t), verbose=2)
model.evaluate(np.array(data_v), np.array(label_v), verbose=2)
return model
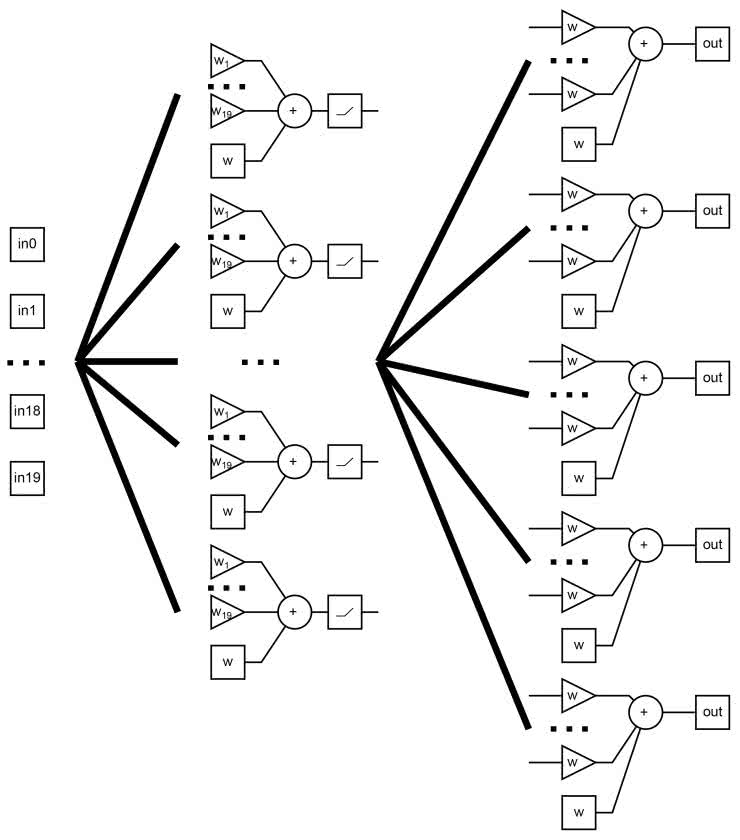
Schemat sieci widzimy na rysunku 7. Pierwsza warstwa jest złożona z size neuronów z funkcją aktywującą ReLU. Każdy z nich ma dwadzieścia wejść i przyjmuje pełny wektor wejściowy. Warstwa wyjściowa ma zawsze pięć neuronów: po jednym dla każdego z gestów oraz braku detekcji. Każdy z nich ma size wejść: przyjmuje wyjścia z każdego neuronu z poprzedniej warstwy. Warstwa wyjściowa ma liniową funkcję aktywacji.
Model jest trenowany przez epochs cykli. Dla przyśpieszenia podczas optymalizacji nie są wypisywane informacje o postępach. Dopiero na końcu zostanie wypisana dokładność dla zbioru treningowego i walidacyjnego. Dla pierwszego zestawu danych otrzymałem bardzo dobre wartości. Zarówno dla zbioru treningowego, jak i walidacyjnego dokładność wynosiła 100%, a błąd był rzędu 0,0005.
Postanowiłem przygotować test obrazujący bardziej realne warunki pracy sieci. Nagrałem przykład, gdzie po kolei prezentuję gesty: z dołu do góry, z góry na dół, koziołkowanie, machanie, machanie, koziołkowanie, z góry na dół, z dołu do góry. Pomiędzy każdym zachowuję około dziesięciu sekund przerwy (odmierzane za pomocą stopera). Wektor zebranych danych został przypisany do zmiennej test_data. Zebrane dane prezentuje rysunek 8.
Tutaj muszę się przyznać, że ja swoje eksperymenty wykonywałem w trochę innej kolejności niż w opisie. Gdy nagrywałem przebieg testowy, miałem już także sieć działającą w sprzęcie oraz model nauczony na rozszerzonych danych (o czym za chwilę). Występowało więc zjawisko, w którym sieć uczyła się na moich zapisanych gestach, a później ja uczyłem się wykonywać gesty, które rozumie sieć. Nie jest więc to pierwszy przebieg testowy, który zebrałem, ale już taki, dla którego prezentowałem gesty, których nauczyłem się „pod wymagania sieci”.
Następnie przygotowujemy drugą tablicę check zawierającą pary: numer próbki oraz gest, który się od niej rozpoczyna. Pierwszy element to oczywiście [0,0], czyli na początku mamy ciszę. Aby dokładniej wybrać punkty, możemy otworzyć wykres w osobnym oknie, gdzie możemy przybliżać jego fragmenty.
W tym celu odkomentowywujemy linie:
Po zakończeniu z powrotem przywracamy wykresy umieszczane w notatniku za pomocą polecenia:
Ocenę pracy modelu na przygotowanym ciągu realizuje funkcja test_on_data. Przyjmuje ona trzy parametry:
- zebrany ciąg próbek,
- miejsca rozpoczęcia się symboli,
- funkcję uruchamiającą testowany model na zebranych danych.
Funkcja zwraca trzy różne wskaźniki jakości:
- score - przyznaje +1 za poprawne wykrycie gestu bądź -1 za błędny gest albo wykrycie gestu, gdy czujnik był niezasłonięty,
- wrong - liczbę próbek, dla których model zwraca złą wartość,
- not_detected - liczbę niewykrytych gestów.
Dla wytrenowanej przeze mnie sieci otrzymałem:
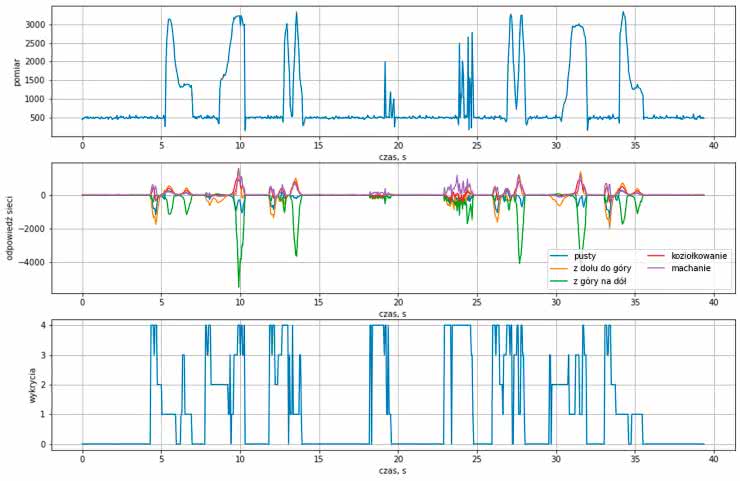
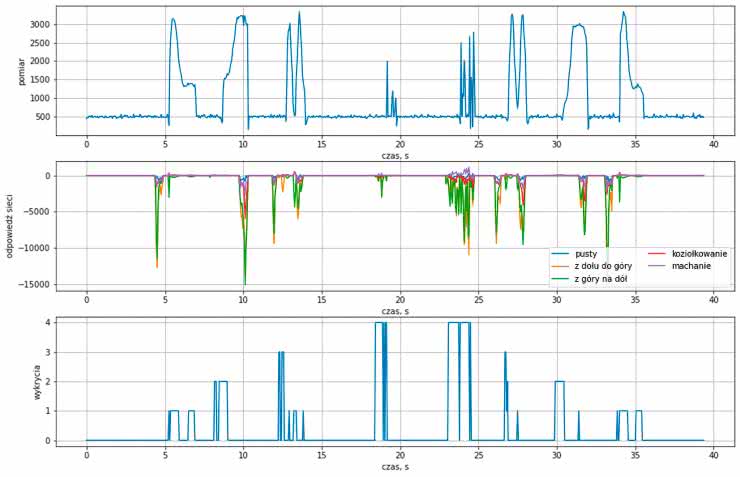
Widzimy więc, że pomimo wykrycia wszystkich symboli otrzymaliśmy także dużo błędnych wartości. Jeszcze więcej informacji uzyskamy z rysunku 9. Pierwszy wykres to nasz testowy przebieg, drugi to wartości zwracane w danej chwili przez każde z pięciu wyjść naszej sieci odpowiadających pustemu przebiegowi albo gestom. Ostatni wykres informuje nas, który stan otrzymał najwyższy wynik. Gdy się mu przyglądniemy, zobaczymy, że sieć poprawnie wykrywa środek gestu oraz przerwy między nimi. Kompletnie nie radzi sobie natomiast ze stanami przejściowymi! Powód jest dość prosty, w naszym zbiorze nie mamy takich przykładów. Sieć więc nie spotkała się z nimi w czasie nauki. Dlatego nie może sobie poradzić z nimi podczas pracy na zebranych danych.
Poprawiamy zbiór uczący
Przygotujemy więc zbiór uczący zawierający więcej przypadków. Nie potrzebujemy nawet zbierać nowych danych. Po prostu niewykorzystane ciągi występujące pomiędzy symbolami oznaczymy jako reprezentujące symbol pusty. Kod generujący nasz nowy zestaw pokazuje listing 3. W pierwszej pętli tak jak poprzednio wszystkie podciągi z sygnał z „ciszą” dodajemy do zbioru. Zmiana następuje w drugiej pętli. Do zbioru dodajemy wszystkie podciągi z danych z symbolami. Odpowiednią etykietę wybieramy, sprawdzając czy dany ciąg należy do któregoś z symboli. Jeżeli nie, oznaczamy go jako pusty. Tak jak poprzednio co 10. przypadek trafia do zbioru walidacyjnego, a reszta zostaje w zbiorze treningowym.
data_t = []
label_t = []
data_v = []
label_v = []
for i in range(len(d[0])-N):
d_tmp = d[0][i:i+N]
l_tmp = 0
if i % 10 != 0:
data_t.append(d_tmp)
label_t.append(l_tmp)
else:
data_v.append(d_tmp)
label_v.append(l_tmp)
for i in range(len(s)):
for j in range(len(d[i+1])-N):
d_tmp = d[i+1][j:j+N]
l_tmp = 0
for k in range(len(s[i])):
if j >= s[i][k]-K and j <= s[i][k]+K:
l_tmp = i+1
if j % 10 != 0:
data_t.append(d_tmp)
label_t.append(l_tmp)
else:
data_v.append(d_tmp)
label_v.append(l_tmp)
len(data_t), len(label_t), len(data_v), len(label_v)
Uzyskany zbiór danych prezentuje rysunek 10. Przykłady dla gestów są takie same jak poprzednio. Zmiana nastąpiła jednak dla stanu pustego. Widzimy, że obecny zbiór jest dużo bogatszy. Tym razem pokrywa on stany przejściowe, z którymi nasz model miał problemy.
Trenujemy sieć
Po uruchomieniu treningu dla sieci z 64 neuronami w warstwie ukrytej (czyli tylu, ile w pierwszym eksperymencie) uzyskujemy znacznie gorsze dopasowania. Na danych treningowych strata wynosi 0,24, a dokładność 89%. Dla zbioru walidacyjnego wyniki są gorsze. Strata wynosi 2,06, a dokładność spadła do 87%. Ten sposób sprawdzania nie jest dla nas jednak najlepszy. „Pusty” stan przejściowy różni się w końcu od symbolu jedynie o dwie skrajne próbki. Nas bardziej niż dokładność uzyskana na próbkach interesuje, czy wszystkie gesty zostaną wykryte oraz czy nie będziemy mieli błędnych detekcji.
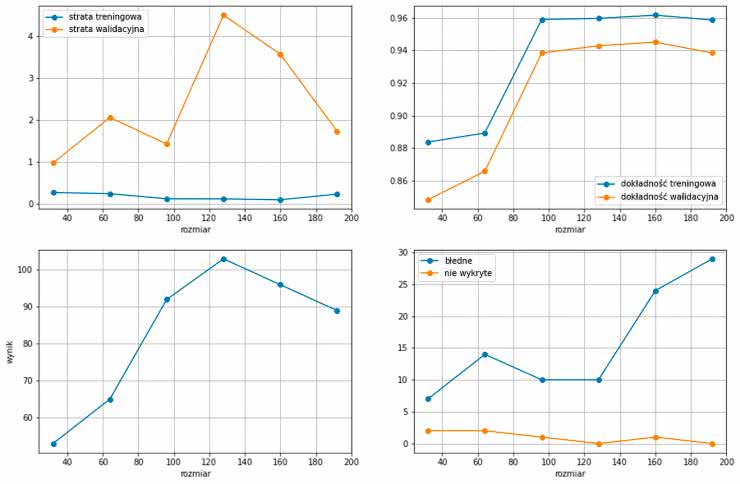
Trenujemy więc modele dla różnego rozmiaru warstwy ukrytej: od 32 do 192 neuronów, a następnie sprawdzimy ich działanie na zebranym wcześniej przebiegu. Uzyskane wyniki prezentuje rysunek 11.
Przy uruchomieniu skryptu we własnym zakresie musimy pamiętać, że inicjalizacja wag oraz sam proces trenowania sieci nie są deterministyczne, a uzyskane wyniki będą się różnić od zaprezentowanych. Górne wykresy porównują stratę oraz dokładność modeli dla danych treningowych oraz walidacyjnych.
Dolne wykresy obrazują wyniki uzyskane w teście na zebranym ciągu 8 symboli. Do pracy w sprzęcie wybrałem model z warstwą ukrytą o rozmiarze 128, ponieważ uzyskał on najwyższy wynik oraz wykrył wszystkie symbole. Odpowiedzi wybranego modelu w czasie prezentuje rysunek 12 (wykresy dla pozostałych modeli znajdują się w notatniku [3]). Widzimy, że znacznie lepiej radzi on sobie dla stanów przejściowych niż nasza poprzednia sieć. Jednak nadal na skraju dostajemy czasami błędne wykrycia. Jest ich jednak znacznie mniej. W mikrokontrolerze poradzimy sobie z nimi, dodając filtr. Przyjmiemy, że aby wykrycie zostało uznane, stan sieci musi być stabilny przez kilka iteracji.
Na końcu eksportujemy wybrany model do formatu tflite, który zaimportujemy do STM32CubeIde:
converter = tf.lite.TFLiteConverter.from_keras_model(model_128)
tflite_model = converter.convert()
open(‘gesture_recognition_128_v2.tflite’, ‘wb’).write(tflite_model)
Sieć w sprzęcie
Gdy mamy już wytrenowany model, przystępujemy do uruchomienia go w sprzęcie. Informację o wykrytym geście pokażemy na diodach LED. Sposób ich podłączenia prezentuje rysunek 13, a złożony model widzimy na fotografii tytułowej.
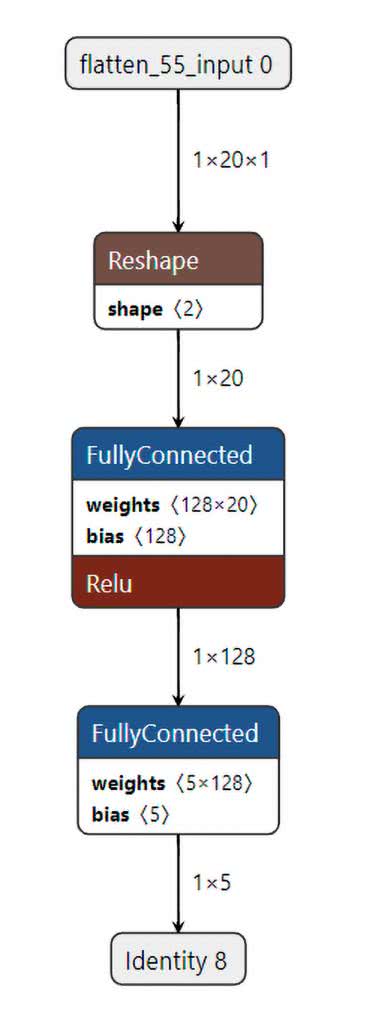
Program dla mikrokontrolera został przygotowany w STM32CubeIDE. Projekt znajdziemy w repozytorium [4]. Konfiguracja jest bardzo podobna jak dla projektu do zbierania danych. Dochodzi nam konfiguracja wyjść sterujących diodami LED oraz obsługa sieci neuronowej z biblioteki X-CUBE-AI. Zastosowana została jej wersja 7.3.0. Dodawanie sieci jest analogiczne jak w poprzednich częściach, dlatego nie będę omawiał go powtórnie. Podgląd sieci, jaki możemy wyświetlić w środowisku Cube, prezentuje rysunek 14.
Przejdźmy do napisanego kodu. Wstępną konfigurację diod LED prezentuje listing 4.
uint16_t leds[] = {
GPIO_PIN_5, GPIO_PIN_4, GPIO_PIN_10, GPIO_PIN_6};
float data[N];
int last_value = 0;
int current_value = 0;
int gesture = 0;
int count = 0;
for (uint8_t i=0; i < 4; i++)
HAL_GPIO_WritePin(GPIOB, leds[i], 0);
Numer portu, który obsługuje kolejne gesty, jest zapisany w tablicy leds. Następnie w pętli wszystkie diody są gaszone. Konfiguracja przetwornika ADC jest identyczna jak przy zbieraniu danych. Listing 5 pokazuje obsługę przerwania wywoływanego, gdy dostępne są nowe wyniki pomiarów.
volatile uint32_t adc_val;
volatile uint8_t new_adc;
void HAL_ADC_ConvCpltCallback(ADC_HandleTypeDef *hadc)
{
adc_val = HAL_ADC_GetValue(&hadc1);
new_adc = 1;
}
Zapisuje ono odczytane dane w zmiennej adc_val i ustawia flagę adc_val. Flaga jest następnie sprawdzana na początku pętli głównej pokazanej na listingu 6. Gdy zostaje ustawiona, rozpoczyna się obsługa nowych danych, a flaga jest zerowana. Następnie cała zawartość tablicy data jest przesuwana, a nowa próbka jest zapisywana na jej koniec. W ten sposób tworzony jest nowy wektor wejściowy dla sieci neuronowej.
while (1)
{
/* USER CODE END WHILE */
MX_X_CUBE_AI_Process();
/* USER CODE BEGIN 3 */
while(new_adc == 0);
new_adc = 0;
printf(“%d,”, adc_val);
for (int i=1; i < N; i++)
data[i-1] = data[i];
data[N-1] = adc_val;
current_value = process_ai(data);
if (gesture == 0) {
if (current_value != 0 && current_value == last_value) {
count++;
if (count >= THRESHOLD) {
gesture = current_value;
count = 20;
HAL_GPIO_WritePin(GPIOB, leds[gesture-1], 1);
}
} else {
count = 0;
}
} else {
count--;
if (count == 0) {
HAL_GPIO_WritePin(GPIOB, leds[gesture-1], 0);
gesture = 0;
}
}
printf(“%d\r\n”, gesture);
last_value = current_value;
if(new_adc != 0)
printf(“Timing error\r\n”);
}
Tutaj drobna ciekawostka. Początkowo zrobiłem błąd i próbki zapisywałem w odwrotnej kolejności: od najnowszej do najstarszej. Projekt działał prawie poprawnie. Jedyny błąd to gest z góry na dół był wykrywany jako z dołu do góry i odwrotnie. Pozostałe dwa gesty działały poprawnie. Zanim znalazłem prawdziwą przyczynę, próbowałem kilkakrotnie na nowo przygotowywać dane uczące dla tych dwóch gestów i szkolić ponownie sieć. Jednak ciągle działanie było takie samo. Okazuje się więc, że moje ruchy ręką są całkiem symetryczne w czasie :).
Dla przygotowanego wektora jest wywołana funkcja process_ai, która wywołuje sieć neuronową i zwraca uzyskany wynik. Jej implementację znajdziemy na listingu 7. Przypisuje ona wektory do odpowiedniej struktury i wywołujemy obliczenie sieci neuronowej. Następnie sprawdza, który gest otrzymał najwyższy wynik i zwraca tę informację.
/* USER CODE BEGIN 2 */
uint8_t process_ai(float data[])
{
ai_i32 batch;
uint8_t n;
float nn_output[AI_NETWORK_OUT_1_SIZE];
ai_input->data = data;
ai_output->data = nn_output;
batch = ai_network_run(network, ai_input, ai_output);
n = 0;
for(uint8_t i = 0; i < AI_NETWORK_OUT_1_SIZE; i++)
if (nn_output[i] > nn_output[n])
n = i;
printf(“%d,%f,%f,%f,%f,%f,”, n,
nn_output[0], nn_output[1], nn_output[2],
nn_output[3], nn_output[4]);
return n;
}
/* USER CODE END 2 */
Pozostała część pętli głównej to filtr. Pracuje on w dwóch stanach. Gdy gesture jest równe 0, jesteśmy na etapie czekania na gest. Zmienna count zlicza, przez ile kolejnych cykli wykrywana przez sieć wartość jest stała. Jeżeli kolejny wynik będzie inny niż poprzedni, następuje jej wyzerowanie. Gdy wartość zwracana przez sieć jest stała przez THRESHOLD cykli, następuje wykrycie. Zmienna gesture przyjmuje numer gestu. Następuje zaświecenie odpowiadającej mu diody LED. Do zmiennej count zostanie przypisana liczby cykli, przez które będzie wyświetlana informacja, oraz nie nastąpi żadne następne wykrycie. Przyjąłem wartość 20, czyli jedną sekundę. Gdy osiągnie ona 0, nastąpi zgaszenie diody i filtr rozpocznie pracę od początku.
Na końcu sprawdzamy, czy w czasie wykonywania pojedynczego cyklu nie nastąpiło ustawienie flagi od przerwania. Oznaczałoby to, że czas obliczeń jest za długi i będziemy tracić próbki. W takim przypadku wypisywany jest komunikat na port szeregowy.
W czasie trwania cyklu następuje także logowane danych. Jest ono umieszczone w kilku miejscach, ale dla pojedynczego cyklu składa się w jedną linię zawierającą kolejne dane rozdzielone przecinkami:
- wartość z czujnika,
- gest, dla którego sieć zwróciła najwyższą wartość,
- 5 kolejnych wyjść sieci,
- wyjście z filtru.
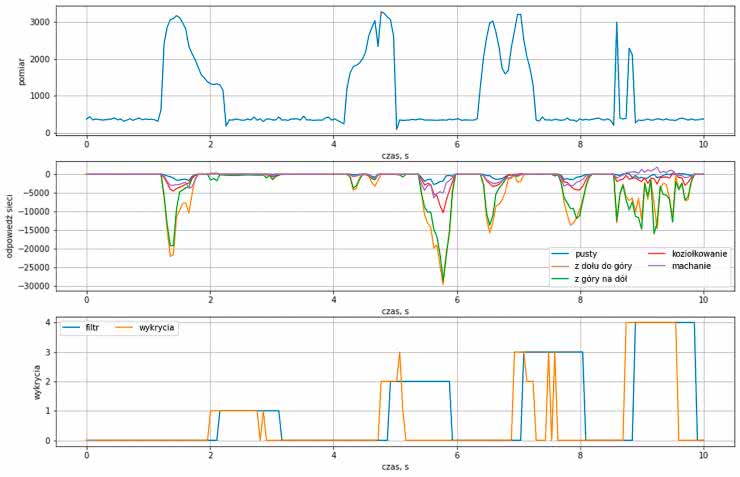
Na rysunku 15 zaprezentowane są przykładowe informacje zebrane przez mikrokontroler. Do danych zebranych przez monitor portu szeregowego zostały dodane nawiasy kwadratowe, aby uzyskać dwuwymiarową tablicę. Następnie wykresy zostały wykonane w notatniku [3]. Górny wykres to dane z czujnika.
Środkowy to wyjścia z sieci, prezentujące wartości przypisywane poszczególnym gestom. Ostatni prezentuje wyjście z sieci (kolor pomarańczowy) oraz odpowiedź naszego prostego filtru (niebieski). Uzyskany efekt możemy też zobaczyć na filmie [2].
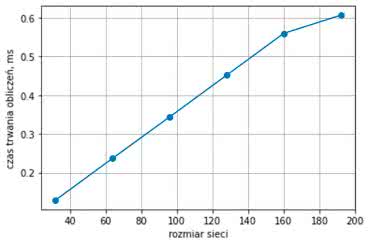
Jak pamiętamy z poprzednich odcinków, podczas konfiguracji sieci neuronowej w bibliotece możemy od razu przetestować jej działanie w docelowym sprzęcie. Sprawdziłem więc czas obliczeń dla testowanych wcześniej sieci o rozmiarach od 32 do 196. Rezultat prezentuje rysunek 16. Jak widzimy, zależność jest mniej więcej liniowa (poza siecią o rozmiarze 196). Jednak czas wykonywania jest znacznie krótszy od czasu jednego cyklu w naszym projekcie, czyli 50 ms.
Podsumowanie
Przygotowaliśmy sieć neuronową wykrywającą gesty. Przy okazji sprawdziliśmy, jaki wpływ na działanie ma zebranie reprezentatywnych danych szkoleniowych. Przygotowaliśmy także dodatkowe testy walidacyjne, które pozwoliły nam oceniać działanie sieci.
Pokazany model zawiera wiele hiperparametrów, począwszy od częstotliwości próbkowania i długości wektora, przez decyzję, jaka część symbolu musi znajdować się w badanych danych, aby uznać wykrycie, po wybór szerokości warstwy ukrytej. Dla niektórych z nich przeprowadzone zostały eksperymenty, część została wybrana obligatoryjnie. Zachęcam czytelników do wykonania własnych eksperymentów i porównań.
Rafał Kozik
rafkozik@gmail.com
Bibliografia:

 Zaloguj
Zaloguj