Układ elektroniczny
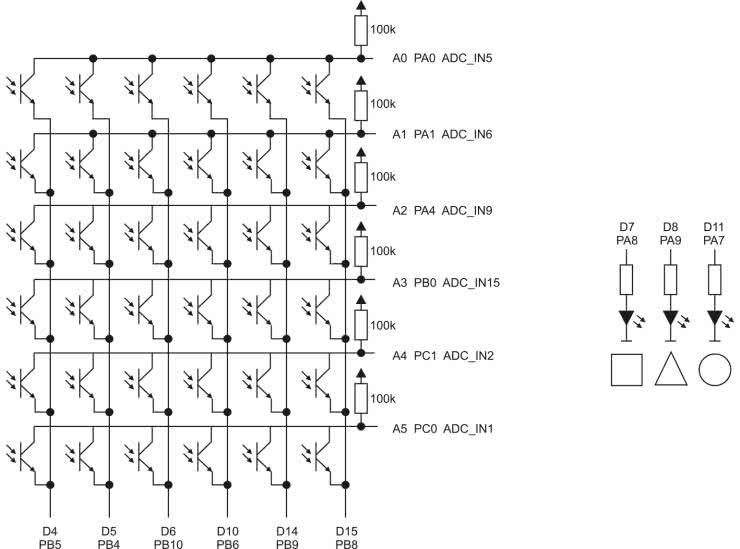
Czujnikiem, którym się posłużymy, będzie matryca trzydziestu sześciu fototranzystorów. Jej schemat wraz z połączeniami do płytki Nucleo L476RG prezentuje rysunek 1. Wszystkie kolektory fototranzystorów z pojedynczego wiersza są podłączone do wejścia przetwornika analogowo-cyfrowego oraz podciągnięte do 3,3 V za pomocą rezystora o rezystancji 100 kΩ. Emitery są połączone w kolumnach. Każda z nich jest podłączona do pinu mikrokontrolera pracującego jako wyjście. Kolumna jest aktywna, gdy na wyjściu panuje stan niski.
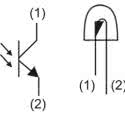
Do płytki zostały także podłączone trzy diody LED, które służą do pokazania jaki kształt został wykryty. Rysunek 2 pokazuje opis wyjść fototranzystora. Matryca została zlutowana na uniwersalnej płytce PCB. Gotowy model prezentuje fotografia tytułowa
Zbieramy dane
Zanim przystąpimy do trenowania sieci musimy zebrać dane. W repozytorium [1] znajdziemy program, który w pętli odczytuje stan fototranzystorów i wysyła je poprzez port szeregowy jako tablicę liczb w formacie JSON. Potrzebne są nam jeszcze kształty, które będziemy rozpoznawać. Ja zdecydowałem się na kwadrat o boku 4 cm, koło o średnicy 4 cm oraz trójkąt równoboczny o boku 4 cm. Kształty zostały wycięte z grubego kartonu tak, jak pokazano na fotografii 1.
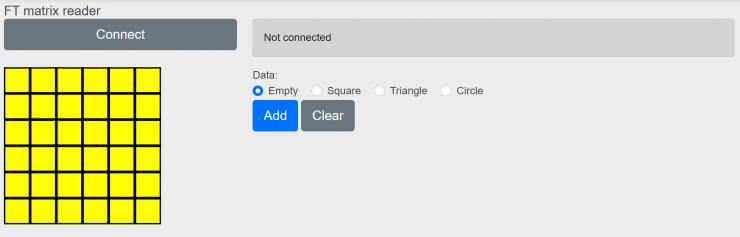
Do odczytu danych została przygotowana aplikacja w formie strony WWW, której wygląd pokazuje rysunek 3.
Znajdziemy ją w repozytorium [1] w folderze gui oraz pod adresem [2]. Jej działanie zostało sprawdzone w przeglądarce Chrome. Po jej uruchomieniu klikamy przycisk Connect i z listy wybieramy port COM naszego projektu. Gdy port zostanie prawidłowo otwarty, zostanie pokazany aktualny stan czujników. Aby zapisać przykład szkoleniowy wybieramy odpowiednią etykietę: Pusty, Kwadrat, Koło, albo Trójkąt i klikamy Add. Struktura danych z oznaczonymi przykładami będzie pojawiać się na dole strony. Jest to słownik przechowujący dwie tablice: labels zawiera etykiety, a data odpowiadające im stany matrycy.
Ja do szkolenia przygotowałem po 50 przykładów dla każdej kategorii. Wbrew pozorom pusta matryca też jest osobnym przypadkiem, który chcemy wykryć. Bez niego sieć próbowałaby zawsze dopasować którąś z pozostałych trzech możliwości. Postarajmy się, aby były one jak najbardziej różnorodne. Chcemy uwzględnić położenie figury w różnych częściach matrycy i pod różnym kątem (fotografia 2).
Jeżeli chcemy aby sieć pracowała dobrze przy różnych natężeniach oświetlenia, także powinniśmy to uwzględnić w danych uczących.
Należy także uważać, aby w czasie zapisywania przykładów nie zasłaniać matrycy ręką. Strukturę z danymi kopiujemy i tymczasowo zapisujemy w pliku tekstowym.
Trenujemy sieć
Szkicownik z kodem użytym do trenowania sieci znajdziemy w [3]. Na początku przypisujemy zebrane dane do zmiennej data. Jeżeli nie chcemy wklejać danych bezpośrednio do kodu możemy stworzyć osobny plik .py i dołączyć go do projektu. Ja jednak pozostałem przy pierwszej opcji. Aby przekonać się, co zawierają nasze dane wyrysujemy kilka przykładów za pomocą kodu z listingu 1.
fig = plt.figure(figsize=(10, 40))
n = [0, 71, 121, 171]
for i in range(4):
fig.add_subplot(1, 4, i+1)
plt.imshow(data[“data”][n[i]],
vmin=0, vmax=255, cmap=matplotlib.cm.hot)
plt.grid(False)
plt.axis(‘off’)
plt.title(data[“labels”][n[i]])
plt.show()
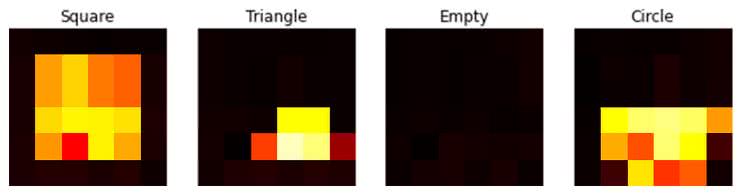
Do zmiennej n przypisujemy numery elementów z tablicy, które chcemy zobaczyć. Ja wybrałem je tak, aby pokazać po jednym obiekcie każdego rodzaju. Przykładowy wynik widzimy na rysunku 4.
Przetwornik analogowo-cyfrowy zwróci nam wyniki z przedziału od 0 do 255. Skalujemy je, aby do treningu użyć wartości zmiennoprzecinkowych z zakresu od 0 do 1. Następnie dzielimy nasze dane na dwa zbiory: większy treningowy oraz mniejszy testowy. Pierwszy zostanie użyty do nauki, a drugi do oceny uzyskanej sieci.
Struktura sieci jest pokazana na listingu 2.
model = tf.keras.models.Sequential([
tf.keras.layers.Flatten(input_shape=(6, 6)),
tf.keras.layers.Dense(64, activation=’relu’), #64
tf.keras.layers.Dropout(0.2),
tf.keras.layers.Dense(4)
])
model.fit(x_train, y_train, epochs=400)
model.evaluate(np.array(x_test), np.array(y_test), verbose=2)
1/1 - 0s - loss: 0.0960 - accuracy: 0.9500 - 19ms/epoch - 19ms/step
[0.09596162289381027, 0.949999988079071]
Wejściem jest wektor długości 36: po jednej liczbie z każdego czujnika. Następnie mamy warstwę ukrytą złożoną z 64 neuronów z funkcją aktywacją ReLU. Warstwa wyjściowa składa się z 4 neuronów, odpowiadających czterem możliwym stanom: pusty, kwadrat, trójkąt i koło. Wykonanych zostało 400 iteracji algorytmu szkolenia:
Na końcu sprawdzamy uzyskane dopasowanie na zbiorze testowym:
Ja uzyskałem wynik:
1/1 - 0s - loss: 0.0960 - accuracy: 0.9500 - 19ms/epoch - 19ms/step[0.09596162289381027, 0.949999988079071]
Warto przeprowadzić eksperymenty dla innej konfiguracji sieci oraz czasu szkolenia. Możemy także trochę podejrzeć na jakie kształty reagują poszczególne neurony wyrysowując wagi dla każdego z neuronów warstwy pośredniczącej. W przybliżeniu odpowiadają one kształtowy na jaki czuły jest poszczególny neuron. Warstwa wyjściowa otrzymuje wyniki tych częściowych dopasowań i na ich podstawie “podejmuje decyzję”.
Ostatni element kodu odpowiada za konwersję modelu to TFLite i zapisaniu go do pliku: analogicznie jak w przykładzie z funkcją XOR.
Mikrokontroler
Projekt dla mikrokontrolera tworzymy w środowisku CubeMX analogiczne jak w pierwszym eksperymencie. Tym razem konfiguracja jest bardziej rozbudowana, gdyż obejmuje też przetwornik analogowo cyfrowy. Znajdziemy ją w repozytorium [4].
W pętli głównej najpierw wykonujemy odczyt wartości z kolejnych fototranzystorów, skalujemy je dzieląc przez 255.0f i zapisujemy w dwuwymiarowej tablicy float. Następnie wywołujemy funkcję n = MX_X_CUBE_AI_Process(a). Zwraca ona liczbę odpowiadającą wykrytemu kształtowi, na podstawie której zaświecona zostaje odpowiednia dioda. Samą implementację wywołanej funkcji znajdziemy w pliku X-CUBE-AI/App/app_x-cube-ai.c oraz na listingu 3.
uint8_t MX_X_CUBE_AI_Process(float a[6][6]){
/* USER CODE BEGIN 6 */
ai_i32 batch;
uint8_t n;
float max;
float nn_output[AI_TF_MATRIX_OUT_1_SIZE];
ai_input->data = a;
ai_output->data = nn_output;
batch = ai_tf_matrix_run(tf_matrix, ai_input, ai_output);
n = 0;
for(uint8_t i=1; i < 4; i++) {
if (nn_output[i] > nn_output[n]) {
n = i;
}
}
printf("%d, %f, %f, %f, %f\r\n", n, nn_output[0],
nn_output[1], nn_output[2], nn_output[3]);
return n;
/* USER CODE END 6 */
}
Najpierw wypełniamy struktury ai_input i ai_output wskaźnikami do zmiennych przechowujących dane. Następnie wywołujemy funkcję ai_tf_matrix_run, która przeprowadza obliczenia sieci neuronowej. Na końcu musimy jeszcze znaleźć, dla którego wyjścia została zwrócona najwyższa wartość. W ten sposób rozstrzygamy jaki kształt został wykryty. Informacja ta zostanie zwrócona do pętli głównej. Dodatkowo na port szeregowy są wysyłane wszystkie informacje. Po zaprogramowaniu mikrokontrolera możemy przetestować działanie sieci neuronowej na danych zbieranych z czujników na żywo. Działanie gotowego układu pokazuje film [5].
Podsumowanie
W artykule zostały pokazane kolejne etapy, które są charakterystyczne dla implementacji sieci neuronowych:
- zbieranie danych,
- trening sieci,
- testowanie gotowej sieci.
Najtrudniejszy i najbardziej pracochłonny jest pierwszy z nich. Aby zapewnić prawidłowe działanie musimy dostarczyć dane podobne do tych, z którymi sieć spotka się w swoje pracy. W naszym przypadku będzie to zwrócenie uwagi na różne położenie kształtów oraz różne warunki oświetlenia. Mam nadzieje, że ten projekt będzie inspiracją dla czytelników do używania sieci w własnych rozwiązaniach dla różnych rodzajów danych wejściowych.
Rafał Kozik
rafkozik@gmail.com
Bibliografia:

 Zaloguj
Zaloguj