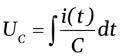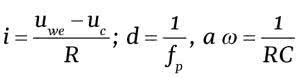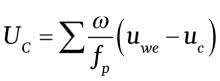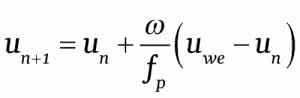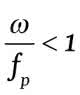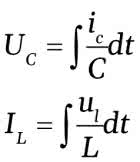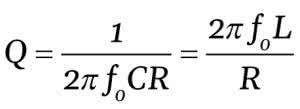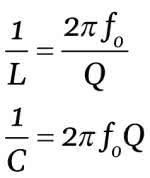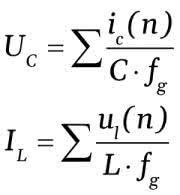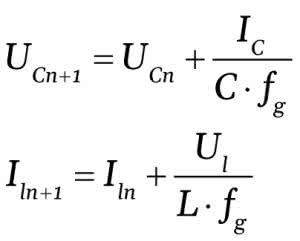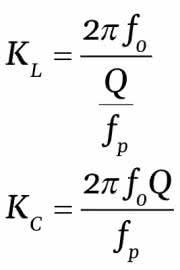Cyfrowe przetwarzanie sygnałów w praktycznych zastosowaniach (1)

Środa, 01 Marzec 2023

Przetwarzanie sygnału analogowego przez układy cyfrowe, takie jak mikrokontrolery czy układy FPGA d, w pierwszej kolejności wymaga zamiany tego sygnału na postać cyfrową. Służą do tego przetworniki analogowo-cyfrowe ADC (Analog to Digital Converter). Jeśli mamy do czynienia z sygnałem akustycznym, konieczne jest ponowne przekształcenie wartości cyfrowej (liczbowej) na postać analogową. Do tego z kolei stosuje się przetwornik cyfrowo-analogowy DAC (Digital to Analog Converter). W artykule wyjaśnimy najważniejsze zagadnienia związane z przetwarzaniem sygnałów oraz zaprezentujemy programowe implementacje kluczowych funkcji.

Dyskretyzacja sygnałów analogowych

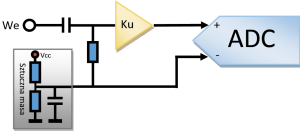
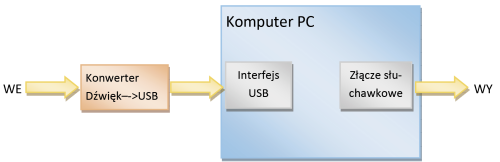
Ogólny schemat cyfrowego przetwarzania sygnału analogowego został pokazany na rysunku 1.

Rysunek 1. Ogólny schemat przetwarzania cyfrowego sygnału analogowego

Najważniejszymi parametrami przetworników ADC/DAC są:

rozdzielczość (liczba bitów),
maksymalna częstotliwość pracy.

Zamiana sygnału analogowego w znacznym uproszczeniu polega na zamianie jego wartości chwilowej na odpowiadającą jej wartość cyfrową. Jednak proces ten nigdy nie będzie przebiegał całkowicie „płynnie”. Przedział, w którym odbywa się konwersja, jest dzielony na wiele części - ich liczba zależy od rozdzielczości bitowej przetwornika (liczby bitów) jest wyrażana wzorem:

Dla przykładu, przetwornik 16-bitowy oferuje 65536 przedziałów.

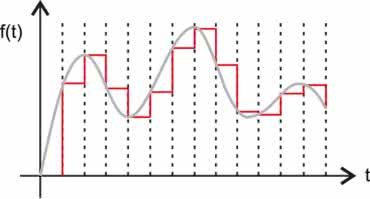
Sygnał wejściowy jest także dzielony na przedziały w dziedzinie czasu (rysunek 2).

Rysunek 2. Rysunek obrazujący dyskretyzację w dziedzinie czasu i amplitudy

Długość takiego czasu (krok próbkowania) jest odwrotnością częstotliwości próbkowania, czyli częstotliwości, z jaką pracuje nasz przetwornik ADC. Jeśli stosujemy przetwornik do sygnałów zmiennych to częstotliwość próbkowania powinna być dwa razy większa od maksymalnej częstotliwości sygnału. Jednak dla uzyskania lepszych rezultatów działania bardziej złożonych algorytmów DSP należy użyć jeszcze wyższej częstotliwości próbkowania. Dla sygnału akustycznego często stosuje się następujące częstotliwości próbkowania:

44,1 kHz,
48 kHz,
96 kHz,
192 kHz.

Podstawowe sposoby tworzenia algorytmów cyfrowego przetwarzania sygnałów

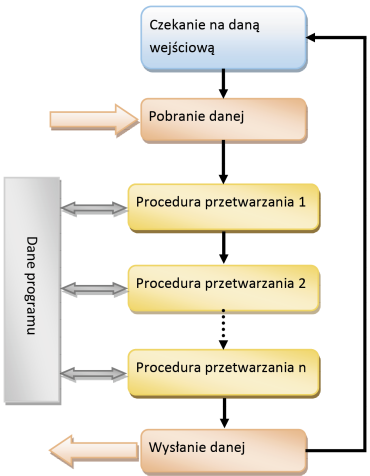
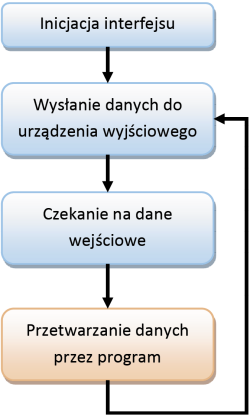
Algorytm przetwarzania sygnałów polega na cyklicznym wywoływaniu procedur (procedury), które zawierają już właściwy algorytm służący do obróbki sygnału dla naszej aplikacji. Ogólny schemat działania takiego rozwiązania pokazany jest na rysunku 3.

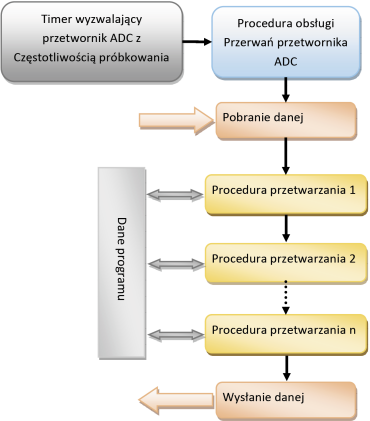
Rysunek 3. Ogólny schemat działania algorytmu przetwarzania sygnału

Procedura działa w zamkniętej pętli. Aby umożliwić działanie pozostałej części programu, można ją umieścić w oddzielnym wątku, w przypadku gdy dysponujemy systemem operacyjnym zapewniającym pracę wielowątkową. Jeśli aplikacja jest pisana dla mikrokontrolera, procedury DSP, możemy umieścić w procedurze przerwania timera lub przetwornika ADC.

Zazwyczaj najlepiej ustawić najwyższy priorytet takiego przerwania lub wątku (w przypadku programu wielowątkowego).

Realizacja DSP przy użyciu mikrokontrolera

Do niedawna podstawowymi układami do przetwarzania sygnału były specjalne procesory DSP. Jednak stopniowo są wypierane przez nowoczesne uniwersalne mikrokontrolery, które mają wysoką wydajność (częstotliwość taktowania sięgająca 1 GHz) oraz sprzętowe bloki dla arytmetyki zmiennoprzecinkowej. Układy te zazwyczaj mają też wbudowane przetworniki ADC i DAC. W tabeli 1 znajduje się kilka przykładów takich mikrokontrolerów.

Obwody wejściowe sterujące przetwornikami ADC

Przetworniki analogowo-cyfrowe, w które są wyposażone mikrokontrolery, zazwyczaj mogą pracować w dwóch trybach: różnicowym (differential) i bezwzględnym (single-ended). Tryb różnicowy polega na tym, że sygnał wejściowy podawany jest na dwa wejścia. Następnie napięcia na tych wejściach są odejmowane i dopiero wtedy odbywa się konwersja na postać cyfrową. Tryb ten powinno się stosować wtedy, gdy zależy nam na dużej precyzji pomiarów lub w przypadku gdy chcemy uzyskać dużą odporność na zakłócenia.

Mikrokontroler w czasie normalnej pracy wytwarza szerokie spektrum zakłóceń zarówno elektromagnetycznych, jak i spadków napięć tworzących się na masie układu elektronicznego. Co prawda zazwyczaj masa stopnia analogowego jest doprowadzona do innych wyprowadzeń układu scalonego niż masa cyfrowa, jednak nie da się całkowicie wyeliminować tych zakłóceń. Praca w trybie różnicowym powoduje, że zakłócenia te wpływają w tym samym stopniu na obydwa wejścia przetwornika i wzajemnie się kompensują.

Rysunek 4. Schemat działania algorytmu DSP dla mikrokontrolera, gdzie procedura przetwarzania sygnału wyzwalana jest timerem i jest wykonywana jako obsługa przerwania dla przetwornika ADC

Taka konfiguracja wejść przetwornika ADC z powodu jej wyżej opisanych zalet jest bardzo korzystna do stosowania w układach do przetwarzania dźwięku. Dodatkową zaletą jest to, że jeżeli na wejście przetwornika ADC podamy sygnał różnicowy, to po konwersji otrzymujemy przebieg zmienny i nie musimy usuwać składowej stałej.

W układach, w których dokonujemy dokładnego pomiaru napięć, które mogą przyjmować dodatnie lub ujemne wartości, również warto stosować tryb różnicowy. W układzie tym łatwiej ustalić punkt zerowego napięcia i nie jest on zależny od czułości przetwornika, która tylko w przybliżeniu jest równa wartości katalogowej oraz może się zmieniać pod wpływem temperatury.

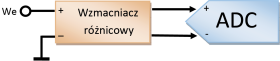
Rysunek 5. Obwód wejściowy przetwornika ADC ze wzmacniaczem różnicowym

Obwód wejściowy układu przetwarzania sygnału może być skonstruowany jako wzmacniacz różnicowy lub zwykły wzmacniacz ze sztuczną masą. W pierwszym przypadku możemy bezpośrednio podłączyć wyjścia wzmacniacza do wejść przetwornika (rysunek 5), a w przypadku obwodu ze sztuczną masą do jednego z wejść można podłączyć wyjście wzmacniacza, a do drugiego napięcie sztucznej masy (rysunek 6).

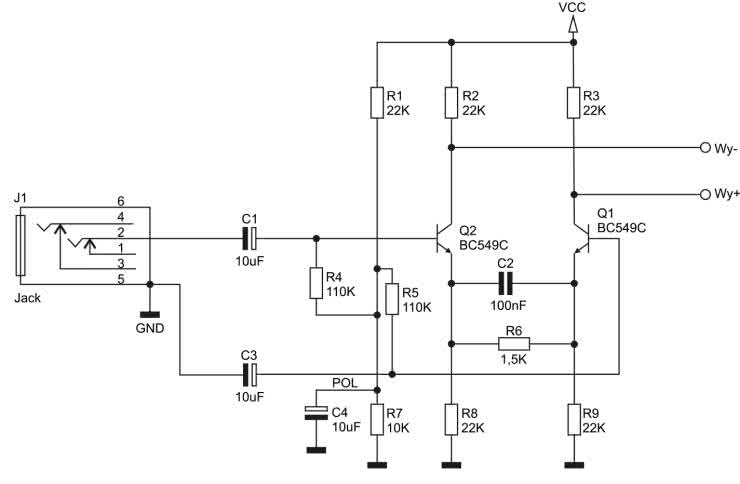
Rysunek 6. Obwód wejściowy przetwornika ADC ze sztuczną masą

Wartość napięcia wyjściowego wzmacniacza będzie podana względem sztucznej masy. Przykładowy wzmacniacz różnicowy o wzmocnieniu 10 przeznaczony dla sygnału akustycznego został pokazany na rysunku 7.

Rysunek 7. Przykładowy wzmacniacz różnicowy o wzmocnieniu 10 przeznaczony dla sygnału akustycznego

Układy z zewnętrznymi przetwornikami

Korzystanie z wewnętrznych przetworników ADC i DAC mikrokontrolera znacznie upraszcza projekt układu elektronicznego. Jednak gdy zależy nam na bardzo wysokich parametrach przetwarzania, należy zastosować oddzielny układ ADC, ponieważ większość mikrokontrolerów jest wyposażona w przetworniki o niewielkiej rozdzielczości (zazwyczaj 12, a rzadko 16 bitów).

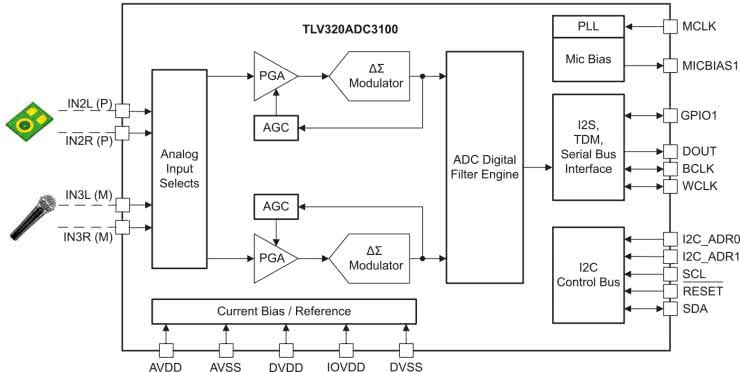
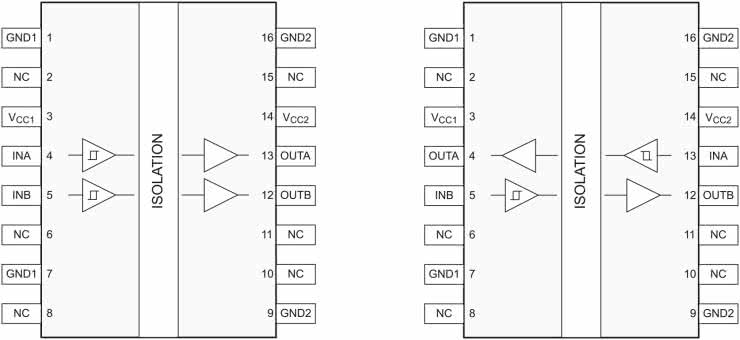
Rysunek 8. Przykładowy przetwornik dwukanałowy ADC 24-bitowy z maksymalną częstotliwością próbkowania wynoszącą 192 kHz

Najlepiej wybrać układ przetwornika ze zintegrowanym wzmacniaczem o regulowanym wzmocnieniu - schemat blokowy takiego komponentu został pokazany na rysunku 8. Układy takie zazwyczaj są sterowane poprzez magistralę szeregową (np. SPI lub I²C). Co może mieć duży wpływ na obniżenie poziomu zakłóceń. Pomiędzy torem analogowym i cyfrowym przesyłane są dane w postaci binarnej. Do przesyłania tych danych możemy użyć układów sprzęgających optycznie (transoptory) lub pojemnościowo. W zastosowaniach, w których występuje duża prędkość transmisji, raczej stosuje się pojemnościowe układy sprzęgające. Przykładowy układ tego typu pokazano na rysunku 9.

Rysunek 9. Przykładowy układ ze sprzężeniem pojemnościowym

Realizacja przetwarzania DSP na komputerze klasy PC

Najprostszym sposobem przetwarzania dźwięku jest przetwarzanie za pomocą komputera, ponieważ nie wymaga konstruowania układu elektronicznego. Jako wejścia i wyjścia dla przetwarzanego sygnału może posłużyć wbudowana karta dźwiękowa lub dołączana przystawka, która komunikuje się z komputerem przez złącze USB (rysunek 10).

Rysunek 10. Schemat funkcjonalny konfiguracji przetwarzania dźwięku przez komputer PC

Jeśli chcielibyśmy zaprojektować program do tworzenia efektów dźwiękowych dla gitary elektrycznej, to powinniśmy zastosować specjalny konwerter. Należy dodać, że parametry tego urządzenia są bardzo ważne dla jakości działania naszego algorytmu, a co za tym idzie jakości dźwięku wyjściowego. Dla efektów gitarowych ważnym parametrem jest poziom zakłóceń, dobrze by było również aby przystawka działała z częstotliwością przynajmniej 96 kHz. Przykład takiego urządzenia został pokazany na fotografii 1.

Fotografia 1. Przykładowa przystawka wysokiej klasy do komputera PC

Projekt DSP w systemie Windows

Jednym z dostępnych w systemie Windows interfejsów do obróbki dźwięku jest pakiet Core Audio API (rysunek 11). Daje on możliwość użycia każdego urządzenia dźwiękowego w systemie. Za jego pomocą można wybrać dowolne urządzenie i określić jego stan (np. czy jest podłączone lub czy jest aktywne) lub wybrać urządzenie domyślne. Interfejs ten bazuje na technologii COM, tak więc musimy programować przy użyciu interfejsów.

Rysunek 11. Struktura działania Core Audio API

Do naszych potrzeb wystarczą następujące interfejsy:

IMMDeviceEnumerator
IMMDevice
IAudioClient
IMMDevice
IAudioRenderClient
IAudioCaptureClient
IMMDeviceCollection
IPropertyStore

Interfejs IMMDeviceEnumerator służy do utworzenia listy wszystkich urządzeń w systemie, która jest umieszczana w obiekcie interfejsu IMMDeviceCollection lub do pobrania urządzenia domyślnego. Służą do tego funkcje pokazane na listingu 1.

Listing 1. Funkcje interfejsu IMMDeviceEnumerator

HRESULT EnumAudioEndpoints(
[in] EDataFlow dataFlow,
[in] DWORD dwStateMask,
[out] IMMDeviceCollection **ppDevices
);

HRESULT GetDefaultAudioEndpoint(
[in] EdataFlow dataFlow,
[in] ERole role,
[out] IMMDevice **ppEndpoint
);

Interfejs IMMDevice zawiera informacje o urządzeniu i za jego pomocą można tworzyć interfejsy pochodne służące do przesyłu danych do i z urządzeń dźwiękowych. Jeśli chcielibyśmy uzyskać nazwę urządzenia reprezentowanego przez obiekt IMMDevice, możemy użyć funkcji pokazanej na listingu 2.

Listing 2. Funkcja pozwalająca uzyskać nazwę urządzenia reprezentowanego przez obiekt IMMDevice

HRESULT OpenPropertyStore(
[in] DWORD stgmAccess,
[out] IPropertyStore **ppProperties
);

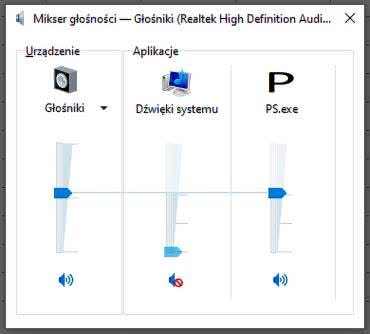
Ponadto, dla urządzenia wyjściowego tworzone jest wirtualne urządzenie, które jest widoczne w mikserze dźwięków (rysunek 12).

Rysunek 12. Wirtualne urządzenie, które jest widoczne w mikserze dźwięków systemu Windows

Interfejsy IAudioClient, IaudioRenderClient i IAudioCaptureClient służą już do sterowania samą transmisją danych. Za ich pomocą możemy określić liczbę danych w buforach, tworzyć bufory wejściowy i wejściowy oraz wysyłać i odbierać dane. Struktura takiego projektu została pokazana na rysunku 13.

Rysunek 13. Uproszczony schemat programu pokazujący działanie algorytmu przetwarzania danych

Filtr dolno- i górnoprzepustowy

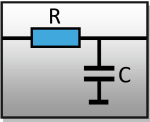
Najprostszy filtr elektroniczny RC został pokazany na rysunku 14.

Rysunek 14. Najprostszy filtr elektroniczny RC

Aby zobrazować jego działanie w dziedzinie czasu poddanego dyskretyzacji, najprościej jest zasymulować proces ładowania kondensatora, który możemy opisać wzorem:

Wytłumaczę teraz zasadę całkowania numerycznego. Wynika ona z definicji całki - całka jest to suma wszystkich wartości funkcji pomnożonych przez krok całkowania w danym przedziale. Liczba sumowań jest równa długości przedziału podzielonego przez krok całkowania, a w teoretycznym przypadku krok ten dąży do 0. Czyli według definicji sumowań jest nieskończenie wiele. W naszym przypadku możemy przyjąć, że czas dykretyzacji d (odwrotność częstotliwości próbkowania) jest bardzo mały i możemy wzór na całkę w przypadku dyskretnym (w dziedzinie liczb naturalnych) napisać tak:

Możemy to równanie zastosować w naszym przypadku. Ponieważ:

gdzie: fp - częstotliwość próbkowania.

Zatem:

Równanie to możemy zapisać w formie rekurencyjnej:

W języku „C” powyższe równanie będzie miało następującą postać:

Uc += (Uwe - Uc)*2*PI*fg/fp;

Kod ten wykonywany jest dla każdego cyklu obliczeń z częstotliwością próbkowania i daje nam symulację filtru dolnoprzepustowego pierwszego rzędu. Jeśli chcemy zwiększyć stromość charakterystyki filtru, możemy zastosować połączenie kaskadowe filtrów.

Możemy to rozwiązanie pokazać w postaci analogii do układu elektronicznego, a dzięki temu, że sygnał jest przetwarzany cyfrowo, układ ma lepsze parametry niż połączenie zwykłych obwodów RC, bowiem obwody wzajemnie się nie obciążają. Na schemacie możemy to zaprezentować, stosując bufory pomiędzy filtrami (rysunek 15). Filtr ten może być stosowany zarówno w aplikacjach do przetwarzania dźwięku, jak i w układach automatyki do redukcji zakłóceń sygnału.

Rysunek 15. Zobrazowanie filtru cyfrowego w postaci blokowej

Na tej samej zasadzie możemy zaprojektować filtr górnoprzepustowy. Wszystkie powyższe równania są adekwatne i do tego przypadku. Różnica polega tylko na wyliczeniu napięcia wyjściowego - wynosi ono:

Uwy = Uwe-Uc

Struktury filtrów

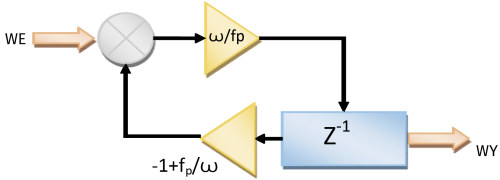
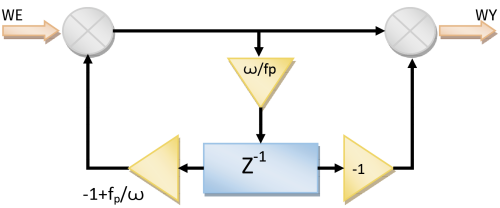
Diagram pokazujący działanie filtru dolnoprzepustowego znajduje się na rysunku 16, z kolei diagram dla filtra górnoprzepustowego znajduje się na rysunku 17.

Rysunek 16. Diagram pokazujący działanie filtru dolnoprzepustowego

Chociaż pokazana struktura filtru bazuje na transformacie w dziedzinie Z, można mimo to zinterpretować ją w bardzo prosty sposób. Symbol Z-1 reprezentuje komórkę pamięci, która jest modyfikowana przy każdym cyklu przetwarzania sygnału. Żółte trójkąty oznaczają współczynniki, przez które mnożony jest sygnał, a szare okręgi to zwykłe sumatory.

Rysunek 17. Diagram pokazujący działanie filtru górnoprzepustowego

Sposób liczenia Z-transformaty i jej własności będą opisane w dalszej części cyklu.

Listing 3. Reprezentacja filtru dolnoprzepustowego w języku C++ i przykładowa procedura składająca się z trzech filtrów połączonych kaskadowo

#define FP 96000 // Częstotliwość próbkowania
#define PI 3.141592 // stała π

class CFiltr // Klasa reprezentująca filtr
{
public:
CFiltr(double fg) : FG(fg) {} // Konstruktor
double Przetwarzanie(double we) // Procedura przetwarzania dźwięku
{
return Kondensator += (we - Kondensator) * 2 * PI * FG / FP;
}
private:
double FG; // Częstotliwość graniczna
double Kondensator = 0; // Wartość napięcia na kondensatorze
};

//implementacja 3 filtrów o częstotliwości granicznej 1000 Hz
CFiltr F1(1000), F2(1000), F3(1000);

double ProceduraPrzetwarzaniaDzwieku(double we)
{
// Kaskadowe połączenie trzech filtrów
return F3.Przetwarzanie(F2.Przetwarzanie(F1.Przetwarzanie(we)));
}

Program na listingu 3 stanowi reprezentację filtru dolnoprzepustowego w języku C++ i przykładową procedurę składającą się z trzech filtrów połączonych kaskadowo. W podobny sposób można stworzyć filtr górnoprzepustowy - listing 4.

Listing 4. Reprezentacja filtru górnoprzepustowego w języku C++

class CFiltr // Klasa reprezentująca filtr
{
public:
CFiltr(double fg) : FG(fg) {} // Konstruktor
double Przetwarzanie(double we) // Procedura przetwarzania dźwięku
{
Kondensator += (we - Kondensator) * 2 * PI * FG / FP;
return we - Kondensator;
}
private:
double FG; // Częstotliwość graniczna
double Kondensator = 0; // Wartość napięcia na kondensatorze
};

Warunek stabilności

Równanie opisanego filtru można również potraktować jako algorytm iteracyjny:

Xn+1=F(Xn)

Zbieżność takiego równania występuje tylko wtedy, jeśli pochodna funkcji jest mniejsza od 1:

F’(X)<1;

czyli w naszym przypadku:

Jest to warunek poprawnego działania filtru.

Filtr pasmowoprzepustowy

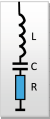
Taki filtr można zaprojektować na zasadzie działania odpowiednika układu elektronicznego (rysunek 18).

Rysunek 18. Filtr pasmowoprzepustowy jako układ RLC

Możemy dla obwodu rezonansowego RLC napisać następujące równania:

A z praw Ohma i Kirchhoffa otrzymujemy:

Uwe = Uc+Il*R+UL

Ponieważ dysponujemy dowolnym zakresem wartości wszystkich elementów, a tylko od dwóch zależą parametry obwodu rezonansowego, czyli dobroć Q i częstotliwość rezonansowa F0, możemy dla uproszczenia przyjąć R=1. Ponieważ chcemy wyznaczyć wartości C i L nie użyjemy powszechnie znanego wzoru na częstotliwość rezonansową, ale użyjemy do tego wzoru na dobroć obwodu rezonansowego:

Na podstawie tych wzorów można wyznaczyć L i C. Dla naszych obliczeń najlepiej wyznaczyć odwrotności tych wielkości:

Tak jak w poprzednim omówieniu filtrów możemy całkę zastąpić równaniem w dziedzinie liczb naturalnych:

Możemy to zaprezentować w postaci rekurencyjnej:

Czyli w języku C będziemy mieli następujące wyrażenia:

UC += IL*2*PI*F0*Q/FG
ul = UWE-IL-UC
IL += ul*2*PI*F0/Q/FG

gdzie Uwe - wartość napięcia wejściowego.

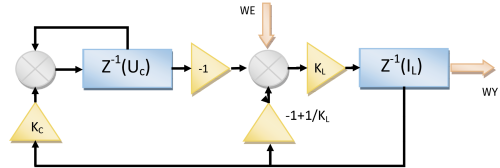
Wartością na wyjściu filtru jest napięcie na rezystorze, czyli prąd w obwodzie, który wynosi IL. Diagram pokazujący działanie filtru znajduje się na rysunku 19.

Rysunek 19. Diagram pokazujący działanie filtru pasmowoprzepustowego

Znaczenie wszystkich symboli jest takie samo jak dla poprzednich filtrów, natomiast:

Listing 5. Program reprezentujący filtr w języku C++

#define FP 96000 // Częstotliwość próbkowania
#define STALA_PI 3.141592 // stała π

class FiltrPasmowy : public Efekt
{
public:
FiltrPasmowy(double f = 1000, double q = 4) // Konstruktor
{
K_F = f;
K_Q = q;
}
double Przetwarzanie(double we) // Implementacja filtru
{
UC += IL * (double)(2 * STALA_PI / FP) * K_Q * K_F;
IL += (we - UC - IL) * (double)(2 * STALA_PI / FP) * K_F / K_Q;
return IL;
}

private:
double K_F;
double K_Q;

double UC = 0;
double IL = 0;
}

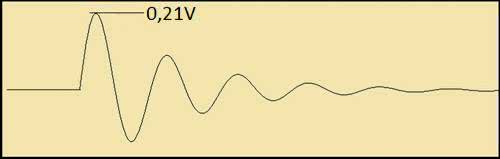
Program reprezentujący filtr został pokazany na listingu 5, natomiast jego odpowiedź impulsową na skok napięcia o wartości 1 V pokazuje rysunek 20.