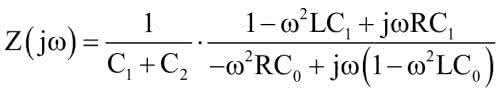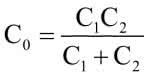Przykłady mniej lub bardziej tragicznych skutków błędów popełnianych na etapie projektu
Przyczyny wszystkich katastrof, które zostaną przytoczone w artykule, mniej lub bardziej bezpośrednio wynikały z błędu człowieka. Duża część z nich była spowodowana oprogramowaniem niezbyt dokładnie przemyślanym lub napisanym wręcz niechlujnie (nie bójmy się tego słowa). Być może katastrof tych dałoby się uniknąć, gdyby oprogramowanie było weryfikowane przez ludzi nieuczestniczących w jego pisaniu. Teraz, po fakcie, łatwo o tym mówić.
Przykładem bardzo kosztownego błędu była utrata rakiety Ariane-5. Miała to być większa i szybsza następczyni jej poprzedniczki – rakiety Ariane-4. Trwające 10 lat prace modernizacyjne obciążające budżet USA na kwotę 107 miliardów dolarów przewidywały bezpośrednie kopiowanie niektórych rozwiązań z Ariane-4. Tak się stało m.in. z feralnymi fragmentami oprogramowania. Stare oprogramowanie, choć samo w sobie nie było złe, na skutek pewnych okoliczności zgłosiło do nowego kodu błąd, który nawiasem mówiąc mógł być całkowicie zignorowany. Błąd ten został jednak poddany analizie i niestety został nieprawidłowo zinterpretowany. Spowodowało to, że moduł nawigacyjny rakiety przestał działać prawidłowo. I stało się. Kilkadziesiąt sekund po starcie rakieta rozpadła się w drobny mak. Na szczęście poza kilkoma poparzeniami nie było poważniejszych skutków – co tam 107 miliardów dolarów.
Prawdziwie tragiczny w skutkach był natomiast przypadek z uznawanymi powszechnie za bezbłędne i działające niezwykle skutecznie rakietami Patriot. Właściwie chodzi tu o cały system obrony przeciwlotniczej. Zakładał on, jak chyba wszystkie systemy tego typu, dużą mobilność baterii. Generalnie większość wyrzutni rakiet p.lot. po wystrzeleniu rakiety czym prędzej zwija się i przemieszcza w inne miejsce. W czasie operacji Pustynna Burza w Zatoce Perskiej w 1991 roku dość duży strach wzbudzały radzieckie Scudy odpalane przez Irakijczyków w kierunku baz amerykańskich. Z tego względu zdecydowano się skierować tam do obrony baterie Patriotów.
System był tak zaprojektowany, że nawet w przypadku braku podejmowania działań z rakietami powinien być zwijany, a co najmniej resetowany, maksymalnie po 8 godzinach od rozwinięcia baterii. Ponieważ operacja ta trwała „aż 90 sekund”, a w pewnym okresie konfliktu nie było żadnego zagrożenia, dowództwo podejmowało decyzję o wydłużaniu dyżurów operacyjnych nawet do 100 godzin. Lokalizacja wrogich obiektów, w tym przypadku przede wszystkim Scudów, opierała się na pomiarze czasu liczonego przez autonomiczny zegar baterii. Gdzieś jednak popełniono błąd i zegar ten nie był dość dokładny. Gdyby system był resetowany maksymalnie co 8 godzin nie byłoby żadnego problemu, ale błąd pomiaru czasu po 100 godzinach pracy bez zerowania systemu osiągał już wartość ok. 0,34 sekundy. Łatwo policzyć jaki dystans pokona w tym czasie rakieta Scud osiągająca prędkość nawet 5 macha (ok. 1500 m/s).
Wieczorem 25 lutego 1991 roku w kierunku bazy amerykańskiej Irakijczycy wystrzelili rakietę Scud. Została ona zlokalizowana przez obronę i w jej kierunku wystrzelono Patriota. Niestety, na skutek wspomnianego błędu pomiaru czasu obie rakiety minęły się w powietrzu, a Scud celnie trafił w barak z żołnierzami 475 Grupy Kwatermistrzowskiej w Dhaheranie (Arabia Saudyjska). Zginęło 28 żołnierzy, 110 trafiło do szpitala, a 150 doznało drobniejszych urazów.
Typowe przyczyny błędów projektowych
Analizując najbardziej spektakularne skutki błędów popełnianych na etapie projektów można wyróżnić kilka wyraźnych i dość często występujących przyczyn. Jednym z nich jest nieodpowiednio dobrana precyzja zmiennych. Jak wiadomo programiści dysponują szeregiem typów zmiennych, które są wybierane w zależności od zjawisk opisywanych przez te zmienne. Przykładowo, jeśli budujemy fotokomórkę zliczającą osoby wchodzące do jakiegoś pomieszczenia z pewnością nie zastosujemy danej zmiennoprzecinkowej. Nadal mamy jednak spory wybór spośród typów stałoprzecinkowych: char, byte, short integer, integer, long. Zmienne te w różny sposób obciążają zasoby komputera, w sytuacjach skrajnych istotna może być również szybkość obliczeń wykonywanych na tych typach zmiennych. Gdybyśmy do zliczania osób zastosowali licznik zmiennoprzecinkowy jest niemal pewne, że prędzej czy później wystąpiłby błąd porównywania z zerem. Czasami nie jest możliwe jednoznaczne wybranie typu zmiennej. Przykładem jest choćby arkusz kalkulacyjny. Użytkownik wpisuje liczby do poszczególnych jego komórek nie nadając im żadnego typu. Problemy z tym wystąpiły w jednej z wersji tak popularnego programu jak Excel. Okazało się, że wpisując do komórki wyrażenie =0,5–0,4–0,1 nie uzyskiwaliśmy wartości zerowej.
Innym, niestety tragicznym błędem wynikającym z nieprawidłowo dobranego typu zmiennej był przypadek z maszyną Therac-25 używanej do radioterapii. Maszyna emitowała strumień wysokoenergetycznych elektronów, którymi leczono choroby nowotworowe. Therac-25 mógł pracować w jednym z dwóch trybów różniących się energią elektronów. Ponieważ energia wiązki w silniejszym trybie była niebezpieczna dla zdrowia, a nawet życia pacjenta po uruchomieniu aparatury wykonywana była specjalna procedura testowa, która sprawdzała m.in. obecność kolimatora przysłaniającego strumień elektronów. Był to warunek konieczny do bezpiecznego uruchomienia maszyny. Procedura ta używała zmiennej 8-bitowej o wdzięcznej nazwie Class3, inkrementowanej po każdym kroku testu. Jeśli zostało stwierdzone prawidłowe położenie kolimatora zmienna Class3 była zerowana, co umożliwiało uruchomienie strumienia elektronów. Programista nie przewidział jednak, że w niewielkim procencie przypadków liczba kroków testu mogła przekroczyć 256. Oznaczało to jednak, że zmienna Class3 mogła przybrać wartość 0 nawet wtedy, gdy kolimator nie znajdował się w prawidłowym położeniu. I tak się stało. 17 stycznia 1987 pacjent poddawany leczeniu otrzymał śmiertelną dawkę. Co gorsza, operator obsługujący tego dnia maszynę otrzymywał na monitorze ostrzeżenie o nieprawidłowej sytuacji, a mimo to wymusił uruchomienie wiązki.
Czy liczba 2147483647 to dużo czy mało? Oczywiście zależy od tego, co opisuje. Organizacja IEEE czuwająca m.in. nad rozwijaniem systemów informatycznych wydała zalecenie, aby wszystkie systemy informatyczne obliczały czas korzystając z umownego punktu początkowego. Po modyfikacji wybrano ostatecznie, że ma to być 1 stycznia 1970 roku. Licznik czasu ma być inkrementowany co jedną sekundę. Twórcy systemu operacyjnego Unix, na którym jest oparty dzisiejszy MacOS zastosowali do tego celu zmienną 32-bitową.
Maksymalna liczba dodatnia, jaką można zapisać w takiej zmiennej jest równa właśnie 2147483647. Oznacza to, że 19 stycznia 2038 o godzinie 03:14:07 UTC licznik przekręci się i wrócimy do lat 70. XX wieku. Choć systemy operacyjne były wielokrotnie modyfikowane, zasada pomiaru czasu pozostaje niezmienna do dziś. Czy oznacza to katastrofę w roku 2038? Jest jeszcze trochę czasu na naprawienie błędu. Problem roku 2000 jakoś przeżyliśmy. Świat się nie skończył. Prawdopodobnie będzie tak również za 17 lat, ale warto dmuchać na zimne.
Stosowanie różnych jednostek. Jest to problem mający głębokie podłoże historyczne sięgające jeszcze epoki oświecenia i rewolucji francuskiej. Podstawowym zagadnieniem przy ustalaniu jednostek jest dobór wzorców. Bardzo często odwoływano się do różnych zjawisk fizycznych, przy czym nadal tak definiowane jednostki dla przeciętnego człowieka mogą wydawać się dziwne. Bo jeśli na przykład jeden kilogram zdefiniujemy jako masę jednego litra wody pomijając przy tym cicho inne czynniki, takie jak temperatura czy ciśnienie, to jesteśmy w stanie to sobie jakoś wyobrazić. Gorzej jest z definicją metra, gdyż uzmysłowienie sobie, że jest to odległość jaką pokonuje światło w czasie 1/299792458 sekundy jest dość trudne. Historycznym problemem jest również ambicjonalne lansowanie własnego, niestety nie metrycznego systemu przez Wielką Brytanię, której kolonialne wpływy obejmowały dużą część różnych zakątków Ziemi. Do dziś musimy zmagać się z porównywaniem cala do metra (centymetra) i funta do kilograma. O związanych z tym kłopotach przekonała się załoga Boeinga 767, który 23 lipca 1983 roku wyleciał z Montrealu do Edmonton w Kanadzie. W pewnym momencie na wysokości 12,5 kilometrów nad ziemią włączyło się ostrzeżenie o niebezpiecznie spadającym ciśnieniu paliwa. Po krótkim czasie wyłączyły się wszystkie silniki samolotu i część urządzeń zasilanych z prądnic napędzanych silnikami. W kategorii niemal cudu można uznać zakończenie tego zdarzenia. Pilot mający również doświadczenie na szybowcach zdołał wylądować na najbliższym lotnisku wojskowym. Nie było już ono wprawdzie czynne, ale jego stan ze względu na wykorzystywanie go jako tor wyścigowy był na tyle dobry, że cała przygoda zakończyła się szczęśliwie bez ofiar. Śledztwo wykazało, że przyczyną tego zdarzenia było zatankowanie zbyt małej ilości paliwa wynikające z pomylenia jednostek. Zamiast 22300 kg paliwa (co odpowiada 12700 litrów) zatankowano 22300 funtów paliwa, czyli 10115 kg. Ta zasadnicza różnica o mały włos przyczyniłaby się do tragedii.
Problemy podobnej natury mają zapewne projektanci obwodów drukowanych, na których są stosowane elementy zarówno o rastrze calowym, jak i metrycznym. Prowadząc ścieżki w rastrze calowym trzeba się nieco pogimnastykować, żeby trafić na pady elementów o rastrze metrycznym. Chociaż nowo wprowadzane elementy powinny być produkowane w rastrze metrycznym, to jednak jeszcze przez długie lata projektanci będą zmuszeniu do stosowania obu tych standardów.
Problem z własnego podwórka
Jakiś czas temu zdarzyło mi się zaprojektować urządzenie służące do rejestrowania pewnych zdarzeń. Miało ono rejestrować dane we własnej pamięci, albo przekazywać je w czasie rzeczywistym do komputera. Zarejestrowane dane były przesyłane do komputera po zakończeniu wszystkich pomiarów. Z różnych względów, w porozumieniu z użytkownikiem zdecydowano się na transmisję bezprzewodową via Bluetooth, pracujący jako przezroczysty UART. Interfejs przesyła dane z szybkością 115200 bitów na sekundę.
Do zrealizowania takiej transmisji konieczne było zastosowanie rezonatora kwarcowego o częstotliwości 11,0592 MHz. Taka częstotliwość dzielona systemowo przez 12, a następnie kolejno przez 2 daje dokładnie precyzyjny zegar taktujący transmisją o standardowej szybkości 115,2 b/s. Na rynku dostępne są jednak również kwarce 11,059 MHz. Wprowadzają one błąd zegara transmisyjnego ok. 18 ppm. Asynchroniczny interfejs radzi sobie jednak bez problemu z taką różnicą częstotliwości i transmisja przebiega bezbłędnie.
W urządzeniach były montowane w zależności od dostaw zarówno rezonatory 11,0592 MHz, jak i 11,0590.
W jednej z konfiguracji pomiarowych system składa się z kilku takich rejestratorów. Są one dodatkowo wyposażone w niezależny tor radiowy służący do zdalnego, jednoczesnego uruchamiania pomiaru przez wszystkie urządzenia pracujące na jednym obiekcie. Jest to możliwe dzięki temu, że w zestawie składającym się z kilku urządzeń tylko jedno ma status Master, reszta zaś to urządzenia podporządkowane – Slave. Operator startuje Mastera, który zanim rozpocznie rejestrację wysyła radiem synchronizacyjnym sygnał startu do pozostałych urządzeń. Jest to jeden komunikat odbierany jednocześnie przez wszystkie Slave’y. Dokładność synchronizacji jest w zupełności zadowalająca, wielokrotnie lepsza niż okres pobierania próbek. Taktowanie pobieraniem próbek jest realizowane przez indywidualny zegar w każdym rejestratorze. Jest on napędzany tym samym kwarcem, który taktuje transmisją danych. Można więc uznać, że rejestratory startują na tym samym tiku wewnętrznego zegara, przy czym tiki te mogą być przesunięte względem siebie maksymalnie o okres próbkowania. Ponieważ takie przypadki zwykle występują, więc oprogramowanie komputerowe obrabiające dane ma specjalną procedurę, która dosuwa wszystkie kanały do jednego, wspólnego punktu startowego (rysunek 1) i dalej zachowuje już oryginalne odległości między danymi.
Rejestrowane są parametry związane z czynnościami wykonywanymi przez człowieka, a właściwie zespół składający się z kilku osób. Przyjmując, że średni czas reakcji na jakiś bodziec pobudzający to około 200 ms można było przyjąć na etapie projektu, że dokładność synchronizacji na poziomie kilku, a nawet kilkunastu milisekund powinna być wystarczająca. Ale uwaga: okazało się, że istotna jest nie tylko dobra synchronizacja startu, ale też współbieżność zegarów w czasie całego pomiaru trwającego do 10 minut. Po pierwszych próbach eksploatacyjnych użytkownik stwierdził, że rozjeżdżanie się zegarów taktujących próbkowaniem nie powinno być większe niż ok. 5 ms na końcu pomiaru, czyli po 10 minutach od startu. Mogłoby się wydawać, że zastosowanie generatorów kwarcowych powinno spokojnie gwarantować spełnienie tego wymogu. Problem został pierwotnie zlekceważony. Policzmy więc.
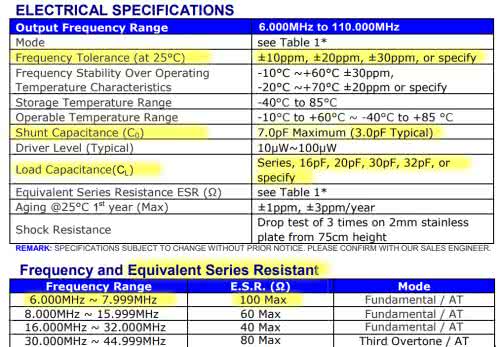
Załóżmy, że w zegarze odniesienia jest zastosowany kwarc 11,0592 MHz. Różnica częstotliwości dla zegara z kwarcem 11,0590 MHz wynosi zatem 200 Hz, co stanowi odchyłkę 18,08 ppm. Różnica pomiaru czasu na dystansie 10 minut wynikająca z zastosowania różnych rezonatorów wynosi zatem: Δt=10×60×18,08×10–6=0,006108=0,010848=10,8 ms. Nawet gdyby przyjąć, że użyto idealnych kwarców o nominalnej częstotliwości, urządzenie nie spełniałoby założeń. To pierwsze niedopatrzenie, którego można było uniknąć na etapie projektu. Ale policzmy dalej. Tym razem ograniczymy się wyłącznie do rezonatorów 11,0592 MHz. Nadal zakładamy użycie popularnych, względnie tanich rezonatorów dostępnych w internetowych sklepach wysyłkowych. Wybieramy rezonator firmy YIC. Fragment karty katalogowej został pokazany na rysunku 2.
Jak widać, jest on dostępny w wersjach z tolerancją ±10 ppm, ±20 ppm i ±30 ppm. W ofercie sklepu są jednak tylko rezonatory ±30 ppm (szkoda). I znowu, rozrzut częstotliwości ±30 ppm może spowodować odchyłkę zegarów rzędu: Δt=±10×60×30×10–6=±0,018=±18 ms, a wiec teoretycznie jeszcze gorzej niż w poprzednim rozwiązaniu. Należy jednak dodać, że wcześniej nie analizowaliśmy rozrzutu parametrów, a jedynie analizowaliśmy odchyłkę pomiaru czasu wynikającą z zastosowania kwarców o różnych wartościach znamionowych.
Jak widać, konieczne jest zupełnie inne podejście do zagadnienia. Takie, które powinno być zastosowane od początku, gdyby jasno zostały określone założenia projektowe.
Pięciomilisekundowa odchyłka pomiaru czasu po 600 sekundach oznacza, że jest ona równa 0,005/600×1000000=8,33 ppm. Prowadzi to do wniosku, że nawet kwarc ±10 ppm nie rozwiązuje problemu. Trzeba zastosować inne środki. Może to być:
- stosowanie w każdym urządzeniu dwóch niezależnych generatorów; jeden obsługiwałby interfejs komunikacyjny, drugi taktowałby próbkowaniem. Generator taktujący próbkowaniem musiałby mieć dokładność lepszą niż 8 ppm;
- stosowanie jednego generatora, który taktowałby wszystkimi rejestratorami;
- precyzyjne selekcjonowanie rezonatorów z dużej grupy tak, aby rozrzut ich częstotliwości był mniejszy od 8 ppm.
Pierwsze rozwiązanie wymagałoby dość gruntownej zmiany schematu i PCB, co raczej nie wchodzi w grę. Drugie rozwiązanie również wiązałoby się z gruntowną zmianą projektu, a sporym wyzwaniem byłaby realizacja bezprzewodowego wspólnego taktowania niezależnych urządzeń. Tę koncepcję należy również odrzucić. W zaistniałej sytuacji najbardziej sensowne wydaje się trzecie rozwiązanie. Pytanie tylko, jak selekcjonować rezonatory? Dopuszczalna różnica częstotliwości przy założeniu dokładności 8,33 ppm wynosi: Δf=11059200*8,33/1000000= 92,123136 Hz=±46,06 Hz. Do pomiaru takich różnic konieczne by było użycie częstościomierza z wyświetlaczem co najmniej 8-cyfrowym – może być problem.
Trudną sytuację ratuje nieco fakt, że nie jest wymagana bezwzględna precyzja częstotliwości, a jak najmniejszy rozrzut tego parametru. Wydaje się, że problem można rozwiązać korzystając z zestawu Analog Discovery 2. Spróbujmy.
Symulacja i pomiar rezonatorów kwarcowych z zastosowaniem programów LTspice i Analog Discovery 2
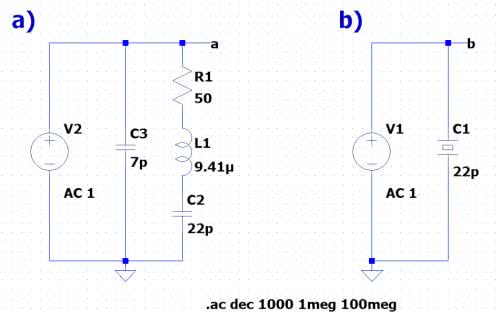
Zestaw Analog Discovery 2 zawiera m.in. narzędzie Impedance. Jak można się domyślić, służy ono do zdejmowania charakterystyk częstotliwościowych elementów biernych R, L, C lub obwodów z nich złożonych. Takim obwodem może być na przykład rezonator kwarcowy. Jego schemat zastępczy przygotowany w symulatorze LTspice pokazano na rysunku 3a. Na schemacie z rysunku 3b użyto do symulacji elementu bibliotecznego reprezentującego rezonator kwarcowy.
Jest on charakteryzowany kilkoma parametrami:
- Capacitance – odpowiednik Load capacitance z karty katalogowej rezonatora,
- Equiv. Series Resistance czyli Equivalent Series Resistance,
- Equiv. Series Inductance – indukcyjność zastępcza definiująca wraz z pojemnością capacitance podstawową częstotliwość drgań rezonatora,
- Equiv. Parallel Capacitance – odpowiednik Shunt Capacitance z noty katalogowej.
Rezonator można zatem traktować jak szeregowy obwód rezonansowy zbocznikowany pojemnością. Do katalogowej wartości tego parametru należałoby dodać jeszcze pojemność montażu.
Można spodziewać się, że charakterystyka częstotliwościowa impedancji rezonatora będzie miała minimum dla częstotliwości rezonansowej. Z pewnością byłoby tak, gdyby nie było pojemności C2. Występowałby wówczas tylko rezonans szeregowy na częstotliwości drgań rezonatora. Pojemność C2 powoduje jednak, że w obwodzie z rezonatorem wystąpi również rezonans równoległy dla częstotliwości, dla której reaktancja indukcyjności L1 zmniejszona o reaktancję pojemności C1 będzie równa co do modułu reaktancji pojemności C2. Nie jest to jednak częstotliwość pracy kwarcu. Rezonans równoległy spowoduje, że w wykresie impedancji oprócz minimum dla rezonansu szeregowego pojawi się maksimum dla rezonansu równoległego. Impedancja rezonatora o takim modelu jest równa:
gdzie:
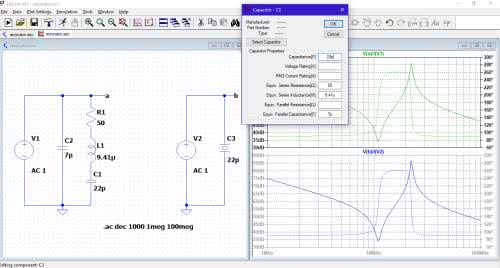
Sprawdźmy w symulatorze LTspice czy rzeczywiście zaobserwujemy dwa ekstrema wykresu impedancji. Ponieważ później będziemy chcieli sprawdzić wyniki symulacji z pomiarami rzeczywistymi, najpierw zajmiemy się rezonatorem o niższej częstotliwości niż 11,0592 MHz. Dzięki temu zminimalizujemy problemy z ewentualnym wpływem pojemnościami montażowymi, które na pewno pojawią się w rzeczywistym układzie pomiarowym wtedy, gdy nie zastosujemy specjalnego interfejsu. Rezonator symulowany ma częstotliwość drgań 6,00 MHz.
Na rysunku 4 pokazano wynik symulacji „AC Analysis”. Domyślnie obliczane jest napięcie lub natężenie prądu we wskazanej gałęzi lub elemencie. Aby uzyskać wykres impedancji konieczne jest przedefiniowanie mierzonego parametru, np. wprowadzenie wyrażenia V(a)/I(V1) pozwala obliczyć impedancję rezonatora. Jak widać wyniki uzyskane z symulatora potwierdzają rozważania o dwóch rezonansach. Pojemność Cmont symbolizuje pojemności montażowe.
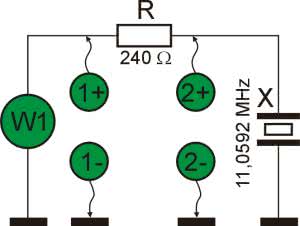
Mając tę wiedzę nie pozostaje nic innego jak zweryfikować wyniki symulacji z pomiarami praktycznymi. Uruchamiamy zatem Analog Discovery 2, a w nim narzędzie Impedance. Schemat pomiarowy przedstawiono na rysunku 5.
Rezystor R służy do pomiaru prądu płynącego w obwodzie. Prąd jest obliczany w programie na podstawie pomiaru spadku napięcia na znanej rezystancji. Napięcie na rezystorze jest równe różnicy napięć mierzonych przez 1. i 2. kanał przyrządu. Rezystor powinien być dobierany w zależności od rezystancji mierzonego elementu. Impedancja rezonatora zmienia się jednak w dość dużym zakresie, konieczny jest jakiś kompromis. Rezystor 240 Ω powinien być dobrym wyborem.
Przed pomiarem zasadniczym należy wprowadzić przyjętą rezystancję i przeprowadzić kompensację toru pomiarowego. Wcześniej określamy zakres mierzonych częstotliwości. Wprowadzamy zakres częstotliwości 5,99 MHz...6,02 MHz. Ze względu na wymaganą dużą dokładność skanowania częstotliwości wybieramy 2001 punktów (Samples=2,001k). Naciskamy przycisk ekranowy Compensation i widoczną w tabelce wartość 100 Ω zmieniamy na 240 Ω. Następnie przeprowadzamy kompensację dla obwodu rozwartego i zwartego.
Usuwamy testowany element (rezonator) z obwodu i naciskamy przycisk do open compensation. Teraz w miejsce rezonatora wkładamy zworkę i uruchamiamy kompensację do short compensation – rysunek 6. Zezwalamy na obie kompensacje naciskając przycisk Enable. Po tych czynnościach układ jest gotowy do pomiarów. Umieszczamy w obwodzie rezonator, zaznaczamy tylko opcję |Z| i uruchamiamy pomiar jednorazowy (Single). Po kilku chwilach na ekranie ukazuje się wykres impedancji rezonatora – rysunek 7. Wyraźnie widzimy dwa ekstrema charakterystyczne dla rezonansu szeregowego i równoległego, chociaż w pomiarze są one znacznie bliżej siebie niż w symulacji. Wpływają na to dość znaczne pojemności wnoszone przez kable pomiarowe.
Selekcja rezonatorów 11,0592 MHz dla rejestratora
Wracamy do zasadniczego zagadnienia, jakim jest dobór rezonatorów o najmniejszym rozrzucie częstotliwości drgań. Wiemy już, że dla uzyskania częstotliwości mieszczących się w granicach 8,33 ppm względem siebie częstotliwości drgań kwarców nie powinny różnić się o więcej niż 92 Hz.
Tym razem w narzędziu Impedance wprowadzamy zakres częstotliwości od 11,054 MHz do 11,06 MHz. Pozostawiamy 2001 punktów pomiarowych, Kompensujemy układ tak jak robiliśmy to wcześniej i przystępujemy do pomiarów. Do obwodu pomiarowego wkładamy pierwszy rezonator i uruchamiamy pojedynczy pomiar. Po chwili uzyskujemy wykres, który zapamiętujemy uruchamiając opcję +Reference → Add Trace as Reference. Wkładamy kolejny rezonator i po skończonym pomiarze ponownie zapamiętujemy jego parametry.
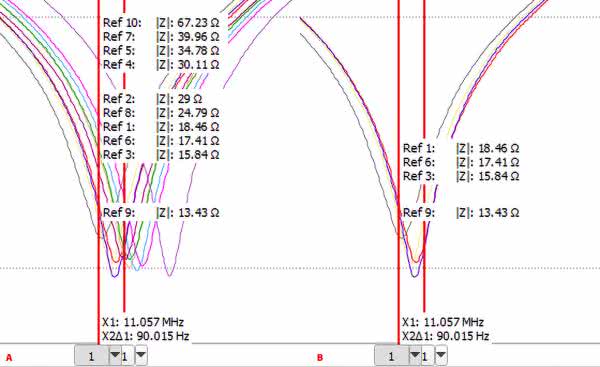
Uzyskujemy w ten sposób kolekcję wyników. Na rysunku 8 widzimy zestawienie dla 10 egzemplarzy rezonatorów 11,0592 MHz ±30 ppm. Były one kupowane jednocześnie, można więc sądzić, że pochodzą z jednej serii produkcyjnej. Zmierzony rozrzut częstotliwości rezonansowych zawiera się w zakresie 22 ppm, co odpowiada danym technicznym, ale jest wartością zbyt dużą, jak na potrzeby rejestratora. Na rysunku 8 pokazano ponadto charakterystykę rezonatora 11,059 MHz.
Na podstawie zestawienia charakterystyk można sądzić, że powinno być możliwe wyselekcjonowanie egzemplarzy, których parametry różnią się mniej niż 8,33 ppm, a więc mniej niż ok. 92 Hz. Najłatwiej taką selekcję przeprowadzić korzystając z kursorów. W tym celu umieszczamy na wykresie dwa kursory pionowe. Kursor 1. jest domyślnie kursorem referencyjnym dla 2. i pozostałych. Po rozwinięciu opcji kursora 2. można ustawić jego położenie względem kursora 1. Wybieramy oczywiście wartość 92 Hz (rysunek 9). Przesuwając teraz kursor 1. automatycznie jest przesuwany również kursor 2. Możemy więc tak naprowadzić oba kursory, aby między nimi znalazło się jak najwięcej charakterystyk. Będą one spełniały warunek rozrzutu parametrów o mniej niż 8,33 ppm.
Dla zwiększenia czytelności wyników warto wyłączyć wyświetlanie tych wykresów, które nie spełniają warunku dokładności – rysunek 10 a i b. Jeśli zachowaliśmy porządek w selekcjonowaniu rezonatorów zadanie można uznać za wykonane. Pozostaje jedynie wlutować wyselekcjonowane kwarce do rejestratorów i sprawdzić czy przeprowadzone nimi pomiary spełniają zadane warunki.
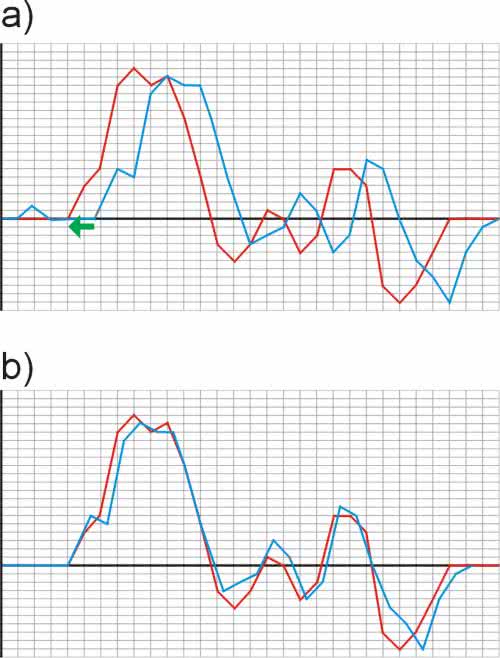
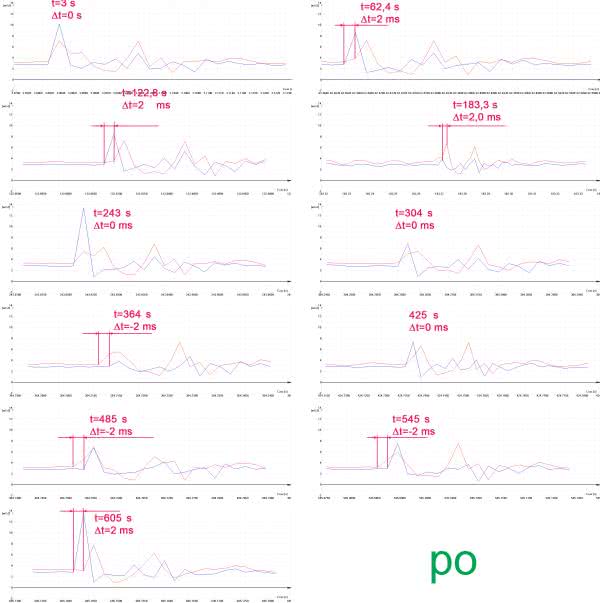
Wyniki testów zostały pokazane na rysunkach 11 i 12. Przed wlutowaniem dobranych rezonatorów przeprowadzono pomiary z rezonatorami, które pierwotnie znalazły się w rejestratorach i nie były dobierane. O tym, że problem został wcześniej całkowicie zignorowany świadczy fakt, że w jednym urządzeniu był kwarc 11,0592 MHz, a w drugim 11,059 MHz. W czasie testu rejestry były połączone ze sobą mechanicznie i rejestrowały bodźce mechaniczne pobudzające oba urządzenia jednocześnie. Po wykonaniu pomiaru trwającego nieco ponad 10 minut program komputerowy odczytał dane z urządzeń i na wszelki wypadek przeprowadził ich synchronizację polegającą na dosunięciu obu wykresów tak, aby pierwsze impulsy zaczynały się dokładnie w tej samej chwili czasowej. Sygnały były próbkowane z częstotliwością 500 Hz, a więc początkowy asynchronizm w najgorszym przypadku mógł być równy 2 ms.
Pierwszy test wykazał rozjechanie się zegarów o ok. 42 ms po 10 minutach testu. Stanowi to odchyłkę aż o 69 ppm w odniesieniu do czasu pomiaru. To wynik dyskwalifikujący dla przewidzianych zastosowań.
Drugi test już z dobranymi rezonatorami dał odchyłkę 2 ms na koniec testu trwającego również nieco ponad 10 minut. Odchyłka ta jest jednak równa odstępowi próbkowania. Parametr ten zmieniał się w czasie testu przyjmując wartości –2 ms, 0 ms i 2 ms. Można więc uznać, że poczynione działania spełniły oczekiwania sprawiające, że rejestratory mogą pracować w pomiarach synchronicznych zachowując zakładaną dokładność czasową.
Na koniec nasuwa się refleksja: czy nie jest to przypadek do złudzenia przypominający smutną historię z Patriotami?
Jarosław Doliński, EP

 Zaloguj
Zaloguj