Implementacja charakterystyk czujników w podwójnie logarytmicznym układzie współrzędnych w systemach mikroprocesorowych

Z tym kodem też tragedii nie ma, gdyż dostawcy sprzętu udostępniają często gotowe biblioteki obsługi modułów zawierających wybrane czujniki. Jeśli nawet nie, to z pewnością pomoże olbrzymia społeczność zebrana wokół danej platformy. Wynika z tego, że wystarczy pstryknąć palcami, a układ zrobi się sam. Jesteśmy już blisko takiego stanu, ale jeszcze nie dzisiaj. Poza tym jest jeszcze grupa konstruktorów, być może już na wymarciu, która lubi zrobić wszystko własnymi rękami od początku do końca.

Przystępując do konstruowania urządzenia elektronicznego, w którym mają być zastosowane różnego rodzaju sensory zwykle przeglądamy listę dostępnych na rynku elementów. Przy odrobinie szczęścia udaje się znaleźć czujniki, w których zintegrowano odpowiedni układ pomiarowy (analogowy), blok akwizycji danych i wstępnej ich obróbki oraz co najmniej jeden z popularnych interfejsów komunikacyjnych, za pośrednictwem którego dane już w postaci cyfrowej są przesyłane do systemu nadrzędnego. Zadanie konstruktora w takim przypadku ogranicza się w zasadzie do zapoznania się z rejestrami czujnika, składnią komend zapisujących i odczytujących rejestry oraz strukturą przesyłanych danych.

Same problemy

Nieco gorzej sprawa wygląda z czujnikami wyłącznie analogowymi. Konieczne jest wówczas zaprojektowanie odpowiedniego interfejsu sprzętowego oraz napisanie kodu, który dane cyfrowe uzyskane w wyniku próbkowania sygnałów analogowych z czujnika przeliczy na odpowiednią wielkość fizyczną. Typowym przykładem czujników tego rodzaju są sensory gazów. Stwarzają one problemy dwojakiego rodzaju. Po pierwsze, ich charakterystyki są bardzo, jeszcze raz powtórzę bardzo silnie nieliniowe. Po drugie, parametr wyjściowy – stężenie gazu – nie zależy wprost od bezpośrednio zmierzonego parametru czujnika, jakim najczęściej jest rezystancja. Do wyznaczenia wielkości mierzonej konieczne jest zmierzenie rezystancji czujnika w badanym środowisku (R_S) i obliczenie stosunku tej rezystancji do rezystancji czujnika w środowisku odniesienia (R_O). Same problemy. Jak zmierzyć rezystancję czujnika? Nie, o tym w tym artykule nie będzie mowy, gdyż koncentrujemy się na zupełnie innym zagadnieniu. Zakładamy, że rezystancję jakoś potrafimy zmierzyć. Obliczenie stosunku R_S/R_O z matematycznego punktu widzenie nie powinno stwarzać problemów. Pod warunkiem jednak, że znamy R_O, a mamy jedynie mgliste pojęcie o tej wielkości. Wyznaczanie R_O też nie jest tematem tego artykułu. Można jedynie powiedzieć, że R_O daje się wyznaczyć podczas kalibracji w czystej atmosferze, a co gorsze jest to parametr zmieniający się w dużym zakresie nawet w obrębie elementów jednego typu. Z tego powodu producenci zwykle nie podają w danych katalogowych konkretnej wartości R_O. Można się jedynie doszukać zakresu rozrzutu tego parametru.

Załóżmy, że jakoś przebrnęliśmy przez problemy mierzenia rezystancji i wyznaczania R_O dla konkretnego egzemplarza czujnika. Problemy na tym się nie kończą, gdyż końcową wielkość mierzoną – stężenie gazu wyrażane w jednostkach ppm (parts per milion) lub g/m³ należy obliczyć z charakterystyki czujnika udostępnianej w jego dokumentacji technicznej.

Problem zasadniczy

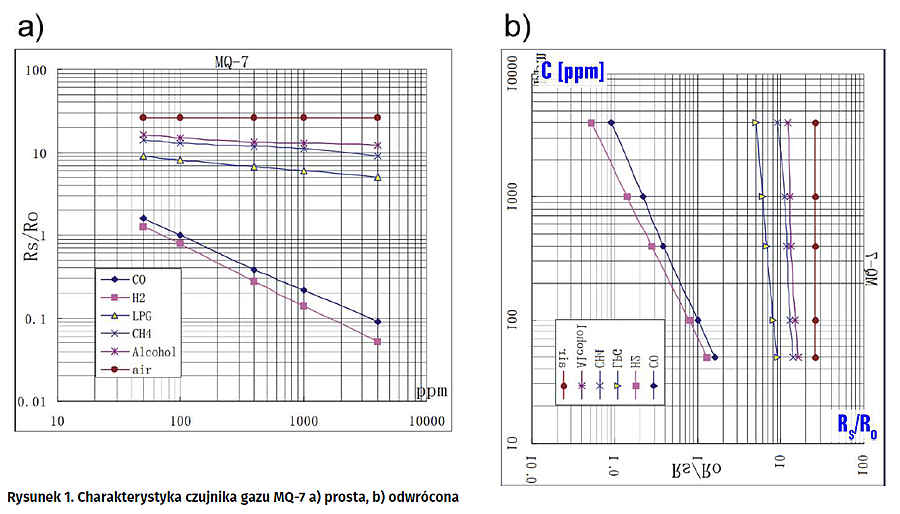
I tu ujawnia się problem zasadniczy, gdyż charakterystyki są udostępniane jedynie w postaci wykresów zamieszczanych w PDF-ach. To trochę tak, jakbyśmy je mieli tylko na papierze. Konieczne jest więc przeniesienie ich do postaci cyfrowej tak, aby można je było zaimplementować np. w programie mikrokontrolera zastosowanego w urządzeniu. Jak to zrobić? Przykładowe metody opisano niżej, wcześniej jednak jeszcze jedna istotna uwaga. Charakterystyki opisują zależność R_S/R_O w funkcji stężenia gazu (rysunek 1a), a my będziemy wykonywać operację odwrotną. W rzeczywistym układzie pomiarowym mierzony będzie stosunek R_S/R_O i na tej podstawie mikrokontroler obliczy stę?enie gazu. Oznaczmy je liter? C. Dla wygody wi?c wykres r?wnie? odwr?cimy tak, aby osie zamieni?y si? miejscami. Dalsze czynno?ci b?d? dotyczy?y wy??cznie rysunku obr?conego (żenie gazu. Oznaczmy je literą C. Dla wygody więc wykres również odwrócimy tak, aby osie zamieniły się miejscami. Dalsze czynności będą dotyczyły wyłącznie rysunku obróconego (rysunek 1b).

Metoda 1 – tablicowanie

Pierwsza metoda, to tablicowanie. Istne szaleństwo. Taka metoda może doprowadzić do zapchania całej pamięci, jeśli nie będzie jej zbyt wiele, na przykład w małych mikrokontrolerkach ATtiny. Z definicji charakterystyka tak przeniesiona będzie miała charakter dyskretny, to znaczy będzie się składała jedynie z pewnego zbioru punktów. Prawdopodobnie konieczna więc będzie interpolacja, polegająca na sztucznym wstawianiu punktów nie uwzględnionych w tablicy. Ręczne tablicowanie charakterystyki, która najczęściej jest podawana w podwójnie logarytmicznym układzie współrzędnych oznacza dodatkowe czynności przy przeliczaniu liczb.

Metoda 2 – bezpośrednie wyznaczenie formuły matematycznej

Tak nazwałem tę metodę, gdyż będzie ona polegać na wyznaczeniu wyrażenia matematycznego opisującego charakterystykę wprost z wykresu zamieszczonego w dokumentacji. Mamy tu jeden czynnik komplikujący zagadnienie i jeden ułatwiający. Komplikującym jest podwójnie logarytmiczny układ współrzędnych – obie osie (rzędnych i odciętych) mają skalę logarytmiczną. Odczytywanie danych liczbowych nie będzie więc proste. Czynnikiem ułatwiającym jest fakt, że charakterystyki podawane w takim układzie współrzędnych są w dużym stopniu liniowe. Jeśli nawet nie w całym zakresie, to można przyjąć kilka przedziałów, dla których mogą być tak traktowane.

Na rysunku 1a przedstawiono przykładową charakterystykę czujnika gazu MQ-7. Jak widać, jest on mniej lub bardziej wrażliwy na kilka rodzajów gazu. Nas będzie interesować tlenek węgla (CO). Jest to granatowa krzywa z punktami w kształcie rombów. Załóżmy, że w całym zakresie pomiarowym charakterystyka ta jest liniowa. Przymykamy oko na niewielkie odchylenie okolic punktu odpowiadającego stężeniu 400 ppm. (rysunek 2).

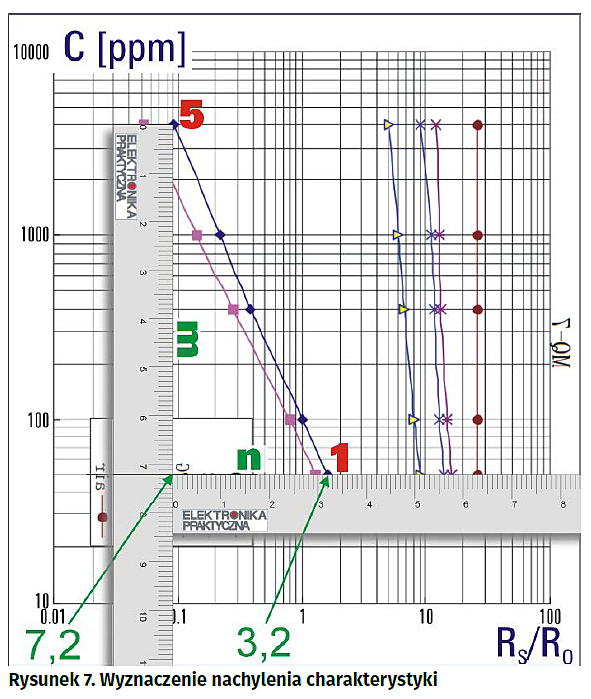
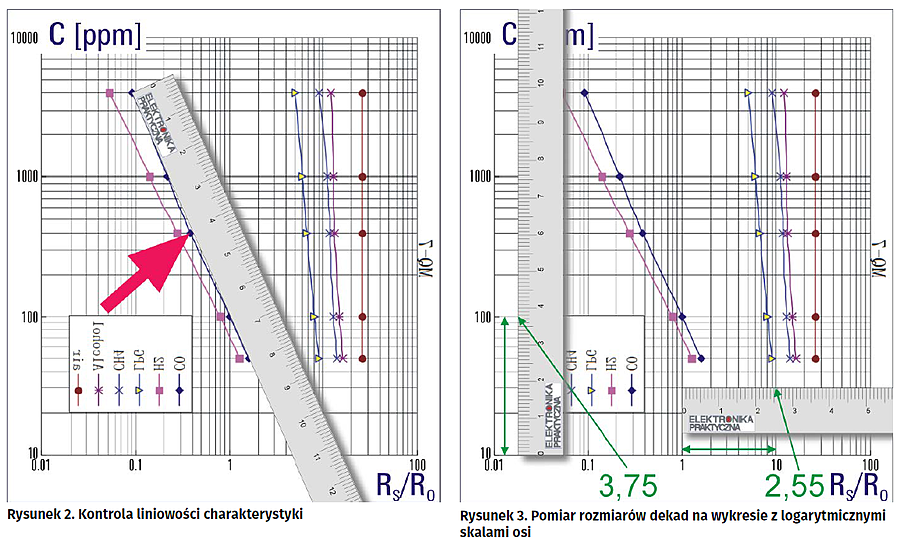
Teraz musimy nauczyć się odczytywać dane z wykresu. Chcielibyśmy robić to jak najdokładniej, mimo, że będzie to pewną niekonsekwencją wobec wcześniejszego zlekceważenia małej nieliniowości. Metoda „na oko” raczej odpada, a do pomiarów użyjemy linijki. Pierwsze co należy zrobić, to pomiar szerokości dekad na obu osiach. Wyniki będą wyrażone w centymetrach. Teoretycznie dysponując linijką z najmniejszą działką równą 1 mm powinienem podawać wyniki z taką właśnie dokładnością. Zakładam jednak, że jestem w stanie określić wynik z dokładnością do 0,5 mm. Z pomiarów przedstawionych na rysunku 3 wynika, że dekada na osi odciętych ma szerokość równą 2,55 cm, a na osi rzędnych 3,75 cm. Liczby te należy zapamiętać.

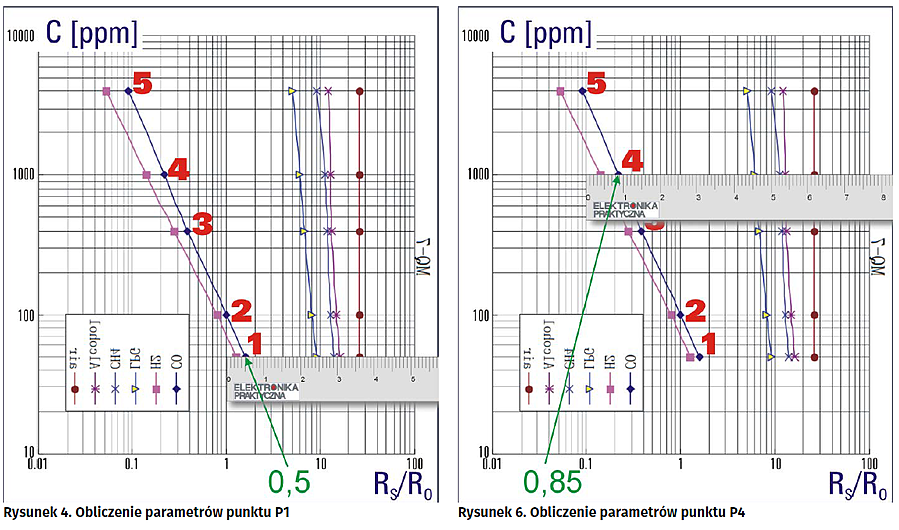
Odczytajmy teraz parametry punktu oznaczonego cyfrą „1”. Jest to punkt położony dokładnie na linii wyznaczającej stężenie 50 ppm. Odstępy między liniami w pierwszej dekadzie na osi odciętych wynoszą 10, w drugiej 100 itd. Ponieważ punkt leży dokładnie na linii nie będą potrzebne żadne przeliczenia dla tej rzędnej. Należy natomiast wyznaczyć odpowiadający temu stężeniu stosunek R_S/R_O. Mierzymy więc odległość punktu „1” od najbliższej linii rozpoczynającej dekadę, w której ten punkt leży, a więc od linii o odciętej 1. Odległość ta jest równa 0,5 cm (rysunek 4), a zatem R_S/R_O jest w tym punkcie równe (patrz - plik PDF).

Punkt „1” jest opisany jako P1(1,57, 50). Punkt „2” nie wymaga obliczeń, gdyż leży na przecięciu linii. Dane odczytujemy wprost: P2(1, 100). Dla punktu „3” postępujemy podobnie, jak w punkcie „1”. Rzędna jest równa 400, a odległość na linii odciętych od punktu 0,1 jest równa 1,5 cm (rysunek 5). Analogicznie dla punktu „4” (rysunek 6) możemy wyznaczyć wartość, ale pamiętając, że punkt leży w dekadzie 0,1 ostatecznie R_S/R_O jest równe 0,215. Zatem punkt 4 jest opisany jako: P4(0,215, 1000). Ostatni punkt „5” leży na przecięciu linii, dane wyznaczamy wprost z wykresu: P5(0,09, 4000).

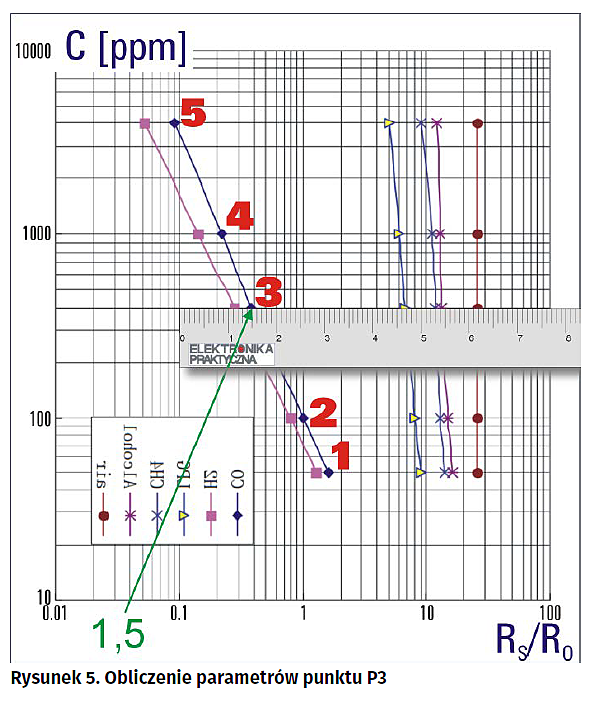
Dane punktów P1...P5 będą potrzebne w innych operacjach, a teraz już jest ten moment, w którym można wyprowadzić wyrażenie matematyczne opisujące charakterystykę czujnika dla gazu CO. Założyliśmy już, że w układzie podwójnie logarytmicznym mamy do czynienia z wykresem liniowym, dla którego w normalnym układzie obowiązywałoby znane z matematyki wyrażenie y=a*x+b. Uwzględniając skale logarytmiczne wyrażenie to przyjmuje postać: log(C)=a*log(R_S/R_O)+log(b) Współczynnik a jest równy tangensowi nachylenia charakterystyki i obliczamy go graficznie z wykresu, tak jak to przedstawiono na rysunku 7. Pamiętamy jednak o konieczności normalizowania linijkowych pomiarów parametrów m i n do szerokości dekad poszczególnych osi. Mamy więc a=m/n, gdzie zmierzone linijką parametry m i n po normalizacji są równe odpowiednio 7,2 cm/3,75=1,92 i 3,2 cm/2,55=1,255. Zatem uwzględniając, że wykres jest malejący a=–1,92/1,255=–1,530. Pozostaje jedynie obliczyć przesunięcie wykresu w osi pionowej, a więc log(b). Korzystamy ze znajomości wartości funkcji C(R_S/R_O) w dowolnie wybranym jej punkcie. Niech to będzie punkt P2(1,100). Podstawiając te wartości do formuły opisującej funkcję mamy: log(100)=–1,53*log(1)+log(b), z czego wynika, że log(b)=log(100)–(–1,53)*log(1)=2+1,53*0=2.

Mamy już wszystkie dane do tego, by wyznaczyć ostateczną formułę opisującą charakterystykę. Konieczne są małe przekształcenia wyrażenia przedstawionego wcześniej (patrz - plik PDF).

Mikrokontroler mierząc zmieniającą się w zależności od stężenia gazu rezystancję R_S odnosi ją do znanej na podstawie kalibracji rezystancji R_O, a następnie korzystając z powyższej formuły oblicza stężenie gazu C wyrażane w jednostkach ppm. Na rysunku 8 przedstawiono weryfikację takiego obliczenia wykonaną w Excelu. Niebieski wykres powstał na podstawie danych o 5 punktach przeniesionych z PDF-a, czerwony wykres natomiast jest wynikiem obliczenia, które będzie wykonywał mikrokontroler stosując powyższą formułę. Jak widać niedokładności są niewielkie, a wynikają głównie z ograniczonej dokładności przenoszenia punktów z wykresu do arkusza i przyjętych przybliżeń. Drugim czynnikiem jest również fakt, że została zignorowana mała nieliniowość charakterystyki zamieszczonej w dokumentacji. Na rysunku 8 charakterystykę narysowano dla porównania w układzie liniowym i log-log.

Metoda 3 – pośrednie wyznaczenie formuły matematycznej

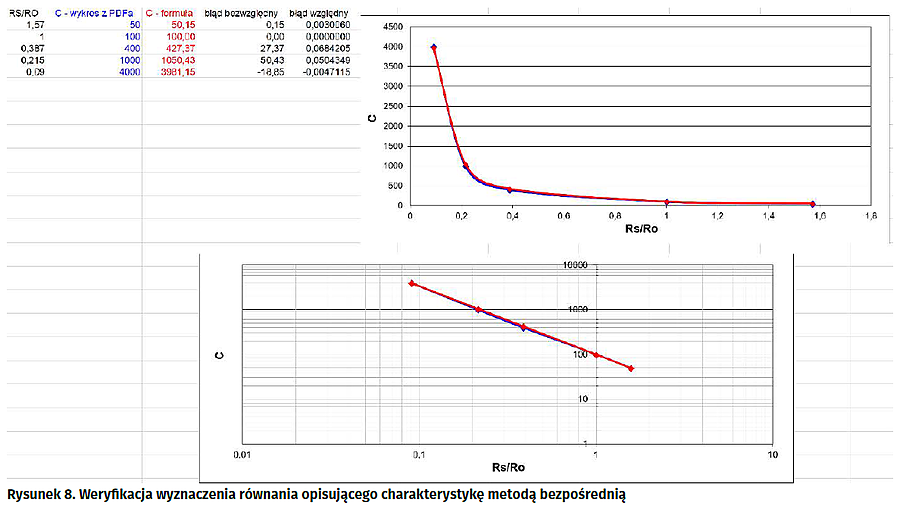
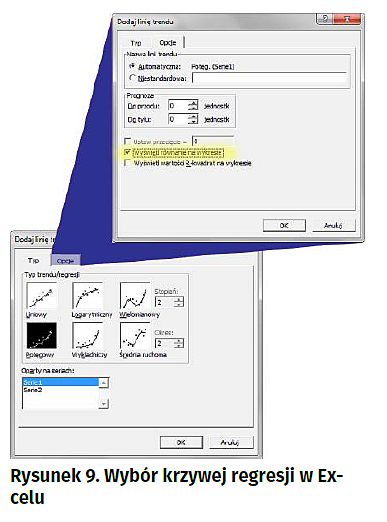
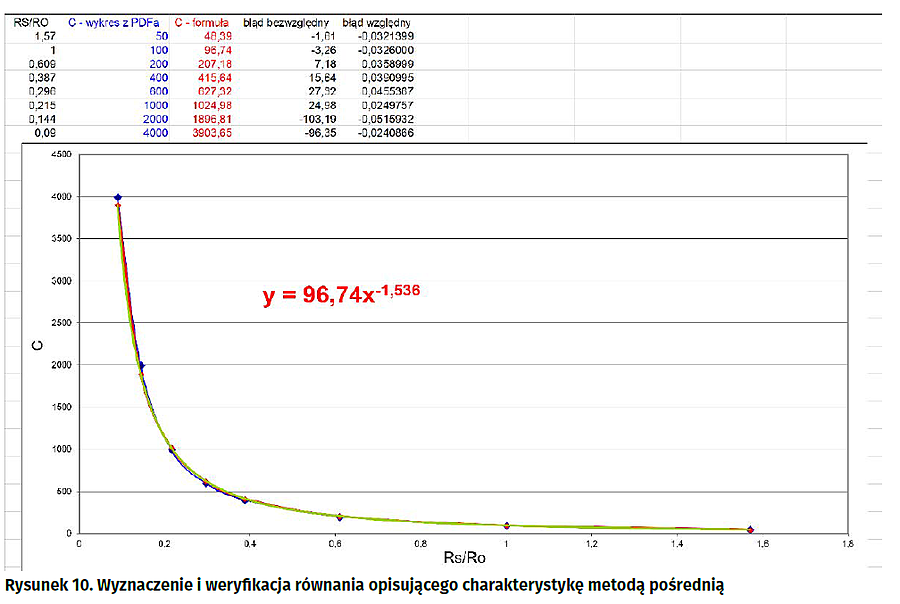
W tej metodzie skorzystamy również z Excela, przy czym tym razem nie będzie on weryfikował danych, a posłuży do wyznaczenia formuły opisującej wykres. Pierwszą czynnością jest przeniesienie danych do arkusza. To już potrafimy, co więcej mamy to już zrobione (rysunek 8). Przy takiej nieliniowości charakterystyki z jaką mamy do czynienia 5 punktów może się okazać liczbą niewystarczającą. Poznanymi metodami dodajmy jeszcze ze dwa, trzy punkty. Na przykład: P6(0,609, 200), P7(0,296, 600) i P8(0,144, 2000). Następnie tworzymy na podstawie tych punktów wykres punktowy z wygładzonymi liniami. Kolejną czynnością jest dodanie linii trendu typu potęgowego, koniecznie z opcją wyświetlania równania na wykresie (rysunek 9). Ostatecznie arkusz będzie zawierał dane liczbowe i wykresy, ale nas najbardziej będzie interesowało równanie opisujące linię trendu (rysunek 10). Linia ta z niezłą dokładnością odwzorowuje charakterystykę czujnika (patrz - plik PDF).

Otrzymane równanie ma prostszą postać niż to, które uzyskaliśmy w metodzie poprzedniej. Dokładność jest porównywalna, z tym, że do wyznaczenia równania w metodzie bezpośredniej wystarczyłyby zasadniczo dwa punkty, a w metodzie pośredniej warto wyznaczać ich jak najwięcej. Uzyskuje się wówczas widoczną poprawę dokładności, szczególnie na końcach wykresu.

Jak już było powiedziane osobnym zagadnieniem jest pomiar rezystancji czujnika, ale większym wyzwaniem jest bardzo duży przedział zmian mierzonych parametrów. W zależności od czujników może się on zawierać w dwóch, a nawet trzech dekadach. Należy wówczas myśleć o wprowadzeniu ręcznie lub automatycznie przełączanych zakresach pomiarowych urządzenia.

Jarosław Doliński, EP

Uwaga! Pełny tekst artykułu znajduje się w pliku PDF!