Pomiary charakterystyk częstotliwościowych (5). Filtry cyfrowe DSP typu IIR

01 kwietnia 2025

W piątej części cyklu podjęto próbę zmierzenia się z – wciąż nie do końca satysfakcjonującymi – rezultatami filtracji, oferowanymi przez transwersalne filtry cyfrowe (o skończonej odpowiedzi impulsowej – FIR). Dodatkowo pochylono się nad problematyką dokładniejszego pomiaru bardzo małych sygnałów, występujących przy silnym tłumieniu przebiegów wejściowych przez filtry. Fizycznej implementacji filtrów rekursywnych (o nieskończonej odpowiedzi impulsowej – IIR) ponownie dokonano z zastosowaniem modułu NUCLEO-STM32L432KC oraz dedykowanej płytki z towarzyszącymi filtrami analogowymi. Oczywiście podobnie jak poprzednio, charakterystyki wyznaczone symulacyjnie zostały przebadane pomiarowo.

W poprzednim odcinku kursu praktycznie zbadano koncepcję zastąpienia amplifiltrów analogowych za pomocą dość prostych filtrów cyfrowych typu FIR (ang. Finite Impulse Response), czyli filtrów o skończonej odpowiedzi impulsowej. Idea ta zrodziła się w oparciu o wnikliwą analizę niedoskonałości wspomnianych układów analogowych. Z kolei w podsumowaniu poprzedniego artykułu, jako wnioski z praktycznych rozważań nad niedoskonałościami badanych filtrów FIR oraz zastosowanych technik pomiarowych, zaznaczono dalsze kierunki poszukiwań rozwojowych. W szczególności poruszony został aspekt niesatysfakcjonujących charakterystyk częstotliwościowych względnie krótkich filtrów FIR oraz niedostatecznej dokładności pomiarów bardzo małych napięć na wyjściu filtru, tzn. przy jego znacznym tłumieniu.

Z ostatnim z wymienionych zagadnień spróbujemy zmierzyć się po prostu poprzez zastosowanie logarytmicznej sondy pomiarowej o znacznej dynamice. Natomiast większym wyzwaniem są zapewne niesatysfakcjonujące charakterystyki częstotliwościowe prostych filtrów FIR. Jednym z proponowanych wstępnie rozwiązań było znaczne wydłużenie projektowanych struktur FIR na drodze redukcji nakładu obliczeniowego per jednostkowy element filtru. Jakkolwiek po wnikliwym przeanalizowaniu kodu programu realizującego filtry okazało się, że potencjał tego rozwiązania to wydłużenie badanych filtrów o nie więcej niż 15...20%. Wg najlepszej wiedzy i doświadczenia inżynierskiego autora tej publikacji zapewne nie dałoby to radykalnej, w pełni satysfakcjonującej poprawy uzyskiwanych rezultatów filtracji.

Kolejnym rozważanym rozwiązaniem było obniżenie zastosowanej częstotliwości próbkowania Fs przy jednoczesnej optymalizacji właściwości analogowych (sprzętowych) filtrów: wejściowego i wyjściowego w opracowanym układzie pomiarowym. Tu z kolei również pole do manewru nie było znaczące (np. zmniejszenie Fs/2 z 24 kHz do 22 kHz, to około 10% dodatkowego czasu przetwarzania), ale za to potencjalne konsekwencje techniczne mogłyby być dość przykre (niestandardowa wartość Fs oraz bardzo mała odległość dopuszczalnej Fmax=20 kHz od Fs/2, implikująca konieczność stosowania dość ostrych, trudnych filtrów z uwagi na ryzyko wystąpienia aliasingu). Rozważano także użycie zaawansowanych bibliotek DSP z rodziny CMSIS [1, 2], wspieranych przez wykorzystywany w tym kursie procesor z rodziny ARM, jednak uznano, że uzysk obliczeniowy niekoniecznie byłby w pełni satysfakcjonujący, a na potrzeby edukacyjne warto jest pójść dalej inną drogą. W szczególności podjęto decyzję o zastosowaniu znacznie krótszych (więc i szybszych) filtrów rekursywnych IIR (ang. Infinite Impulse Response), czyli o (teoretycznie) nieskończonej odpowiedzi impulsowej. Dlatego właśnie w dalszej części pracy zaprezentowane zostały najpierw niezbędne podstawy teoretyczne działania filtrów IIR, a następnie – praktyczne projekty filtrów.

Oczywiście całość działań została zwieńczona kluczowymi dla tego kursu pomiarami, wraz z ich niezbędną interpretacją.

Zasada działania i projekty filtrów IIR

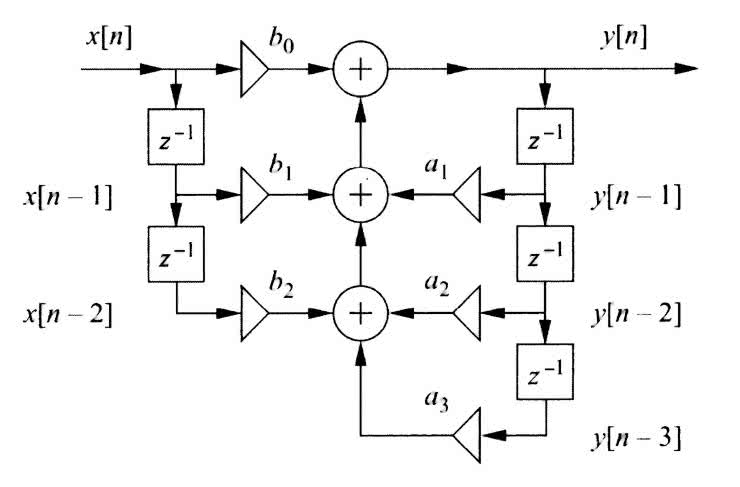
Na rysunku 55 pokazano schemat blokowy filtru rekursywnego [3]. Główną zaletą filtracji rekursywnej, w porównaniu z nierekursywną, jest możliwość osiągania bardziej stromych charakterystyk częstotliwościowych za pomocą mniejszej liczby wag.

Rysunek 55. Schemat blokowy filtru rekursywnego [3]

W tym przypadku każda próbka wyjściowa jest średnią ważoną pewnej liczby ostatnich próbek wejściowych oraz wyjściowych zgodnie ze wzorem (1):

y[n]=b₀x[n–0]+b₁x[n–1]+...+b_Mx[n–M]+a₁y[n–1]+...+a_Ny[n–N] (1)

W odniesieniu do przykładu z rysunku 55, na którym bloczek oznaczony „z^–1” jest tzw. członem opóźniającym, M=2 jest lizcbą opóźniających członów nierekursywnych, natomiast N=3 to liczba opóźniających członów rekursywnych. Jak widać, w filtrze występuje sprzężenie zwrotne, tzn. poprzednie próbki wyjściowe wpływają na wartość aktualnej próbki wyjściowej. Powoduje to, że filtr może być niestabilny. Dlatego wartości jego wag b[m] oraz a[k] należy dobierać jeszcze staranniej niż w filtrach nierekursywnych.

Podane informacje teoretyczne zasadniczo wystarczają do praktycznej implementacji prostych filtrów IIR. Projekty filtrów IIR, podobnie jak to było w przypadku filtrów FIR, opracowano w dostępnym bezpłatnie środowisku Octave [4]. Listing 1 prezentuje zawartość skryptu w języku środowiska Octave, którego użyto do wygenerowania współczynników projektowanych filtrów IIR.

clc; %% cleaning the workspace
pkg load signal; %% load signal processing package

scale=2^12 %% scaling factor
Nord=3 %% IIR filter order
Fs2=24.0 %% Fs/2 [kHz]

%% LPF
disp(„LPF”);
[b, a] = butter(Nord, 2.7/Fs2, „low”);
b=round(scale*b); a=round(scale*a);
figure(1); freqz(b/scale, a/scale);
disp(b); disp(a);

%% HPF
disp(„HPF”);
Fs2=24.0; %% Fs/2 [kHz]
[b, a] = butter(Nord, 3.0/Fs2, „high”);
b=round(scale*b); a=round(scale*a);
figure(2); freqz(b/scale, a/scale);
disp(b); disp(a);

%% BPF
disp(„BPF”);
Fs2=24.0; %% Fs/2 [kHz]
[b, a] = butter(Nord, [0.31/Fs2, 3.1/Fs2], „bandpass”);
b=round(scale*b); a=round(scale*a);
figure(3); freqz(b/scale, a/scale);
disp(b); disp(a);

%% „peak”
disp(„PEAK filter”);
Fs2=24.0; %% Fs/2 [kHz]
[b, a] = butter(Nord, [18.5/Fs2, 19.5/Fs2], „bandpass”);
b=round(scale*b); a=round(scale*a);
figure(4); freqz(b/scale, a/scale);
disp(b); disp(a);

%% „notch”
disp(„NOTCH filter”);
Fs2=24.0; %% Fs/2 [kHz]
[b, a] = butter(Nord, [18.5/Fs2, 19.5/Fs2], „stop”);
b=round(scale*b); a=round(scale*a);
figure(5); freqz(b/scale, a/scale);
disp(b); disp(a);

Listing 1.

Kluczową funkcją, użytą do wygenerowania przedmiotowych filtrów, jest funkcja [b, a] = butter(n, wc, filter_type). Wyciąg z opisu użytecznych tutaj sposobów jej parametryzacji ujęto na listingu 2.

Function File: [b, a] = butter (n, wc, filter_type)
Generate a Butterworth filter. Default is a discrete space (Z) filter. The cutoff frequency, wc should be specified in radians for analog filters. For digital filters, it must be a value between zero and one. For bandpass filters, wc is a two-element vector with w(1) < w(2). The filter type must be one of „low”, „high”, „bandpass”, or „stop”. The default is „low” if wc is a scalar and „bandpass” if wc is a two-element vector.
Low pass filter with cutoff pi*Wc radians:
[b, a] = butter (n, Wc)
High pass filter with cutoff pi*Wc radians:
[b, a] = butter (n, Wc, „high”)
Band pass filter with edges pi*Wl and pi*Wh radians:
[b, a] = butter (n, [Wl, Wh])
Band reject filter with edges pi*Wl and pi*Wh radians:
[b, a] = butter (n, [Wl, Wh], „stop”)

Listing 2.

Parametry: Wc, Wl i Wh stanowią wartości częstotliwości granicznych (0…1), wyrażonych względem połowy częstotliwości próbkowania Fs/2. W przypadku prostych filtrów LPF oraz HPF (parametryzowanych odpowiednio jako: low oraz high) wykorzystuje się wyłącznie jeden parametr Wc, natomiast w implementacjach bardziej złożonych filtrów BPF, peak oraz notch (parametryzowanych odpowiednio jako: bandpass oraz stop) – stosuje się obligatoryjnie dwa parametry: Wl i Wh, przy czym obowiązkowo musi zachodzić warunek: Wl < Wh. Do wygenerowania tutaj filtru typu notch zastosowano model parametryzacji typu bandpass z odpowiednio wąskim przedziałem zadanych częstotliwości. Funkcja butter(…) generuje filtry wg tzw. aproksymacji Butterwortha, czyli maksymalnie płaskie. Nie oferuje ona co prawda tak dużej stromości zboczy, jak np. aproksymacja Bessela czy Czebyszewa, jednak minimalizuje zafalowania pasma przenoszenia generowanych filtrów.

Jak wynika z listingu 1, jako częstotliwość próbkowania ponownie przyjęto Fs=48 kHz, natomiast jako rząd filtru w przypadku wszystkich projektów zadano N_ord=3. Współczynnik skalujący scale został użyty w celu dostosowania wartości uzyskanych współczynników b[n] oraz a[n] do arytmetyki całkowitoliczbowej, którą także w tej części kursu użyto w implementacji fizycznej. Warto w tym miejscu podkreślić, że w trakcie eksperymentów z projektowaniem filtrów różne wartości parametru N_ord były optymalne dla różnych typów generowanych filtrów, jednak z punktu widzenia tego kursu nie jest to kluczowe zagadnienie.

Listing 3 prezentuje wartości współczynników b[n] oraz a[n] wygenerowanych filtrów IIR. Liczby elementów w poszczególnych ciągach współczynników wynoszą odpowiednio: N_ord+1 dla filtrów prostych (LPF oraz HPF) oraz 2·N_ord+1 w przypadku filtrów pasmowych (BPF, peak, notch) co należy rozumieć tak, że te drugie filtry są niejako złożeniem pary filtrów prostych.

LPF
16 49 49 16
4096 -9407 7454 -2012
HPF
2759 -8276 8276 -2759
4096 -9090 7025 -1858
BPF
18 0 -54 0 54 0 -18
4096 -21420 46912 -55126 36681 -13108 1965
PEAK filter
1 0 -3 0 3 0 -1
4096 18687 39662 48629 36345 15691 3152
NOTCH filter
3593 17140 38034 48727 38034 17140 3593
4096 18687 39662 48629 36345 15691 3152

Listing 3.

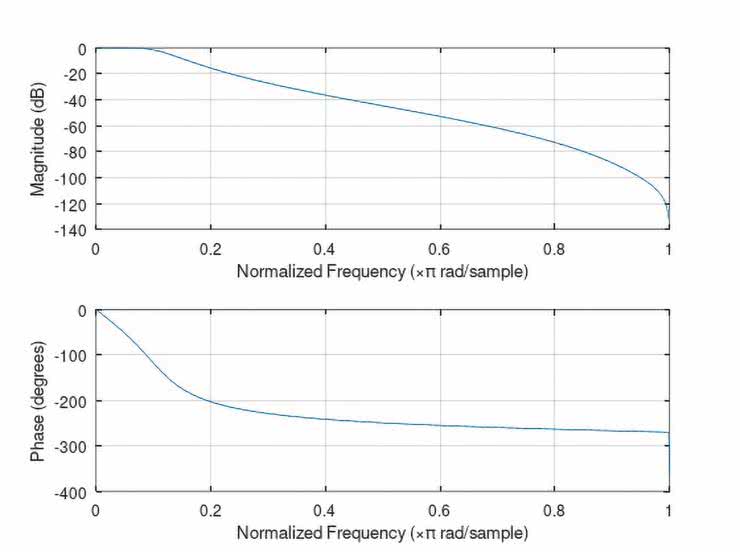
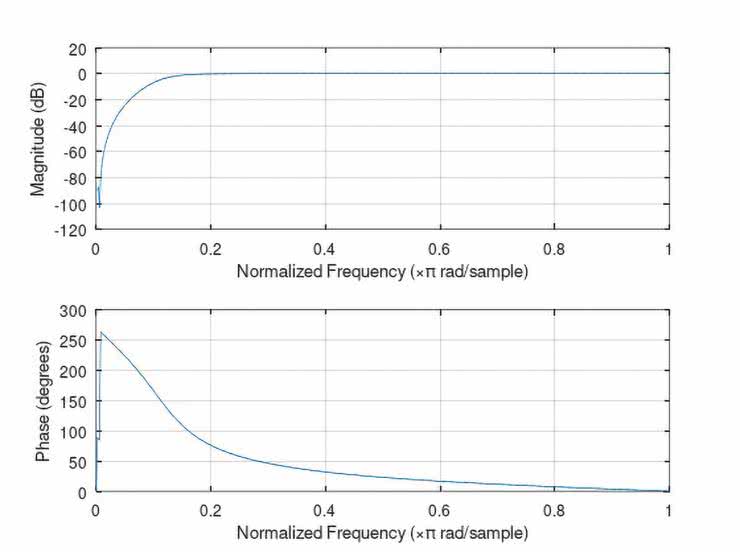
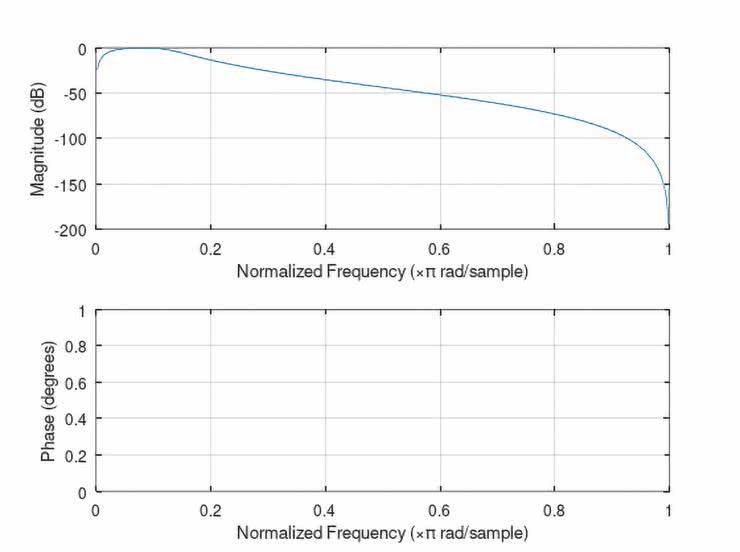
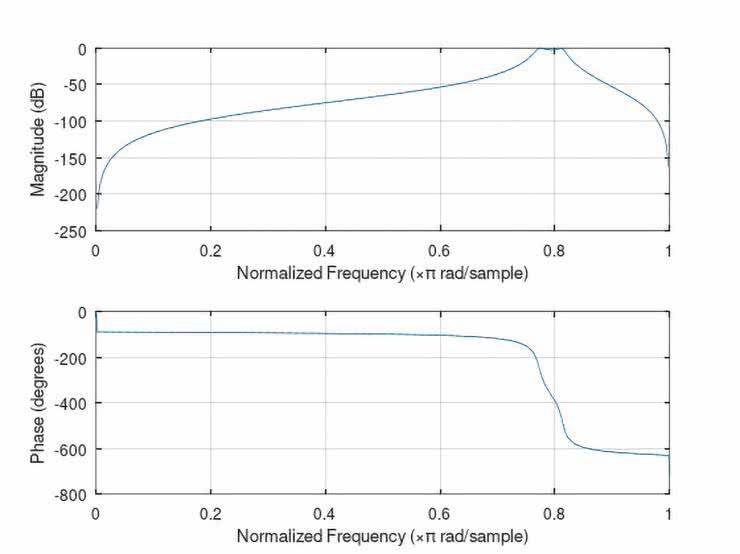
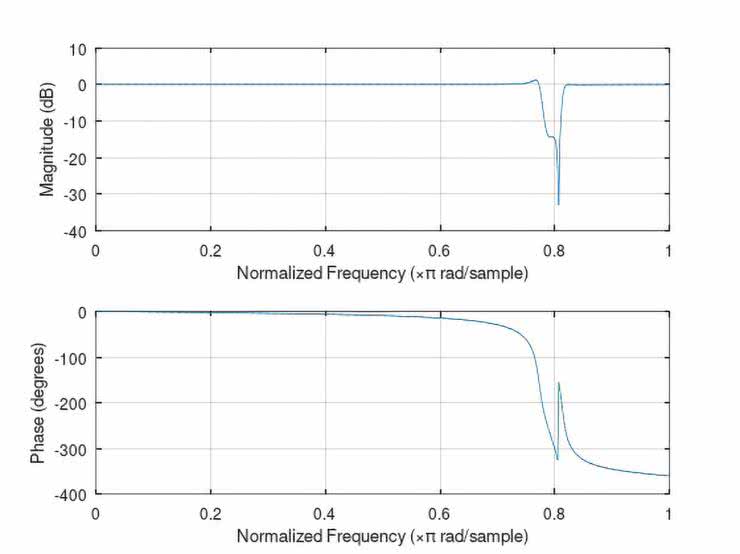
Na rysunkach 56…60 zaprezentowano zasymulowane, pełne charakterystyki częstotliwościowe (amplitudowe i fazowe) wszystkich zaprojektowanych rekursywnych filtrów (IIR): dolnoprzepustowego LPF, górnoprzepustowego HPF, pasmowoprzepustowego BPF oraz wąskopasmowych typu peak oraz notch. Pomimo, że wymagane parametry charakterystyk częstotliwościowych były praktycznie identyczne, jak w przypadku omawianych w poprzednim odcinku cyklu analogicznych filtrów transwersalnych FIR, a rzędy filtrów IIR były znacznie niższe od tych zastosowanych w implementacjach FIR, to charakterystyki amplitudowe tych drugich (IIR) były znacznie bardziej strome. Oczywiście jest tak z uwagi na występujące w filtrach IIR (rekursywnych) sprzężenie zwrotne (nie ma go w filtrach transwersalnych FIR).

Rysunek 56. Charakterystyki częstotliwościowe i fazowe filtru IIR LPF (symulacja)

Rysunek 57. Charakterystyki częstotliwościowe i fazowe filtru IIR HPF (symulacja)

Rysunek 58. Charakterystyki częstotliwościowe i fazowe filtru IIR BPF (symulacja)

Rysunek 59. Charakterystyki częstotliwościowe i fazowe filtru IIR peak (symulacja)

Rysunek 60. Charakterystyki częstotliwościowe i fazowe filtru IIR notch (symulacja)

Jakkolwiek wspomniane zalety filtrów IIR są też okupione bardzo poważnymi wadami:

w przeciwieństwie do filtrów FIR nie gwarantują one liniowości fazy charakterystyki częstotliwościowej (a więc także stałości opóźnienia grupowego, co może być istotną wadą w niektórych zastosowaniach, np. pomiarowych),
w przeciwieństwie do filtrów FIR nie gwarantują one stabilności, co (w największej ogólności) znacznie utrudnia zarówno samo projektowanie, jak i „bezpieczną” implementację fizyczną filtrów IIR. Potencjalna niestabilność tej topologii wynika z występowania w niej sprzężenia zwrotnego i może objawić się choćby na skutek numerycznych niedokładności przetwarzania (szum numeryczny może pobudzać pętlę sprzężenia zwrotnego do pracy jako generator, niestety).

Programowa realizacja filtrów cyfrowych IIR została zaimplementowana tutaj wg ram poniższego, prostego algorytmu:

Jednorazowe zdefiniowanie w kodzie programu MCU współczynników b[n] i a[n] filtru IIR oraz dwóch odpowiadających im buforów („B” i „A”) – rejestrów przesuwnych FIFO do przechowywania pobranych próbek sygnału wejściowego oraz próbek sygnału wyjściowego.
Zainicjalizowanie w MCU bloków peryferiów GPIO, ADC oraz DAC i wyznaczenie składowej stałej na wejściu ADC (tzw. offset – do usunięcia z pobranych próbek w kolejnych krokach obliczeniowych).
Wykonywanie w nieskończonej pętli następujących kroków:

zlecenie ADC pobrania kolejnej próbki sygnału wejściowego,
przesunięcie bufora – rejestru FIFO „B” próbek wejściowych o jedną próbkę, „gubiące” najstarszą próbkę na końcu rejestru i przygotowujące miejsce na wpis nowej próbki na jego początku,
odczyt nowej próbki z ADC i zapis do rejestru FIFO „B” (próbek wejściowych),
przeliczenie wyjścia filtru IIR wg zależności (1),
przesunięcie bufora – rejestru FIFO „A” próbek wyjściowych o jedną próbkę, „gubiące” najstarszą próbkę na końcu rejestru i przygotowujące miejsce na wpis nowej próbki na jego początku,
zapamiętanie na początku rejestru FIFO „A” (próbek wyjściowych) nowo wyliczonej wartości na wyjściu filtru IIR,
zapis wyliczonej wartości wyjścia filtru IIR do przetwornika DAC w MCU,
powrót na początek nieskończonej pętli III.

Oprogramowanie opracowano i skompilowano w środowisku STM32CubeIDE [5], dostarczanym bezpłatnie przez producenta mikrokontrolerów STM32, firmę ST Microelectronics.

Pomiary opracowanych filtrów IIR

Rysunek 61 prezentuje schemat blokowy zastosowanego toru pomiarowego. Platformę sprzętową do testów, której sercem jest mikrokontroler STM32L432KC, osadzony na 30-pinowym module NUCLEO-STM32L432KC [6, 7, 8], zrealizowano wg niemal identycznej koncepcji, jak to miało miejsce w przypadku testów filtrów FIR i dlatego nie będzie ona tutaj szerzej omawiana. W szczególności zastosowano te same analogowe filtry: wejściowy i wyjściowy. Natomiast jedyną (ale istotną) różnicą było użycie innego ustroju pomiarowego, a mianowicie prosty oscyloskop cyfrowy o stosunkowo niskiej, 8-bitowej rozdzielczości przetwornika ADC (a – w konsekwencji – oferującego niską dokładność przetwarzania) służył jedynie do kontroli obecności i kształtu sygnału wyjściowego. Jako zasadniczy przyrząd pomiarowy zastosowano sondę logarytmiczną o dużej dynamice przetwarzania wg projektu AVT5991 [9] oraz półautomatyczny woltomierz cyfrowy. Sonda została uprzednio skalibrowana i wyskalowana tak, że przy napięciu wejściowym sinusoidalnym Uwe=1 Vp-p o częstotliwości F=1 kHz, przetworzone logarytmicznie napięcie stałe na wyjściu sondy wynosiło Uwy=2,2 V. Dodatkowo zmiana zmiennego napięcia wejściowego Uwe o 1 dB skutkowała zmianą stałego napięcia wyjściowego Uwy o 10 mV (czyli współczynnik przetwarzania sondy wynosił 10 mV/dB). Ostatecznie zastosowanie w pomiarach półprofesjonalnej sondy logarytmicznej zaowocowało znacznym zwiększeniem dynamiki i dokładności realizowanych pomiarów.

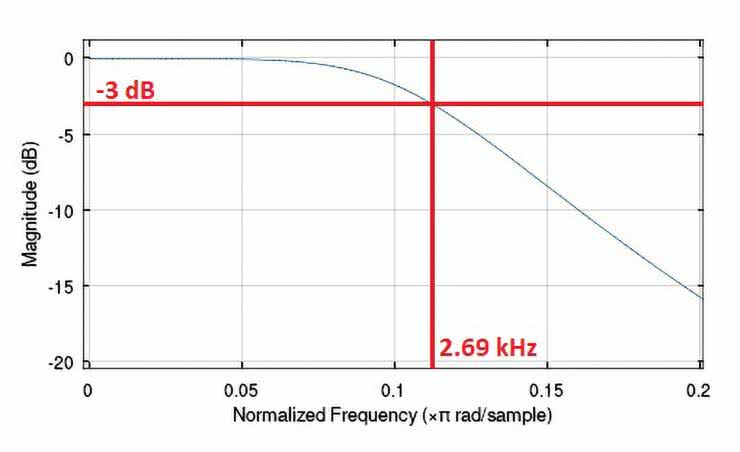
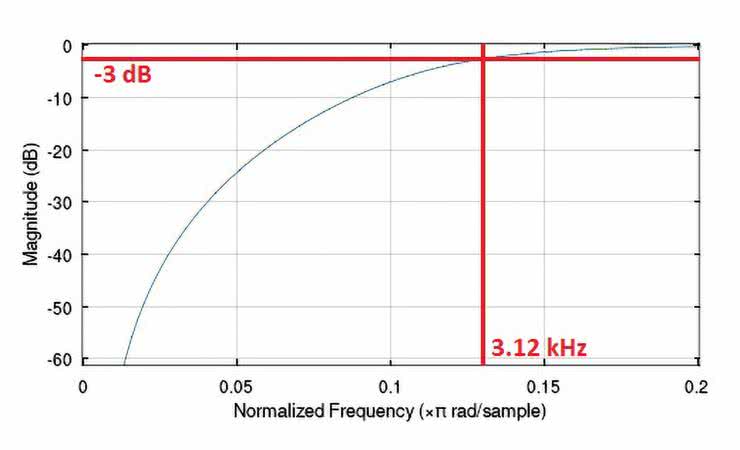
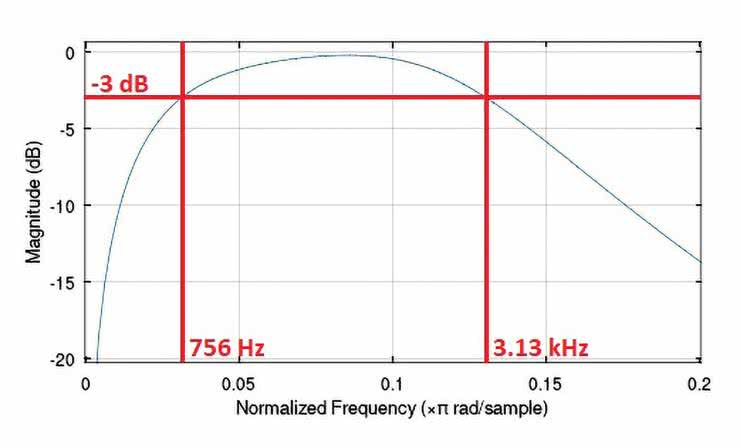
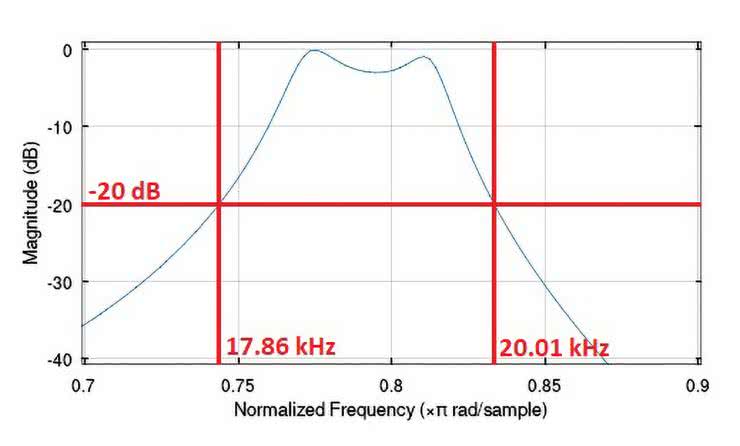
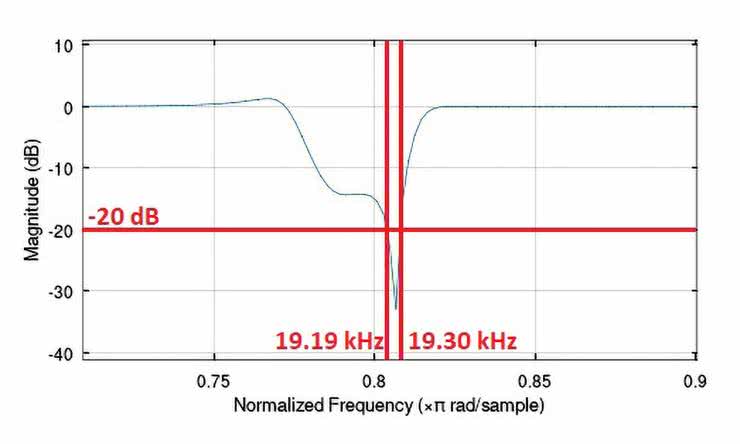
Rysunek 61. Schemat blokowy zastosowanego toru pomiarowego

Na rysunkach 62...66 pokazano zasymulowane komputerowo charakterystyki częstotliwościowe przebadanych filtrów, przy czym powiększono najbardziej interesując, a zarazem najistotniejsze zakresy ich zmienności. Dodatkowe opisy wartości na osi częstotliwości mają na celu ułatwienie ich analizy i interpretacji, ponieważ nominalnie program Octave skaluje oś częstotliwości wykresów wartością znormalizowaną względem połowy częstotliwości próbkowania Fs/2.

Rysunek 62. Zasymulowana charakterystyka częstotliwościowa filtru IIR LPF (zbliżenie)

Rysunek 63. Zasymulowana charakterystyka częstotliwościowa filtru IIR HPF (zbliżenie)

Rysunek 64. Zasymulowana charakterystyka częstotliwościowa filtru IIR BPF (zbliżenie)

Rysunek 65. Zasymulowana charakterystyka częstotliwościowa filtru IIR peak (zbliżenie)

Rysunek 66. Zasymulowana charakterystyka częstotliwościowa filtru IIR notch (zbliżenie)

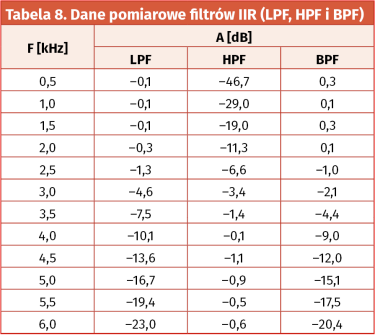
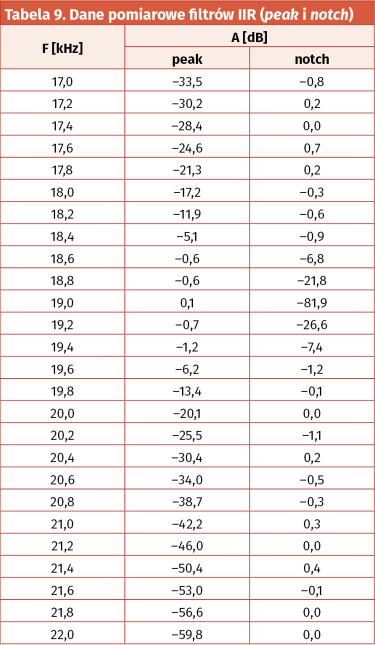
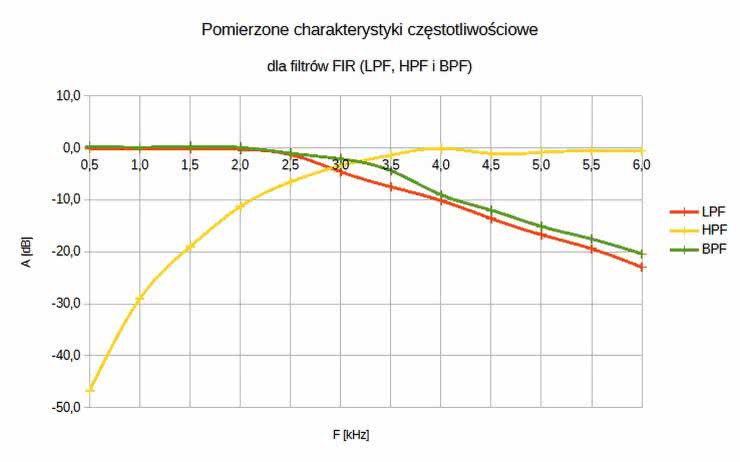
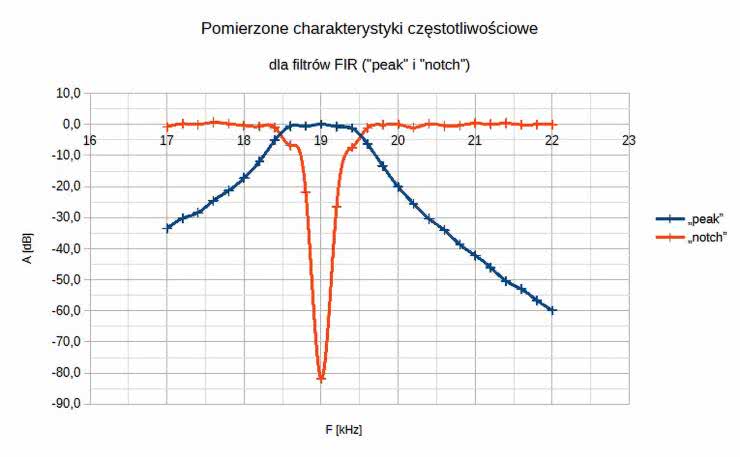
Z kolei rezultaty fizycznych pomiarów tychże charakterystyk częstotliwościowych badanych filtrów ujęto w tabelach 8 i 9 (dane liczbowe) oraz na wykresach, zamieszczonych na rysunkach 67 i 68.

W tym przypadku, przy względnie niewielkich błędach pomiarowych, uzyskano całkiem satysfakcjonującą zgodność rezultatów pomiaru charakterystyk filtrów cyfrowych IIR z wynikami teoretycznych symulacji komputerowych ich prototypów. Dalszą, dokładną analizę porównawczą zaprezentowanych danych polecam uwadze wnikliwych Czytelników.

Rysunek 67. Zmierzone charakterystyki częstotliwościowe filtrów IIR (LPF, HPF i BPF)

Rysunek 68. Zmierzone charakterystyki częstotliwościowe filtrów IIR (peak i notch)

Podsumowanie i wnioski

W artykule zaprezentowano teoretyczne podstawy praktycznej realizacji cyfrowych filtrów rekursywnych (IIR), czyli o nieskończonej odpowiedzi impulsowej. Następnie pokazano projekty pięciu różnych filtrów o wymaganych parametrach zbliżonych do parametrów prezentowanych wcześniej amplifiltrów analogowych oraz transwersalnych filtrów cyfrowych (FIR) – o skończonej odpowiedzi impulsowej. Przeprowadzone pomiary fizycznych realizacji zaprojektowanych komputerowo filtrów IIR wykazały całkiem satysfakcjonującą zgodność z ich teoretycznymi prototypami. Artykuł stał się również pretekstem do przeprowadzenia dyskusji porównawczej nad właściwościami (wadami i zaletami) filtrów cyfrowych typu FIR oraz IIR. Wnioski z przeprowadzonych badań i analiz zostaną zapewne w przyszłości wykorzystane do planowanej przez autora publikacji projektu mini-kombajnu pomiarowego DSP. W kolejnych odcinkach tego cyklu edukacyjnego autor zamierza pochylić się nad pomiarami analogowych torów liniowych fizycznych urządzeń m.cz. oraz w.cz.

Adam Sobczyk, EP

Literatura:

What is CMSIS?, https://www.keil.arm.com/cmsis
CMSIS Ver. 6.1.0, https://arm-software.github.io/CMSIS_6/latest/General/index.html
Cyfrowe przetwarzanie sygnałów w telekomunikacji. Podstawy. Multimedia. Transmisja, Praca zbiorowa pod redakcją naukową: Tomasz P. Zieliński oraz Przemysław Korohoda i Roman Rumian, Wydawnictwo Naukowe PWN SA, Warszawa 2014, Wyd. 1,
Signal processing tools, including filtering, windowing and display functions, https://octave.sourceforge.io/signal/overview.html
Zasoby dotyczące środowiska programistycznego STM32CubeIDE, https://www.st.com/en/development-tools/stm32cubeide.html
STM32L432KB STM32L432KC. Datasheet – production data, www.st.com, May 2018, DS11451, Rev. 4
UM1956. User manual. STM32 Nucleo-32 boards (MB1180), November 2018, Rev. 5
UM1884. User manual. Description of STM32L4/L4+ HAL and low-layer drivers, www.st.com, September 2021, Rev. 9
Sonda logarytmiczna z układem AD8307, https://serwis.avt.pl/manuals/AVT5991.pdf