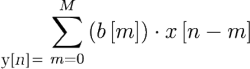Jak wspomniano powyżej, idea zastąpienia amplifiltrów analogowych za pomocą względnie nieskomplikowanych filtrów cyfrowych typu FIR (ang. Finite Impulse Response, czyli filtrów o skończonej odpowiedzi impulsowej, zwanych także filtrami transwersalnymi) zrodziła się przede wszystkim w oparciu o wnioski z wcześniejszych części tego cyklu publikacji. W szczególności satysfakcjonująca implementacja filtrów analogowych o dość wyśrubowanych parametrach wymagały zastosowania elementów RC o dużej dokładności (więc i małej tolerancji), a stabilność i powtarzalność uzyskiwanych parametrów wymagała także znacznej staranności implementacji fizycznej układu.
Szczególnie wyraźnie zagadnienia te dotyczyły filtrów wąskopasmowych o znacznej dobroci (typu „peak” oraz „notch”). O ile skuteczna implementacja rozwiązań z dziedziny DSP (ang. Digital Signal Processing, czyli cyfrowego przetwarzania sygnałów) także stawia przed konstruktorem liczne wymagania i obostrzenia, o tyle jednak kusząca jest względna łatwość ich programowej implementacji na jednolitej, powtarzalnej platformie sprzętowej w przypadku wszystkich omawianych filtrów. Dodatkową zachętą okazała się możliwość skorzystania w tym celu z popularnego, łatwo dostępnego (i to w przystępnej cenie), niewielkiego modułu NUCLEO-STM32L432KC produkcji firmy ST Microelectronics w postaci PCB o rozmiarze Arduino Nano. Wstępna analiza właściwości przedmiotowego modułu z mikrokontrolerem STM32L432KC wykazała potencjalną przydatność do realizacji podstawowych technik DSP w zastosowaniach z dziedziny m.cz., czyli głównie audio. Zaważyła o tym przede wszystkim dostępność na jego pokładzie dostatecznie szybkich bloków peryferyjnych: wielokanałowego przetwornika analogowo-cyfrowego (ADC) oraz dwóch przetworników cyfrowo-analogowych (DAC), a także wsparcie sprzętowe dla instrukcji obliczeniowych DSP, dostępne standardowo w MCU z rdzeniem ARM Cortex-M4.
Teoretyczne podstawy DSP w pigułce
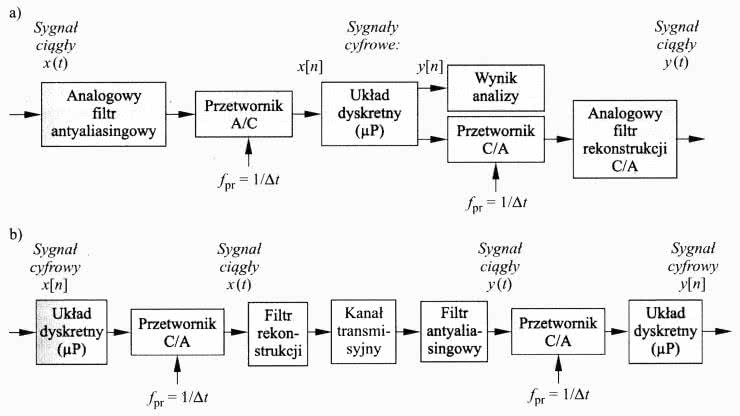
Zasadniczo celem tej publikacji nie jest szczegółowe omawianie licznych zagadnień z rozległej dziedziny cyfrowego przetwarzania sygnałów, jakkolwiek autor niniejszego opracowania poczuł się w obowiązku przedstawić w tym miejscu przynajmniej minimalne teoretyczne podstawy DSP, wykorzystywane dalej na potrzeby rozpatrywanych rozwiązań praktycznych i wprowadzane na bieżąco razem z nimi. Na rysunku 34 [1] zaprezentowano dwie klasyczne koncepcje cyfrowych torów analizy i przetwarzania sygnałów: analog-cyfra-analog (a) oraz cyfra-analog-cyfra (b). Na ilustracjach użyto następujących oznaczeń: ∆t – okres próbkowania, fpr – częstotliwość próbkowania. W kontekście tej publikacji nie będzie nas interesował przypadek (b), który z definicji opisuje koncepcję fizycznej realizacji cyfrowego kanału teletransmisyjnego, działającego w oparciu o analogowe medium fizyczne, zatem skupimy się na schemacie blokowym z przypadku (a).
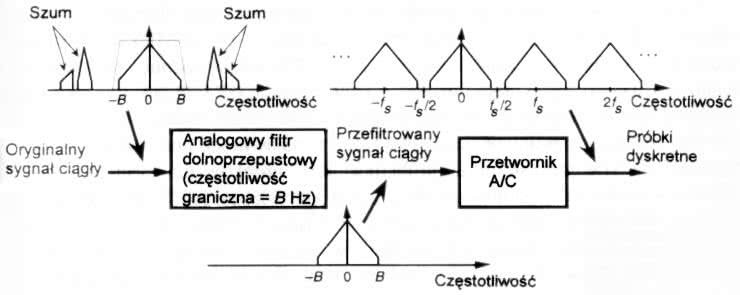
Jak widać, oprócz umieszczonego centralnie układu przetwarzania wartości dyskretnych (czyli zazwyczaj układu mikroprocesorowego, μP) oraz przetworników A/C (ADC) i C/A (DAC), niezbędnych do obróbki sygnałów w pełni analogowych (tzn. ciągłych w dziedzinie czasu i wartości fizycznych), na wejściu układu znajdują się także analogowy filtr antyaliasingowy, a na wyjściu toru – analogowy filtr rekonstrukcji. Pierwszy z tych bloków jest niezbędny z uwagi na ryzyko wystąpienia zjawiska aliasingu, czyli pasożytniczego przenikania do spróbkowanego sygnału powielonego widma sygnału użytecznego, powtarzanego wokół całkowitych wielokrotności częstotliwości próbkowania ±n∙Fs (n=1, 2, …). Zjawisko aliasingu występuje wtedy, gdy nie jest spełnione tzw. kryterium Nyquista, tzn. Fmax (najwyższa częstotliwość występująca w próbkowanym sygnale analogowym) nie jest niższa (najlepiej z odpowiednim zapasem) od Fs/2:
Fmax<Fs/2 (1)
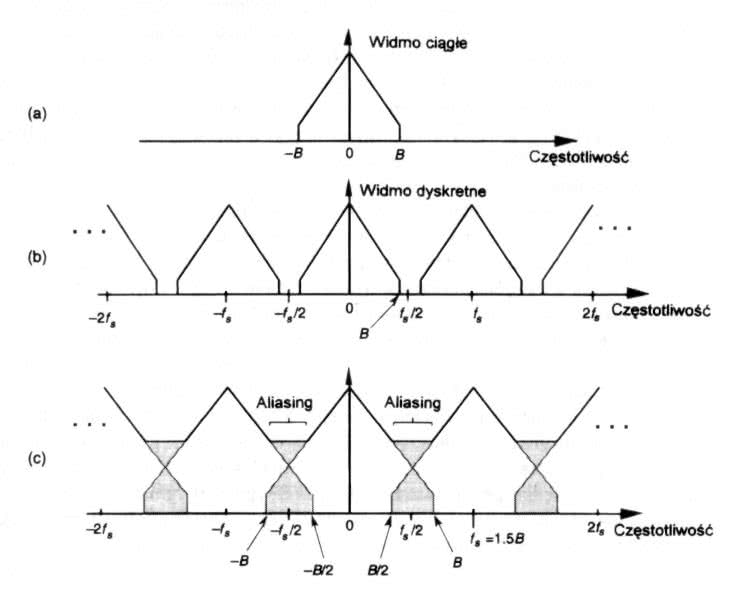
Na rysunku 35 [2] zilustrowano zjawisko powielania widmowego. Wykres (a) prezentuje widmo ciągłe dolnopasmowego sygnału o paśmie B, natomiast wykresy (b) i (c) prezentują kolejno: powielanie widmowe sygnału spróbkowanego w przypadku Fs/2 > B oraz powielanie i nakładanie widm spowodowane faktem, że szybkość próbkowania jest zbyt mała (zachodzi warunek Fs/2 < B, występuje zatem nakładanie się częstotliwości i aliasing).
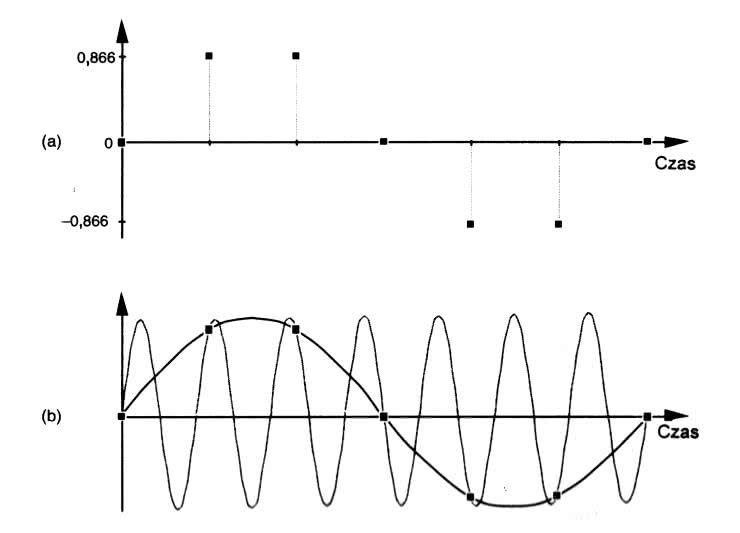
Filtry ograniczające pasmo przetwarzanego sygnału analogowego zapobiegają także skutkom występowania zjawiska niejednoznaczności częstotliwości. Rysunek 36 [2] wyjaśnia istotę tego zjawiska: na wykresie (a) widzimy dyskretny ciąg próbek, natomiast wykres (b) pokazuje dwa różne przebiegi sinusoidalne, które mogłyby być potencjalnie reprezentowane przez ten sam ciąg próbek z wykresu (a).
Z kolei rysunek 37 [2] objaśnia celowość stosowania wstępnych, dolnoprzepustowych filtrów przetwarzanego sygnału analogowego z uwagi na ryzyko przedostawania się do przebiegu spróbkowanego zakłóceń spoza pasma B sygnału użytecznego – także w rezultacie występowania powielania widmowego. Jak łatwo domyśleć się, z powodu występowania opisanych zjawisk również sygnał analogowy na wyjściu systemu przetwarzania wg rysunku 34 – odtworzony np. za pomocą prostokątnych próbek sygnału – powinien zostać poddany analogicznej filtracji dolnoprzepustowej. Szczegółowy opis ilościowy wymienionych zjawisk istotnie wykracza jednak poza podstawowy zakres i cel tego opracowania.
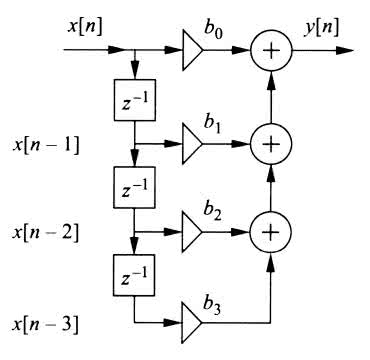
Jako „układ dyskretny (μP)”, realizujący przetwarzanie sygnału cyfrowego x[n] na y[n] (rysunek 34a) w pierwszym, stosunkowo najprostszym implementacyjnie podejściu zaproponowano filtr cyfrowy typu FIR (transwersalny lub inaczej nierekursywny), czyli o skończonej odpowiedzi impulsowej. W przeciwieństwie do filtrów rekursywnych IIR (ang. Infinite Impulse Response), czyli o nieskończonej odpowiedzi impulsowej, filtry FIR cechuje gwarantowana stabilność, wynikająca z braku gałęzi sprzężenia zwrotnego. Oznacza to także uproszczenie realizacji praktycznej oraz procesów projektowania i analizy właściwości. Niestety ceną, jak trzeba zapłacić za te ewidentne zalety, jest potencjalnie znacznie większy nakład obliczeniowy, potrzebny do realizacji filtrów FIR, a wynikający z istotnie większej liczby bloków opóźniających oraz elementów mnożących niż w przypadku równoważnego funkcjonalnie filtru IIR. Pomimo to zadanie zastąpienia prototypów analogowych w technice DSP rozpoczniemy od realizacji opartej właśnie na (prostsze) filtrach FIR. Rysunek 38 [1] pokazuje klasyczną implementację takiego filtru rzędu M=3.
Bloczki oznaczone „z–1” są układami opóźniającymi o jedną próbkę, natomiast bloczki oznaczone jako b0...b3 to człony mnożące (skalujące) wartości kolejnych czterech próbek. Moduły „z–1” realizują swego rodzaju rejestr przesuwny typu FIFO (ang. First Input First Output), w którym nowsze próbki zastępują te wcześniej pobrane wg symbolicznej zależności x’[n–1]=x[n], a najstarsza próbka nieodwracalnie opuszcza rejestr. Ciąg współczynników b0...b3 jednoznacznie definiuje właściwości filtru FIR, a jego długość jest zawsze o jeden większa od rzędu filtru. I tak na wyjściu filtru FIR uzyskujemy sygnał y[n] będący sumą liczoną wg wzoru:
Podane informacje teoretyczne zasadniczo wystarczą do implementacji praktycznej naszych prostych filtrów FIR, lecz zostaną rozszerzone w kolejnej części tego cyklu publikacji.
Platforma sprzętowa
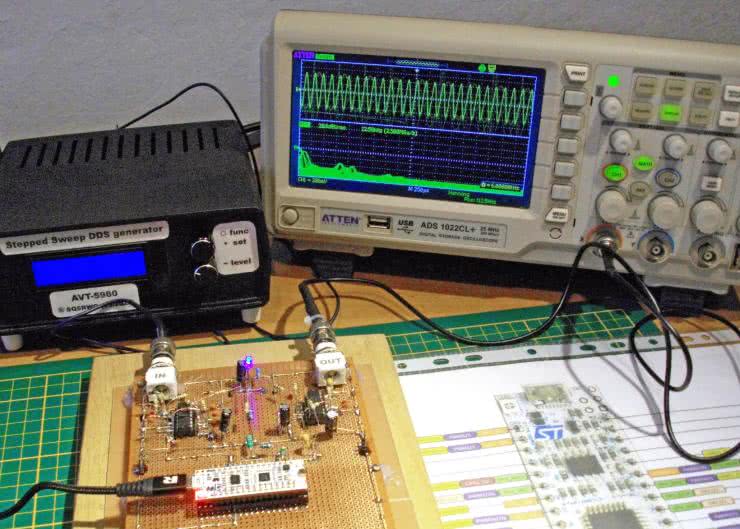
Platformę sprzętową, niezbędną do przeprowadzenia opisanych dalej badań, zrealizowano z podziałem na dwie główne części. Odnosząc się do schematu blokowego z rysunku 34a, możemy powiedzieć, że pierwsza, zasadnicza część obejmująca bloki: przetwornika ADC, układu dyskretnego (μP) oraz przetwornika DAC, została zrealizowana w oparciu na zasobach wewnętrznych mikrokontrolera STM32L432KC, osadzonego w 30-pinowym module NUCLEO-STM32L432KC, pokazanym na fotografii 5 [3].
Zastosowany mikrokontroler [4] był taktowany wewnętrznym zegarem, pracującym z maksymalną dopuszczalną dla tego MCU częstotliwością taktowania Fclk=80 MHz, przy czym źródłowy zegar wewnętrzny MSI był synchronizowany z zewnętrznym rezonatorem kwarcowym, pracującym z zegarem LSE o częstotliwości 32,768 kHz. Zasoby obliczeniowe zastosowanego MCU oraz ustalona częstotliwość Fclk pozwoliły na implementację całkowitoliczbowych filtrów FIR o maksymalnym rzędzie równym 26 lub 27 (zależnie od podtypu filtru) przy częstotliwości próbkowania Fs=48 kHz (implementacje filtrów z zastosowaniem liczb zmiennoprzecinkowych typu float były znacznie wolniejsze). Uzyskana częstotliwość Fs pozwoliła na pracę przyrządu z sygnałami analogowymi „monochromatycznymi” (czysta sinusoida) o częstotliwości maksymalnej Fmax=20 kHz, co zgadza się z kryterium Nyquista [1, 2] (Fmax < Fs/2=24 kHz). Poza pinami zasilania (+3,3 V) i masy (GND) zastosowano oczywiście także: wejście przetwornika ADC1/8 (pin A3 modułu NUCLEO) oraz wyjście przetwornika DAC1 (pin A4 modułu NUCLEO). Moduł NUCLEO był cały czas zasilany z portu USB komputera PC, ten sam interfejs umożliwiał także programowanie i debugowanie procesora.
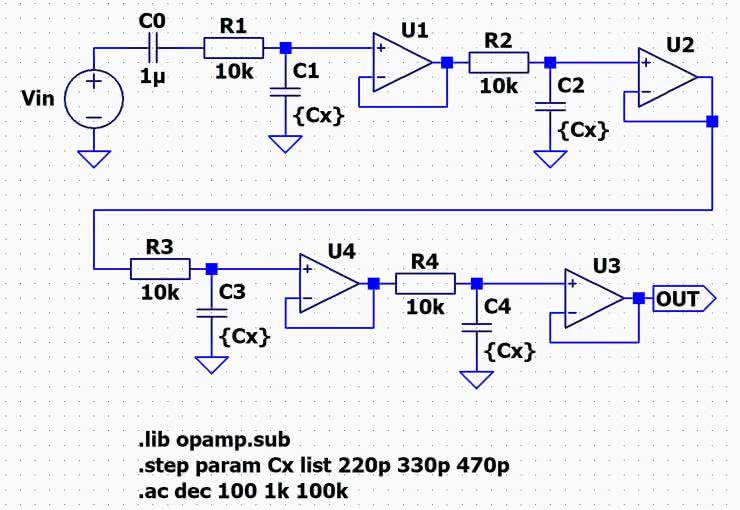
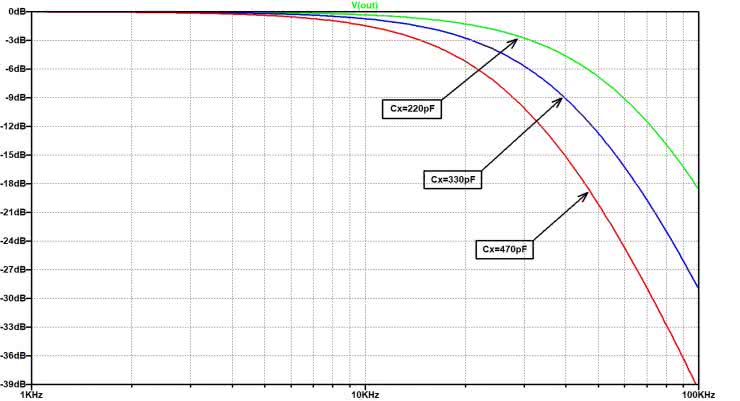
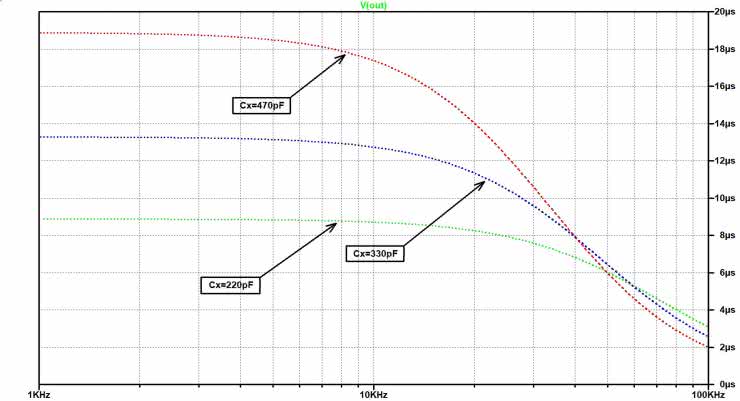
Analogowe układy filtrujące, realizujące zadania bloków: filtru antyaliasingowego oraz filtru rekonstrukcji C/A, pokazanych na rysunku 34a, zrealizowano wg tej samej prostej koncepcji czterostopniowego filtru RC. Poszczególne człony RC (pierwszego rzędu) zostały odseparowane wtórnikami opartymi na czterech wzmacniaczach operacyjnych, zawartych w strukturze układu MCP6004. Taka nieskomplikowana koncepcja filtrów pozwoliła na uzyskanie znacznej impedancji wejściowej w całym przetwarzanym pasmie częstotliwości, niskiej impedancji wyjściowej, niemal idealnie płaskiej charakterystyki przenoszenia w pełnym użytecznym paśmie oraz prawie stałe opóźnienie grupowe w tymże zakresie częstotliwości. Cechy te są bardzo korzystne z punktu widzenia pomiarowego przeznaczenia zaprojektowanych filtrów analogowych, a ich niezwykle prosta topologia dodatkowo istotnie ułatwia eksperymenty związane z korektą parametrów użytkowych filtrów, jednocześnie znacznie obniżając ich wrażliwość na rozrzut wartości zastosowanych elementów RC. Nie byłoby to możliwe w przypadku zastosowania filtrów kratowych, np. w topologii Sallen-Key czy z wielokrotnym sprzężeniem zwrotnym. Na rysunku 39 zaprezentowano schemat elektryczny prototypu przedmiotowych filtrów analogowych, użytych do wariantowej, małosygnałowej, zmiennoprądowej symulacji AC (z trzema różnymi wartościami pojemności Cx=220 pF, 330 pF i 470 pF), zrealizowanej w środowisku LTspice [5, 8].
Na podstawie analizy uzyskanych charakterystyk: częstotliwościowych (rysunek 40) i opóźnienia grupowego (rysunek 41) przyjęto arbitralnie pojemność Cx=330 pF, zapewniającą Fg filtrów równą 20 kHz (przy tłumieniu –3 dB) oraz monotoniczne opóźnienie grupowe, którego zmienność w zakresie pasma przenoszenia filtru nie przekraczała 10% wartości na początku tego pasma.
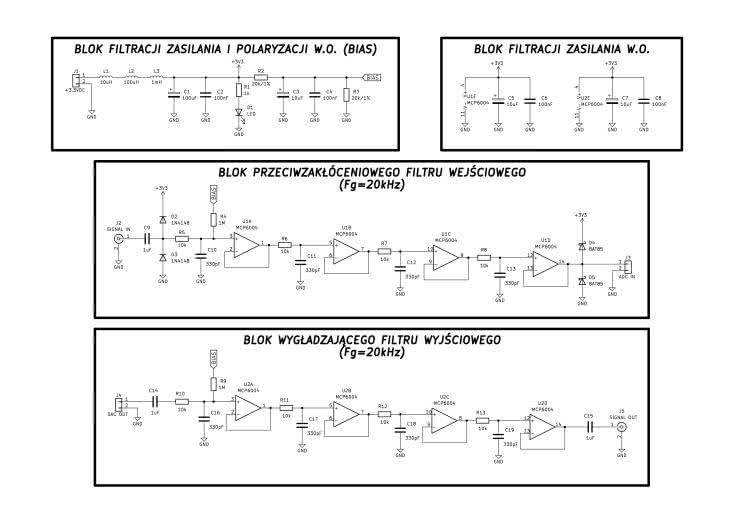
Należy w tym miejscu wyjaśnić, że chociaż podana koncepcja filtrów analogowych nie zapewnia ich wysokiej skuteczności w roli filtrów antyaliasingowych, to w przedmiotowym zastosowaniu (czysto pomiarowym) nie jest to powód do zmartwienia, bowiem z uwagi na wysterowanie układu z założenia silnym, czystym sygnałem sinusoidalnym w dozwolonym pasmie przenoszenia, ryzyko zjawiska aliasingu praktycznie nie występuje. Filtr wejściowy należy zatem traktować jako profilaktyczny filtr przeciwzakłóceniowy, natomiast filtr wyjściowy – jako układ wygładzający dla sygnału wyjściowego, odtworzony prostokątnymi próbkami przetworzonego sygnału testowego. Na rysunku 42 zaprezentowano schematy elektryczne fizycznych realizacji układów obu omawianych filtrów analogowych.
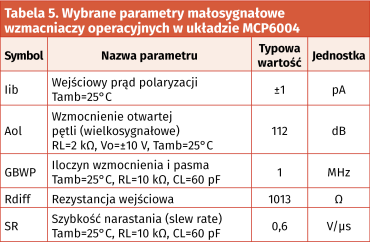
Zastosowano w nich dwa poczwórne wzmacniacze operacyjne typu MCP6004 (U1A..D oraz U2A..D; wybrane parametry małosygnałowe tych układów podano w tabeli 5).
Ogromną zaletą zastosowanych wzmacniaczy operacyjnych jest zdolność do pracy ich wejść i wyjść w trybie RRIO (rail-to-rail input/output) – i to także przy niskim napięciu zasilania Vdd=+3,3 V, którym jest natywnie zasilany mikrokontroler STM32L432KC modułu STM32-Nucleo. Dlatego celowo do zasilania układów U1 i U2 użyto właśnie tego napięcia. Zabieg ten miał na celu nie tyle uproszczenie konstrukcji bloku filtrów analogowych, co raczej zagwarantowanie, że wejście ADC mikrokontrolera nie zostanie przesterowane (co wiązałoby się z wysokim ryzykiem uszkodzenia MCU). Ostatecznie przeciwzakłóceniowy filtr wejściowy został uzupełniony o wstecznie spolaryzowane diody zabezpieczające D2 i D3 (2×1N4148) na wejściu oraz D4 i D5 (2×BAT85) na wyjściu (diody Schottky’ego na wejściu nie sprawdzały się z uwagi na dość znaczne i nieidentyczne prądy wsteczne, które istotnie zaburzały wartość napięcia BIAS, polaryzującego wejście wzmacniacza U1A). Napięcie BIAS, polaryzujące wejścia U1A i U2A, jest uzyskiwane wprost z dzielnika rezystancyjnego R2 i R3 (bez dodatkowego wtórnika), z uwagi na znikome wejściowe prądy polaryzacji użytych układów.
Elementy bierne L1...L3 oraz C1...C8 skutecznie separują napięcia zasilania Vdd i polaryzacji BIAS układów U1 i U2 od zasilania MCU, a dioda LED D1 z opornikiem R1 sygnalizuje obecność zasilania bloku filtrów. Fotografia 6 prezentuje przygotowaną płytkę testową – z wyróżnionymi na niej: zastosowanym modułem STM32-NUCLEO oraz blokiem filtrów analogowych.
Oprogramowanie
Jak wspomniano wcześniej, do projektowania obwodów filtrów analogowych współpracujących z MCU wykorzystano popularne, stabilne i sprawdzone środowisko LTspice [5, 8]. Z kolei oprogramowanie mikrokontrolera napisano w środowisku STM32CubeIDE [6] – m.in. z użyciem bibliotek HAL (ang. Hardware Abstraction Layer) [7].
Natomiast właściwe filtry cyfrowe DSP zaprojektowano z użyciem darmowego środowiska Octave (pakiet ‘signal’) [8], przeznaczonego do szeroko pojętego programowania matematycznego i inżynierskiego. Oprogramowanie Octave w znacznym zakresie zastosowań może zastępować w pełni profesjonalne, niezwykle zaawansowane i rozbudowane, komercyjne środowisko MATLAB, do którego to języka ma też bardzo podobną składnię.
Filtry cyfrowe FIR zostały zaimplementowane wg ram poniższego algorytmu:
- Projektowanie filtru FIR o zadanym typie, parametrach i jak najwyższym rzędzie Nord ≤ 28, zapewniającym poprawne wykonywanie obliczeń w pętli ze stałą częstotliwością próbkowania Fs=48 kHz (środowisko Octave, pakiet ‘signal’, funkcje: fir1() oraz freqz()),
- Jednorazowe zdefiniowanie w kodzie programu MCU współczynników filtru FIR oraz bufora – rejestru przesuwnego FIFO na pobrane próbki sygnału wejściowego (oba o długości Nord+1),
- Zainicjowanie w MCU bloków peryferiów GPIO, ADC oraz DAC i wyznaczenie składowej stałej na wejściu ADC (tzw. offset – do usunięcia z pobranych próbek w kolejnych krokach obliczeniowych).
- Wykonywanie w nieskończonej pętli następujących kroków:
- zlecenie ADC pobrania kolejnej próbki sygnału wejściowego,
- przesunięcie bufora – rejestru próbek FIFO o jedną próbkę, „gubiące” najstarszą próbkę na końcu rejestru i przygotowujące miejsce na wpis nowej danej na jego początku,
- odczyt nowego wyniku konwersji z ADC,
- przeliczenie wyjścia filtru FIR wg zależności (2) i schematu na rysunku 38,
- zapis wyliczonej wartości wyjścia filtru FIR do przetwornika DAC w MCU,
- powrót na początek nieskończonej pętli IV.
Projekty i analiza własności opracowanych filtrów FIR
Na potrzeby tej publikacji opracowano i przebadano cyfrowe odpowiedniki FIR wszystkich pięciu projektów amplifiltrów analogowych, prezentowanych w 2. i 3. odcinku naszego kursu (Filtry aktywne m.cz. typu Sallen-Key oraz Amplifiltry wąskopasmowe).
Do projektowania filtrów użyto wbudowanej funkcji programu Octave o nazwie fir1(). Jej zastosowanie jest bardzo proste – oprócz wymaganego rzędu projektowanego filtru należy jeszcze określić jego rodzaj (za pomocą jednego z parametrów – ciągów tekstowych: low, high, stop, pass, bandpass, DC-0 oraz DC-1). Oprócz tego należy jeszcze określić jeden lub dwa momenty znamienne (wyrażone częstotliwością znormalizowaną względem wartości Fs/2), w których oczekiwany jest środek obszaru przejścia (spadku lub wzrostu) częstotliwościowej charakterystyki przejściowej projektowanego filtru cyfrowego. Poprawnie sparametryzowana funkcja fir1() daje na wyjściu ciąg b(n) rzeczywistych współczynników filtru FIR, przy czym liczba tych współczynników jest zawsze o 1 większa od rzędu filtru Nord. Opcjonalne okno kształtowania charakterystyki można podać jako wektor w – także o długości Nord+1. Jeśli nie określono inaczej, używane jest okno Hamminga o stosownej długości. Przy zastosowaniu opcji noscale współczynniki filtru nie są normalizowane, jednak domyślnie filtr jest generowany w formie znormalizowanej – tak, aby odpowiedź amplitudowa dla środka pierwszego pasma przepustowego wynosiła 1. W opisywanych dalej projektach uzyskane za pomocą funkcji fir1() ciągi współczynników b(n) były dodatkowo mnożone przez liczbę 212 i zaokrąglane do najbliższej wartości całkowitej, co umożliwiło implementację w obliczeniach arytmetyki całkowitoliczbowej (z zasady znacznie szybszej od arytmetyki zmiennoprzecinkowej), z satysfakcjonującą dokładnością odwzorowania filtrów. Oczywiście rezultat uzyskany na wyjściu filtru FIR był ponownie skalowany „w dół” o tę samą wartość 212, której wybór pozwolił zamienić zwykle stosunkowo wolną operację dzielenia „x/(212)” na bardzo szybkie przesunięcie bitowe w prawo „x >> 12”. Na koniec warto zapamiętać to, że filtry typu high oraz notch wymagają podania jako parametru wejściowego funkcji fir1() parzystej wartości rzędu filtru Nord – jeśli sami o to nie zadbamy, to program zapewne automatycznie zwiększy Nord o jeden, co w przypadku krytycznie wysokiego wykorzystania czasu obliczeniowego pomiędzy pobraniem kolejnych próbek (z częstotliwością Fs) może doprowadzić do skrajnie nieprawidłowej pracy badanego układu filtracyjnego.
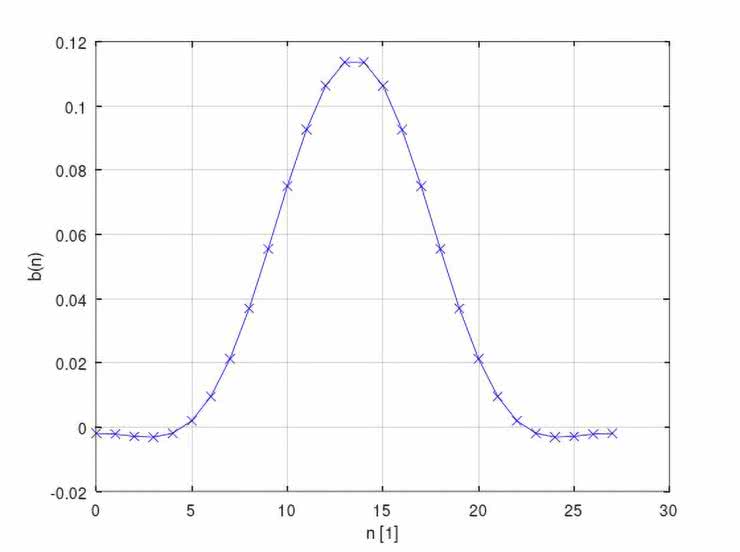
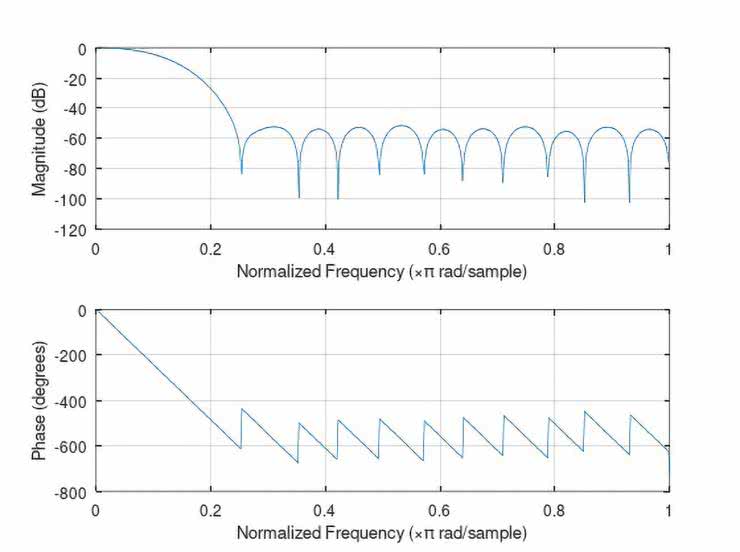
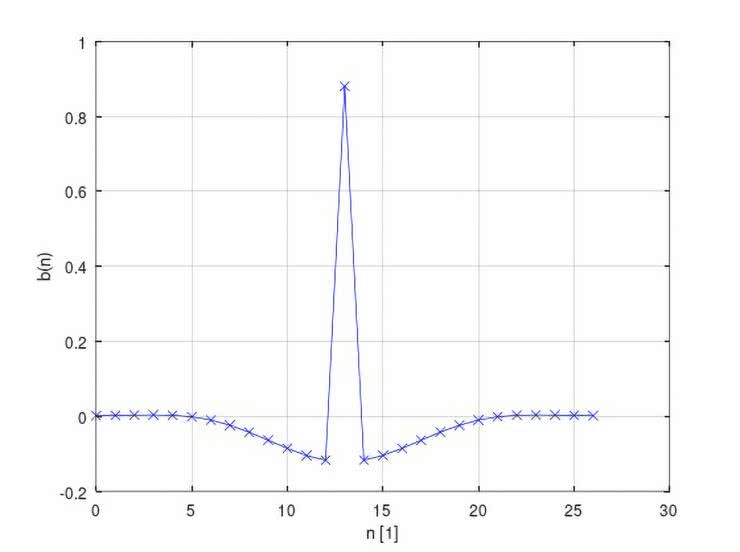
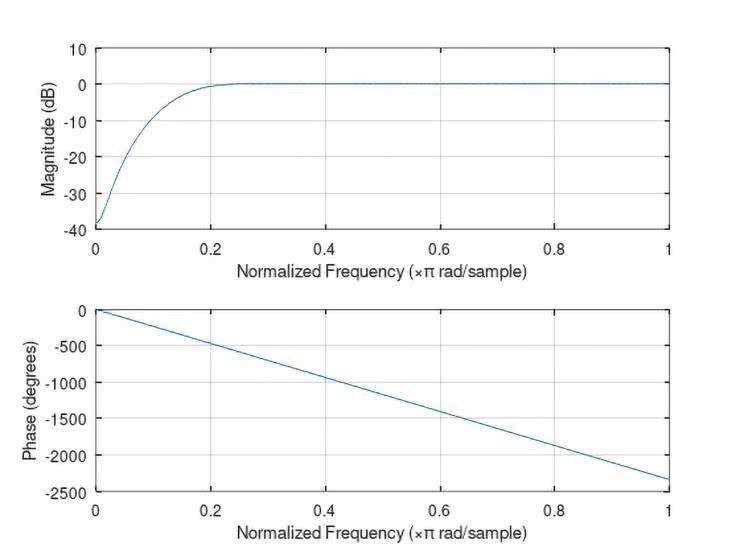
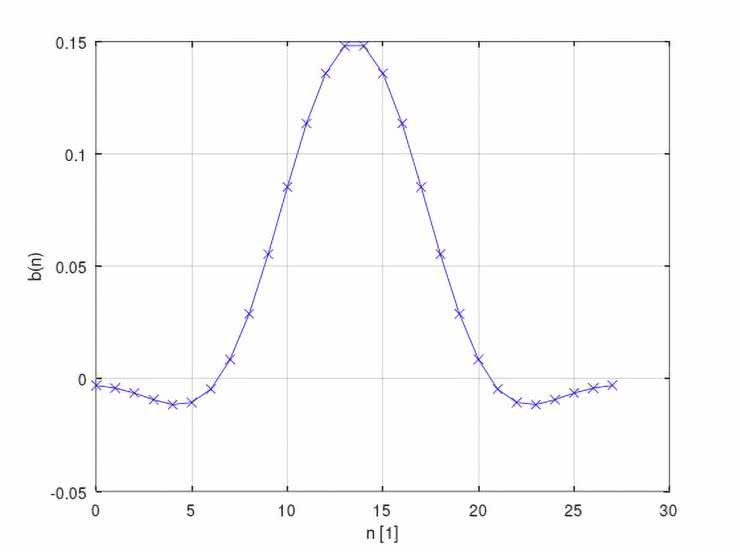
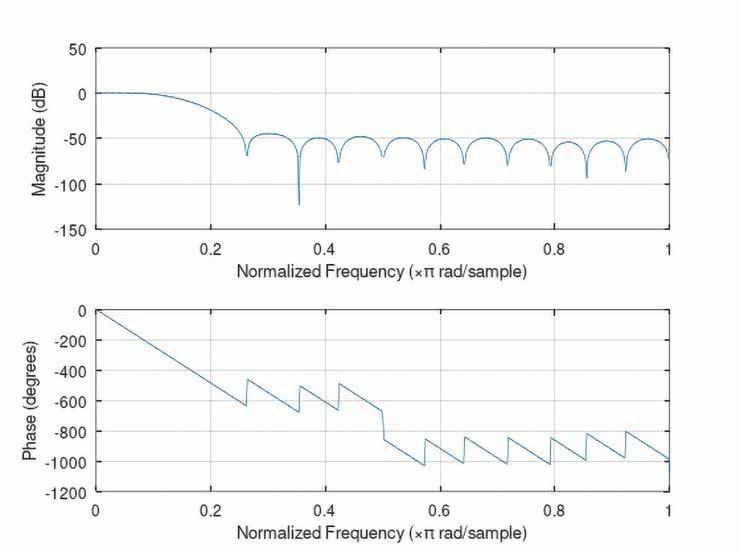
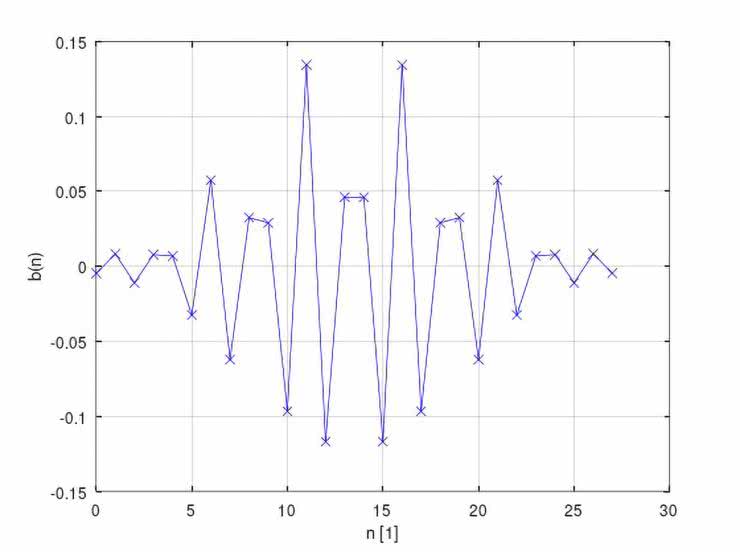
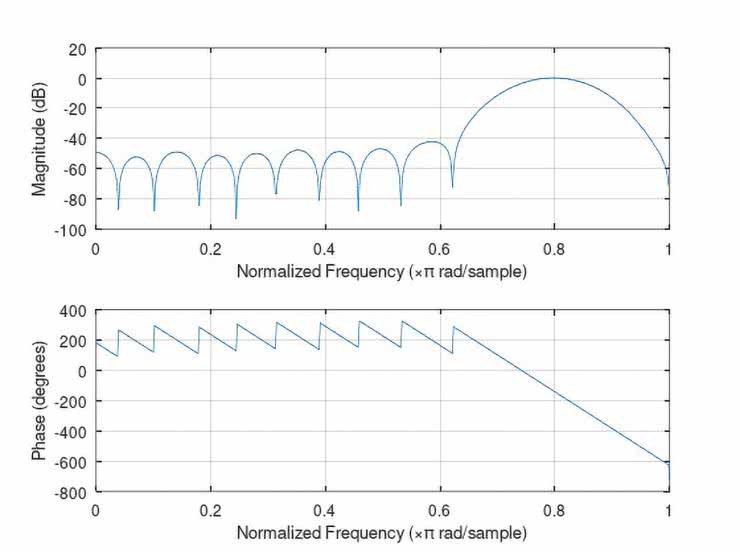
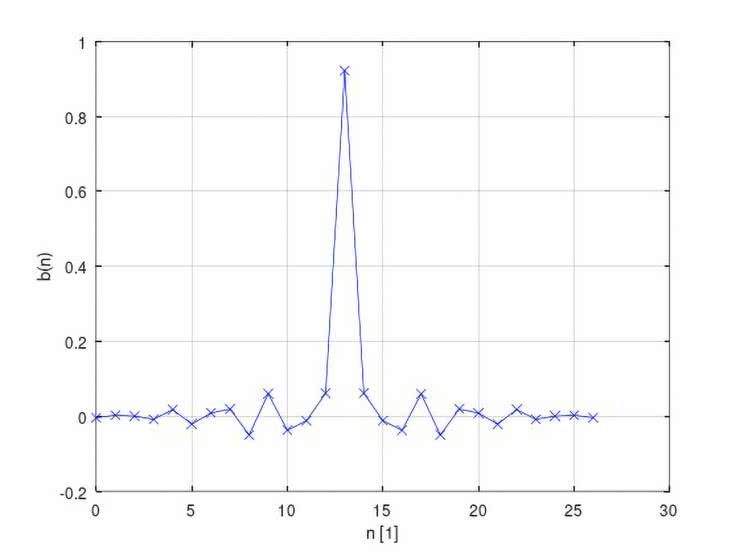
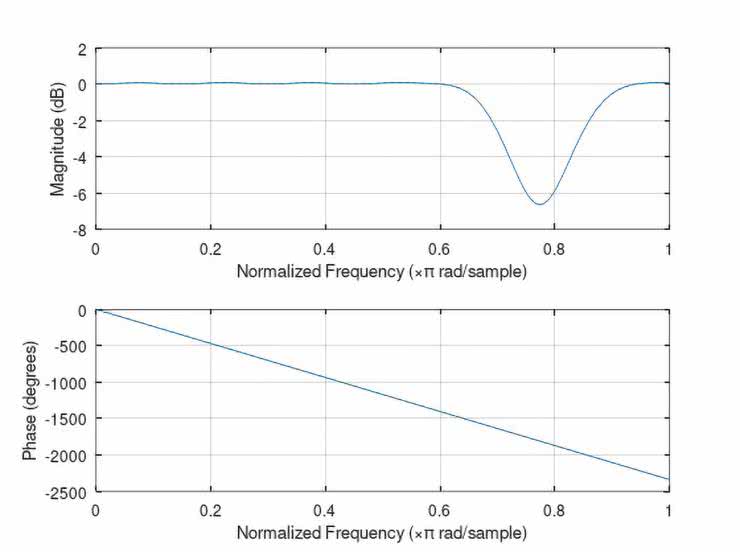
Na rysunkach 43...52 ujęto zestawy wykresów (po dwa na jeden filtr), obrazujących kolejno: przebieg współczynników b(n) danego filtru, a także jego wyliczone charakterystyki: amplitudową i fazową.
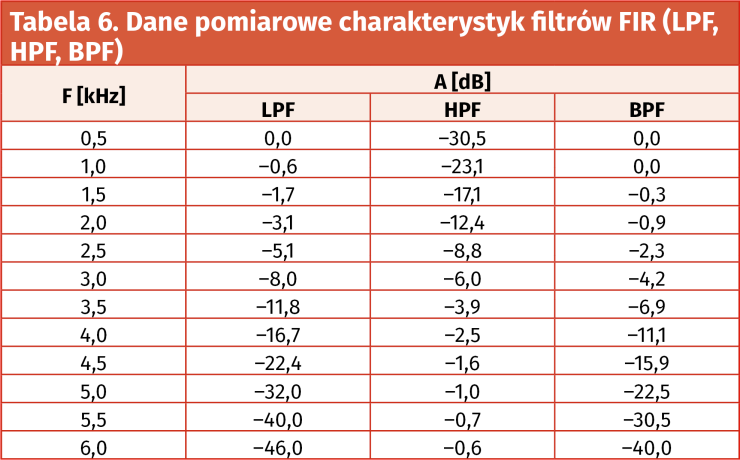
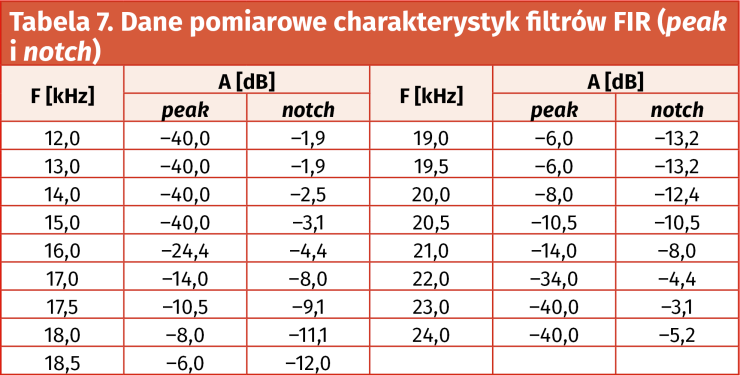
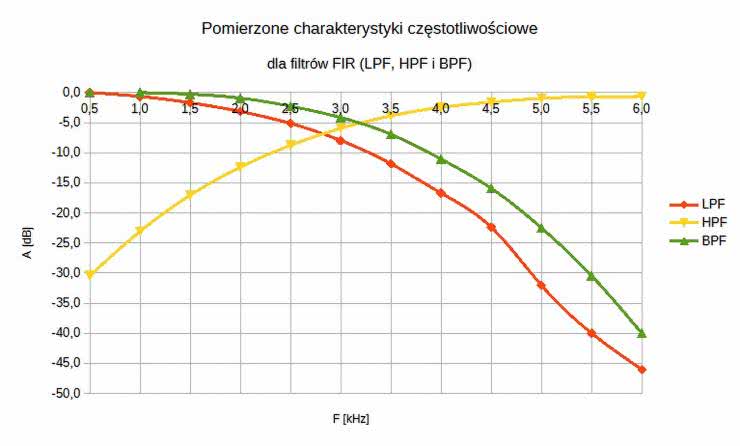
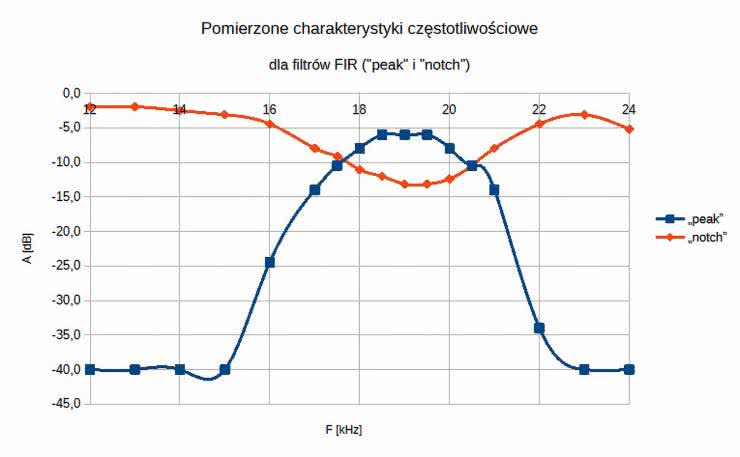
Natomiast pomierzone najistotniejsze fragmenty charakterystyk częstotliwościowych badanych filtrów ujęto w tabelach 6 i 7 (dane liczbowe) oraz na wykresach, na rysunkach 53 i 54. O ile zgodności wyliczonych i zmierzonych charakterystyk częstotliwościowych filtrów FIR typu LPF, HPF oraz BPF nie budzą większych zastrzeżeń (z dokładnością ograniczoną przez możliwości pomiaru bardzo małych napięć wyjściowych Uwy), o tyle już uzyskane charakterystyki filtrów cyfrowych (zwłaszcza peak i notch) zdecydowanie otwierają szerokie pole do dyskusji nad optymalizacją – zarówno samych rozwiązań projektowych, jak i obranych technik obliczeniowych i/lub pomiarowych.
Podsumowanie i wnioski
W artykule zaprezentowano minimalne podstawy teoretyczne, niezbędne do projektowania w technice DSP filtrów cyfrowych typu FIR, a także projekt względnie prostej platformy sprzętowej, niezbędnej do fizycznej implementacji opracowanych pięciu filtrów cyfrowych, które następnie przebadano symulacyjnie i pomiarowo. Rezultaty pomiarów nie we wszystkich przypadkach okazały się satysfakcjonujące, co jest solidnym uzasadnieniem do przeprowadzenia dalszych badań i optymalizacji w zakresie projektów i implementacji fizycznej omówionych filtrów cyfrowych. Do kierunków tych poszukiwań będą należały zapewne: wydłużenie projektowanych filtrów FIR na drodze redukcji nakładu obliczeniowego per jednostkowy element filtru, zastosowanie filtrów rekursywnych IIR oraz użycie dedykowanych bibliotek z rodziny CMSIS. Jako opcję można też rozważyć pewne obniżenie zastosowanej częstotliwości próbkowania Fs przy jednoczesnej optymalizacji właściwości analogowych (sprzętowych) filtrów: wejściowego i wyjściowego w opracowanym układzie pomiarowym. Otwartą kwestią pozostaje także możliwość dokładnego pomiaru bardzo małych napięć na wyjściu badanego układu (np. przy napięciu sinusoidalnym na wejściu badanego układu równym Uwe=1 Vp-p i tłumieniu filtru rzędu A=–60 dB powinniśmy być w stanie pomierzyć dokładnie parametry sinusoidy o napięciu wyjściowym rzędu Uwy=1 mVp-p). Wszystkie wymienione w podsumowaniu zagadnienia będą przedmiotem rozważań w kolejnych odcinkach niniejszego kursu.
Adam Sobczyk, EP
Literatura:
[1] Cyfrowe przetwarzanie sygnałów w telekomunikacji. Podstawy. Multimedia. Transmisja, Praca zbiorowa pod redakcją naukową: Tomasz P. Zieliński oraz Przemysław Korohoda i Roman Rumian, Wydawnictwo Naukowe PWN SA, Warszawa 2014, wydanie 1,
[2] Wprowadzenie do cyfrowego przetwarzania sygnałów, Richard G. Lyons, Wydawnictwa Komunikacji i Łączności sp. z o.o., Warszawa 1999, wydanie 1,
[3] STM32L432KB STM32L432KC. Datasheet, www.st.com, May 2018, DS11451, Rev. 4
[4] UM1956. User manual. STM32 Nucleo-32 boards (MB1180), November 2018, Rev. 5
[5] Zasoby dotyczące symulatora LTspice, https://tiny.pl/0-3cfvbb
[6] Zasoby dotyczące środowiska programistycznego STM32 CubeIDE, https://tiny.pl/mrnvy7vp
[7] UM1884. User manual. Description of STM32L4/L4+ HAL and low-layer drivers, www.st.com, September 2021, Rev. 9
[8] Signal processing tools, including filtering, windowing and display functions, https://tiny.pl/dnn6d5cg

 Zaloguj
Zaloguj