Przed lekturą niniejszego artykułu koniecznie przeczytaj odcinek 22, ponieważ dokładnie wytłumaczono w nim sposób działania algorytmu. A skoro nie musimy ponownie wyjaśniać tego zagadnienia, od razu przystąpimy do omawiania implementacji algorytmu sposobem kombinacyjnym.
Zasadnicza różnica między implementacją sekwencyjną i kombinacyjną jest taka, że układ kombinacyjny nie ma elementów pamięciowych tzn. przerzutników. Nie potrzebuje także sygnału zegarowego ani resetującego. Składa się tylko z bramek logicznych, multiplekserów, sumatorów i innych elementów kombinacyjnych, a stan jego wyjść zależy wyłącznie od obecnego stanu wejść. Po zmianie stanu wejść stan wyjść ustala się natychmiast po upływie pewnego czasu, zwanego czasem propagacji (więcej na ten temat pisaliśmy w odcinku 11, poświęconym statycznej analizie czasowej i maksymalnej częstotliwości zegara).
Moduł DoubleDabble w wersji kombinacyjnej
Przejdźmy do analizy kodu, pokazanego na listingu 1. Wejścia, wyjścia i parametry działają tak samo jak w poprzednim odcinku, z tą różnicą, że usunięte zostały wszystkie wejścia/wyjścia sterujące maszyną stanów, wejście zegarowe i reset. Z nich wszystkich pozostało tylko wejście Binary_i, na które dostarczamy liczbę zapisaną w formacie binarnym – oraz wyjście BCD_o, z którego odczytywać będziemy wynik w formacie BCD.
`default_nettype none
module DoubleDabble #(
parameter INPUT_BITS = 16,
parameter OUTPUT_DIGITS = 5,
parameter OUTPUT_BITS = OUTPUT_DIGITS * 4
)(
input wire [ INPUT_BITS-1:0] Binary_i,
output reg [OUTPUT_BITS-1:0] BCD_o
);
// Iteratory pętli for
integer i; // 1
integer j; // 2
// Blok kombinacyjny
always @(*) begin // 3
BCD_o = 0; // 4
// Dla każdego bitu na wejściu
for(i=0; i<INPUT_BITS; i=i+1) begin // 5
// Dla każdej cyfry na wyjściu
for(j=0; j<OUTPUT_BITS; j=j+4) begin // 6
// Jeżeli cyfra jest >= 5
if(BCD_o[j+:4] >= 4’d5) begin // 7
// To dodaj 3 do tej cyfry
BCD_o[j+:4] = BCD_o[j+:4] + 4’d3; // 8
end
end
// Przesuń bity w rejestrze
// i dodaj kolejny bit z wejścia danych Binary_i
BCD_o = {BCD_o[OUTPUT_BITS-2:0], // 9
Binary_i[(INPUT_BITS-1)-i]};
end
end
endmodule
`default_nettype wire
Listing 1. Kod pliku double_dabble.v
Parametr INPUT_BITS określa, ile bitów ma mieć wejście liczby binarnej. OUTPUT_DIGITS definiuje, ile cyfr BCD ma być na wyjściu, a OUTPUT_BITS ustala, ile bitów ma mieć to wyjście. Jeżeli w instancji modułu wspomniany parametr nie zostanie zdefiniowany, to ustawi się automatycznie jako liczba cyfr pomnożona przez 4. Czasem okaże się, że nie ma potrzeby, by używać dokładnie takiej liczby bitów – wówczas parametr ten można ustawić ręcznie. Przykładem opisanej sytuacji jest wejście 10-bitowe, na którym można ustawić liczbę od 0 do 1023, czyli cztery cyfry. W kodzie BCD zajmują 16 bitów, lecz pierwsza cyfra jest w stanie przyjmować wartość jedynie 0 lub 1. Zatem nie ma przeszkód, by skrócić ją jedynie do jednego bitu – i w takiej sytuacji wyjście może mieć jedynie 13 bitów.
W naszym module będziemy stosować dwie zagnieżdżone pętle for. Pierwsza z nich przeznaczona jest do wykonywania operacji na każdym bicie na wejściu Binary_i, a druga – na każdej cyfrze na wyjściu BCD_o. W języku Verilog iteratory pętli musimy utworzyć, zanim rozpocznie się pętla for. Robimy to w liniach 1 i 2, w których tworzymy zmienne typu integer o nazwach i oraz j (uwaga na przyzwyczajenia z C i C++, w Verilogu zmienna całkowita to integer, a nie int).
Moduł składa się tylko z jednego kombinacyjnego bloku always (linia 3). Rozpoznajemy ten fakt po liście czułości bloku – zamiast @(posedge Clock, negedge Reset), tym razem widzimy @(*), co oznacza, że blok ma wykonać jakąś operację zawsze wtedy, kiedy zmieni się dowolna zmienna w nim odczytywana.
Przypominam, że w blokach kombinacyjnych stosujemy przypisania blokujące = zamiast nieblokujących <=. Ponadto, jeżeli jakaś zmienna jest modyfikowana w wielu miejscach, to syntezator weźmie pod uwagę to przypisanie, które zostaje wykonane jako ostatnie. Zasada działania wygląda podobnie, jak w standardowych językach programowania.
Jedyną zmienną, na której będziemy pracować, jest BCD_o, stanowiąca jednocześnie wyjście modułu. W linii 4 nadajemy tej zmiennej wartość 0 (aby przypisać jakąś wartość początkową), a następnie będziemy ją modyfikować na różne sposoby.
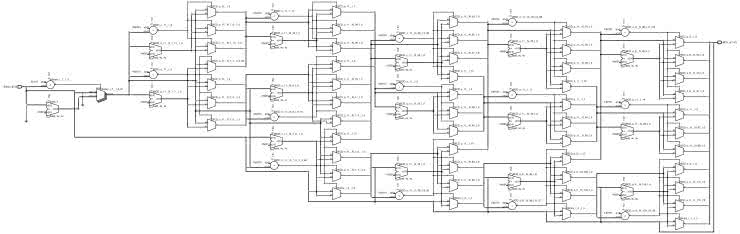
Kod algorytmu Double Dabble w wersji kombinacyjnej jest niezwykle zwarty. Składa się z zaledwie kilku linijek, przez co wygląda dość prosto, lecz może okazać się trudny do zrozumienia. Postaram się wytłumaczyć go w przystępny sposób. Zobaczmy rysunek 1. Jest to schemat wygenerowany automatycznie przez Netlist Analyser na podstawie kodu w języku Verilog, skonfigurowanego parametrami do obsługi wejścia 8-bitowego.
Widzimy na nim mnóstwo multiplekserów, sumatorów i komparatorów cyfrowych. W tej pajęczynie da się dostrzec pewne regularne wzorce, jak na przykład „ściany” multiplekserów, a także sumatory i komparatory cyfrowe występujące parami. Te elementy zostały utworzone w pętlach for. Pamiętać należy, że Verilog nie jest typowym językiem programowania, lecz językiem opisu sprzętu. Pętla for nie stanowi zbioru instrukcji, wykonywanych wielokrotnie przez procesor. Jest to raczej polecenie dla syntezatora, że ma utworzyć zbiór podobnie działających obiektów i umieścić je wszystkie w strukturze FPGA, a także wskazówka, że wszystkie z nich będą działać jednocześnie.
Pierwszą pętlę for rozpoczynamy w linii 5 i ma się ona wykonać tyle razy, ile bitów jest w zmiennej wejściowej. Wewnątrz niej znajduje się kolejna pętla, która ma wykonać się dla każdej liczby BCD na wyjściu (linia 6). Zwróć uwagę, że iterator pętli j po każdym obiegu jest zwiększany o 4, ponieważ cyfry BCD są zawsze 4-bitowe. W ten sposób przetwarzać będziemy liczbę wyjściową w 4-bitowych fragmentach.
W linii 7 sprawdzamy, czy cyfra wskazywana przez iterator pętli j jest większa lub równa 5. Jeżeli tak, to powiększamy tę cyfrę o 3 (linia 8), a jeżeli nie, to przekazujemy ją dalej bez zmian. Te dwie linie wygenerują nam trzy elementy logiczne:
- komparator cyfrowy, który na jednym wejściu ma liczbę 5, a na drugim cyfrę BCD,
- sumator, który na jednym wejściu ma stałą 3, a na drugim cyfrę BCD,
- multiplekser, który – w zależności od wyniku z komparatora – przekazuje dalej albo wynik sumatora, albo oryginalną (niezmienioną) liczbę BCD.
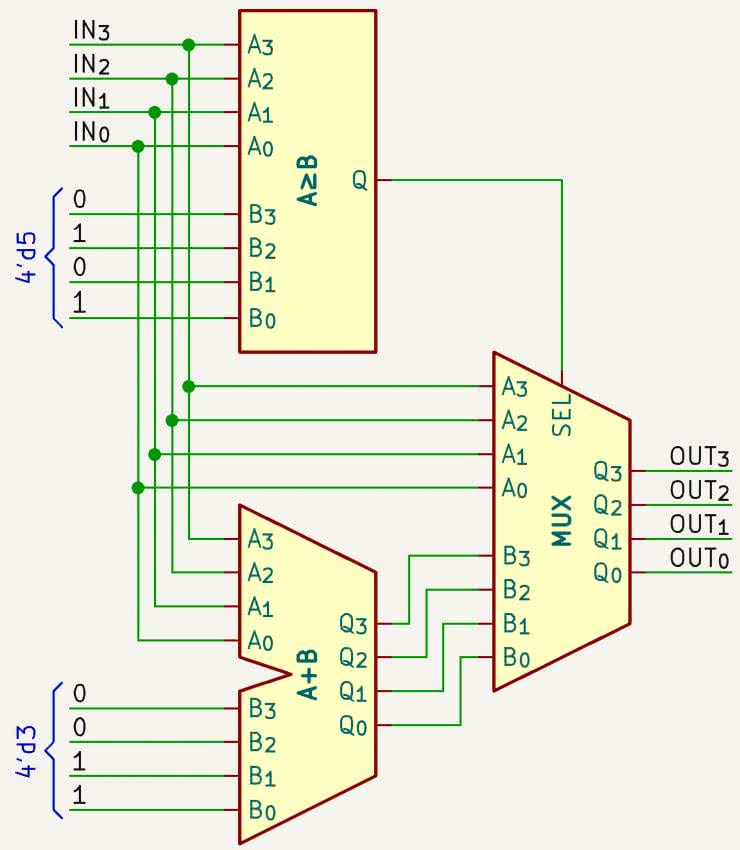
Schemat tego elementu „dodaj 3, jeżeli większe lub równe 5” pokazano na rysunku 2. Jest to podstawowa jednostka algorytmu Double Dabble w wersji kombinacyjnej. Stosując dwie pętle for, powielamy ten element, w zależności od liczby bitów na wejściu oraz liczby cyfr na wyjściu.
Zwróćmy uwagę, w jaki sposób wskazywane są bity w rejestrze BCD_o w liniach 7 i 8. Stosujemy tam zapis BCD_o[j+:4], gdzie j przyjmuje wartości 0, 4, 8, 12, itd. Operator x+:y powoduje selekcję zakresu bitów, zaczynając od x-tego bitu i wybierając y kolejnych bitów w górę. W naszym przykładzie będą to zakresy [3:0], [7:4], [11:8], [15:12], itd.
W linii 9 modyfikujemy rejestr BCD_o, używając wartości tego rejestru obliczonej w liniach powyżej, ale odpowiednio przesuwamy jego bity i dodajemy kolejne bity z wejścia Binary_i.
Testbench modułu DoubleDabble
Zgodnie ze zwyczajem praktykowanym w tym kursie, przed wgraniem bitstreamu do FPGA przetestujemy nowy moduł w symulatorze. Testbench (listing 2) jest bardzo podobny do tego, który opracowaliśmy w poprzednim odcinku. Omówimy tylko fragment kodu, jakim aktualny testbench różni się od swojego poprzednika (z odcinka o sekwencyjnym algorytmie Double Dabble).
// (...)
// Testuj wszystkie wartości od zera do maksimum
for(i=0; i<=MaxInput; i=i+1) begin // 1
@(posedge Clock); // 2
Binary <= i; // 3
Verify(Binary, BCD); // 4
end
// Testuj wszystkie wartości od maksimum do zera
for(i=MaxInput; i>=0; i=i-1) begin // 5
@(posedge Clock);
Binary <= i;
Verify(Binary, BCD);
end
// (...)
Listing 2. Fragment pliku double_dabble_tb.v
Przejdźmy od razu do pętli for w sekwencji testowej (linia 1). Zadaniem tej pętli jest podanie wszystkich możliwych liczb na wejście modułu, zaczynając od 0 i kończąc na najwyższej możliwej liczbie (wynika to z parametru INPUT_BITS, który – określając liczbę bitów wejścia – ustala jednocześnie, jaka może być maksymalna liczba na tym wejściu). Poniżej mamy pętlę działającą podobnie, ale w odwrotnym kierunku (linia 5).
W testbenchu modułu Double Dabble w wersji sekwencyjnej pętla była podzielona na trzy fazy – ustawialiśmy dane na wejściu wraz z sygnałem uruchamiającym konwersję, potem kasowaliśmy dane i zerowaliśmy sygnał uruchamiający, a ostatecznie czekaliśmy na sygnał zakończenia pracy, by przekazać wynik do tasku weryfikującego.
Tutaj sposób działania jest dużo prostszy, ponieważ moduł w wersji kombinacyjnej w symulatorze działa natychmiast (oczywiście można wprowadzić jakiś czas propagacji do symulowanego modułu, ale tym razem tego nie robimy). Z tego powodu po każdym zboczu sygnału zegarowego (linia 2) ustawiamy dane na wejściu modułu (linia 3), a następnie wywołujemy task weryfikacyjny (linia 4).
Skrypt służący do przeprowadzenia symulacji zaprezentowano na listingu 3. Jest on bardzo prosty z uwagi na fakt, że moduł Double Dabble nie zawiera żadnych modułów podrzędnych. Po przeprowadzeniu symulacji powinieneś zobaczyć komunikaty widoczne na listingu 4.
iverilog -o double_dabble.o ^
double_dabble.v ^
double_dabble_tb.v
vvp double_dabble.o
del double_dabble.o
Listing 3. Kod pliku double_dabble.bat
===== START =====
INPUT_BITS: 8
OUTPUT_BITS: 12
OUTPUT_DIGITS: 3
MaxInput: 255
Pass: 512
Fail: 0
====== END ======
double_dabble_tb.v:100: $finish called at 1025000 (1ns)
Listing 4. Log po symulacji
Plik VCD z wynikami symulacji otwórz w przeglądarce GTKWave i skonfiguruj ją tak, by uzyskać widok jak na rysunku 3. Zmienna Binary_i prezentowana jest w formacie dziesiętnym, natomiast w przypadku BCD_o należy wybrać format szesnastkowy.
Moduł top
Przetestujemy nowy moduł Double Dabble dokładnie w taki sam sposób, jak robiliśmy to w poprzednim odcinku. Dla przypomnienia: enkoderem obrotowym będziemy zwiększać lub zmniejszać stan licznika, liczącego w zakresie od 0 do 9999, a sam stan będzie pokazywany na wyświetlaczu w postaci szesnastkowej i dziesiętnej.
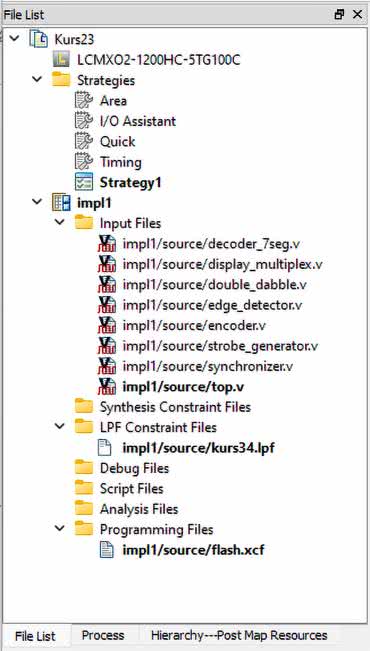
Utwórz nowy projekt i dodaj do niego pliki, które wskazano na rysunku 4. Wszystkie widoczne pliki, z wyjątkiem oczywiście pliku top.v, były już omawiane w kursie i znajdziesz je w repozytorium autora kursu na GitHubie [link 1].
Kod modułu top pokazano na listingu 5 – jest on bardzo podobny do omawianego w poprzednim odcinku. Różnica polega na tym, że modułu DoubleDabble nie musimy uruchamiać w kolejnym cyklu po zmianie stanu licznika. Nie potrzebujemy więc dodatkowego opóźniacza.
`default_nettype none
module top #(
parameter CLOCK_HZ = 25_000_000
)(
input wire Clock, // Pin 20
input wire Reset, // Pin 17
input wire EncoderA_i, // Pin 68
input wire EncoderB_i, // Pin 67
output wire [7:0] Cathodes_o, // Pin 40 41 42 43 45 47 51 52
output wire [7:0] Segments_o // Pin 39 38 37 36 35 34 30 29
);
// Zmienna na potrzeby enkodera obrotowego
wire Increment;
wire Decrement;
// Instancja modułu enkodera obrotowego
Encoder Encoder_inst(
.Clock(Clock),
.Reset(Reset),
.AsyncA_i(EncoderA_i),
.AsyncB_i(EncoderB_i),
.AsyncS_i(1’b1),
.Increment_o(Increment),
.Decrement_o(Decrement),
.ButtonPress_o(),
.ButtonRelease_o(),
.ButtonState_o()
);
// Licznik liczący w górę/dół w zakresie 0...9999 (dziesiętnie)
reg [15:0] Counter; // 1
// Logika licznika
always @(posedge Clock, negedge Reset) begin
if(!Reset) begin
Counter <= 0;
end else if(Increment) begin
if(Counter == 16’d9999)
Counter <= 16’d0;
else
Counter <= Counter + 1’b1;
end else if(Decrement) begin
if(Counter == 16’d0)
Counter <= 16’d9999;
else
Counter <= Counter – 1’b1;
end
end
// Zmienna do przekazywania wyniku z modułu Double Dabble
// do modułu wyświetlacza
wire [15:0] Decimal;
// Instancja modułu konwertera BIN/BCD
DoubleDabble #(
.INPUT_BITS(16),
.OUTPUT_DIGITS(4)
) DoubleDabble_inst(
.Binary_i(Counter), // 2
.BCD_o(Decimal) // 3
);
// Instancja modułu 8-cyfrowego wyświetlacza 7-segmentowego
DisplayMultiplex #(
.CLOCK_HZ(CLOCK_HZ),
.SWITCH_PERIOD_US(1000),
.DIGITS(8)
) DisplayMultiplex_inst(
.Clock(Clock),
.Reset(Reset),
.Data_i({Decimal, Counter}), // 4
.DecimalPoints_i(8’b00010000),
.Cathodes_o(Cathodes_o),
.Segments_o(Segments_o),
.SwitchCathode_o()
);
endmodule
`default_nettype wire
Listing. 5. Kod pliku top.v
Licznik Counter (linia 1) jest połączony bezpośrednio z wejściem Binary_i modułu DoubleDabble (linia 2) oraz wejściem Data_i modułu wyświetlacza DisplayMultiplex (linia 4). Tak samo wyjście BCD_o z DoubleDabble (linia 3) jest doprowadzone prosto do wejścia Data_i wyświetlacza (linia 4). Kod wydaje się na tyle prosty, że nie wymaga komentarza.
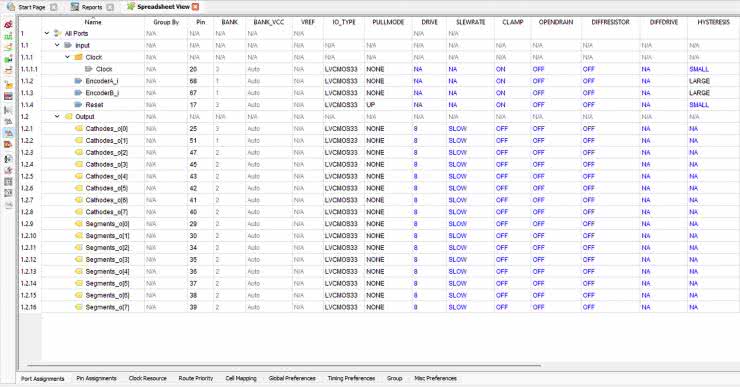
Po przeprowadzonej syntezie otwórz narzędzie Spreadsheet i skonfiguruj piny układu FPGA w taki sposób, jak to pokazano na rysunku 5.
Generujemy bitstream, wgrywamy do FPGA na płytce MachXO2 Mega umieszczonej w User Interface Board, kręcimy enkoderem i voilà! Układ działa dokładnie tak samo, jak w poprzednim odcinku.
Porównanie implementacji sekwencyjnej oraz kombinacyjnej
Utworzyliśmy dwa moduły realizujące algorytm Double Dabble, które dają dokładnie taki sam wynik, jednak uzyskują go w zupełnie inny sposób. Czas zastanowić się nad zaletami i wadami obu rozwiązań.
Wersja kombinacyjna umożliwia uzyskanie wyniku w tym samym cyklu zegarowym, w którym zostały podane dane na wejściu. Wersja sekwencyjna ma maszynę stanów, która dla każdego bitu na wejściu wykonuje dwie operacje – czyli dla wejścia o długości 8 bitów maszyna potrzebuje 16 taktów zegarowych plus jeden kolejny takt na skopiowanie danych.
Można odnieść wrażenie, że wersja kombinacyjna działa szybciej, bo uzyskujemy wynik w jednym takcie zegarowym. Jest to bardzo pozorne. Implementacja kombinacyjna tworzy nam cały łańcuch różnych elementów kombinacyjnych, których czas propagacji jest oczywiście niezerowy. Im więcej bitów na wejściu, tym więcej elementów kombinacyjnych i tym dłuższy czas propagacji. W rezultacie trzeba zastosować odpowiednio niską częstotliwość sygnału zegarowego, aby ogromny blok kombinacyjny zdążył przetworzyć dane (jeżeli chcesz lepiej zrozumieć ten problem, zachęcam do lektury 11 odcinka kursu na temat statycznej analizy czasowej).
Implementacja sekwencyjna co prawda wykonuje się w ciągu wielu taktów zegarowych, lecz częstotliwość zegara może być dużo wyższa, ponieważ takie rozwiązanie nie zawiera wielkich bloków kombinacyjnych.
Drugim istotnym aspektem do porównania jest zapotrzebowanie na zasoby logiczne w strukturze FPGA. Mnóstwo elementów kombinacyjnych zajmuje oczywiście dużo zasobów. Z drugiej jednak strony wersja sekwencyjna korzysta z maszyny stanów i wielu rejestrów, które również zajmują jakieś zasoby. Która wersja jest lepsza?
Aby odpowiedzieć na to pytanie, przeprowadziłem syntezę oraz statyczną analizę czasową obu wersji. Każdą implementację testowałem dla różnej szerokości wejścia danych, zaczynając od danej 1-bitowej, a kończąc na liczbie 32-bitowej, która dziesiętnie reprezentowana jest przez liczbę 10-cyfrową.
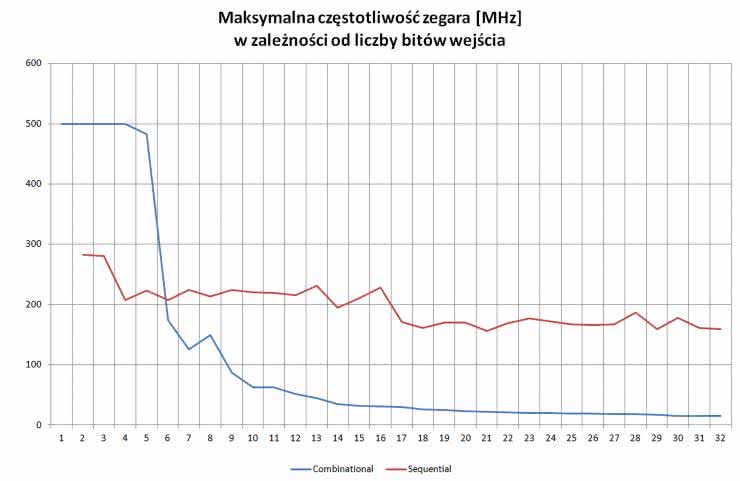
Zobaczmy rysunek 6. Na osi poziomej mamy liczbę bitów wejścia, a na pionowej – maksymalną częstotliwość zegara, jaka jest możliwa do uzyskania. Dla małej liczby bitów implementacja kombinacyjna okazuje się zdecydowanie lepsza niż sekwencyjna. Jednak maksymalna częstotliwość bardzo szybko maleje wraz ze wzrostem liczby bitów na wejściu. Już przy 6 bitach obie implementacje zrównują się, a powyżej 9 bitów częstotliwość spada poniżej 100 MHz. Moduł konwertujący liczbę 32-bitową może pracować z częstotliwością zaledwie 15 MHz. W tym przypadku implementacja sekwencyjna wypada zdecydowanie lepiej.
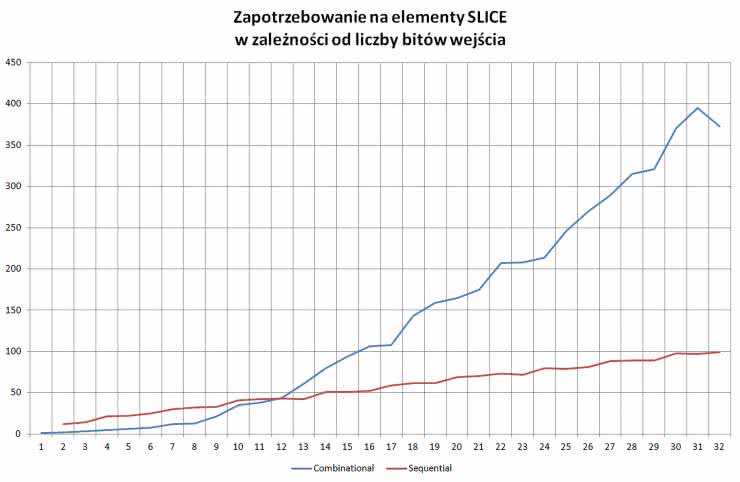
Zobaczmy, jak wygląda zapotrzebowanie na zasoby logiczne. Wykres na rysunku 7 pokazuje, ile elementów SLICE jest potrzebnych w zależności od liczby bitów zmiennej wejściowej. Jeżeli zmienna ma poniżej 12 bitów, lepiej wypada implementacja kombinacyjna, a powyżej – sekwencyjna. Widzimy, że – dla dużych liczb – moduł Double Dabble w wersji kombinacyjnej staje się niesamowicie zasobożerny.
Podsumowując, jeżeli chcemy konwertować liczbę 6-bitową lub mniejszą, to optymalnym wyborem jest implementacja kombinacyjna. Jeżeli nasza zmienna jest 12-bitowa lub większa – lepszym wyborem będzie implementacja sekwencyjna. W zakresie od 6 do 12 bitów obie wersje okazują się dobre. Jeżeli zależy nam na szybkim zegarze, należy wybrać wersję sekwencyjną, a jeżeli chcemy oszczędzać zasoby – optymalna będzie wersja kombinacyjna.
W następnym odcinku będziemy ćwiczyć w praktyce dotychczas opracowane moduły i zbudujemy miernik częstotliwości.
Dominik Bieczyński
leonow32@gmail.com

 Zaloguj
Zaloguj