Kurs FPGA Lattice (22). Sekwencyjny algorytm Double Dabble

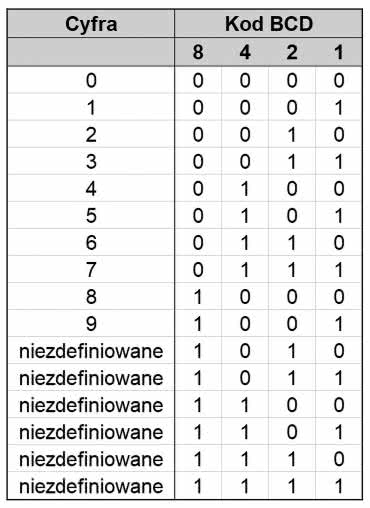
Najwygodniejszym sposobem na przekonwertowanie liczby zapisanej binarnie na format dziesiętny jest użycie kodu BCD (binary coded decimal). Każdą cyfrę dziesiętną zapisujemy jako 4-bitową liczbę binarną. Cztery bity dają możliwość utworzenia 16 kombinacji, ale w kodzie BCD stosujemy tylko kombinacje od 0 do 9, a pozostałe są nieużywane. Zobacz rysunek 1.

Rysunek 1. Kod BCD

Przykładowo: liczba dziesiętna 1234 zapisana w kodzie BCD będzie mieć 16 bitów i przyjmie postać 0001_0010_0011_0100. W kodzie binarnym byłoby to 100_1101_0010, czyli 11 bitów. Widzimy więc, że kod BCD nie jest optymalny, jeśli chodzi o zużycie zasobów, jednak pozwala w dość łatwy sposób operować na liczbach dziesiętnych.

Jak działa algorytm Double Dabble?

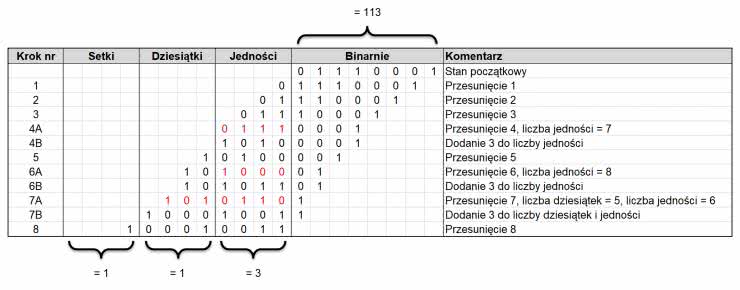
Najprościej będzie to wytłumaczyć na przykładzie. Zobacz rysunek 2. Chcemy przekształcić 8-bitową liczbę 113 na kod BCD. Jej binarna reprezentacja to 0b01110001. Umieszczamy ją w tabeli w kolumnie „Binarnie” i jest to stan początkowy algorytmu. Liczba ta jest 3-cyfrowa, zatem musimy przygotować trzy kolumny w tabeli – dla cyfr setek, dziesiątek i jedności – a każda z nich będzie miała 4 bity. Z tych kolumn odczytamy wynik w kodzie BCD.

Rysunek 2. Opis algorytmu Double Dabble krok po kroku

W celu zwiększenia czytelności, w tabeli pominąłem wszystkie bity, które są nieistotne. We wszystkich pustych komórkach należy wpisać zero.

Algorytm Double Dabble polega na wykonywaniu w pętli dwóch operacji. Pierwszą z nich jest przesunięcie wszystkich rejestrów o jeden bit w lewo. Takie przesuwanie liczb binarnych jest równoznaczne z pomnożeniem przez 2 – stąd angielska nazwa double. Następnie sprawdzamy każdą z cyfr. Jeżeli jest większa lub równa 5, to dodajemy do niej 3 – jest to faza dabble. Przesunięć musi być tyle, ile bitów ma liczba na wejściu.

Zobaczmy, jak to działa:

• W kroku 1 przesuwamy w lewo liczbę, którą mieliśmy na wejściu. Cyfry setek, dziesiątek i jedności wciąż są zerami.
• Przechodzimy do kroku 2. Ponownie przesuwamy wszystkie rejestry. Cyfra jedności stała się jedynką. Jest to mniej niż 5, więc idziemy dalej.
• Następnie, w kroku 3, po raz kolejny przesuwamy wszystko w lewo. Cyfra jedności to 0b0011, czyli dziesiętnie 3, a więc wciąż mniej niż 5.
• W kroku 4A ponownie przesuwamy rejestry. Okazuje się, że po przesunięciu cyfra jedności jest równa 0b0111 (zaznaczone na czerwono), czyli dziesiętnie 7. Zatem w kroku 4B musimy dodać do niej 3, co w rezultacie daje 10, czyli binarnie 0b1010.
• W kroku 5 ponownie przesuwamy. Wszystkie cyfry są mniejsze od 5.
• Podczas kroku 6A przesuwamy i sprawdzamy. Okazuje się, że cyfra jedności to 0b1000, czyli dziesiętnie 8. Zatem w kroku 6B dodajemy 3 i dostajemy 11, czyli binarnie 0b1011.
• Następnie znów przesuwamy wszystkie rejestry w kroku 7A. Sprawdzamy wszystkie cyfry. Okazuje się, że jednocześnie cyfra dziesiątek i jedności są większe lub równe 5. Zatem w kroku 7B do obu tych cyfr dodajemy 3. Dzieje się to w tej samej chwili.
• Krok 8 to ósme i ostatnie przesunięcie, ponieważ liczba na wejściu była 8-bitowa. Algorytm kończy pracę i możemy odczytać wynik. Cyfra setek w kodzie BCD to 0b0001, dziesiątek 0b0001, a jedności 0b0011, co daje nam liczbę 113 zapisaną w BCD.

Dochodzimy do wniosku, że dwa elementy sprzętowe, które potrzebne są do realizacji algorytmu Double Dabble w FPGA, to rejestr przesuwający, sumatory dla każdej cyfry i trochę prostych elementów logicznych, sklejających to wszystko w jedną całość (tak zwane glue logic).

Moduł Double Dabble w wersji sekwencyjnej

Moduł realizujący algorytm Double Dabble w wersji sekwencyjnej zaprezentowano na listingu 1.

Zacznijmy od omówienia parametrów, wejść i wyjść tego modułu:

• INPUT_BITS – ile bitów ma zmienna wejściowa,
• OUTPUT_DIGITS – ile cyfr ma mieć wynik,
• OUTPUT_BITS – ile bitów ma mieć wyjście; ten parametr ustawia się automatycznie w wyniku pomnożenia parametru OUTPUT_DIGITS przez 4.

Moduł wyposażony jest w następujące porty wejścia i wyjścia (Clock i Reset nie omawiamy, bo działają tak, jak we wszystkich dotychczas omawianych modułach):

• Binary_i – wejście danych w formacie binarnym,
• BCD_o – wyjście danych w formacie BCD,
• Start_i – wejście informujące moduł o żądaniu rozpoczęcia pracy; aby uruchomić moduł należy ustawić to wejście w stan wysoki na jeden takt zegarowy,
• Busy_o – stan wysoki na tym wyjściu informuje, że moduł jest w trakcie pracy,
• Done_o – wyjście informujące (poprzez ustawienie stanu wysokiego na jeden takt zegarowy), że moduł zakończył pracę, a wynik jest dostępny do odczytu na wyjściu BCD_o.

Ogólnie rzecz biorąc, moduł musi zawierać maszynę stanów, która będzie naprzemiennie wykonywać operacje double i dabble. Muszą one zostać wykonane tyle razy, ile jest bitów w zmiennej wejściowej, zatem potrzebujemy także licznika.

Przejdźmy do deklaracji zmiennych, używanych w module. W linii 1 tworzymy iterator pętli for (zwyczajowo nazywany i) będący zmienną typu integer. Następnie, w linii 2, mamy rejestr Binary, którego celem jest wykonanie kopii wejścia Binary_i. Taka potrzeba wiąże się z faktem, że stan wejścia może zmienić się podczas pracy, co skutkowałoby nieprawidłowym wynikiem. Aby temu zapobiec, musimy wykonać kopię danych wejściowych w dedykowanym rejestrze. Potrzebujemy jeszcze jednego rejestru, o nazwie BCD (linia 3). Posłuży on jako rejestr roboczy, w którym będziemy przesuwać bity, a kiedy moduł zakończy pracę, wówczas jego zawartość zostanie skopiowana do BCD_o.

Kluczową zmienną pozostaje rejestr maszyny stanów State, utworzony w linii 4. Maszyna ma tylko dwa stany, więc jest to rejestr 1-bitowy. Stany nazywamy za pomocą parametrów lokalnych DOUBLE i DABBLE w dwóch kolejnych liniach.

Następnie trzeba przygotować licznik, który będzie odliczał przesunięcia bitów. Musimy uwzględnić tyle przesunięć, ile jest bitów w zmiennej wejściowej (co określone zostało parametrem INPUT_BITS). Wygodnie będzie liczyć od maksymalnej wartości do zera – takie podejście jest optymalne z uwagi na wykorzystanie zasobów. Aby sprawdzić, czy stan licznika jest większy od zera, wystarczy nam bramka OR, sprawdzająca stan wszystkich jego bitów. Wyjście takiej bramki znajduje się w stanie niskim tylko wtedy, kiedy wszystkie jej wejścia również są w stanie niskim.

Jako pomoc przyda się nam zmienna przechowująca maksymalną wartość licznika. Tworzymy zatem parametr lokalny MAX_VALUE, do którego wpisujemy liczbę bitów wejścia pomniejszoną o jeden – jeżeli wejście jest 8-bitowe, to licznik będzie liczył od 7 do 0 (linia 5). Następnie musimy określić, ilu bitów potrzebuje licznik, aby „pomieścić” wartość maksymalną. W tym celu posługujemy się funkcją $clog2(x), która oblicza logarytm naturalny przy podstawie 2 z x – tą metodą tworzymy parametr lokalny WIDTH (linia 6). Jeżeli nie wiesz, dlaczego argument funkcji został powiększony o 1, zajrzyj do 6 odcinka kursu (EP 04/2023), w którym funkcja $clog2() została szczegółowo omówiona na przykładach. Finalnie, tworzymy właściwy licznik Counter o odpowiedniej liczbie bitów w linii 7.

Przechodzimy wreszcie do sekwencyjnego bloku always w linii 8, reagującego – jak zwykle – na rosnące zbocze sygnału zegarowego lub opadające zbocze sygnału resetującego. Kiedy Reset jest w stanie niskim, wówczas zerujemy wszystkie zmienne typu reg (linia 9).

Blok always wykonuje różne operacje w zależności od tego, czy w stanie wysokim znajdują się sygnały Start_i, Busy_o lub Done_o. Przejdźmy do linii 10 – sprawdzamy w niej stan wejścia Start_i, które jest żądaniem rozpoczęcia pracy. W takiej sytuacji ustawiamy wszystkie zmienne, by w kolejnym takcie wykonywać właściwą pracę modułu, a w szczególności kopiujemy wartość z wejścia Binary_i do rejestru Binary, ustawiamy zmienną Busy_o w stan wysoki, wartość licznika na maksymalną, a rejestr stanu maszyny State na DOUBLE, ponieważ ta operacja ma się wykonać w następnym takcie zegara.

Kiedy moduł jest w trakcie wykonywania pracy, tzn. kiedy zmienna Busy_o znajduje się w stanie wysokim (linia 11), wykonujemy różne działania w zależności od stanu zmiennej State (linia 12). Kiedy jest ona równa DOUBLE, czyli 1’b0, przesuwamy bity w rejestrach BCD i Binary oraz ustawiamy State na DABBLE (linia 13).

W stanie DABBLE (linia 14) musimy sprawdzić, czy któraś z cyfr BCD jest większa lub równa 5 – i jeżeli tak, to dodajemy do niej 3. Najprościej byłoby wykonać tę procedurę w poniższy sposób:

…i tak dalej, dla każdej cyfry. Moduł jest napisany w taki sposób, by umożliwić jego parametryzację i obsługę dowolnie długich liczb. Z tego powodu musimy przejść na nieco wyższy poziom abstrakcji i sprawdzać każdą cyfrę w pętli for.

Rozwiązanie to pokazano w linii 15. Iteratorem pętli for jest zmienna i typu integer, którą początkowo ustawiamy na 3 i w każdym obiegu pętli zwiększamy o 4. W ten sposób dostaniemy liczby 3, 7, 11, itd, które są indeksami najstarszych bitów w każdej z liczb BCD.

Aby wybrać poszczególne bity ze zmiennej wielobitowej, najczęściej stosujemy operator [MSB:LSB] – podajemy w nim indeks najstarszego oraz najmłodszego bitu, które chcemy odczytać lub zapisać. W tym przypadku musimy posłużyć się operatorem [MSB-:RANGE] i wskazać w nim: indeks najstarszego bitu oraz ile bitów w dół nas interesuje. Wszystkie cyfry BCD są 4-bitowe, zatem posłużymy się konstrukcją [i-:4], gdzie i jest iteratorem pętli for opisanym wyżej. W ten sposób sprawdzamy, czy każda z cyfr BCD jest większa lub równa 5 (linia 16) i jeżeli tak, to tę liczbę inkrementujemy o 3 (linia 17).

Jednocześnie, w tym samym takcie zegarowym, wykonujemy kilka innych operacji. Sprawdzamy, czy stan licznika Counter jest większy od zera (linia 18) – jeżeli tak, to zmniejszamy go o 1, a jeżeli nie – to znaczy, że przetworzyliśmy już wszystkie bity. Zatem zmienną Busy_o zerujemy, Done_o ustawiamy w stan wysoki i kopiujemy stan rejestru roboczego BCD na wyjście BCD_o.

Niezależnie od wszystkiego, zmieniamy stan rejestru maszyny stanów na DOUBLE (linia 20). Gdy algorytm zakończy pracę, działanie takie właściwie nie ma sensu, ale stwierdziłem, że również w niczym nie przeszkadza, a znacznie ułatwiło napisanie kodu.

Przechodzimy do ostatniego warunku w bloku always w linii 21. Jeżeli Done_o jest w stanie wysokim, to zerujemy tę zmienną.

Testbench modułu Double Dabble

Zgodnie z naszym zwyczajem opracujemy testbench, by przeprowadzić symulację nowego modułu. Jednak tym razem dodamy ciekawą funkcjonalność – testbench automatycznie przetestuje, czy moduł działa prawidłowo.

W przypadku konwersji liczby z formatu binarnego na BCD mamy stosunkowo proste zadanie, ponieważ moduł konwertera posiada tylko jedno wejście danych Binary_i (pozostałe wejścia istnieją w gruncie rzeczy tylko po to, by wykonanie algorytmu było możliwe) – i jedno wyjście danych BCD_o. Dzięki temu zyskujemy możliwość przetestowania wszystkich kombinacji – wystarczy tylko, by w pętli wrzucać do modułu wszystkie liczby od zera do maksimum. Weryfikacja polegać będzie na porównaniu odpowiedzi testowanego modułu z odpowiedzią obliczoną przez testbench podczas symulacji.

Przejdźmy do omówienia kodu testbencha, który pokazano na listingu 2.

Tym razem testbench rozpoczniemy od kilku parametrów, dzięki czemu będziemy mogli łatwo i szybko zmieniać konfigurację testowanego modułu. W linii 1 ustawiamy parametr INPUT_BITS informujący o tym, ile bitów ma mieć liczba w formacie binarnym. W linii 2, za pomocą parametru OUTPUT_DIGITS ustawiamy, ile cyfr ma mieć liczba wyjściowa w kodzie BCD. Parametr OUTPUT_BITS określa (linia 3), ile bitów ma mieć wyjście modułu. W normalnych warunkach jest to czterokrotność liczby cyfr i nie ma potrzeby zmieniać tej praktyki, ale wspomniany parametr może zostać użyty do celowego wprowadzania błędów, by sprawdzić, co się stanie, jeżeli liczba bitów wyjścia okaże się niewystarczająca.

Generator sygnału zegarowego skonstruowany jest tak samo, jak we wszystkich poprzednich odcinkach kursu.

Na kolejnym etapie deklarujemy różne zmienne. Przejdźmy od razu do linii 4, w której tworzymy zmienną Start typu reg. Zmienna ta służyć będzie do sterowania wejściem Start_i testowanego modułu, a stan wysoki spowoduje uruchomienie konwersji. Linię niżej deklarujemy zmienną Done typu wire, która służyć będzie do oczekiwania na zakończenie konwersji. W linii 6 tworzymy zmienną Binary – jej celem będzie wysterowanie wejścia Binary_i. Zmienna inicjalizowana jest w ciekawy sposób: za pomocą operatora konkatenacji inicjalizujemy każdy z jej bitów wartością X, czyli wartością niezdefiniowaną. Chodzi o to, by testbench ustawiał jakąś konkretną wartość tej zmiennej tylko wtedy, kiedy będzie ona odczytywana przez testowany moduł. W linii 7 znajduje się zmienna BCD typu wire, która będzie przekazywać wynik z wyjścia BCD_i modułu Double Dabble do tasku, który ma zweryfikować, czy wynik jest prawidłowy.

Przydadzą się jeszcze dwie zmienne typu integer, które posłużą do ułatwienia obliczeń. Zmienna MaxInput z linii 8 określa maksymalną liczbę, jaką można przekonwertować. Wynika ona z liczby bitów wejścia, określonej parametrem INPUT_BITS. W linii 9 tworzymy iterator pętli for.

W linii 10 tworzymy instancję testowanego modułu. Łączymy jej wejścia i wyjścia ze zmiennymi zdefiniowanymi wcześniej. Omińmy póki co task weryfikujący działanie modułu i przeskoczmy do sekwencji testowej.

W linii 21 mamy pętlę for, której zadaniem jest przetestowanie wszystkich liczb możliwych do konwersji (od zera do wartości maksymalnej). Praca wewnątrz pętli podzielona została na trzy etapy.

W pierwszym (linia 22) kopiujemy wartość iteratora pętli i do zmiennej Binary, połączonej z wejściem testowanego modułu. Wartością tą będzie liczba, którą moduł ma przekonwertować z formatu binarnego na BCD. Następnie ustawiamy zmienną Start w stan wysoki, aby poinformować moduł, że ma odczytać swoje wejście danych i rozpocząć pracę.

W kolejnym takcie zegarowym (linia 23) ustawiamy zmienną Binary w stan nieistotny, podobnie jak to robiliśmy podczas jej deklarowania w linii 6. Musimy także wyzerować zmienną Start, bo w przeciwnym razie moduł rozpoczynałby pracę w każdym kolejnym takcie zegarowym.

Musimy poczekać, aż moduł skończy pracę (linia 24) i udostępni wynik na swoim wyjściu. Czekamy na pojawienie się stanu wysokiego na wyjściu Done. Wtedy uruchamiamy task weryfikujący, przekazując mu poprzez argument iterator pętli, czyli liczbę do konwersji, a także wynik obliczeń.

W linii 25 mamy kolejną, bardzo podobnie działającą pętlę. Wykonuje ona te same czynności, lecz iterator pętli zmniejsza się od wartości maksymalnej do zera.

Omówimy teraz sposób, w jaki testbench będzie sprawdzać, czy wynik zwrócony przez testowany moduł jest prawidłowy. Podczas symulacji moduł wykona ileś konwersji, a weryfikacja każdej z nich może dać wynik pozytywny lub negatywny. Potrzebujemy więc dwóch liczników do zliczania wyników każdej weryfikacji. W linii 11 tworzymy zmienną PassCounter, która będzie zwiększana o 1 po każdej pozytywnej weryfikacji, a linię niżej tworzymy zmienną FailCounter, która będzie inkrementowana w przypadku, gdy moduł zwróci wynik inny niż oczekiwany. Chcemy oczywiście, by po zakończeniu symulacji zawartość licznika FailCounter była równa zeru.

Task Verify rozpoczynamy w linii 13. Ma on dwa wejścia: Binary – które jest liczbą binarną do przekonwertowania na kod BCD – oraz wejście BCD, do którego powinna zostać doprowadzona ta sama liczba, lecz oczywiście w formacie BCD.

Metoda weryfikacji prezentuje się następująco: task ma za zadanie przeliczyć otrzymaną liczbę w formacie BCD na format binarny i porównać z liczbą, otrzymaną na wejściu Binary. Przeliczanie odbywa się w pętli for (linia 18). Iteratorem pętli jest zmienna Digit, która zmienia się od zera do OUTPUT_DIGITS.

W każdym obiegu pętli odczytujemy kolejną cyfrę BCD, po czym mnożymy ją przez 10 podniesione do potęgi równej iteratorowi pętli. Tak otrzymany wynik dodajemy do obecnej wartości zmiennej Result. Mówiąc konkretniej, jeżeli na wejściu BCD mamy liczbę 123, to pętla wykonuje działanie 3·100+2·101+1·102 i tak obliczony wynik zapisuje do zmiennej Result.

Zwróć uwagę, gdzie zadeklarowane są zmienne Digit oraz Result. Pierwsza z nich powstaje przed blokiem begin-end (linia 14), a druga na początku tego bloku (linia 16), po czym jest inicjalizowana zerem (linia 17). Zrobiłem to specjalnie, by pokazać, że zmienne wewnątrz tasku można tworzyć na dwa sposoby. Zapamiętaj, że jeżeli chcesz utworzyć zmienną wewnątrz bloku begin-end, to ten blok musi być jakoś nazwany, nawet jeżeli ta nazwa nigdzie nie będzie używana. W przykładowym kodzie blok nazwałem VerifyTask (linia 15).

W linii 18 mamy wspomnianą wcześniej pętlę for, a w linii 19 – porównujemy wynik otrzymany na wejściu BCD z wynikiem obliczonym przez task. Porównania dokonujemy za pomocą operatora === a nie == (linia 19). Jest to istotne z tego powodu, że w języku Verilog istnieje wartość nieokreślona x. Taką wartość mają między innymi zmienne, którym nie przypisano wartości początkowej. Mogłoby się zdarzyć, że w wyniku błędnie napisanego kodu, na którymś wejściu tasku pojawią się wartości nieokreślone i zostaną one przekazane do porównania, a w rezultacie dostaniemy nieokreślony wynik. Operator === porównuje dokładnie wszystkie bity, uwzględniając wartości nieokreślone, a nawet stan wysokiej impedancji. Jeżeli zostaną wykryte jakiekolwiek różnice między porównywanymi zmiennymi, wówczas operator zwróci fałsz.

W zależności od wyniku porównania, zwiększamy zmienną PassCounter lub FailCounter. W przypadku negatywnego wyniku weryfikacji, wyświetlamy komunikat na konsoli za pomocą funkcji $display(), aby ułatwić szukanie błędu (linia 20), po czym symulacja wykonywana jest dalej. Jeżeli wykrycie błędu ma natychmiast zakończyć symulację, można posłużyć się funkcją $fatal().

Na samym końcu symulacji wyświetlamy informację, ile testów zakończyło się pozytywną weryfikacją (linia 26), a ile razy uzyskano wynik negatywny (linia 27).

Aby wykonać symulację w symulatorze Icarus Verilog, uruchom skrypt, który zaprezentowano na listingu 3 lub wpisz opisane polecenia ręcznie w konsoli systemowej.

Po przeprowadzeniu symulacji powinieneś zobaczyć zapisy podobne do tych widniejących na listingu 4. Symulator przetestował 512 różnych wariantów i nie znalazł ani jednego błędu.

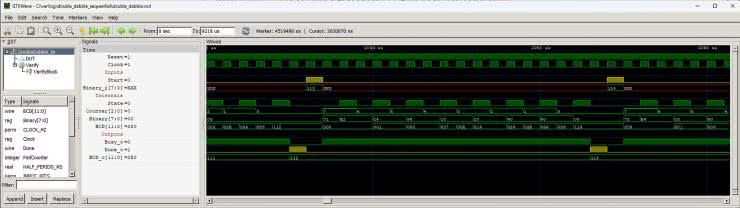
Otwórz plik wynikowy w przeglądarce GTKWave i skonfiguruj ją tak, by uzyskać efekt widoczny na rysunku 3. Przybliżyłem obraz na proces konwersji liczby 113 – właśnie taką konwertowaliśmy w przykładzie na początku tego odcinka. Zerknij ponownie na rysunek 2 i spróbuj znaleźć podobieństwa.

Rysunek 3. Okno symulacji

Moduł top

Przetestujmy nasz nowy moduł w praktyce na prawdziwym FPGA, za pomocą płytek MachXO2 Mega oraz User Interface Board, które zostały zaprezentowane w EP 09/2023 i można je nabyć w sklepie AVT. Opracujemy aplikację testową, w której zastosujemy enkoder obrotowy do sterowania licznikiem. Obrót w prawo będzie zwiększał licznik o 1, a w lewo będzie zmniejszał o 1. Licznik będzie miał możliwość liczenia od 0 do 9999. Zastosujemy również sterownik 8-cyfrowego wyświetlacza 7-segmentowego. Cztery cyfry po prawej stronie wyświetlacza będą pokazywać stan licznika w formacie szesnastkowym, tak jak to robiliśmy dotychczas. Natomiast cztery cyfry po lewej będą pokazywać stan licznika w zapisie dziesiętnym, po przekonwertowaniu przez moduł Double Dabble opracowany w tym odcinku kursu.

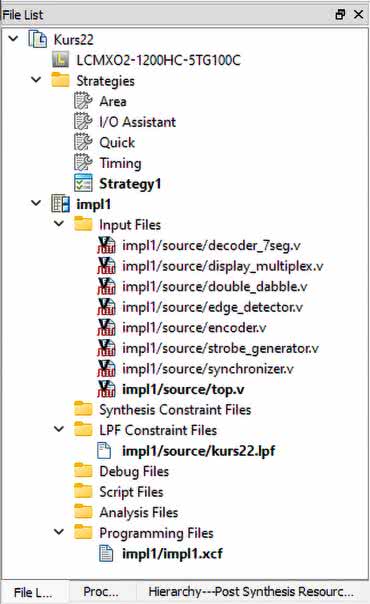
Utwórz nowy projekt i dodaj do niego pliki, które widać w drzewku projektowym na rysunku 4.

Rysunek 4. Drzewko projektu

Wszystkie pliki omawialiśmy już w poprzednich odcinkach kursu. Możesz je pobrać z repozytorium na GitHubie, dostępnego pod adresem [1], a cały projekt znajdziesz w programie Diamond pod adresem [2].

Weźmy na warsztat kod modułu top, pokazany na listingu 5. Oprócz wejścia zegara i resetu, moduł posiada wejścia, które odczytują piny enkodera obrotowego – oraz wyjścia sterujące wyświetlaczem. Elementy te omówione zostały w odcinkach numer 9 i 14.

Obsługą enkodera zajmuje się moduł Encoder, którego instancję tworzymy w linii 2. Zmienne sygnalizujące wykrycie obrotu w prawo i w lewo to Increment oraz Decrement typu wire, które tworzymy w linii 1. Wykrycie takiego zdarzenia powoduje ustawienie stanu wysokiego na długość jednego taktu sygnału zegarowego.

W linii 3 tworzymy 16-bitowy licznik Counter – jego celem jest zliczenie impulsów z enkodera. Poniżej mamy blok always, w którym zaimplementowano logikę licznika. Licznik ma zmieniać swoją wartość od 0 do 9999, zatem jeżeli ustawiony jest na wartość maksymalną i wtedy nadejdzie żądanie inkrementacji, musimy ustawić go w stan 0 (linia 4). Podobnie w drugą stronę: jeżeli obecna wartość licznika to 0 i sygnał dekrementacji jest w stanie wysokim, to trzeba go ustawić na wartość maksymalną (linia 5).

Powinniśmy wprowadzić prostą linię opóźniającą o jeden takt zegarowy dla sygnału wyzwalającego konwersję. Pomyślmy. Sygnał inkrementacji lub dekrementacji jest ustawiany na jeden cykl zegara. W następnym cyklu licznik ulega zwiększeniu lub zmniejszeniu. Konwersję należy zatem uruchomić dopiero w kolejnym takcie po zmianie stanu licznika.

Najprościej ten problem rozwiązać, wprowadzając opóźnienie w postaci zwyczajnego przerzutnika D. Taką rolę odgrywa 1-bitowa zmienna ConversionStart typu reg, którą tworzymy w linii 6. Logikę przerzutnika D opisujemy w osobnym bloku always poniżej. W każdym cyklu zegarowym wpisujemy do niego stan sygnałów Increment lub Decrement połączonych bramką OR (linia 7).

Przejdźmy do instancji modułu konwertera Double Dabble w linii 9. Kiedy wejście Start_i – do którego doprowadzono zmienną ConversionStart – znajduje się w stanie wysokim, rozpoczyna się konwersja danych na wejściu Binary_i, do którego doprowadzono licznik Counter. Po jakimś czasie wynik jest udostępniany na wyjściu BCD_o, skąd przesłany zostanie do kolejnych modułów za pośrednictwem 16-bitowej zmiennej Decimal typu wire, utworzonej w linii 8. Nie korzystamy z wyjść Busy_o ani Done_o, ponieważ moduł wyświetlacza działa ciągle i nie trzeba go informować, że stan jego wejść się zmienił.

Ostatni moduł, którego instancję tworzymy w linii 10, to moduł sterownika wyświetlacza DisplayMultiplex. Wielokrotnie był on już używany w poprzednich odcinkach. Na jego 32-bitowe wejście Data_i (linia 11) dostarczamy 16-bitowy stan licznika Counter oraz 16-bitowy wynik konwersji Decimal. Obie te zmienne sklejamy w jedną za pomocą operatora konkatenacji {}.

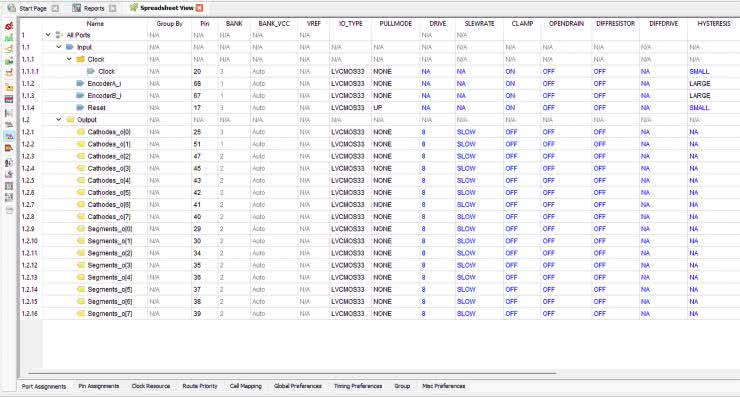
Uruchom syntezę, a następnie skonfiguruj piny w narzędziu Spreadsheet w taki sposób, jak to pokazano na rysunku 5. Pamiętaj, by na dole okna kliknąć zakładkę Timing Preferences i ustawić częstotliwość 25 MHz dla wejścia Clock.

Rysunek 5. Konfiguracja pinów w Spreadsheet

Po wygenerowaniu bitstreamu i wgraniu go do FPGA, powinieneś zobaczyć cyfrę 0 po prawej stronie wyświetlacza (moduł DisplayMultiplex wygasza nieistotne zera i traktuje dane na wejściu jako jedną liczbę). Pokręć dekoderem E41 w prawo lub w lewo, a stan licznika na wyświetlaczu będzie się zmieniał.

Przykład operacji pokazano na fotografii 1. Po lewej stronie widzimy liczbę dziesiętną 255, co w zapisie szesnastkowym ma postać: FF – i właśnie taka liczba jest wyświetlana po prawej stronie.

Fotografia 1. Płytka testowa podczas pracy

Algorytm Double Dabble w wersji sekwencyjnej jest łatwy i wymaga niewiele zasobów sprzętowych. Jego wadę stanowi fakt, że musimy czekać pewną liczbę taktów zegarowych na uzyskanie wyniku, a im większe liczby chcemy przekonwertować, tym dłużej potrwa oczekiwanie. Opisany algorytm da się zaimplementować także w wersji kombinacyjnej – czyli bez żadnego sygnału zegarowego. Tym zajmiemy się w kolejnym odcinku.

Dominik Bieczyński
leonow32@gmail.com