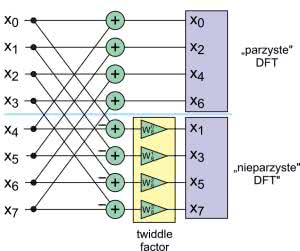
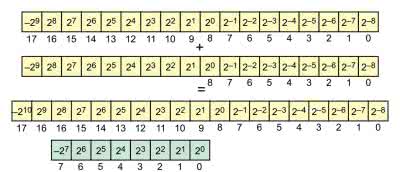
Rozpisaliśmy transformatę Fouriera o długości N, na dwie transformaty o połowę mniejszej długości. Teraz musimy wykonać pewne działania na współczynnikach, a następnie policzyć jedną transformatę dla współczynników parzystych, a drugą dla nieparzystych. W pierwszej, współczynniki wejściowe są po prostu sumą, lecz przygotowanie danych dla drugiej jest bardziej skomplikowane – najpierw liczymy różnice, a następnie musimy pomnożyć przez współczynnik, co w języku angielskim nosi nazwę „twiddle factor”. Schematycznie pokazuje to rysunek 7.
Po lewej stronie, w pionie widzimy wszystkie osiem współczynników, zebranych w dziedzinie czasu. Górne cztery wiersze pokazują przygotowanie współczynników do transformaty „nieparzystej”. Widzimy tu cztery sumy postaci
![]()
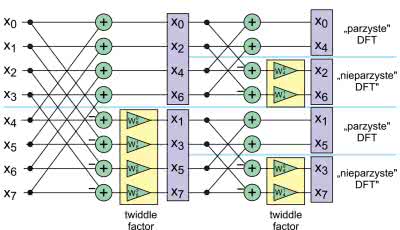
Podzieliliśmy nasze zadanie na dwa mniejsze. Musimy teraz policzyć dwie kolejne transformaty. Możemy użyć tu dowolnej metody, na przykład policzyć ze wzoru. My jednak użyjemy jeszcze raz (a w zasadzie to dwa razy) naszego podziału. Uzyskany wynik pokazuje rysunek 8, gdzie zobaczymy dwa analogiczne podziały. Zamiast jednej transformaty 8-punktowej, mamy do policzenia cztery, ale za to każda z nich ma rozmiar 2.
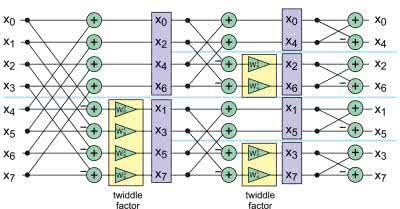
Musimy więc przejść do kolejnego, trzeciego kroku. Tym razem będzie to koniec naszego rekurencyjnego podejścia: dotarliśmy do warunku końcowego. Transformata dwuelementowa jest na tyle łatwa, że rozpiszemy ją po prostu z definicji:
Kiedy przyjrzymy się definicji zauważymy, że jest to taki sam motylek jak poprzednie, ale tym razem „tweedle factor” jest równy 1. Możemy więc dorysować ostatni etap obliczeń. Całość znajduje się na rysunku 9. Spróbujmy policzyć, czy takie podejście ma sens. Każdy podział, niezależnie od rzędu, wymaga wykonania N/2 mnożeń zespolonych. Jak łatwo sprawdzić dla N próbek, algorytm będzie wymagał log2N etapów. Aby uzyskać wynik, niezbędnych było N/2log2N mnożeń. Widzimy więc, że FFT pozwala na zredukowanie złożoności algorytmu z N2 na znacznie wydajniejszy Nlog2N.
Pozostała jeszcze jedna kwestia – widzimy że kolejność wyników na wyjściu, została dość mocno przemieszana. Wyjaśni się to, gdy zapiszemy numery współczynników w systemie binarnym. W pierwszych dwóch kolumnach widzimy kolejność współczynników na wejściu: najpierw w systemie dziesiętnym, a później binarnym. W każdym kroku dokonujemy podziału na dwie transformaty: parzystą i nieparzystą. Parzystość rozróżniamy po najmłodszym bicie liczby (kolor czerwony w kolumnie 2). W Kroku1 najpierw pojawiają się liczby parzyste – pierwsza transformata, a później nieparzyste – druga transformata.
Ten sam proces ma miejsce w kolejnym kroku, jednak tym razem w pierwszej transformacie mamy po kolei liczby 0, 2, 4 i 6. Do transformaty „parzystej” pójdą te wartości, gdzie kolejny bit będzie zerem (w Kroku1 zaznaczone na czerwono). Analogiczna sytuacja zachodzi w Kroku2, ale tym razem mamy już tylko dwie wartości, więc kolejność już się nie zmieni. Kiedy przjrzymy się kolumnie Koniec, zauważymy że bity w niej zawarte są lustrzanym odbiciem tych z kolumny Start (kolejność ta po angielsku nosi nazwę „bit reversal”). Rozumowanie to można przeprowadzić dla dowolnego N.
Opisany sposób obliczeń jest jedną z wielu metod szybkiego obliczania DFT. Nosi on nazwę algorytm Cooleya-Tukeya, z decymacją w dziedzinie częstotliwości.
Sprzęt
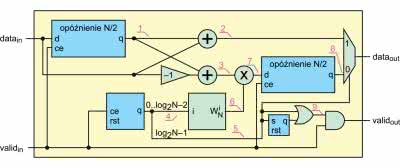
Znamy już algorytm, ale musimy go dostosować do implementacji w układzie FPGA. Rysunek 10 pokazuje projekt pojedynczego „motylka”, który widzieliśmy już na rysunku 7, lecz tym razem nasze dane wejściowe to ciąg próbek (zespolonych) z sygnałem poprawności (valid).
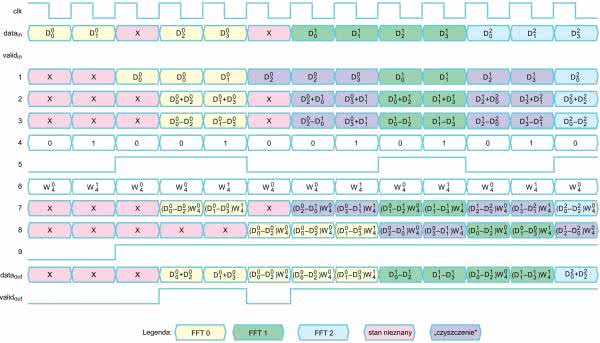
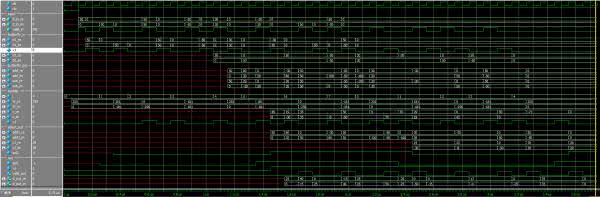
Na rysunku 11 pokazano przepływ danych dla przypadku N=4. Numery odpowiadają przebiegom zaznaczonym na schemacie. Najpierw dane wejściowe trafiają na linię opóźniającą o długości N/2, gdzie N jest długością FFT. Jej wyjście widoczne jest w wierszu (1). Zapisywane są tylko „poprawne” sygnały, co uzyskujemy sterując wejściem CE, za pomocą sygnału valid. Następnie odbywa się obliczenie sumy i różnicy pomiędzy sygnałem (1), a danymi wejściowymi. Ich wyniki znajdziemy w (2) i (3).
Kiedy wczytywana jest pierwsza połowa danych, na wyjściu linii opóźniającej są śmieci, albo wartości z poprzedniego cyklu obliczeń. Wtedy sygnały z punktów (2) i (3) nie mają sensu. Na tym etapie następuje wczytywanie danych. Kiedy zostanie wczytana połowa próbek, wtedy gdy w punkcie (1) znajduje się próbka i, natomiast w danych wejściowych przychodzi próbka i+N/2. Przez kolejnych N/2 próbek wejściowych nastąpi wykonywanie obliczeń.
Równocześnie każda kolejna próbka powoduje inkrementację licznika modulo N. Jego najstarszy bit (5) posłuży nam do sterowania wyjściem, pozostałe – do wygenerowania odpowiednich współczynników (znanych nam już „tweedle factor”). Są one generowane przez osobny moduł i pojawiają się w punkcie (6). Po przemnożeniu przez różnicę, wynik pojawia się w punkcie (7).
Najpierw następuje wczytywanie pierwszej połowy danych, a podczas wczytywania drugiej połowy, otrzymujemy po dwie próbki wyjściowe naraz.
Dlatego na wyjściu pojawia się kolejna linia opóźniająca, także o długości N/2 (przechowa ona połowę wyników). Sygnał (5) decyduje, czy na wyjściu pojawi się sygnał (2) lub (8). Kiedy rozpoczynamy obliczanie kolejnego „motylka”, sygnał (5) ma wartość 0, a gdy dostępne są pierwsze wyniki, licznik osiągnie wartość N/2 i sygnał (5) będzie miał wartość 1. Dlatego z początku na wyjście przekazane zostaną próbki z (2). Jeżeli wczytane zostaną wszystkie dane wejściowe, wypełniona zostanie wyjściowa linia opóźniająca, a licznik próbek „przekręci się” i będzie miał wartość 0. Druga część wyniku jest następnie „wypychana” przez pierwszą połowę próbek z następnej iteracji.
Wejściowy sygnał valid jest niemal dokładnym odwzorowaniem sygnału wejściowego. Musimy go jednak wygasić przez N/2 próbek z pierwszej iteracji. Wtedy w linii opóźniającej znajdują się śmieci. Służy do tego przerzutnik i bramka OR. Sygnał w punkcie (9) przyjmuje stan wysoki, gdy pierwsze poprawne dane dostaną się na wyjście, i pozostaje taki aż do resetu.
Na rysunku 11 pokazano przebieg obliczeń dla dwóch kolejnych iteracji, nazwanych FFT0 i FFT1 i oznaczonych odpowiednio kolorem żółtym i zielonym. Na końcu pojawiają się także próbki z trzeciej iteracji (kolor niebieski), które „wypychają” wyniki drugiej iteracji. X (kolor czerwony) oznacza stan nieustalony. Kolor fioletowy pokazuje moment, gdy następuje wczytywanie danych dla kolejnej iteracji, z równoczesnym wysyłaniem końcówki wyniku z poprzedniej. Obliczenia mieszają dane z dwóch cykli. Nie jest to jednak problem, gdyż wyjściowy multiplekser nigdy nie wypuści tych sygnałów na zewnątrz modułu.
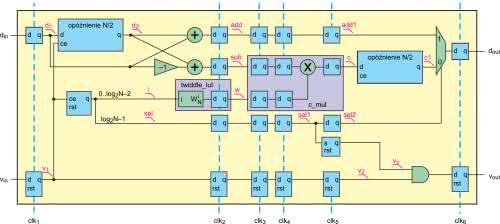
Schemat z rysunku 10 jest uproszczony. Zawiera jedynie „logikę”, natomiast pominięte są opóźnienia „techniczne”, wymagane do implementacji w układzie FPGA. Uzupełniony schemat pokazuje rysunek 12. Widzimy, że przepłyniecie danych przez moduł, zajmuje sześć cykli zegara. Najpierw mamy rejestry wejściowe. Drugi takt pozwala na „zatrzaśnięcie” wyników dodawania i odejmowania. Także odczytanie współczynników „tweedle factor” z pamięci RAM, zajmuje jeden cykl. Następnie widzimy moduł mnożenia zespolonego c_mul, który zaprojektowaliśmy w poprzednim odcinku. Jego wykonanie zajmuje trzy kolejne takty. Na samym końcu mamy rejestr wyjściowy z modułu. Aby wszystkie sygnały „płynęły razem” na wszystkich liniach, zostały dodane przerzutniki. Uproszczeniu uległ sposob generowania wyjściowego sygnału valid. Zamiast bramki LUB wykorzystujemy sygnał z jednego cyklu zegara wcześniej.
Generowanie „tweedle factor”
Implementację zaczniemy od generatora współczynników (listing 1). Zastosujemy najprostszą metodę, czyli tablicowanie. Wartości kolejnych współczynników obliczymy wcześniej i zapiszemy w pamięci.
10 parameter real pi = 3.14159265358979323846;
11
12 module twiddle_lut #(
13 parameter N = 2,
14 parameter LOG_N = $clog2(N/2),
15 parameter K = 9,
16 parameter file_name = N
17 ) (
18 input wire clk,
19 input wire [LOG_N-1:0]i,
20 output logic signed [K-1:0]W_re,
21 output logic signed [K-1:0]W_im
22 );
23 logic [2*K-1:0]W[N/2-1:0];
24
25 always_ff @(posedge clk)
26 {W_re, W_im} <= W[i];
27
28 initial begin
29 //synthesis translate_off
30 real MAX = (2**(K-1)-1.0);
31 for (int i = 0; i < N/2; i++) begin
32 real angle, rW_re, rW_im;
33 logic signed [K-1:0] W_re;
34 logic signed [K-1:0] W_im;
35 angle = -2*pi*i/N;
36 rW_re = 2**(K-1)*$cos(angle);
37 rW_im = 2**(K-1)*$sin(angle);
38 W_re = (rW_re > MAX) ? MAX : rW_re;
39 W_im = (rW_im > MAX) ? MAX : rW_im;
40 W[i] = {W_re, W_im};
41 end
42 case (N)
43 4 : $writememb("04.mem", W);
44 8 : $writememb("08.mem", W);
45 16: $writememb("16.mem", W);
46 32: $writememb("32.mem", W);
47 endcase
48 // synthesis translate_on
49 case (N)
50 4 : $readmemb("04.mem", W);
51 8 : $readmemb("08.mem", W);
52 16: $readmemb("16.mem", W);
53 32: $readmemb("32.mem", W);
54 endcase
55 end
56
57 endmodule
Na początku deklarujemy stałą pi, którą użyjemy do obliczeń. Sam moduł zaczyna się w wierszu 12. Najpierw deklarujemy cztery parametry, ale tylko dwa z nich konfigurujemy. N oznacza długość, natomiast K liczbę bitów przypadających na jedną liczbę. Sam blok ma dwa wejścia: zegarowe clk i oznaczające wartość wykładnika; oraz dwa wyjścia: część rzeczywista i urojona współczynnika.
Sama pamięć jest zdefiniowana w linii 23. Mamy tu N/2 słów o długości 2K bitów: po K dla części rzeczywistej i urojonej. Odczytywanie z ROM ma miejsce w bloku always_ff. Na końcu, w bloku initial, znajduje się generowanie współczynników. Niestety, funkcje trygonometryczne są niesyntezowalne, więc użyty tu jest taki sam trik jak wcześniej przy tablicowaniu funkcji sinus. Wartości są generowane w symulacji i zapisywanie do pliku, który potem jest wczytywany przy syntezie. Nie znalazłem sposobu na stworzenie nazwy pliku na podstawie parametru N, która działałaby zarówno w środowisku Quartus 18 jak i ModelSim, więc w tym celu użyłem bloku case (linie 42…54). Chcąc wykorzystać kod dla N większych od 32, trzeba go rozszerzyć.
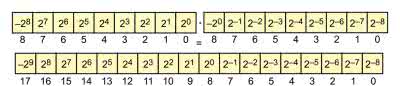
Samo wyliczanie współczynników odbywa się w pętli for (wiersze 31…41). Najpierw w zmiennej angle zapisywana jest aktualna wartość wykładnika. Później obliczane są wartości sinusa i cosinusa, które zostały pomnożone przez 2K-1, ponieważ współczynniki zapisane są w formacie stałoprzecinkowym ze znakiem. Znaczenie kolejnych bitów w tej reprezentacji pokazuje rysunek 13. Najstarszy bit znaku ma wagę –1, natomiast pozostałe odpowiadają kolejnym ułamkom: 0,5, 0,25, aż do 2-8. Łatwo policzyć, że możemy zapisać liczby od -1, do około 0,996 (255/256).
Dlatego, aby uniknąć przepełnienia w liniach 38 i 39, wartości większe są „przycinane”.
Testbench dla modułu znajdziemy w 13_fft/twiddle_lut_tb.sv. Sprawdzana w nim jest instancja dla N=32. Aby uruchomić symulację w programie ModelSim, wywołujemy:
do twiddle_lut_sim.do
Uzyskany wynik jest podobny do tego z rysunku 14, gdzie widzimy połowę funkcji trygonometrycznych. Dla części rzeczywistej jest to cosinus, a dla urojonych – sinus.
Motylek
Czas na implementację „motylka” z rysunku 12. Nazwy poszczególnych sygnałów użytych w kodzie są takie same, jak te naniesione na rysunku. Zachęcam do otworzenia pełnego kodu źródłowego i porównania go ze schematem. Sam moduł zdefiniowany jest na listingu 2 i przyjmuje on dwa parametry. Tak jak poprzednio N to długość transformaty, a K to liczba bitów dla danych wejściowych.
10 module butterfly #(
11 parameter K = 8,
12 parameter N = 2,
13 parameter LOG_N = $clog2(N)
14 ) (
15 input wire clk,
16 input wire rst,
17 input wire signed [K-1:0]d_in_re,
18 input wire signed [K-1:0]d_in_im,
19 input wire valid_in,
20 output logic signed [K-1:0]d_out_re,
21 output logic signed [K-1:0]d_out_im,
22 output logic valid_out
23 );
Dalej znajdziemy sygnały wejściowe. Są to po kolei zegar clk, reset rst, sygnał valid_in oraz dane wejściowe: rzeczywiste d_in_re i urojone d_in_im. Sygnały wyjściowe są trzy: część rzeczywista (d_out_re) i urojona (d_out_im) danych oraz sygnał valid_out.
51 delay #(.N(N/2), .L(2*K)) d_d1 (
52 .clk(clk),
53 .rst(1’b1),
54 .ce(v1),
55 .in({d1_re, d1_im}),
56 .out({d2_re, d2_im}));
57
58 always_ff @(posedge clk) begin
59 add_re <= d2_re + d1_re;
60 add_im <= d2_im + d1_im;
61 sub_re <= d2_re – d1_re;
62 sub_im <= d2_im – d1_im;
63 end
Część odpowiedzialną za wczytywanie danych pokazuje listing 3. Linia opóźniająca została zrealizowana za pomocą modułu delay. Ponieważ ścieżka danych nie wymaga resetu, jej wejście rst zostało na stałe przypisanie do stanu 1 (reset aktywowany jest stanem niskim). Definicję modułu znajdziemy w pliku 13_fft/delay.sv. Przyjmuje on dwa parametry: N jest długością, a L liczbą bitów w słowie. Dodawanie i odejmowanie zespolone zostało zrealizowane w liniach 58…63. Osobno obliczamy część rzeczywistą i urojoną. Wszystkie czynniki zapisane są na K bitach, co oznacza, że do przedstawienia zarówno sumy jak i różnicy potrzebujemy K+1 bitów i taką właśnie długość mają przechowujące je wektory.
079 generate
080 if (N > 2) begin
081 twiddle_lut #(.N(N), .K(K+1)) twiddle (
082 .clk(clk),
083 .i(i[LOG_N-2:0]),
084 .W_re(W_re),
085 .W_im(W_im));
086 end else begin
087 assign W_re = 2**K-1;
088 assign W_im = ‘0;
089 end
090 endgenerate
093 c_mul #(.K(K+1)) mul (
094 .clk(clk),
095 .rst(rst),
096 .a_re(sub_re),
097 .a_im(sub_im),
098 .b_re(W_re),
099 .b_im(W_im),
100 .c_re(c_re),
101 .c_im(c_im));
133 always_ff @(posedge clk)
134 {d_out_re, d_out_im} <= sel2 ?
135 {add1_re[K:1], add1_im[K:1]} :
136 {c1_re[K:1], c1_im[K:1]};
Ostatni fragment, któremu przyjrzymy się dokładniej, to mnożenie przez „tweedle factor” (listing 4). Moduł pamięci ze współczynnikami umieszczony jest wewnątrz bloku generate (linie 79…90). Dzięki temu możemy zastosować instrukcję if. LUT zostanie umieszczony jedynie dla N większych o 2, natomiast dla najmniejszego przypadku przypiszemy na stałe liczbę 1+0j (dokładniej 255/256+0j, ponieważ liczba 1 jest poza zakresem naszej zmiennej).
Dalej znajduje się blok c_mul, realizujący mnożenie zespolone. Rysunek 15 pokazuje czynniki w mnożeniach rzeczywistych. Dane są pokazane jako liczba całkowita ze znakiem, a współczynniki W jako liczba stałoprzecinkowa. W wyniku mnożenia tych dwóch liczb, otrzymujemy 18-bitową liczbę stałoprzecinkową. Jej najmłodszy bit, tak jak poprzednio, ma wagę 1/256.
Kolejnym krokiem w mnożeniu zespolonym jest dodawanie (rysunek 16). W wyniku zsumowania otrzymaliśmy liczbę 19-bitową. Jednak na wejściu nasz motylek spodziewa się liczby 8-bitowej. Na wyjście przekazane są bity od 9 do 16 (zaznaczone kolorem zielonym). Wybór dokonywany jest wewnątrz modułu c_mul oraz w linii 135. W wyniku tego „wycięcia” następuje podzielenie wyniku przez dwa. Obcięte są także dwa najstarsze bity. Dla sygnałów wejściowych o dużej amplitudzie może to spowodować przepełnienie. W takim przypadku można dodać saturację.
055 initial begin
056 valid_in = 1’b0;
057 rst = 1’b0;
058 #100ns @(negedge clk);
059 rst <= 1’b1;
060 for (int i = 0; i < 3*N/2; i++) begin
061 valid_in = 1’b1;
062 if (i < N) begin
063 d_in_re = in_re[i];
064 d_in_im = in_im[i];
065 end
066 @(posedge clk);
067 valid_in = 1’b0;
068 d_in_re = ‘0;
069 d_in_im = ‘0;
070 @(posedge clk);
071 if (i % 3) @(posedge clk);
072 end
073 valid_in = 1’b0;
074 end
075
076 butterfly #(.K(K), .N(N)) dut (
077 .clk(clk),
078 .rst(rst),
079 .d_in_re(d_in_re),
080 .d_in_im(d_in_im),
081 .valid_in(valid_in),
082 .d_out_re(d_out_re),
083 .d_out_im(d_out_im),
084 .valid_out(valid_out));
085
086 always_ff @(posedge clk) begin
087 if (valid_out) begin
088 out_re[i] <= d_out_re;
089 out_im[i] <= d_out_im;
090 i <= i + 1;
091 end
092 if (i == N) begin
093 rms = 0;
094 for (int i = 0; i < N; i++) begin
095 if (i < N/2) begin
096 out_sim_re = in_re[i] + in_re[i + N/2];
097 out_sim_im = in_im[i] + in_im[i + N/2];
098 end else begin
099 out_sim1_re = in_re[i-N/2] – in_re[i];
100 out_sim1_im = in_im[i-N/2] – in_im[i];
101 W_re = $cos(-2*pi*(i-N/2)/N);
102 W_im = $sin(-2*pi*(i-N/2)/N);
103 out_sim_re = out_sim1_re*W_re – out_sim1_im*W_im;
104 out_sim_im = out_sim1_re*W_im + out_sim1_im*W_re;
105 end
106 out_sim_re = out_sim_re / 2;
107 out_sim_im = out_sim_im / 2;
108 $display("s: %.2f+%.2fj h: %.2f+%.2fj",
109 out_sim_re, out_sim_im,
110 out_re[i], out_im[i]);
111 rms += (out_sim_re-out_re[i])**2 + (out_sim_im-out_im[i])**2;
112 end
113 rms = $sqrt(rms/N);
114 $display("RMS of error is %.1f", rms);
115 $stop;
116 end
117 end
Sam testbench naszego modułu został pokazuje listing 5. W bloku initial (linie 55…74) następuje wprowadzenie danych wejściowych. Najpierw przesyłanych jest N próbek sygnału, a później dodatkowe N/2, które „przepychają” wyniki obliczeń na wyjście. Następnie, w wierszach 76…84, znajdziemy instancję testowanego modułu.
Najciekawsza jest ostatnia część, gdzie zbieramy dane wejściowe i jeszcze raz obliczamy wynik. Tym razem jednak używamy rozkazów niesyntezowalnych. Samo zbieranie danych ma miejsce w liniach 87…91. Rachunki odbywają się dopiero po zakończeniu symulacji. Wykorzystane są operacje na liczbach zmiennoprzecinkowych, które zapewniają dużo większą precyzję. Oba wyniki są wyświetlane w linii 108. Na końcu (linia 111) jest liczony błąd średnio-kwadratowy pomiędzy nimi (czasami oznaczany jako RMS, od angielskiego Root Mean Square), obliczany jako:
gdzie xa to wynik symulacji, a xb obliczeń zmiennoprzecinkowych.
Symulację uruchamiamy skryptem:
do butterfly_sim.do
# s: 40.00+15.00j h: 40.00+15.00j
# s: -15.00+40.00j h: -15.00+40.00j
# s: 25.00+50.00j h: 25.00+50.00j
# s: 0.00+-50.00j h: 0.00+-50.00j
# s: 10.00+-15.00j h: 9.00+-15.00j
# s: 17.68+-3.54j h: 17.00+-4.00j
# s: 0.00+-25.00j h: 0.00+-25.00j
# s: 35.36+35.36j h: 35.00+35.00j
# RMS of error is 0.5
Rezultat pokazuje listing 6. Widzimy, że różnice w wyniku dotyczą jedynie części ułamkowej. Dlatego że wybraną metodą zaokrąglania jest „obcięcie”, uzyskany wynik nie jest najbliższy temu dokładnemu – jest to spodziewany efekt, wynikający z uproszczenia implementacji. Dla użytego wektora wejściowego, RMS błędu wynosi 0,5. Rysunek 17 pokazuje uzyskane przebiegi. Warto je porównać z uproszczonym diagramem z rysunku 11.
Podsumowanie
Jesteśmy coraz bliżej zbudowania analizatora widma dźwięku. Następnym etapem będzie połączenie kolejnych „motylków” w pełne FFT – zajmiemy się tym w kolejnej części cyklu.
Rafał Kozik
rafkozik@gmail.com
Przypisy :
[1] Repozytorium z przykładami, http://bit.ly/33uYPxs
[2] Lyons r.G., Wprowadzenie do cyfrowego przetwarzania sygnałów, Wydawnictwo Komunikacji i Łączności Warszawa 2010
[3] Film prezentujący działanie FFT, https://bit.ly/35H0yTp

 Zaloguj
Zaloguj