Drgania styków
Podczas przełączania znajdujących się na płytce przełączników DIP-switch występują tzw. drgania styków, które powodują, że na wejściu zamiast jednego zbocza otrzymamy całą serię impulsów. Gdybyśmy chcieli zliczać liczbę włączeń to zamiast jednego zliczylibyśmy kilka albo nawet kilkadziesiąt zdarzeń.
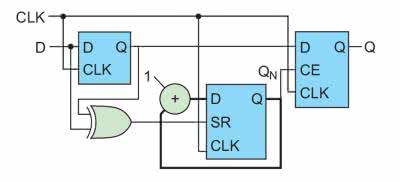
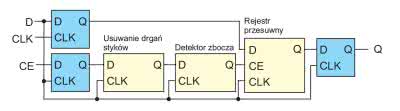
Jednym ze sposobów rozwiązania tego problemu jest korzystanie z wartości „zatrzaśniętej” w rejestrze. Jej wartość będziemy aktualizować tylko wtedy, gdy stan wejścia nie ulegnie zmianie przez zadany czas [1]. Schemat takiego układu pokazano na rysunku 1.
Wejściowy rejestr na każdym narastającym zboczu zegara zapisuje stan z wejścia D. Dzięki temu na jego wejściu mamy aktualną, a na wyjściu poprzednią wartość. Jeżeli jest ona stabilna oba wejścia bramki ex-or będą miały taką samą wartość. Zmiana stanu wejściowego spowoduje, że przez jeden cykl będą się one różnić, co pociągnie wystawienie na jej wyjściu jedynki logicznej i reset licznika. Gdy jednak stała wartość utrzyma się dostatecznie długo doliczy on w końcu do wartości 2N-1, (przy założeniu, że ma on długość N). Nastąpi wtedy odblokowanie trzeciego przerzutnika i wystawienie nowej wartości na wyjście Q. Jeżeli wartość wejściowa jest stała licznik będzie zliczał „w kółko”, a rejestr wyjściowy będzie aktywny przez połowę czasu. Jednak nie ma to znaczenia, ponieważ w przypadku zmiany stanu wejścia D licznik zostanie zresetowany, a na wejściu CE pojawi się stan niski, zanim nowa wartość zostanie zatrzaśnięta.
Przyglądnijmy się teraz implementacji w języku SystemVerilog (listing 1). Moduł przyjmuje jeden parametr – N pozwalający na konfigurację czasu, po którym sygnał zostanie uznany za stabilny. Ze światem komunikuje się poprzez 3 wejścia: zegarowe clk, asynchorniczny reset rst i wejście sygnału d oraz wyjście q.
10 module debounce
11 #(
12 parameter N=8
13 ) (
14 input wire clk,
15 input wire rst,
16 input wire d,
17 output logic q
18 );
19 logic [N-1:0]stable_time;
20 logic sr;
21 logic dr;
22
23 always_ff @(posedge clk or negedge rst)
24 if (!rst)
25 dr <= ‘0;
26 else
27 dr <= d;
28
29 assign sr = (d != dr);
30
31 always_ff @(posedge clk or negedge rst)
32 if (!rst)
33 stable_time <= ‘0;
34 else if (sr)
35 stable_time <= ‘0;
36 else
37 stable_time <= stable_time + 1;
38
39 always_ff @(posedge clk or negedge rst)
40 if (!rst)
41 q <= ‘0;
42 else if (stable_time[N-1])
43 q <= dr;
44 endmodule
W liniach 23 do 27 znajduje się wejściowy przerzutnik. Na każdym narastającym zboczu stan wejścia d jest wpisywany do zmiennej dr. Bramka EX-OR jest zrealizowana w linii 29 jako logika asynchroniczna. Sam licznik znajduje się w liniach od 31 do 37. W kolejnych wierszach widzimy reset asynchroniczny, reset synchroniczny oraz inkrementację. Ostatnią częścią (linie 39…43) jest przerzutnik wyjściowy, który jako sygnał clock enable (bramkowanie zegara) używa najstarszego bitu licznika stable_time.
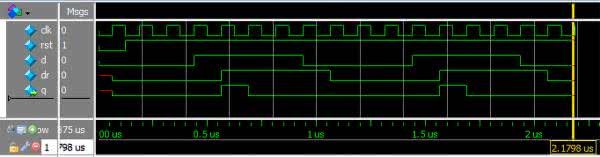
Do przetestowania działania modułu został przygotowany test bench, który znajduje się w pliku 03_shiftreg/debounce_tb.sv. Ponieważ jest podobny do tych, które znamy z poprzedniej części, nie będziemy go dokładnie analizować. Natomiast warto zapoznać się z nim we własnym zakresie. Aby go uruchomić w programie ModelSim możemy użyć skryptu 03_shiftreg/debounce_sim.do. Przechodzimy poleceniem cd do folderu z kodami źródłowymi i wywołujemy polecenie:
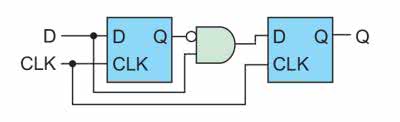
Schemat niezbędnego układu pokazano na rysunku 3. Pierwsza część jest analogiczna jak w poprzednim układzie filtra. Za pomocą pierwszego przerzutnika na wejście bramki podajemy aktualny i poprzedni stan sygnału wejściowego. Prezentowany układ wykrywa zbocza narastające. Oznacza to, że chcemy uzyskać stan wysoki gdy poprzednia wartość wejścia to 0, a aktualna to 1. Jak łatwo sprawdzić, taką funkcje realizuje bramka AND z zanegowanym jednym z wejść. Drugi przerzutnik nie jest niezbędny. Jego funkcją jest jedynie zapisanie aktualnego stanu. Ułatwia to późniejszą syntezę. Należy jednak pamiętać, że dodatkowy przerzutnik wprowadza opóźnienie o jeden cykl zegara.
Implementacja tego modułu jest stosunkowo krótka (listing 2).
10 module edge_detector (
11 input wire clk,
12 input wire rst,
13 input wire d,
14 output logic q
15 );
16 logic dr;
17
18 always_ff @(posedge clk or negedge rst)
19 if (!rst) begin
20 dr <= ‘0;
21 q <= ‘0;
22 end else begin
23 dr <= d;
24 q <= d & ~dr;
25 end
26 endmodule
Wejścia i wyjścia są analogiczne jak w module debonuce. Tym razem cała logika została umieszczona w jednym bloku always_ff. W liniach 19...21 zrealizowany jest asynchroniczny reset. W linii 23 znajduje się przerzutnik wejściowy, a w linii 24 bramka logiczna i rejestr wyjściowy. Tak jak poprzednio możemy sprawdzić działanie modułu w symulacji, poleceniem:
Rejestr przesuwny
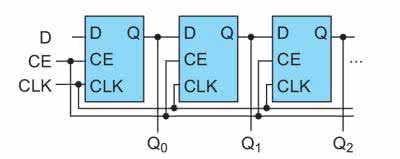
W dwóch poprzednich modułach używaliśmy przerzutnika D do opóźnienia sygnału o jeden takt zegara. Jeśli połączymy ze sobą wejścia i wyjścia kilku (w naszym module jest ich N) przerzutników otrzymamy rejestr przesuwny. Sygnał na wyjściu ostatniego z nich będzie opóźniony o N taktów zegara względem pierwszego. Schemat takiego układu pokazano na rysunku 5.
Implementacja została pokazana na listingu 3. Parametr N określa długość rejestru przesuwnego (liczbę przerzutników). Głowna część logiki znajduje się w bloku always_ff. W liniach 22...23 zrealizowany jest reset asynchroniczny. Wykorzystujemy tutaj przypisanie wartości ‘0, która oznacza wektor zer o takiej długości jak ten, który znajduje się po lewej stronie przypisania (analogicznie można stworzyć wektor samych jedynek za pomocą polecenia ‘1).
10 module shift_reg
11 #(
12 parameter N = 8
13 ) (
14 input wire clk,
15 input wire rst,
16 input wire ce,
17 input wire d,
18 output logic [N-1:0]q
19 );
20
21 always_ff @(posedge clk or negedge rst)
22 if (!rst)
23 q <= ‘0;
24 else if (ce) begin
25 q[0] <= d;
26 for (int i = 1; i < N; i++)
27 q[i] <= q[i-1];
28 end
29 endmodule
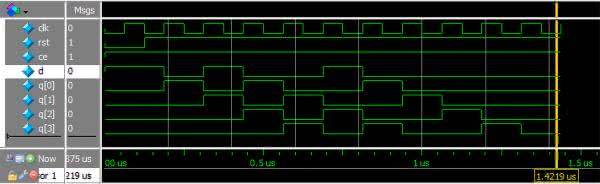
Ciekawsza jest druga część, gdzie realizujemy logikę rejestru przesuwnego. Najpierw w linii 25 znajduje się przerzutnik zerowy. Następnie pozostałe N-1 przerzutników jest wygenerowanych w pętli for. Jednak w przeciwieństwie do języków programowania tutaj nie zostanie ona wykonana iteracyjnie, ale spowoduje wygenerowanie działających równolegle bloków logik. Sprawdźmy jego działanie w symulacji:
Łączymy całość
Zebraliśmy już wszystkie bloki potrzebne do uruchomienia pierwszego eksperymentu. Będzie to rejestr przesuwny, którym będziemy sterować za pomocą przełączników dostępnych na płytce: jeden pozwoli na wybranie stanu wejścia D, a drugi na taktowanie poprzez zwalnianie wejścia CE na jeden cykl zegara. Sposób połączenia bloków pokazano na rysunku 7.
Pewnym niuansem pominiętym w tym projekcie jest nieuwzględnienie opóźnienia wprowadzonego przez filtrację drgań (2N+1 cykli zegara) oraz wykrywanie zbocza (1 cykl zegara). Tak więc sygnał na wejściu CE będzie opóźniony względem wejścia D o 2N+2 cykli zegara. W naszym przypadku nie zakłóci to działania, ponieważ „opóźnienia” wprowadzone przez przesuwającego przełączniki człowieka są dużo większe. Jednak w ogólnym przypadku należy zadbać o to, aby spotykające się sygnały miały względem siebie „odpowiednie” opóźnienie (tzw. latencję). Dodatkowo na wejściu i wyjściu dodane zostały rejestry, które pozwolą narzędziom na łatwiejsze rozłożenie elementów w strukturze układu FPGA.
Kod źródłowy zaprezentowano na listingu 4. Implementacja zaczyna się od przerzutników D zatrzaskujących stan wejść i wyjść (linie 23...32).
10 module shift_reg_led #(
11 parameter LED_N = 8
12 ) (
13 input wire clk,
14 input wire rst,
15 input wire ce_in,
16 input wire d_in,
17 output logic [LED_N-1:0]led
18 );
19 logic ce_in_r, d_in_r;
20 logic [LED_N-1:0]led_out;
21 logic ce, ce_db;
22
23 always_ff @(posedge clk or negedge rst)
24 if (!rst) begin
25 ce_in_r <= 1’b0;
26 d_in_r <= 1’b0;
27 led <= 1’b0;
28 end else begin
29 ce_in_r <= ce_in;
30 d_in_r <= d_in;
31 led <= led_out;
32 end
33
34 debounce #(.N(20)) db (
35 .clk(clk),
36 .rst(rst),
37 .d(ce_in_r),
38 .q(ce_db)
39 );
40
41 edge_detector ed (
42 .clk(clk),
43 .rst(rst),
44 .d(ce_db),
45 .q(ce)
46 );
47
48 shift_reg #(.N(LED_N)) sreg (
49 .clk(clk),
50 .rst(rst),
51 .ce(ce),
52 .d(d_in_r),
53 .q(led_out)
54 );
55 endmodule
Dalej zainstancjonowane są moduły: filtracji drgań, wykrywania zbocza oraz sam rejestr przesuwny. Przed przejściem do hardwareu sprawdźmy najpierw jak całość sprawdzi się w symulacji którą uruchamiamy rozkazem:
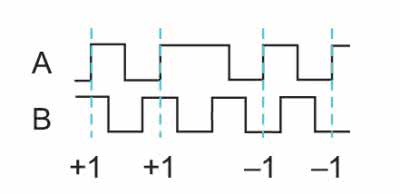
Enkoder posiada trzy złącza: A, B oraz masę. W czasie obrotu na wyjściach A i B pojawiają się przebiegi prostokątne przesunięte względem siebie w fazie o 90 stopni. Rozdzielczość pomiarowa jest określona przez liczbę impulsów przypadających na jeden obrót osi. Przykład takiego przebiegu pokazano na rysunku 10.
Najprostszym sposobem interpretacji jest traktowanie wyjścia A jako sygnału zegarowego, a wyjścia B jako informacji o kierunku. Wtedy na każdym narastającym zboczu sygnału A zmieniamy stan naszego licznika: jeżeli na wyjściu B panuje stan wysoki dodajemy, a jeżeli stan niski odejmujemy jedynkę. Musimy więc stworzyć kolejny moduł, którym jest…
Licznik dwukierunkowy
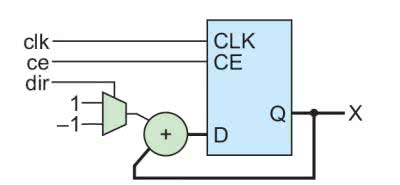
Schemat budowy licznika dwukierunkowego pokazuje rysunek 11. Jest bardzo podobny do wcześniejszej wersji licznika, ale posiada dodatkowe wejście dir. Steruje on multiplekserem, na którego wejściach są ustawione dwie stałe. Jeżeli na wejściu adresowym będzie stan wysoki, to na wejście bloku dodawania zostanie przekazana liczba 1, a jeżeli niski to –1.
Na listingu 5 pokazany jest fragment kodu, który realizuje logikę licznika.
20 always_ff @(posedge clk or negedge rst)
21 if (!rst)
22 q <= ‘0;
23 else if (ce)
24 q <= q + ((dir) ? 1’b1 : -1’b1);
Wybór kierunku został zrealizowany w linii 24 za pomocą trójargumentowego operatora ?:. Aby sprawdzić działanie tego modułu musimy w symulatorze ModelSim uruchomić skrypt:
Po zbudowaniu projektu możemy zaprogramować układ FPGA i przetestować jego działanie. Gdy obrócimy gałkę enkodera stan diod LED powinien ulec zmianie.
Podsumowanie
W tym odcinku uruchomiliśmy dwa proste projekty, które powinny nam pomóc zdobyć trochę intuicji odnośnie działania logiki cyfrowej. W następnym odcinku przejdziemy do ciekawszego zagadnienia – w końcu uruchomimy port szeregowy. A przy okazji zaznajomimy się z maszynami stanu.
Rafał Kozik
rafkozik@gmail.com
[1] Larson S., Debounce Logic Circuit http://bit.ly/2uFbMcJ

 Zaloguj
Zaloguj