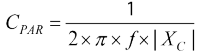Jest chyba zupełnie zrozumiałe, że każdy układ analogowy, który zasilany jest napięciem stałym, będzie działał inaczej, jeżeli na szynie zasilania pojawi się składowa zmienna. Ogromna większość układów analogowych – układy tranzystorowe, wzmacniacze operacyjne, komparatory oraz bardziej złożone struktury – zasilane są napięciem stałym i dla takiego napięcia podawane są parametry tych układów i specyfikowane jest ich zasilanie.
Niestety rzeczywistość, jak zwykle, jest bardziej skomplikowana niż symulacje i bardzo często w sygnale zasilania obecna jest składowa zmienna. Jej źródła mogą być bardzo różne – od systemów zasilania, które mogą niewystarczająco skutecznie blokować sygnały zmienne pochodzące z napięcia sieciowego (tętnienie o częstotliwości 100 Hz) lub z przetwornic impulsowych (o częstotliwości równej częstotliwości przełączania kluczy w układzie lub ich wyższych harmonicznych), aż po oznaki działania innych elementów w systemie, zwłaszcza elementów wysokiej mocy, które pobierając cyklicznie duże ilości prądu, mogą wywoływać silne zakłócenia w szynie zasilającej. Jest to szczególnie widoczne w przypadku systemów mieszanych, analogowo-cyfrowych, gdzie sekcja cyfrowa systemu pobiera duży prąd w takt zegara sterującego.
O tym, jak mocno wpływają zakłócenia w sieci zasilania na układy analogowe, mówi parametr PSRR, określany w ich kartach analogowych. Jest to Power Supply Rejection Rate, czyli współczynnik odrzucenia wpływu zasilania. Nie jest to zbyt wygodna do wymówienia nazwa, ale z pewnością dokładnie tłumaczy, czego dotyczy. Współczynnik PSRR jest miarą odrzucenia sygnału zmiennego zasilacza przez analizowany układ, wyrażoną, jako stosunek logarytmiczny szumu wyjściowego do szumu wejściowego zasilania. PSRR stanowi miarę tego, jak dobrze obwód tłumi tętnienia o różnych częstotliwościach wprowadzane na wejściu zasilającym. W przypadku elementów takich jak stabilizatory LDO, PSRR jest miarą tętnienia napięcia wyjściowego w porównaniu do tętnienia napięcia wejściowego.
Na równaniu 1 zaprezentowano wzór do jego wyznaczania. Parametr ten wyrażony jest w decybelach (dB) i na ogół podaje się go jako wartość dotyczącą szerokiego zakresu częstotliwości (typowo od 10 Hz do 1 MHz). PSRR jest bardzo krytycznym parametrem w wielu aplikacjach audio i RF.
gdzie:
ΔV – zmiana napięcia w czasie (amplituda), czyli składowa zmienna,
UZAS – napięcie zasilania,
UWY – napięcie wyjściowe układu.
Widać zatem, jak ważne jest filtrowanie składowej zmiennej z linii zasilania. Jednym z sposobów na filtrowanie zasilania jest umieszczenie w sygnale indukcyjności. Element indukcyjny wykazuje opór tym wyższy, im wyższa jest częstotliwość sygnału, co oznacza, że tłumi sygnały zmienne. Jednocześnie przepuszcza sygnały zasilania – dla napięcia stałego w zasadzie nie ma rezystancji (jest ona pomijalnie mała).
Tłumienie zakłóceń
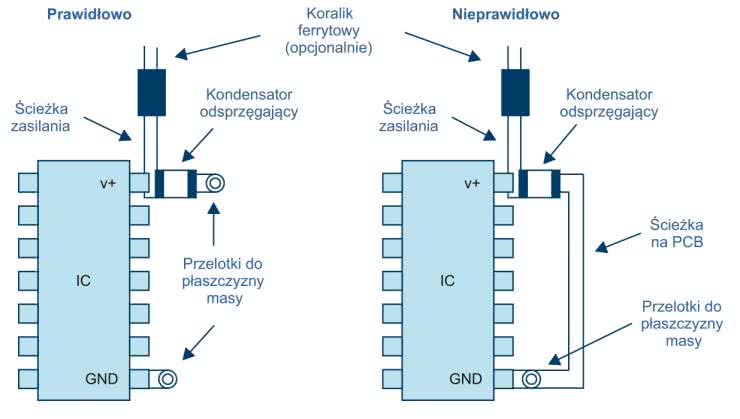
Filtrowanie szumów o niskiej częstotliwości zwykle wymaga kondensatorów elektrolitycznych (zazwyczaj o pojemności w zakresie od 1 μF do 100 μF), które działają jako magazyn ładunku dla prądów przejściowych o niskiej częstotliwości. Szum zasilania o wysokiej częstotliwości jest najlepiej redukowany za pomocą kondensatorów ceramicznych o niskiej indukcyjności, montowanych powierzchniowo, podłączonych bezpośrednio do styków zasilania układu scalonego (zwykle od 10 nF do 100 nF). Wszystkie kondensatory filtrujące muszą być podłączone bezpośrednio do wylewki masy o niskiej impedancji, aby skutecznie działały. Do tego połączenia wymagane są krótkie ścieżki lub przelotki, aby zminimalizować dodatkową indukcyjność szeregową ścieżek. Przykład takiego układu ścieżek pokazano na rysunku 1.
Można tam dostrzec jeszcze jeden element, który odpowiada za filtrowanie napięcia – koralik ferrytowy. Jest to prosty element indukcyjny, wykonany z fragmentu ferrytu (nieprzewodząca ceramika wytwarzana z tlenków niklu, cynku, manganu lub innych związków), który jest niesamowicie przydatny w filtrowaniu zasilania.
Koraliki ferrytowe
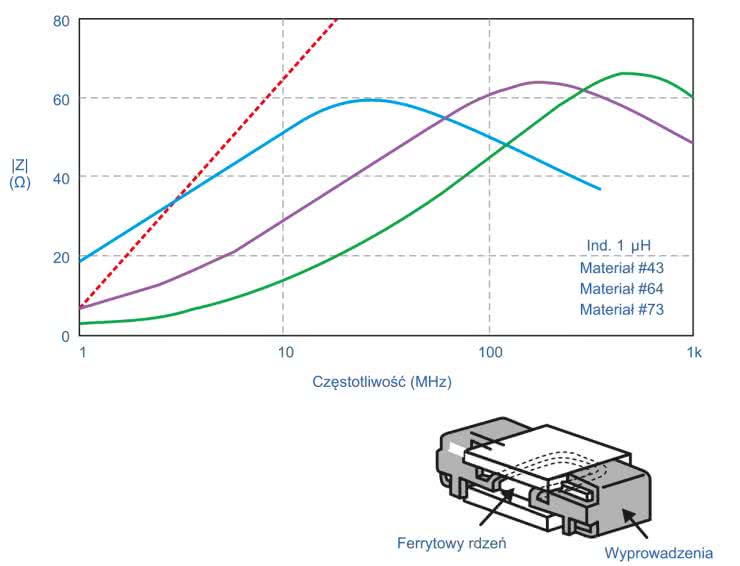
Przy niskich częstotliwościach (<100 kHz) ferryty mają charakter indukcyjny, dlatego są przydatne w dolnoprzepustowych filtrach filtrujących LC. Powyżej 100 kHz ferryty stają się głównie rezystancyjne (niskie Q). Impedancja ferrytu jest funkcją materiału, zakresu częstotliwości pracy, prądu polaryzacji stałoprądowej, liczby zwojów, rozmiaru, kształtu i temperatury. Przykładowy koralik ferrytowy SMD, wraz z przekrojem, pokazano na rysunku 2.
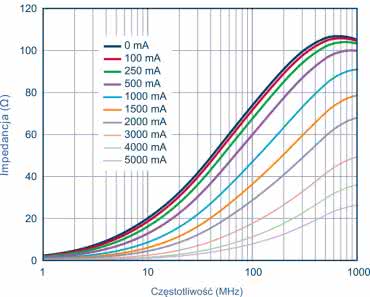
Koraliki ferrytowe nie zawsze są konieczne, ale zapewniają dodatkową izolację i filtrowanie zasilania od szumów o wysokiej częstotliwości, co jest często bardzo pożądane. Głównym problemem przy ich stosowaniu jest szansa ich nasycania, szczególnie w momencie, gdy zasilany układ pobiera spory prąd. Kiedy ferryt ulega nasyceniu, wtedy staje się nieliniowy i traci swoje właściwości filtrujące. Na rysunku 3 pokazano rodzinę krzywych – zależności impedancji od częstotliwości, dla tego samego elementu dla różnych prądów stałych, płynących przez element. Widać na nim, iż im wyższy prąd, tym impedancja jest niższa.
Indukcyjność a częstotliwość
Niektóre ferryty, nawet zanim nastąpi pełne nasycenie, mogą zachowywać się nieliniowo. Dlatego też, jeśli wymagany jest stopień mocy przystosowany do pracy z niskim poziomem zniekształceń wyjściowych, należy koralik sprawdzić w prototypie, zwłaszcza to, jak działa w pobliżu obszaru nasycenia. Typowy przebieg impedancji koralików ferrytowych pokazano na rysunku 2. Kształt tej krzywej zależny jest od materiału rdzenia – ferrytu – jaki zastosowano do konstrukcji koralika. Linią przerywaną pokazano zależność impedancji dla idealnej indukcyjności 1 μH.
Uproszczony model i symulacja koralików ferrytowych
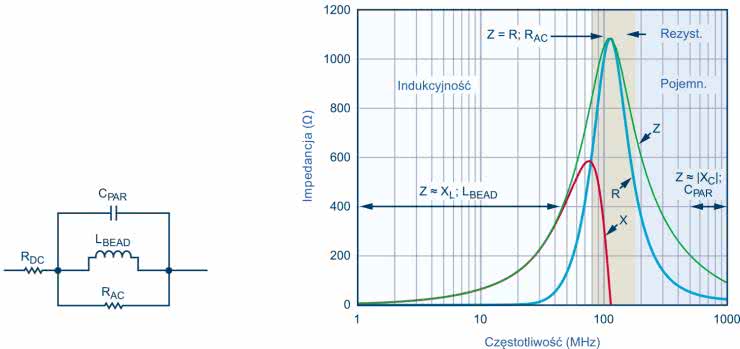
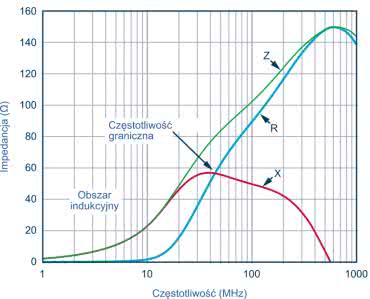
Koralik ferrytowy można modelować jako obwód składający się z rezystorów, cewki indukcyjnej i kondensatora, jak pokazano na schemacie z rysunku 4. Rezystancja RDC odpowiada rezystancji stałoprądowej. CPAR, LBEAD i RAC to, odpowiednio, pojemność pasożytnicza, indukcyjność koralika i rezystancja stałoprądowa – straty rdzenia w koraliku.
Charakterystyka koralika ferrytowego jest podzielona na trzy obszary odpowiedzi: indukcyjny, rezystancyjny i pojemnościowy. Regiony te można określić, patrząc na wykres Z, R i X (pokazane na rysunku 4), gdzie Z to impedancja, R to opór, a X to reaktancja koralika. Aby zredukować szum wysokiej częstości, koralik musi znajdować się w obszarze rezystancyjnym. Wtedy element ten działa jak rezystor, który tłumi szumy o wysokiej częstotliwości i rozprasza je w postaci ciepła. Obszar rezystancyjny występuje powyżej częstotliwości rozgraniczającej (gdzie X = R) i do momentu, w którym koralik przyjmuje charakter pojemnościowy. Ten punkt pojemnościowy występuje przy częstotliwości, w której bezwzględna wartość reaktancji (–X) jest równa rezystancji (–X = R).
W niektórych przypadkach uproszczony model obwodu można wykorzystać do przybliżenia charakterystyki impedancji koralików ferrytowych do zakresu poniżej GHz. Jako przykład użyto wielowarstwowego koralika ferrytowego Tyco Electronics BMB2A1000LN2.
Rysunek 4 pokazuje zmierzoną odpowiedź tego elementu dla zerowego prądu polaryzacji przy użyciu analizatora impedancji. Dla obszaru na zmierzonym wykresie, gdzie koralik wydaje się najbardziej indukcyjny (Z ≈ XL; dla L = LBEAD), indukcyjność koralika jest obliczana z następującego równania:
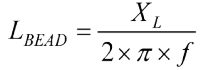
gdzie:
f – częstotliwość w obszarze indukcyjnym – np. 30,7 MHz dla tego elementu,
XL – reaktancja przy tej częstotliwości, która wynosi tutaj 233 Ω.
Z równania 2 wynika, że dla tego elementu LBEAD = 1,208 μH. Z obszaru, gdzie koralik wydaje się mieć własności bardziej pojemnościowe (Z ≈ |XC|; dla C = CPAR), pojemność pasożytnicza wyznaczana jest za pomocą równania 3.
gdzie f – częstotliwość w obszarze pojemnościowym, np. 803 MHz,
|XC| – reaktancja przy 803 MHz, która wynosi 118,1 Ω.
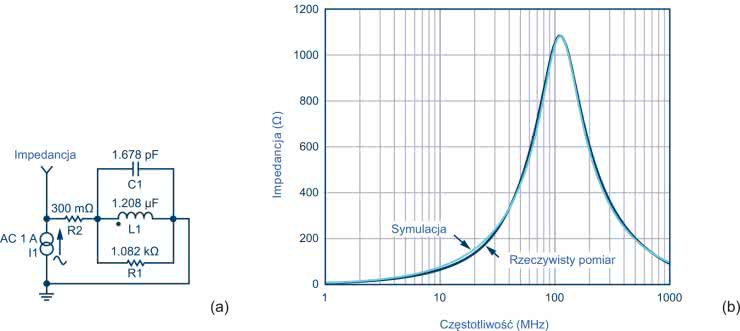
Równanie 2 daje wartość pojemności pasożytniczej CPAR = 1,678 pF. Rezystancję stałoprądową RDC, która wynosi 300 mΩ, można odczytać z karty katalogowej. Rezystancja dla prądu przemiennego RAC to szczytowa impedancja, przy której koralik wydaje się czysto rezystancyjny. Wartość RAC można obliczyć, odejmując RDC od zmierzonej wartości Z. Ponieważ RDC jest bardzo małe w porównaniu z impedancją szczytową, można ją pominąć. Dlatego w tym przypadku RAC wynosi 1,082 kΩ. Po uzyskaniu wszystkich wartości można podstawić je do modelu (rysunek 5), a następnie zasymulować je w dowolnym pakiecie. Wyniki takiej symulacji wykonane w ADIsimPE zaprezentowane są na charakterystyce z rysunku 5. Do wykresu dodano również przebieg zmierzonej krzywej, aby podkreślić wysoką zbieżność.
Efekt rezonansu LC
W przypadku zastosowania koralika ferrytowego wraz z kondensatorem filtrującym możliwe jest zaobserwowanie rezonansu w układzie LC. Ten często pomijany efekt może być szkodliwy, ponieważ może wzmacniać tętnienia i szumy w danym systemie, zamiast je tłumić. W wielu przypadkach szczyt ten występuje wokół popularnych częstotliwości przełączania przetwornic impulsowych w systemach zasilania.
Punkt szczytowy rezonansu występuje, gdy częstotliwość rezonansowa filtra dolnoprzepustowego, utworzonego przez indukcyjność koralika ferrytowego i pojemność kondensatora o wysokim współczynniku dobroci, jest niższa od częstotliwości granicznej tego koralika. Powstały filtr jest słabo tłumiony. Rysunek 6 pokazuje wykres zmierzonej impedancji w funkcji częstotliwości dla koralika TDK MPZ1608S101A.
Składnik rezystancyjny, od którego zależy rozproszenie niepożądanej energii, nie staje się istotny, aż do osiągnięcia zakresu od 20 MHz do 30 MHz. Poniżej tej częstotliwości koralik ferrytowy nadal ma bardzo wysokie Q i zachowuje się jak idealna cewka indukcyjna. Częstotliwości rezonansowe typowych filtrów LC tego typu mieszczą się na ogół w zakresie od 0,1 MHz do 10 MHz. W przypadku typowych częstotliwości tętnienia zasilania, będących w zakresie od 300 kHz do 5 MHz, wymagane jest dodatkowe tłumienie, aby zredukować dobroć Q filtra.
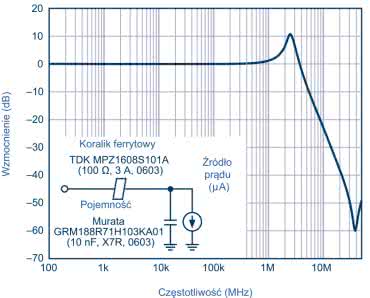
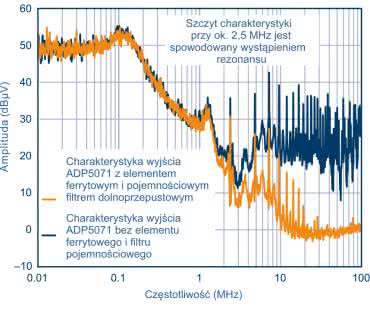
Jako przykład tego efektu rysunek 7 prezentuje odpowiedź częstotliwościową filtra dolnoprzepustowego zbudowanego z koralika i kondensatora. Na wykresie widać efekt szpilki. Zastosowany koralik ferrytowy to TDK MPZ1608S101A (100 Ω, 3 A, SMD0603), a kondensator to Murata GRM188R71H103KA01 o niskim ESR (10 nF, X7R, SMD0603). Prąd obciążenia podczas pomiaru mieści się w zakresie mikroamperów.
Nietłumiony filtr z koralików ferrytowych może wykazywać wartości szczytowe od około 10 dB do 15 dB wyższe, w zależności od dobroci Q obwodu filtra. Na rysunku 6 szczyt występuje przy około 2,5 MHz przy wzmocnieniu aż 10 dB. Dodatkowo widać wzmocnienie sygnału w zakresie od 1 MHz do 3,5 MHz. Ten wzrost jest problematyczny, jeśli występuje w paśmie częstotliwości, w którym działa np. stabilizator impulsowy. Wzmacnia to niepożądane artefakty przełączania, które mogą zakłócać wrażliwe elementy układu, takie jak pętla synchronizacji fazowej (PLL), oscylatory sterowane napięciem (VCO) czy przetworniki analogowo-cyfrowe o wysokiej rozdzielczości (ADC). Wynik pokazany na rysunku 6 został uzyskany przy bardzo małym obciążeniu, ale jest to realistyczne zastosowanie w sekcjach obwodów, które potrzebują tylko do 1 mA prądu. Ten rezonans zwiększa zakłócenia w całym systemie.
Przykład
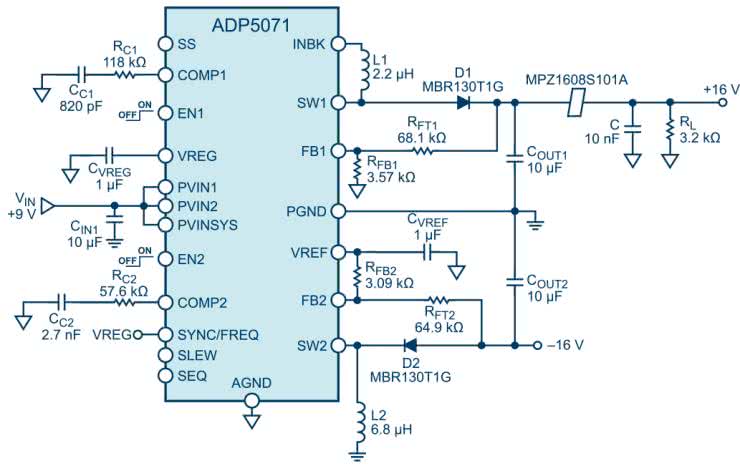
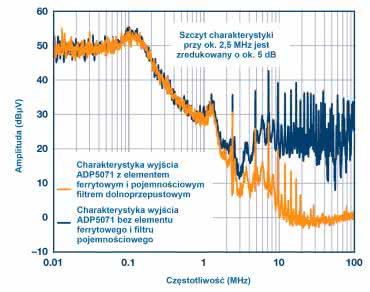
Na rysunku 8 zaprezentowano aplikację układu ADP5071 z zaimplementowanym filtrem z koralikiem ferrytowym, a rysunek 9 zawiera wykres widma sygnału na wyjściu dodatnim.
Częstotliwość przełączania jest ustawiona na 2,4 MHz, napięcie wejściowe 9 V, napięcie wyjściowe 16 V, a prąd obciążenia równy jest 5 mA. Szpilka rezonansowa występuje przy około 2,5 MHz ze względu na indukcyjność koralika i pojemność kondensatora ceramicznego 10 nF. Zamiast tłumienia tętnień przy 2,4 MHz występuje ich wzmocnienie o 10 dB!
Metody tłumienia
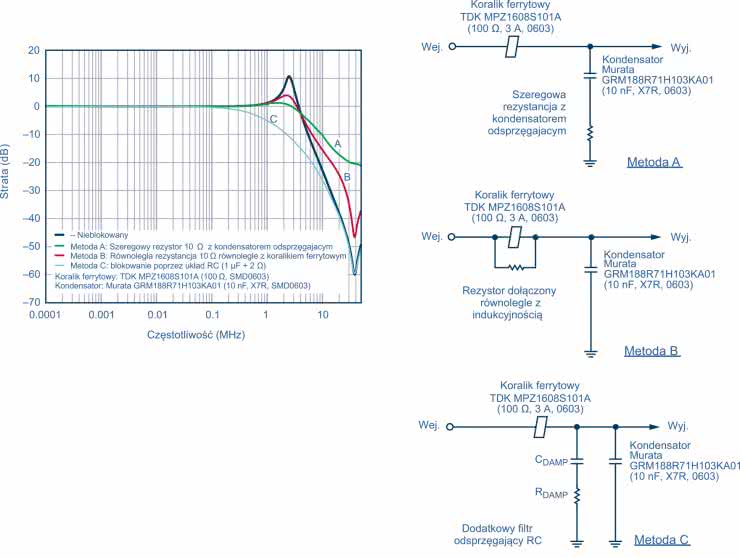
Poniżej opisano trzy metody tłumienia, które można zastosować w celu znacznego zmniejszenia poziomu wzmocnienia w zakresie rezonansu układu LC. Ich schematy oraz charakterystyki zostały pokazane na rysunku 10.
Metoda A
Pierwsza, najprostsza metoda polega na dodaniu rezystora szeregowego do kondensatora filtrującego, co tłumi rezonans systemu, ale równocześnie obniża skuteczność filtrowania sygnału, szczególnie przy wysokich częstotliwościach.
Metoda B
Druga metoda podobna jest do pierwszej i polega na dodaniu równoległego rezystora o niewielkim oporze do koralika ferrytowego, co również tłumi rezonans systemu. Jednak charakterystyka tłumienia takiego filtra jest również zmniejszona przy wysokich częstotliwościach.
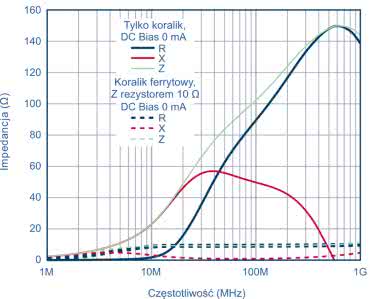
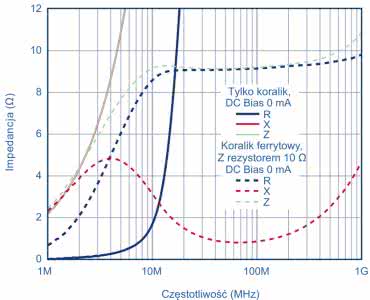
Na rysunkach 11 i 12 jest pokazana krzywa impedancji w funkcji częstotliwości dla przykładowego koralika MPZ1608S101A i bez rezystora równoległego 10 Ω. Jasnozielona krzywa przerywana to całkowita impedancja koralika z równoległym rezystorem 10 Ω.
Impedancja łączna koralika i rezystora jest znacznie zmniejszona i jest zdominowana przez rezystor 10 Ω. Jednak częstotliwość graniczna równa 3,8 MHz dla koralika z rezystorem równoległym 10 Ω jest znacznie niższa niż częstotliwość graniczna samego koralika – wypadająca przy 40,3 MHz. Koralik wydaje się rezystancyjny już w znacznie niższym zakresie częstotliwości, obniżając Q w celu poprawy tłumienia.
Metoda C
Ta metoda polega na dodaniu dużego kondensatora (CDAMP) z szeregowym rezystorem tłumiącym (RDAMP), co często jest optymalnym, ale niekoniecznie najprostszym rozwiązaniem. Dodanie tego kondensatora i rezystora tłumi rezonans systemu i nie obniża skuteczności filtrowania linii zasilania przy wysokich częstotliwościach. Zastosowanie tej metody pozwala uniknąć nadmiernego rozpraszania mocy na rezystorze z powodu dużego kondensatora filtrującego dla napięcia stałego. Kondensator musi być znacznie większy niż suma wszystkich kondensatorów filtrujących, co zmniejsza wymaganą wartość rezystora tłumiącego. Impedancja kondensatora musi być wystarczająco mniejsza niż rezystancja tłumienia przy częstotliwości rezonansowej, aby zredukować rezonans.
Rysunek 13 pokazuje wykres widmowy wyjścia dodatniego z ADP5071 z zaimplementowanym tłumieniem metodą C w obwodzie aplikacyjnym pokazanym na rysunku 8. Zastosowane CDAMP i RDAMP to odpowiednio kondensator ceramiczny 1 μF i rezystor 2 Ω SMD. Podstawowe tętnienie przy 2,4 MHz jest zmniejszone o 5 dB w przeciwieństwie do wzmocnienia 10 dB, pokazanego na rysunku 10.
Ogólnie rzecz biorąc, metoda C jest najbardziej efektywna i jest realizowana przez dodanie rezystora szeregowo z kondensatorem ceramicznym zamiast kupowania drogiego kondensatora tłumiącego. Charakteryzuje ją wysoki stosunek efektu do ceny, mimo najbardziej skomplikowanego obwodu. Najbezpieczniejsze projekty zawsze zawierają rezystor, który można modyfikować podczas prototypowania i który można wyeliminować, jeśli nie jest on konieczny. Jedyne wady takiego rozwiązania to dodatkowy koszt komponentów i większa wymagana przestrzeń na PCB.
Podsumowanie
W artykule omówiono kluczowe kwestie, które należy wziąć pod uwagę podczas korzystania z koralików ferrytowych do filtrowania zasilania. Szczegółowo prezentuje on również prosty model obwodu reprezentowanego przez koralik ferrytowy – wyniki symulacji pokazują dobrą korelację z rzeczywistą zmierzoną impedancją w stosunku do odpowiedzi częstotliwościowej przy zerowym prądzie polaryzacji DC. Wpływ ten został opisany, jednak bez szczegółowej analizy zjawiska nasycenia magnetycznego rdzenia, ponieważ wymagałoby to rozbudowanego, oddzielnego artykułu. Pokazano jednak, że prąd polaryzacji DC, większy niż 20% prądu znamionowego, może spowodować istotny spadek indukcyjności. Taki prąd może również zmniejszyć efektywną impedancję koralika i obniżyć jego zdolność do filtrowania zakłóceń.
Używając koralików ferrytowych na liniach zasilających, należy dobrać je do planowanego poboru prądu w układzie, aby prąd nie powodował nasycenia rdzenia i pracy w zakresie nieliniowym. Ponieważ koralik ferrytowy jest indukcyjny, nie należy go używać z kondensatorami filtrującymi o wysokim współczynniku dobroci bez starannej uwagi. Może to wyrządzić więcej szkody niż pożytku, powodując niepożądany rezonans w obwodzie. Metody tłumienia tego rezonansu, zaproponowane w tym artykule, oferują łatwe rozwiązanie dzięki zastosowaniu dużego kondensatora tłumiącego połączonego szeregowo z rezystorem, co pozwala uniknąć niepożądanego rezonansu. Prawidłowe zastosowanie koralików ferrytowych może być skutecznym i niedrogim sposobem na zmniejszenie szumów o wysokiej częstotliwości i stanów przejściowych przełączania w liniach zasilania i nie tylko.
Nikodem Czechowski, EP
Źródła:
- Sanjay Pithadia, Scot Lester, Ankur Verma, „LDO PSRR Measurement Simplified”, TI Application Report SLAA414A (2009, zaktualizowane 2017).
- Walt Kester, „Grounding and Decoupling: Learn Basics Now and Save Yourself Much Grief Later! Part 2: Decoupling”, Analog Dialogue 51 (kwiecień 2017).
- Aldrick Limjoco, Jefferson Eco, „Ferrite Beads Demystified”, Analog Dialogue 50 (luty 2016).

 Zaloguj
Zaloguj