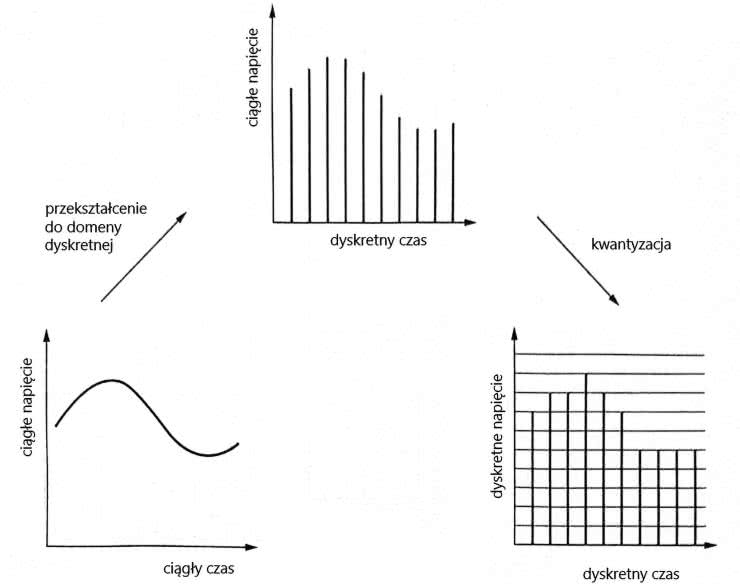
Jak już wiemy, analogowy sygnał jest konwertowany na postać cyfrową w procesie kwantowania. W wyniku konwersji otrzymujemy zbór liczb reprezentujących ten sygnał w domenie dyskretnej. Jeżeli kwantowanie (pobieranie próbek) zostało wykonane prawidłowo, czyli z częstotliwością spełniającą kryterium Nyquista, to ze zbioru próbek można odtworzyć sygnał analogowy bez utraty jakości. Dla przypomnienia na rysunku 1 pokazano proces kwantowania. Analogowy sygnał jest przekształcany do domeny cyfrowej poprzez mierzenie i zapisywanie wartości amplitudy napięcia z częstotliwością próbkowania Fs, czyli w jednakowych odstępach czasu równych 1/Fs. Zakładamy, że napięcie jest mierzone z nieskończoną rozdzielczością, czyli próbki mają charakter wartości analogowych. Kolejnym krokiem jest kwantyzacja, czyli zapisanie wartości owych próbek z określoną rozdzielczością bitową (na przykład 16 bitów).
Trzeba zwrócić uwagę na dwa ważne fakty, wynikające z dyskretnego przetwarzania sygnału. Po pierwsze pobieramy i zapisujemy próbki co zadany okres i tylko w tych momentach mamy informację o wartości próbkowanego sygnału. To, co się dzieje z sygnałem pomiędzy kolejnymi momentami próbkowania, nie zostanie zapisane i wydaje się, że jest bezpowrotnie tracone. Po drugie zarejestrowana amplituda sygnału po procesie kwantowania będzie, z dużym prawdopodobieństwem, różnić się od rzeczywistej wartości sygnału mierzonego w momentach następujących co 1/Fs. Proces kwantyzacji napięcia musi nieuchronnie prowadzić do powstania zniekształceń amplitudy odtworzonej na podstawie tak zapisanych próbek. Jak zobaczymy dalej, nie musi to jednak być tożsame z modyfikacją kształtu sygnału, czyli wprowadzaniem zniekształceń harmonicznych.
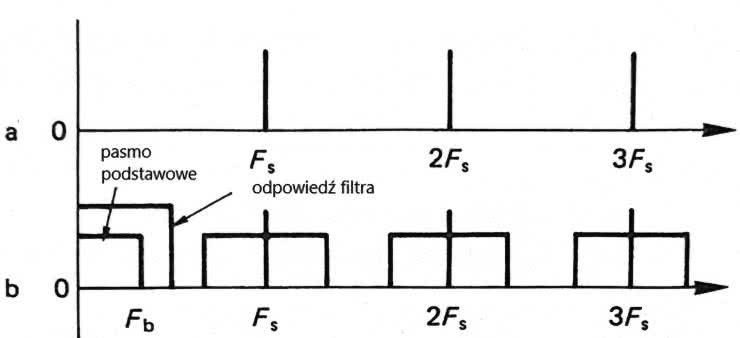
Kwantyzacja jest odpowiednikiem stosowanej w radiofonii modulacji amplitudy (AM). Ciąg impulsów o stałej amplitudzie (nośna), pojawiających się w odstępach czasowych równych 1/Fs, jest modulowany wartością próbek odczytywanych z zapisanego zbioru (sygnał modulujący). Podobnie jak radiowa modulacja AM, proces ten wytwarza pasma boczne powyżej i poniżej nośnej. Innymi słowy, próbkowanie również wytwarza pasma boczne, chociaż nośna jest teraz ciągiem impulsów i ma nieskończoną ilość harmonicznych, jak pokazano na rysunku 2a. Pasma boczne powtarzają się powyżej i poniżej każdej harmonicznej częstotliwości próbkowania, co widać na rysunku 2b.
Pasmo podstawowe zawiera widmo sygnału kwantowanego i ma szerokość od 0 Hz do Fb, gdzie Fb to maksymalna częstotliwość sygnału kwantowanego.
Opisane zjawiska powstają w procesie kwantyzacji, czyli konwersji analogowo-cyfrowej. Proces odwrotny, czyli konwersja cyfrowo-analogowa, ma za zadanie odtworzyć z zapisanych próbek oryginalny sygnał analogowy.
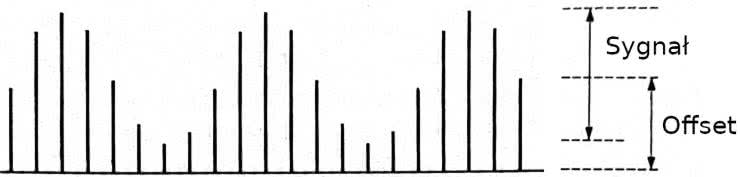
Zastanówmy się, jak mógłby wyglądać proces konwersji cyfrowo-analogowej. Wyobraźmy sobie urządzenie (przetwornik), które z pliku pobiera liczbę odpowiadającą amplitudzie skwantowanego sygnału. Na podstawie jej wartości przetwornik wystawia na wyjściu impulsy co 1/Fs o zerowym czasie trwania i napięciu proporcjonalnym do napięcia odniesienia (czyli napięcia pełnego zakresu). Odpowiadają one próbkom pobranym w procesie kwantowania sygnału. Wynik mógłby wyglądać tak, jak na rysunku 3. Ponieważ próbki są zapisywane jako liczby całkowite bez znaku, to dodaje się do nich stały offset o wartości równej połowie ich maksymalnej amplitudy.
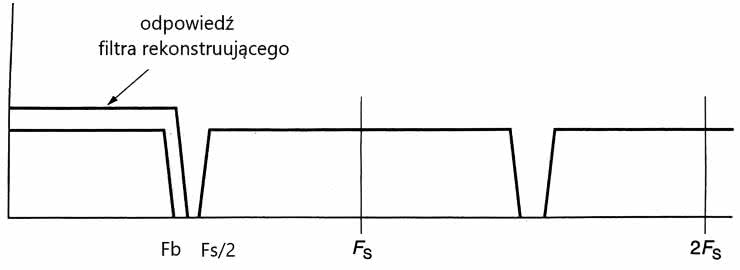
Na początek załóżmy, że mamy na wyjściu przetwornika ciąg idealnych impulsów – takich, jak na rysunku 3. Jak już wiemy, ich widmo zawiera pasmo podstawowe od 0 Hz do Fb i powielone pasma z wstęgami bocznymi o szerokości równej wartości Fs, układającymi się symetrycznie wokół wielokrotności częstotliwości próbkowania Fs (rysunek 4). Można się spodziewać, że po konwersji tego ciągu impulsów na sygnał analogowy będzie on zawierał pasmo podstawowe i powielone pasma – podobnie, jak na rysunku 2b. Proces kwantyzacji powoduje zatem powielanie pasma w domenie cyfrowej, czyli próbki zawierają – oprócz skwantowanego pasma – „matematyczną” informację o jego powielonych kopiach. Niestety po konwersji odwrotnej te powielone pasma z domeny cyfrowej pojawiają się w rzeczywistym sygnale analogowym. W prawidłowo skwantowanym sygnale (bez aliasingu) te znajdują się one poza pasmem akustycznym (obejmującym zakres od 0 Hz do Fb) i w praktyce powinniśmy się ich bez problemu pozbyć. Jest na to prosty sposób – filtrowanie dolnoprzepustowe. Na początek poddamy zatem to pasmo idealnemu, analogowemu filtrowaniu dolnoprzepustowemu. Filtr powinien przenosić bez zmian wszystkie częstotliwości od 0 Hz do Fs/2 i całkowicie tłumić częstotliwości powyżej Fs/2. Wyniku filtrowania mamy wyodrębnione pasmo podstawowe od 0 Hz do Fs/2. Wszystkie wstęgi powielonego pasma, tak jak chcieliśmy, zostały idealnie odfiltrowane (stłumione).
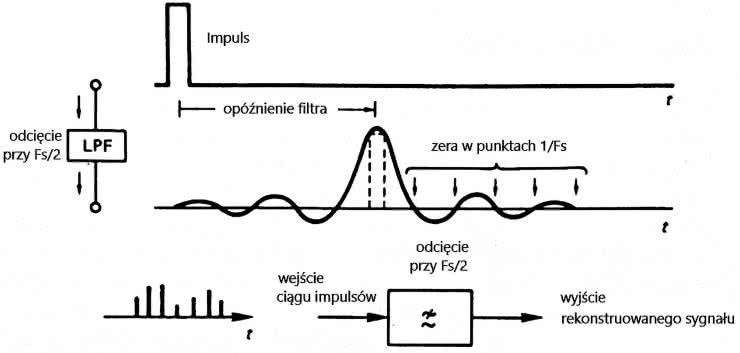
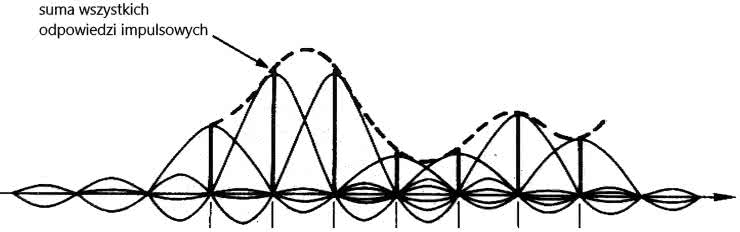
Wróćmy do rysunku 3. Każdy z impulsów na wyjściu przetwornika jest poddawany działaniu tego filtra dolnoprzepustowego. Odpowiedź impulsowa liniowego fazowo, idealnego, dolnoprzepustowego filtra na takie pobudzenie jest zgodna z funkcją sin(x)/x (w dziedzinie czasu). Inaczej mówiąc: jeżeli na wejście idealnego filtra dolnoprzepustowego podamy impuls o pomijalnym czasie trwania, to na jego wyjściu otrzymamy przebieg odpowiadający funkcji sin(x)/x. To jednak nie wszystko. Przebieg sin(x)/x przechodzi przez wartości zerowe w odległościach 1/Fs. Dlatego odpowiedź impulsowa wywołana opisywanym pobudzeniem nie wpływa na odpowiedzi impulsowe filtra dla kolejnych próbek, pojawiających się co czas 1/Fs. Ta bardzo ważna właściwość została zobrazowana na rysunku 5.
Jeżeli teraz podamy na wejście idealnego filtra dolnoprzepustowego ciąg impulsów z wyjścia przetwornika, to przebiegi sin(x)/x na wyjściu filtra będą tworzyły obwiednię, zbudowaną z sumy odpowiedzi impulsowych na impulsy reprezentujące kolejne próbki i odtwarzającą próbkowany przebieg bez zniekształceń – rysunek 6.
Dyskretny sygnał, reprezentowany przez próbki pobierane z częstotliwością Fs, jest przekształcany do postaci ciągłej w dziedzinie czasu poprzez filtrowanie impulsów wyjściowych przetwornika filtrem dolnoprzepustowym. Filtr ten musi przenosić bez zmian pasmo podstawowe do częstotliwości Fs/2, a tłumić wszystkie pasma powielone powyżej Fs/2. Taki układ spełnia rolę filtra rekonstruującego.
Jeżeli filtr dolnoprzepustowy ma pionowo opadającą charakterystykę przy częstotliwości Fs/2, to analogowy sygnał na jego wyjściu ma płaskie pasmo równe pasmu sygnału próbkowanego.
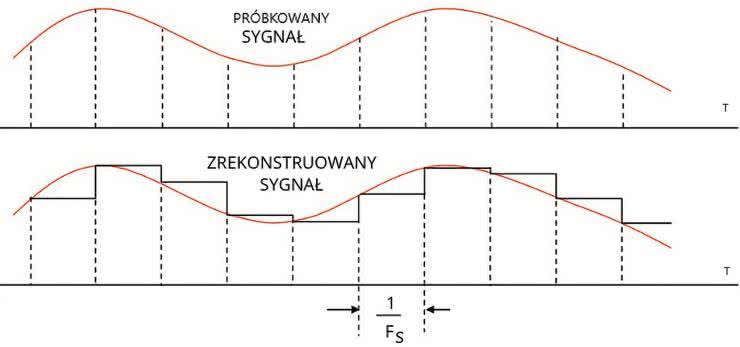
Popatrzmy teraz jak to wygląda w praktyce. Teoria zakłada, że na wyjściu przetwornika mamy ciąg idealnych impulsów o pomijalnym czasie trwania. W rzeczywistym świecie nie można wygenerować takich impulsów, które miałyby pomijalny czas trwania i zerowe czasy narastania oraz opadania. Rzeczywiste przetworniki nie działają w ten sposób. Napięcie na ich wyjściu utrzymuje stałą wartość przez praktycznie cały okres równy 1/Fs. Powoduje to, że sygnał wyjściowy przypomina przebieg schodkowy, a nie ciąg impulsów (rysunek 7). Taki system generowania napięcia nazywa się systemem zerowego rzędu z aperturą (wypełnieniem) 100%.
Jak się łatwo domyśleć, taka konwersja nie spełnia założeń teoretycznych opisanych powyżej i analogowy sygnał wyjściowy – po przejściu przez filtr rekonstruujący – musi być w jakiś sposób modyfikowany.
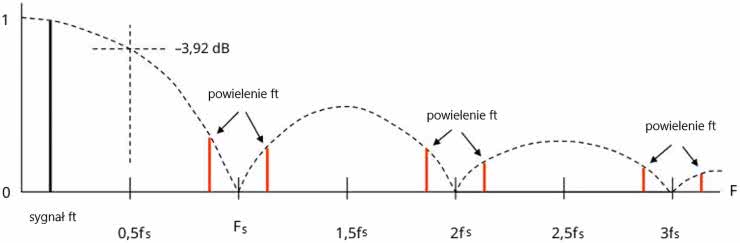
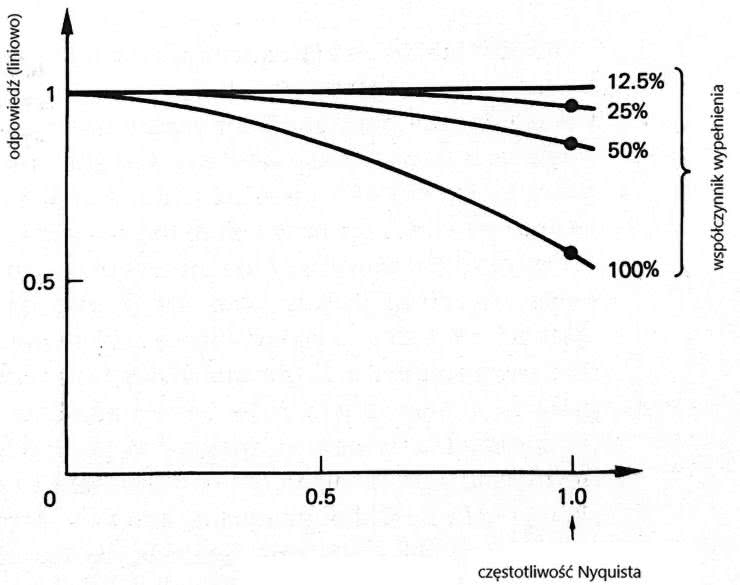
Na szczęście zmiana dotyczy tylko charakterystyki amplitudowo-częstotliwościowej, a nie kształtu sygnału (co wiązałoby się z pojawieniem zniekształceń harmonicznych). Jak już wspomniałem, w teoretycznie idealnych warunkach pasmo sygnału wyjściowego jest płaskie i równe pasmu próbkowanego sygnału. Charakterystyka amplitudowo-częstotliwościowa przebiegu schodkowego (pokazanego na rysunku 7 przebiega zgodnie z funkcją sin(x)/x. Pokazano to na rysunku 8.
Jak widać, przy częstotliwości Fs/2 amplituda spada o –3,92 dB w stosunku do początku pasma. Przy częstotliwości Fs i jej wielokrotnościach amplituda ma wartość zerową. Jeśli szerokość przebiegu schodkowego na wyjściu jest stabilna, to redukcja powielonych wysokich częstotliwości ponadakustycznych jest przewidywalna. Odpowiednio dobrany obwód korekcyjny, na przykład w postaci odwrotnego filtra sin(x)/x, może spowodować że charakterystyka stanie ponownie się płaska.
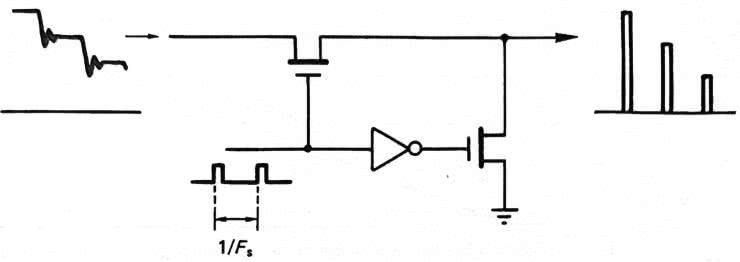
Innym środkiem zaradczym jest resampling, polegający na przekształcaniu sygnału schodkowego z rysunku 6 na ciąg impulsów o wypełnieniu (aperturze) poniżej 100%. Na rysunku 9 pokazano ideę układu resamplingu, zamieniającego przebieg schodkowy w ciąg impulsów o niższej aperturze.
Przy zmniejszeniu apertury do wartości 50% charakterystyka częstotliwościowa staje się bardziej płaska. Praktycznym limitem jest 12,5%, kiedy charakterystyka jest już w praktyce akceptowalna – rysunek 10. Dalsze zmniejszanie apertury nie jest właściwe, bo powoduje problemy z szumem sygnału wyjściowego.
Należy zwrócić uwagę, że terminem resampling nazywa się również proces zmiany częstotliwości próbkowania i należy te dwa pojęcia rozróżniać zależnie od kontekstu.
Kolejnym idealnym elementem, który nie może być zrealizowany w praktyce, jest filtr dolnoprzepustowy o pionowej charakterystyce opadania. Taki filtr musiałby mieć nieskończony czas opóźnienia. Musimy się więc pogodzić, że charakterystyka filtra rekonstruującego będzie miała określone nachylenie i filtrowanie takie, jak pokazano na rysunku 4 (w którym idealnie przenoszone jest pasmo do częstotliwości Fs/2 i idealnie tłumione powyżej Fs/2) nie będzie wykonalne. Oznacza to, że pasmo sygnału audio musi mieć niższą częstotliwość graniczną Fb w porównaniu do Fs/2. Dlatego w standardzie CD pasmo przenoszenia wynosi 20 kHz, a częstotliwość próbkowania Fs=44,1 kHz – a zatem Fs/2=22,05 kHz. Wtedy można zaprojektować filtr, który będzie przenosił 20 kHz i wystarczająco tłumił częstotliwości powyżej Fs/2=22,05 kHz.
Filtr rekonstruujący realizuje dwa zadania: oprócz odtwarzania sygnału analogowego z ciągu impulsów (lub sygnału schodkowego) spełnia również funkcję filtrowania sygnału wyjściowego z częstotliwości ponadakustycznych powielanego pasma.
Nadpróbkowanie (oversampling)
W procesie konwersji sygnału analogowego na postać cyfrową (i odwrotnie) stosuje się pewne techniki pozwalające na uproszczenie tych procesów i poprawę parametrów konwertowanych sygnałów. Jedną z najczęściej używanych metod jest nadpróbkowanie.
Jak już wiemy, nadpróbkowanie oznacza użycie częstotliwości próbkowania, która jest większa (zwykle wielokrotnie) niż częstotliwość Nyquista, wynikająca z pasma sygnału próbkowanego. Ani teoria próbkowania, ani teoria kwantyzacji, nie wymagają nadpróbkowania, aby uzyskać pożądaną jakość sygnału. Jak wiemy, można ją uzyskać stosując wystarczające próbkowanie, zgodnie z kryterium Nyquista. Ale kryterium Nyquista nakłada wysokie wymagania na budowę analogowego filtra rekonstruującego w konwersji cyfrowo-analogowej. Analogicznie jest w przypadku konwersji analogowo-cyfrowej, w której wysokie wymagania musi spełniać filtr antyaliasingowy.
W przykładzie standardu CD analogowy filtr rekonstruujący powinien przenosić bez zmian sygnał od 0 Hz do 20 kHz i tłumić całkowicie (a w praktyce: odpowiednio mocno) sygnały o częstotliwości 22,1 kHz (rysunek 11). Wykonanie takiego filtra jest technicznie możliwe, ale wymaga to stosowania elementów o nietypowych wartościach i niskich tolerancjach, co jest kłopotliwe i drogie.
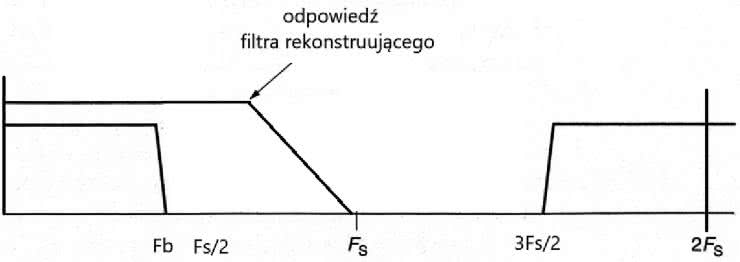
W przypadku konwersji cyfrowo-analogowej możemy sobie wyobrazić sytuację, w której próbki pobrane z częstotliwością dwukrotnie większą niż wynikająca z kryterium Nyquista, czyli 2Fs=88,2 kHz, dalej reprezentują analogowy sygnał audio o paśmie rozciągającym się od 0 Hz do Fb=20 kHz. Wstęga dolna pierwszego powielonego pasma nie będzie się zaczynała od Fs/2, czyli 44,1 kHz/2=22,05 kHz, tylko od 3Fs/2=66,15 kHz.
Rysunek 12 prezentuje jedną z zalet nadpróbkowania. Zastoso-wanie częstotliwości próbkowania znacznie przekraczającej częstotliwość Nyquista pozwala na realizację filtra rekonstrukcyjnego z dużo łagodniejszym nachyleniem odcięcia. Istnieje wówczas znacznie mniejsze prawdopodobieństwo wystąpienia problemów z liniowością fazy i zafalowaniami charakterystyki w paśmie sygnału audio do częstotliwości Fb.
W praktyce stosuje się nadpróbkowania 4-krotne lub 8-krotne, co jeszcze bardziej łagodzi wymagania odnośnie charakterystyki i tym samym dodatkowo upraszcza realizację filtra dolnoprzepustowego.
Jeśli współczynnik nadpróbkowania wynosi n, to wejściowe pasmo analogowe musi być ograniczone do nFs/2 przez analogowy filtr rekonstruujący, który musi zachować płaską odpowiedź częstotliwościową i liniowość fazy jedynie w paśmie audio.
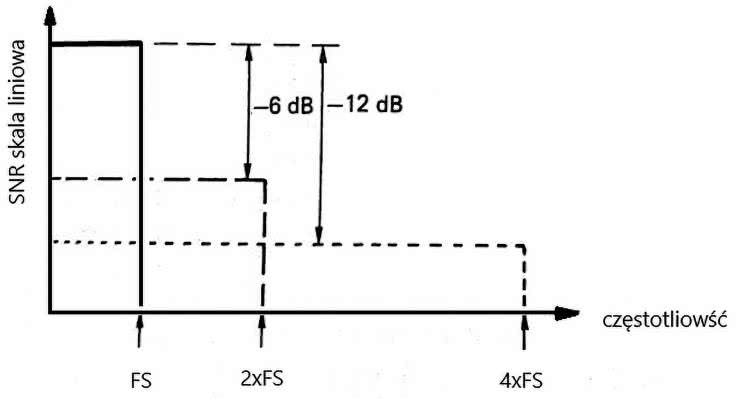
Informacje przesyłane w kanale analogowym można opisać jako obszar, który jest iloczynem szerokości pasma i liniowo wyrażonego stosunku sygnału do szumu (SNR) – patrz rysunek 13. Jeżeli przy tej samej ilości przesyłanej informacji w kanale będziemy zwiększać szerokość pasma, to wartość SNR będzie malała. Dwukrotne zwiększenie pasma powoduje teoretyczne poszerzenie SNR o 6 dB, czterokrotne zwiększenie pasma powoduje poszerzenie SNR o 12 dB i tak dalej. W naszym przypadku szerokość pasma jest określana przez częstotliwość próbkowania Fs. Teoretycznie przy Fs=44,1 kHz szerokość pasma jest równa 22,05 kHz, ale przy częstotliwości próbkowania 2Fs=88,2 kHz szerokość pasma to 44,1 kHz. Moc szumu rozciąga się na całe pasmo podstawowe, aż do granicy Nyquista. W procesie nadpróbkowania szerokość pasma rośnie wraz ze współczynnikiem nadpróbkowania n i jest równa n·FS.
Jeśli teraz szerokość pasma podstawowego zostanie zmniejszona o współczynnik nadpróbkowania wynoszący na przykład cztery, z powrotem do oryginalnego pasma analogowego (przez cyfrowy filtr FIR interpolatora), to pasmo szumu zostanie zmniejszone czterokrotnie, a moc szumu będzie stanowić jedną czwartą mocy wytwarzanej przez kwantyzator. Jedna czwarta mocy szumu oznacza z kolei o połowę niższe napięcie szumu, więc SNR w tym przykładzie został zwiększony o 6 dB.
Nadpróbkowanie powoduje redukcję szumów konwertera, bo określona część energii szumów pozostaje poza pasmem akustycznym.
Podany tu przykład redukcji szumów jest prawdziwy dla idealnego konwertera próbkującego sygnał szumu białego o jednolitej gęstości widmowej. Jeśli szum z kwantyzatora stanie się widmowo niejednolity, współczynnik nadpróbkowania nie będzie już czynnikiem zmniejszającym moc szumu o 6 dB przy dwukrotnym zwiększeniu Fs.
Żeby osiągnąć znaczącą redukcję szumów, w metodzie nadpróbkowania stosuje się technikę kształtowania szumów (noise shaping). Jej celem jest skoncentrowanie mocy szumu na wysokich częstotliwościach, tak aby po filtrowaniu dolnoprzepustowym w domenie cyfrowej, aż do szerokości pasma wejściowego, audio moc szumu została zmniejszona o więcej niż współczynnik nadpróbkowania. Jest to technika sprzężenia zwrotnego stosowana w kwantyzatorach i rekwantyzatorach, w której proces kwantyzacji bieżącej próbki jest w pewien sposób modyfikowany przez błąd kwantyzacji poprzedniej próbki.
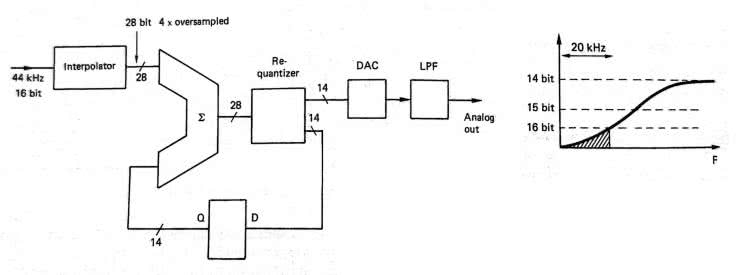
Przykładową technikę kształtowania szumu zastosowano w odtwarzaczach CD firmy Philips pierwszej generacji, które zapewniały czterokrotne nadpróbkowanie. Idea tego rozwiązania polegała na tym, by wejściowe dane z płyty CD o długości 16 bitów i Fs=44,1 kHz były konwertowane przy użyciu 14-bitowego przetwornika. Zmniejszenie długości słowa o 2 bity zwiększa poziom szumów kwantyzacji, co jest następnie korygowane przez układ kształtowania szumów.
Opisywany system DAC z nadpróbkowaniem pokazano na rysunku 14. Proces nadpróbkowania wykonywany w filtrze interpolatora (jego działanie jest wyjaśnione poniżej) powoduje 4-krotne zwiększenie częstotliwości próbkowania i wydłużenie słowa do 28 bitów poprzez arytmetyczne operacje na 16-bitowym słowie danych.
Dane o długości 28 bitów trafiają na układ sprzężenia zwrotnego, który rozdziela je na 14-bitowy sygnał do konwersji DAC i 14 bitowy sygnał sprzężenia zwrotnego. Ten ostatni jest opóźniany o jeden takt zegara w przerzutnikach typu D umieszczonych w torze sprzężenia. Sygnał z poprzedniej próbki jest sumowany z sygnałem bieżącej próbki. Poziom szumów nieznacznie wzrasta w kierunku krawędzi pasma audio, ale pozostaje poniżej poziomu szumów konwencjonalnego, szesnastobitowego przetwornika DAC. Na rysunku 14 pokazano także wykres wyniku działania techniki kształtowania szumów – w paśmie akustycznym jest on porównywalny do szumów przetwornika 16-bitowego. Po co tak komplikować całość? Najprawdopodobniej dużo łatwiej w tamtym czasie było technologicznie wykonać konwerter 14-bitowy (o dobrych parametrach) niż 16-bitowy. Użyta technika pozwalała dorównać parametrom osiąganym przez 16-bitowe przetworniki. Ale nic nie stoi na przeszkodzie, by uzyskać w ten sposób parametry przetwarzania 18-bitowego przy konwerterze 16 bitowym.
Jak już powiedzieliśmy, informacje w sygnale analogowym mogą być przekazywane przy użyciu pewnego schematu modulacji analogowej, w dowolnej kombinacji szerokości pasma i SNR, która zapewnia odpowiednią pojemność kanału. Jeśli szerokość pasma zostanie zastąpiona częstotliwością próbkowania, a SNR – funkcją długości słowa – to… to samo musi dotyczyć sygnału cyfrowego, ponieważ jest on niczym więcej, niż tylko analogiem numerycznym. Dlatego zwiększenie częstotliwości próbkowania potencjalnie pozwala na zmniejszenie długości słowa każdej próbki bez utraty informacji.
Inaczej mówiąc możemy zmniejszać długość słowa przy jednoczesnym zwiększaniu częstotliwości próbkowania i na odwrót.
Sygnał audio można próbkować z wielokrotnością częstotliwości wynikającej z kryterium Nyquista i w takiej postaci go zapisywać oraz przesyłać. Dzisiaj są dostępne formaty zwane „gęstymi” o długości słowa równej 24 bity i częstotliwości próbkowania 96 kHz lub nawet 192 kHz, reprezentujące sygnał analogowy o paśmie 0…20 kHz. Mają one mieć możliwość przesyłania muzyki o dużo wyższej jakości niż tradycyjny format CD 16/44,1. A skoro istnieją takie możliwości techniczne i widoczne zapotrzebowanie „społeczne”, to formaty gęste są oferowane i dostępne. O ile zwiększenie długości słowa można uznać za zaletę (bo im większa długość, tym mniejszy szum kwantyzacji), to nadpróbkowane dane na wejściu przetwornika teoretycznie są zupełnie nadmiarowe i niczego nie zmieniają. Ten sam efekt można uzyskać przez nadpróbkowanie sygnału wejściowego w filtrze interpolatora przetwornika.
W klasycznym przetworniku pozbawionym nadpróbkowania strumień danych wejściowych (na przykład z odtwarzacza CD 16 bitów/44,1 kHz) jest podawany bezpośrednio na konwerter cyfra/napięcie, potem poddawany ewentualnemu procesowi resamplingu (żeby zmniejszyć współczynnik apertury – patrz rysunki 9 i 10) i dalej filtrowany przez analogowy filtr rekonstruujący – rysunek 15.
Jak wiemy, filtr rekonstruujący musi spełniać surowe wymagania pod względem tłumienia poza pasmem akustycznym, żeby móc odfiltrować powielone pasma zaczynające się już od Fs/2.
Jeżeli na wejście trafi strumień danych próbkowany zgodnie z kryterium Nyquista, to nadpróbkowanie trzeba wykonać w układzie przetwornika. Jak to zrobić?
Konwersję częstotliwości próbkowania można przeprowadzić powracając do domeny analogowej. Przetwornik cyfrowo-analogowy jest podłączony do przetwornika analogowo-cyfrowego. Aby spełnić wymagania teorii próbkowania, między nimi musi znajdować się filtr dolnoprzepustowy o charakterystyce częstotliwości ograniczonej do połowy niższej częstotliwości próbkowania. W rzeczywistości rzadko się to robi, ponieważ niezbędne stosowanie filtrów analogowych (rekonstruującego i antyaliasingowego) wprowadza zniekształcenia, szczególnie fazowe.
Preferowane są metody konwersji częstotliwości próbkowania w domenie cyfrowej. Nadpróbkowanie stosowane w konwersji cyfrowo-analogowej polega na zwiększaniu częstotliwości próbkowania o czynnik całkowity. Wtedy dodatkowe próbki muszą zostać utworzone w równych odstępach między istniejącymi. Nie ma potrzeby zmniejszania szerokości pasma próbek wejściowych, ponieważ jeśli oryginalna częstotliwość próbkowania była odpowiednia, to wyższa również musi być odpowiednia.
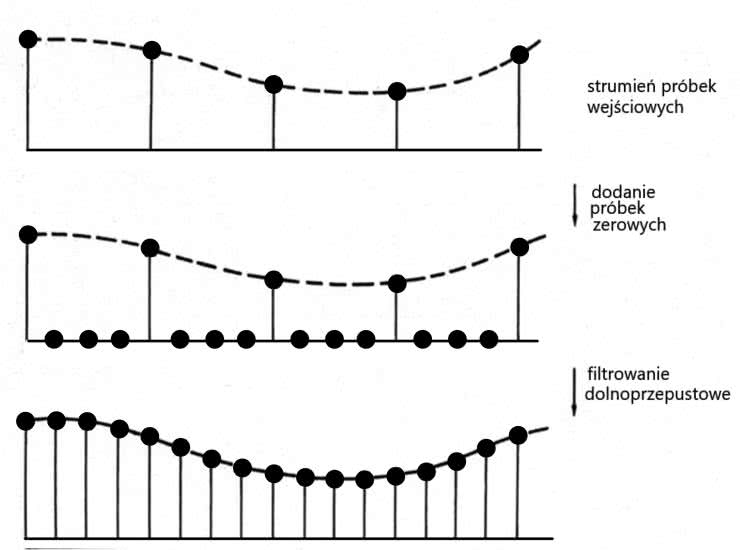
Proces zwiększania częstotliwości próbkowania można rozpatrywać w dwóch etapach. Najpierw uzyskuje się właściwą częstotliwość, wstawiając próbki o wartości zerowej w odpowiednich momentach pomiędzy istniejącymi próbkami, a następnie dodatkowym próbkom nadaje się znaczące wartości, przepuszczając strumień przez cyfrowy filtr dolnoprzepustowy odcinający sygnały się przy częstotliwości Nyquista określonej względem oryginalnej częstotliwości próbkowania – rysunek 16. Filtr ten nazywany jest filtrem interpolatora, a kolejnym z jego zadań jest zapobieganie pojawianiu się powielonych pasm, pochodzących z niższego widma próbkowania wejściowego, w rozszerzonym paśmie podstawowym widma wyjściowego (o wyższej częstotliwości).
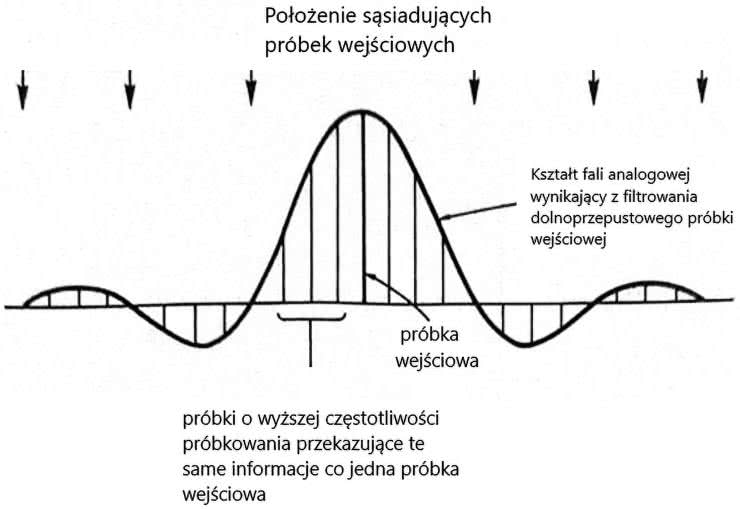
Jak działają interpolatory? Ważne jest, aby zdać sobie sprawę, że zgodnie z teorią próbkowania wszystkie próbkowane sygnały mają skończoną szerokość pasma (są dolnopasmowe). Wartość próbki cyfrowej jest uzyskiwana poprzez próbkowanie (mierzenie) chwilowego napięcia oryginalnego analogowego sygnału. Ponieważ impuls reprezentujący próbkę ma zerowy czas trwania, to musi mieć także zerowe czasy narastania i opadania – a przez to reprezentuje w domenie częstotliwości nieskończone widmo. Jednak taka próbka podlega procesowi rekonstrukcji, który ogranicza widmo impulsu do granicy Nyquista. Jak już wiemy, po rekonstrukcji jedna (nieskończenie krótka) próbka cyfrowa reprezentuje impuls sin(x)/x, którego centralna szerokość szczytu jest określana przez odpowiedź filtra rekonstrukcji, a amplituda jest proporcjonalna do wartości próbki. Oznacza to, że w rzeczywistości jedna wartość próbki ma znaczenie w szerszym przedziale czasowym, a nie tylko w chwili odpowiadającej próbce – tak jak to zostało pokazane na rysunku 5. Gdyby nie to, zbudowanie interpolatora byłoby niemożliwe.
Kiedy częstotliwość próbkowania jest zwiększana, szerokość pasma sygnału pozostaje niezmieniona; dlatego oryginalne próbki wejściowe przejdą przez filtr bez zmian, zbędne jest zatem ich obliczanie.
W przetworniku z nadpróbkowaniem wejściowy strumień danych trafia najpierw do bloku interpolatora, który – jak wiemy – zwiększa ilość próbek na wyjściu, a tym samym umożliwia podwyższenie częstotliwości próbkowania. Popatrzmy na rysunek 17.
Pojedyncza próbka, po filtrowaniu w domenie analogowej, daje przebieg sin(x)/x. Przy nowej, wyższej częstotliwości próbkowania, ten przebieg się nie zmieni i będzie zawierał nowo dodane próbki o wyższej częstotliwości. Wartość tych nowych próbek można obliczyć z próbek wejściowych w domenie cyfrowej, filtrując je dolnoprzepustowo w filtrze FIR – tak jak to pokazano na rysunku 16. Proces interpolacji jest w zasadzie taki sam, jak filtrowanie rekonstrukcyjne, które ma miejsce w przetwornikach cyfrowo-analogowych. W cyfrowym filtrze interpolacyjnym proces ten jest powielany, ale w domenie dyskretnej.
Szum, czyli błąd kwantyzacji
Wspomnieliśmy już o szumie kwantyzacji w rozważaniach o nadpróbkowaniu. Do jego redukcji w przetwornikach cyfrowo-analogowych stosuje się nadpróbkowanie połączone z mechanizmem kształtowania szumu (noise shsping). Popatrzmy teraz, jaka jest natura tego zjawiska i jakie niesie ono ze sobą zagrożenia dla wierności rejestracji i odtwarzania sygnału analogowego.
Szum kwantyzacji – a ściśle rzecz ujmując: błąd kwantyzacji – jest czynnikiem, który degraduje sygnał analogowy poddany procesowi konwersji cyfrowej. Jest tym większy, im mniejsza rozdzielczość przetwornika cyfrowo-analogowego. Przyjrzyjmy się trochę bliżej temu zjawisku. Na rysunku 18 pokazano genezę błędu kwantyzacji.
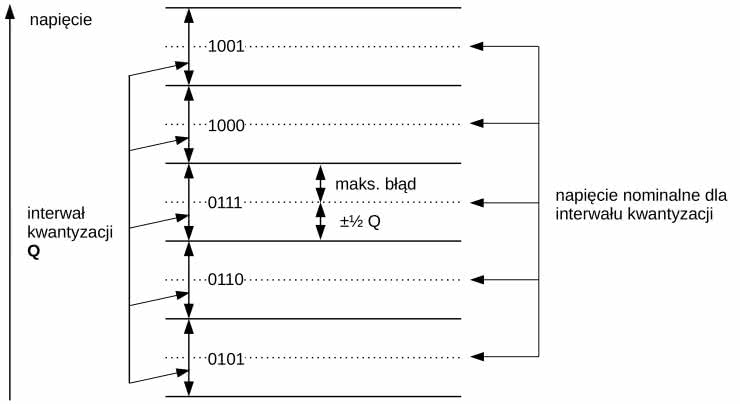
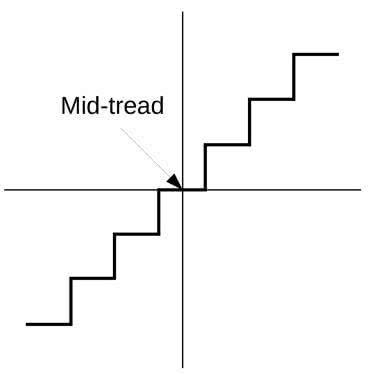
Kwantowanie przypisuje dyskretne liczby do zmiennych wartości napięcia. Wszystkim napięciom w tym samym przedziale kwantyzacji przypisuje się tę samą liczbę, co powoduje, że przetwornik DAC wytwarza potem napięcie plasujące się w środku przedziałów o długości Q (pokazanych liniami przerywanymi). Jest to charakterystyka kwantyzatora typu mid-tread.
Na rysunku 19 pokazano tzw. funkcję przejścia takiego idealnego kwantyzatora, czyli – innymi słowy – wykres zależności wyjścia układu od aktualnego stanu jego wejścia. W audio, gdy używamy terminu „liniowość”, mamy zazwyczaj na myśli prostoliniową funkcję przejścia. Liniowość jest w technice audio pożądanym celem, jednak – jak widać na rysunku 19 – idealny kwantyzator nie ma absolutnie charakterystyki liniowej i... to jest główny problem. Funkcja przejścia wygląda jak profil schodów. Przy napięciu analogowym równym zero woltów powinniśmy otrzymać tylko cyfrową wartość zero – a tak nie jest. Wyjściowa wartość kwantyzatora jest bowiem równa zeru dla wejściowych napięć różnych od zera, obejmujących cały przedział kwantyzacji Q. Bezwzględny zakres tych napięć jest określony przez rozdzielczość przetwornika i wartość napięcia referencyjnego. Omawiany układ to tak zwany kwantyzator środkowego stopnia, powszechnie używany w technice audio. Dokładnie taki sam problem występuje w konwersji cyfrowo-analogowej.
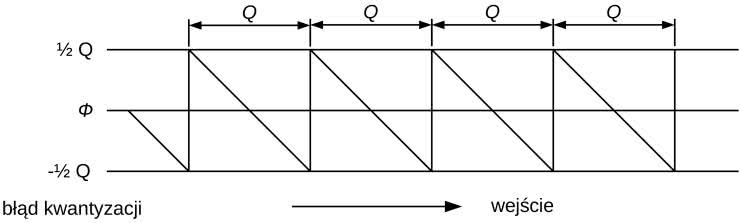
Jak widać, kwantowanie wprowadza pewien błąd napięcia w próbce audio, spowodowany przez różnicę między rzeczywistą funkcją przejścia (schodkową), a idealną linią prostą. Na rysunku 20 pokazano go jako funkcję piły, która ma okres równy Q. Amplituda nie może przekraczać ±½Q od szczytu do szczytu.
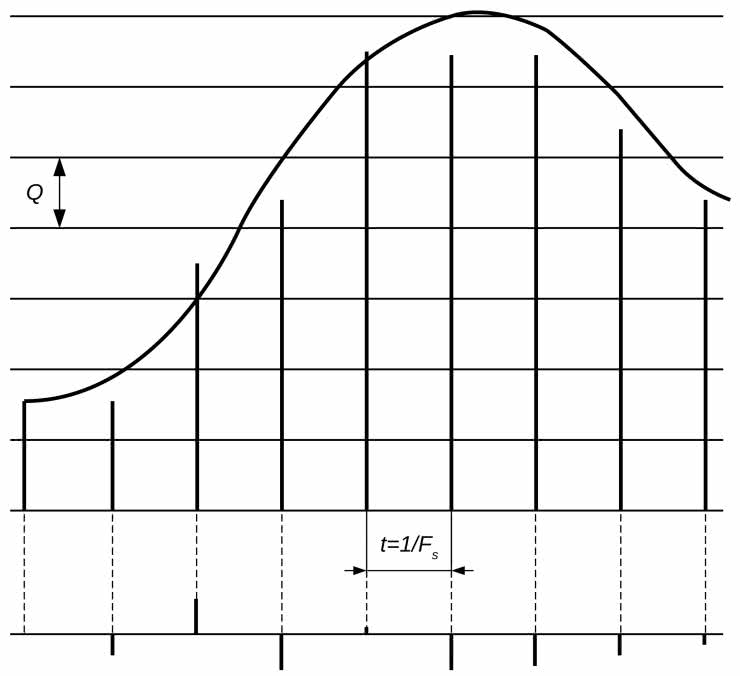
Błąd kwantyzacji można również badać w dziedzinie czasu. Dla uproszczenia pominiemy zmiany pasma wyjściowego, wywołane efektem apertury przetwornika cyfrowo-analogowego. Załóżmy więc, że próbki wyjściowe mają pomijalny czas trwania. Następnie impulsy z przetwornika cyfrowo-analogowego można porównać z teoretycznie wyliczonymi impulsami, wyznaczonymi dla oryginalnego sygnału analogowego. Różnica pomiędzy tymi impulsami będzie stanowiła impulsy reprezentujące błąd kwantyzacji – patrz rysunek 21.
Poziome linie na rysunku to granice między interwałami kwantyzacji, a krzywa to przykładowy, wejściowy sygnał analogowy. Pionowe paski to skwantowane próbki, które są pobierane w środku interwału kwantyzacji. Impulsy reprezentujące różnicę pomiędzy impulsami z wyjścia kwantyzatora a rzeczywistą wartością sygnału wejściowego pokazano na dole rysunku 21. Reprezentują one przebieg błędu kwantyzacji, postrzegany jako niepożądany sygnał, który w procesie kwantyzacji dodaje się do oryginalnego sygnału. Dodatkowo jeżeli bardzo mały sygnał wejściowy pozostaje całkowicie w jednym interwale kwantyzacji, to błąd kwantyzacji staje się sygnałem wyjściowym kwantyzatora. Ponieważ funkcja przenoszenia jest nieliniowa, idealna kwantyzacja powoduje zniekształcenia. W rezultacie rzeczywiste, cyfrowe urządzenia audio celowo używają nieidealnych kwantyzatorów, z mechanizmami pomagającymi linearyzować charakterystykę przejścia kwantyzacji.
Co poza tym możemy z tym zrobić? Ponieważ wielkość błędu kwantyzacji jest ograniczona, jego wpływ można zminimalizować zwiększając sygnał. Będzie to wymagało większej liczby interwałów kwantyzacji i większej liczby bitów do ich wyrażenia.
Gdy sygnał wejściowy obejmuje cały zakres kwantyzacji i ma złożony kształt (np. w muzyce orkiestrowej), kolejne próbki będą miały bardzo różne wartości liczbowe, a błąd kwantyzacji danej próbki będzie niezależny od błędu kwantyzacji innych próbek. W takim przypadku rozmiar błędu kwantyzacji będzie rozłożony z równym prawdopodobieństwem między swoimi granicami i niepożądany sygnał (dodany przez kwantyzację) staje się addytywnym, szerokopasmowym szumem, nieskorelowanym z sygnałem. Wtedy właściwe jest nazwanie go szumem kwantyzacji. To dobra wiadomość, bo w przypadku dużego sygnału szum jest maskowany przez właściwy przebieg użyteczny. W tych warunkach można obliczyć znaczący stosunek sygnału do szumu jako:
SNR=6,02+n·1,76 dB
gdzie n jest rozdzielczością bitową kwantyzacji.
Przykładowo system szesnastobitowy będzie oferował SNR na poziomie około 98,1 dB. Powyższy wynik jest prawdziwy dla dużej, złożonej fali wejściowej, ale metody zakładające, że błąd kwantyzacji jest zawsze szumem, dają wyniki, które niestety nie są zawsze prawdziwe. Przy niskich poziomach dźwięku błąd kwantyzacji przestaje być losowy i staje się funkcją przebiegu wejściowego, a ta – jak wiemy – nie jest liniowa. Gdy niepożądany sygnał (błąd kwantyzacji) staje się deterministyczną funkcją pożądanego sygnału, musi zostać sklasyfikowany jako zniekształcenie, a nie szum. Zniekształcenie można również przewidzieć na podstawie nieliniowości lub schodkowej natury funkcji przejścia.
Jak wiadomo, nieliniowość funkcji przejścia powoduje zniekształcenia, a te generują częstotliwości harmoniczne. Niestety, w procesie konwersji analogowo-cyfrowej zniekształcenia te są generowane po filtrze antyaliasingowym, więc każda składowa częstotliwościowa , która przekracza połowę częstotliwości próbkowania, będzie źródłem aliasingu. Powstają zatem zniekształcenia, które przypominają ćwierkanie ptaków – tzw. zniekształcenia intermodulacyjne (znane jako granulacja) oraz modulacja szumów.
Główną przyczyną tych wszystkich niekorzystnych zjawisk jest nieliniowa funkcja przejścia idealnego kwantyzatora. Nie trzeba dodawać, że każdy z powyższych efektów uniemożliwiłby użycie idealnego kwantyzatora do konwersji wysokiej jakości. Jedynym rozwiązaniem jest linearyzacja tej funkcji.
Dithering
Negatywne efekty nieliniowości idealnego kwantyzatora powinny (i mogą) być całkowicie wyeliminowane w praktycznym sprzęcie dzięki zastosowaniu ditheringu. Nie można przecenić znaczenia prawidłowego ditheringu kwantyzatora, ponieważ – jak już wiemy – nieliniowość nieodwracalnie zniekształca przekonwertowany sygnał i nie istnieje proces, który pozwoli to zniekształcenie usunąć.
Jak już powiedzieliśmy przy okazji opisu wysokich poziomów sygnału, błąd kwantyzacji jest w zasadzie szumem. W miarę spadku poziomu sygnału błąd kwantyzacji idealnego kwantyzatora silniej koreluje z sygnałem, a wynikiem są zniekształcenia nieliniowe (harmoniczne). Jeśli błąd kwantyzacji można by w jakiś sposób „odkorelować” od sygnału wejściowego, to system kwantowania może się stać liniowy. Mechanizm dithera wykonuje to zadanie sprawiając, że działanie kwantyzatora staje się nieprzewidywalne i nadaje systemowi poziom szumu taki, jak w systemie analogowym.
Jak działa dithering? Jedną z metod jest dodanie pseudolosowego szumu z równomiernym rozkładem prawdopodobieństwa i amplitudą szczytową równą przedziałowi kwantyzacji Q analogowego sygnału sprzed kwantowania. Ten sam sygnał zostaje później odjęty od sygnału analogowego powstałego po konwersji cyfrowo-analogowej. Ta metoda nazywa się ditheringiem subtraktywnym i ma tę zaletę, że amplituda ditheringu nie jest krytyczna – szum ma pełną niezależność statystyczną od sygnału i ten sam poziom, co błąd kwantyzacji w przypadku dużego sygnału bez ditheringu. Niestety, proces ten niesie ze sobą pewne wady praktyczne, ponieważ oryginalny przebieg szumu musi towarzyszyć próbkom lub być synchronicznie odtwarzany w przetworniku cyfrowo-analogowym. Jak się łatwo domyśleć, w systemach audio jest to bardzo trudne do wykonania, szczególnie w przypadku rozwiązań konsumenckich.
Dodatkowo działanie takie jest praktycznie niemożliwe w systemie, w którym dźwięk mógł zostać edytowany lub w którym jego poziom został zmieniony przez przetwarzanie, ponieważ szum musi pozostać synchroniczny i być przetwarzany w ten sam sposób. W praktyce wszystkie cyfrowe systemy audio korzystają z niesubtraktywnego dithera, w którym sygnał ditheru jest dodawany przed kwantyzacją i nie podejmuje się próby jego późniejszego usunięcia w DAC.
Jak już powiedzieliśmy, wprowadzenie dithera przed konwencjonalnym kwantyzatorem nieuchronnie prowadzi do niewielkiej redukcji stosunku sygnału do szumu, ale ta redukcja jest niewysoką ceną za eliminację nieliniowości. Szum w sygnale jest akceptowalny przez nasz zmysł słuchu, ponieważ jest nieodłącznym elementem towarzyszącym sygnałom analogowym – odwrotnie niż zniekształcenia harmoniczne, szczególnie w przypadku małych sygnałów. Poza tym umiemy skutecznie usuwać szum z sygnału przez nadpróbkowanie i kształtowanie szumu w przetwornikach DAC, a usuniecie zniekształceń harmonicznych nie jest już możliwe. Technika kształtowania szumu w konwersji DAC – w połączeniu z ditheringiem w konwersji ADC – pozwala uzyskać jakość przewyższającą osiągi systemów z ditheringiem subtraktywnym.
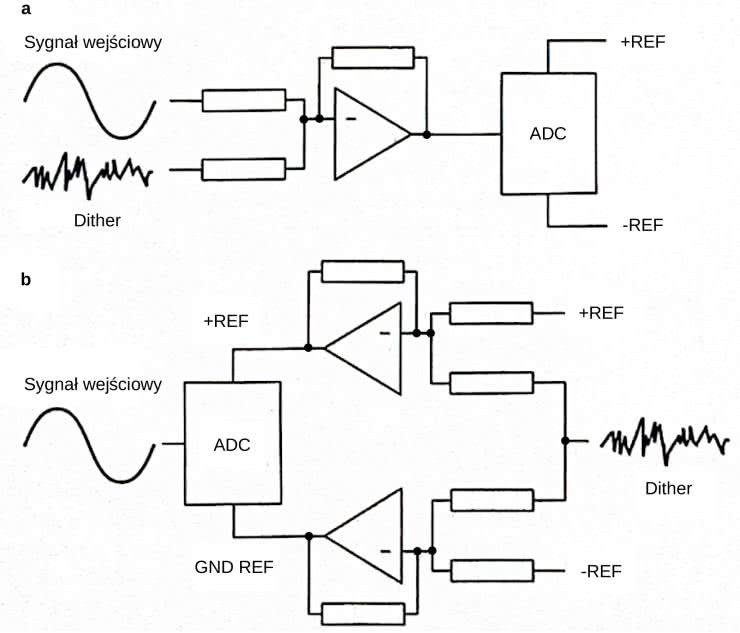
Idealny (bezszumowy) kwantyzator ma stałe przedziały kwantyzacji i zawsze musi generować ten sam błąd kwantyzacji przy tym samym sygnale. Na rysunku 22 pokazano sposób ditheringu idealnego kwantyzatora przez liniowe dodawanie kontrolowanego poziomu szumu – albo do analogowego sygnału wejściowego, albo do napięcia odniesienia, które jest używane do wyprowadzenia przedziałów kwantyzacji.
Dodanie ditheru oznacza, że kolejne próbki skutecznie przekraczają interwały kwantyzacji w różnych miejscach skali napięcia. Błąd kwantyzacji staje się funkcją ditheru, a nie przewidywalną funkcją sygnału wejściowego. Co ważne, błąd kwantyzacji nie jest eliminowany, ale subiektywnie przykre dla naszego słuchu, a więc – w praktyce – niedopuszczalne zniekształcenia harmoniczne, są przekształcane w szerokopasmowy szum. Ten zaś – jak już wiemy – jest akceptowany przez nasz zmysł słuchu i dodatkowo można go potem usuwać po stronie konwersji DAC.
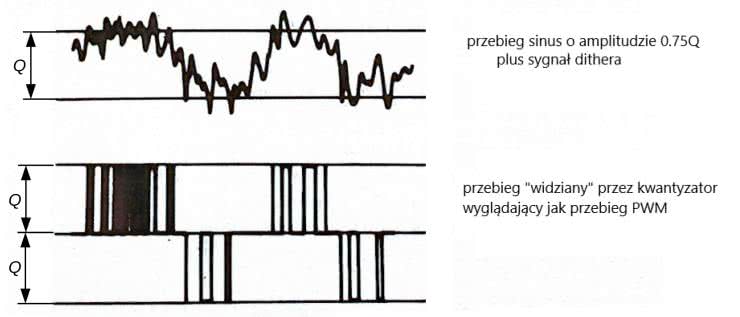
Rozważmy sytuację, w której analogowy sygnał wejściowy o niskiej amplitudzie zmienia się powoli w tym samym przedziale kwantyzacji. W takim przypadku na wyjściu kwantyzatora – bez zastosowania ditheru – ten sam wyjściowy kod numeryczny jest generowany w wielu okresach próbkowania, a następujące w tym czasie zmiany sygnału są tracone. Dither zmusza kwantyzator do przełączania się między dwoma lub większą liczbą stanów. Im wyższe napięcie sygnału wejściowego w danym przedziale, tym bardziej prawdopodobne staje się, że kod wyjściowy przyjmie następną (wyższą) wartość, zaś odwrotna sytuacja ma miejsce w miarę obniżania się napięcia wejściowego. Dither powoduje więc podwyższanie rozdzielczości systemu, dzięki czemu nie jest ona ograniczona tylko przez wielkość przedziałów kwantyzacji. Pokazane to zostało na rysunku 23.
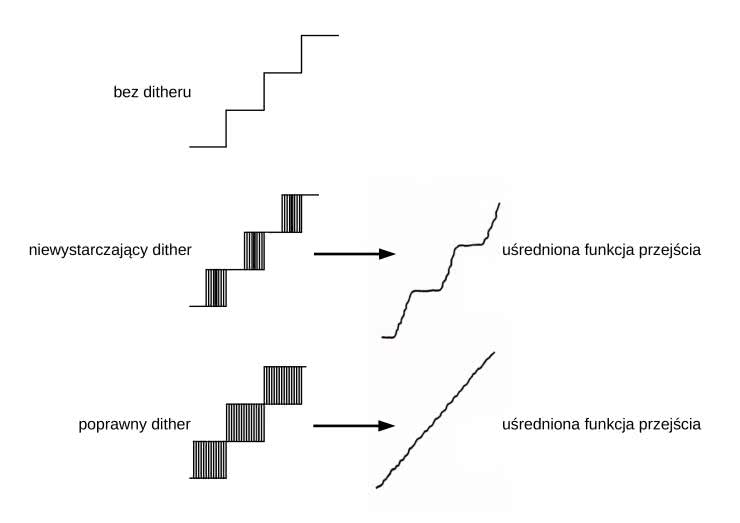
Działanie dithera można również analizować rozważając jego wpływ na funkcję przejścia kwantyzatora. Jak wiemy funkcja przejścia idealnego kwantyzatora jest schodkowa, ale w obecności dithera staje się ona „rozmyta w poziomie”, aż przy pewnej amplitudzie sygnału dithera średnia funkcja przejścia stanie się prosta – patrz rysunek 24.
Podsumowanie
W tym artykule zaprezentowaliśmy szereg teoretycznych zagadnień dotyczących konwersji cyfrowo-analogowej. Szczególnie istotne aspekty, które zostały omówione, to:
- odtwarzanie sygnału analogowego z impulsów na wyjściu konwertera cyfra-analog przez filtrowanie dolnoprzepustowe filtrem rekonstruującym,
- techniki nadpróbkowania i kształtowania szumów
- zasada działania interpolatora stosowanego do nadpróbkowania.
Dodatkowo zostało dogłębniej wyjaśnione zjawisko błędu kwantyzacji, jego wpływ na konwersję analogowo-cyfrową oraz działanie techniki ditheringu, pozwalającej redukować nieliniowości idealnego kwantyzatora. Dobrze dobrana technika ditheringu po stronie konwersji analogowo-cyfrowej, w połączeniu z kształtowaniem szumów po stronie konwersji cyfrowo-analogowej, daje solidne, teoretyczne i praktyczne podstawy do uzyskania bardzo dobrych parametrów szumowych oraz wyjątkowo niskich zniekształceń THD.
Tomasz Jabłoński, EP

 Zaloguj
Zaloguj