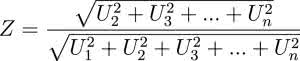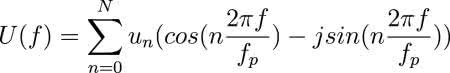Sposób pomiaru zawartości zniekształceń
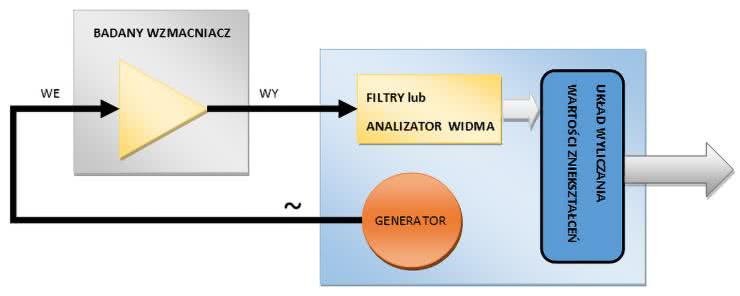
Pomiar zniekształceń polega w ogólności na podaniu na wejście badanego układu sygnału sinusoidalnego i pomiarze oraz analizie napięcia wyjściowego. Jedną z metod jest odfiltrowanie składowej o częstotliwości przebiegu wejściowego, a następnie porównanie tych wartości. Inna metoda polega na wyliczeniu transformaty Fouriera i wyznaczeniu zniekształceń na podstawie składowych harmonicznych widma. Schemat blokowy układu do pomiaru zniekształceń nieliniowych pokazano na rysunku 1.
Składowe harmoniczne są to sygnały o częstotliwości stanowiącej całkowitą wielokrotność częstotliwości napięcia wejściowego. Ich zawartość (Z) określa poziom zniekształceń, ponieważ każdy sygnał okresowy składa się tylko z sinusoidy o częstotliwości podstawowej oraz składowych harmonicznych:
gdzie napięcia Un – wartości kolejnych harmonicznych, U1 – wartość sygnału o częstotliwości podstawowej.
Algorytm programu
Algorytm pomiaru zniekształceń nieliniowych składa się z dwóch części: generatora sygnału sinusoidalnego oraz procedury obliczającej poziom zawartości składowych harmonicznych. Do pomiaru składowych wprowadzanych przez zniekształcenia harmoniczne zastosujemy metodę analizy częstotliwościowej, co oznacza, że obliczymy dyskretną transformatę Fouriera. Pozwala nam ona zidentyfikować wartość składowej sygnału o określonej częstotliwości. Ponieważ z obliczeń uzyskujemy wartość w postaci zespolonej, w celu wyznaczenia wartości rzeczywistej należy wyznaczyć moduł owej liczby zespolonej.
Transformata Fouriera sygnału dyskretnego ma postać:
gdzie:
- f – częstotliwość, dla której wyznaczamy wartość składowej,
- fp – częstotliwość próbkowania,
- un – wartość n-tej próbki.
Jeśli znamy wartość sygnału w postaci zespolonej, czyli składającej się z części rzeczywistej i urojonej, możemy wyznaczyć jej wartość rzeczywistą, która jest modułem danej wielkości.
gdzie:
- Uˆ – wartość zespolona,
- UR – wartość rzeczywista,
- Uℜ – składowa rzeczywista,
- Uℑ – składowa urojona.
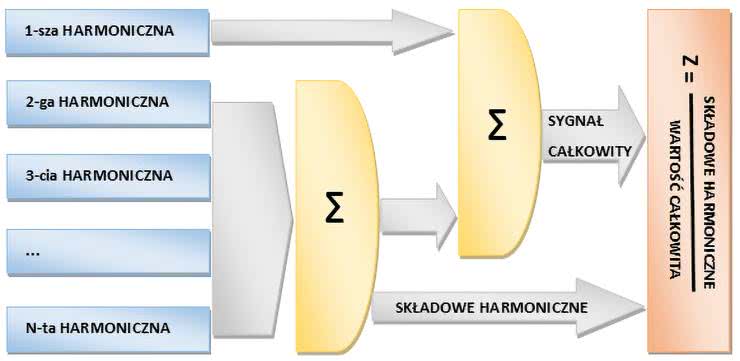
W naszym programie wyliczamy tylko wartości dla częstotliwości, których wielokrotnością jest częstotliwość próbkowania (czyli 48 kHz). Najlepiej przyjąć właśnie takie rozwiązanie, gdyż umożliwia ono uzyskanie najdokładniejszego wyniku. Częstotliwość próbkowania ogranicza nam też maksymalną mierzalną składową harmoniczną, która powinna być co najmniej dwa razy mniejsza od tejże częstotliwości. W naszym przypadku przyjąłem 12 kHz. Pomiar wyższych częstotliwości harmonicznych nie jest konieczny, gdyż zazwyczaj zniekształcenia nieliniowe wprowadzają najniższe harmoniczne. Ogólna idea wyznaczania zniekształceń została zobrazowana na rysunku 2.
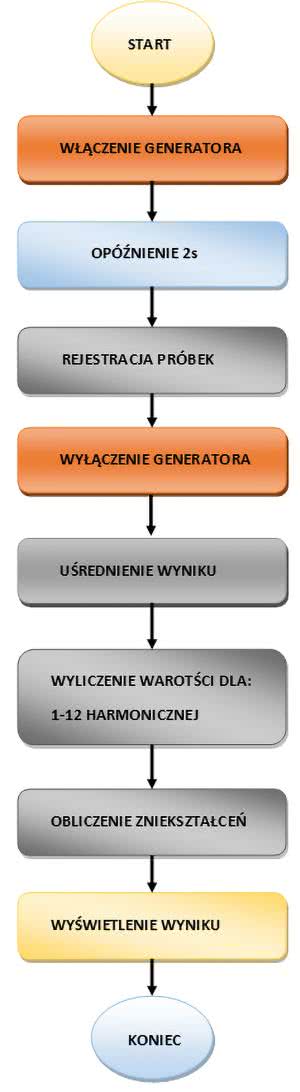
W celu zmniejszenia poziomu zakłóceń zarejestrowane dane zostają uśrednione. Pomiar wykonujemy dla 500 okresów, a następnie wyliczamy średnią arytmetyczną dla każdej próbki okresu. Wykaz kolejnych operacji wykonania pomiaru zniekształceń nieliniowych pokazano na rysunku 3.
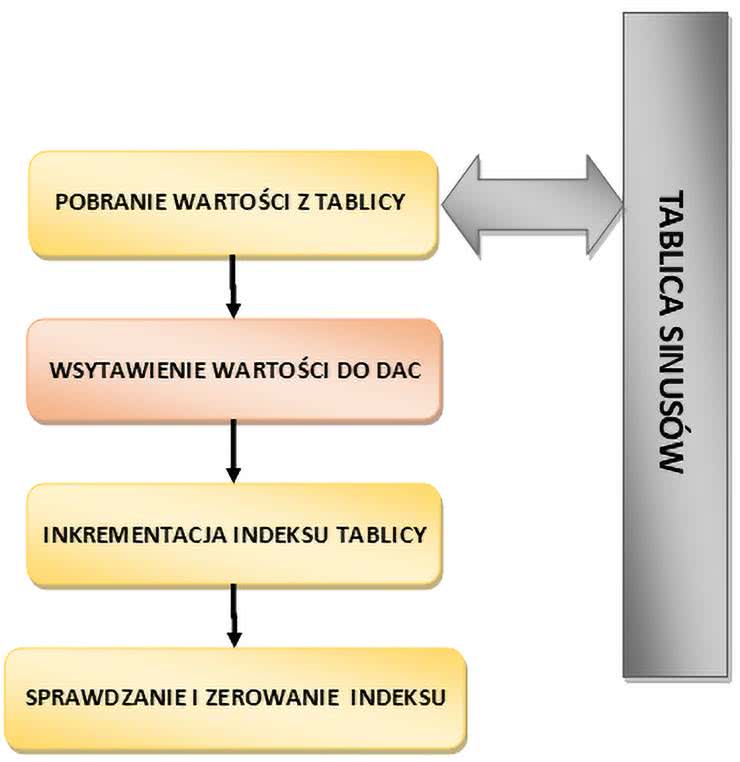
W generatorze sygnału sinusoidalnego stosujemy tablicę z zapamiętanymi wartościami tej funkcji, co znacznie przyspiesza działanie programu. Algorytm polega na odczytywaniu kolejnych wartości z tablicy i przesyłaniu ich do przetwornika cyfrowo analogowego w CODEC. Uproszczony algorytm działania generatora pokazany został na rysunku 4, natomiast kody procedur wyznaczania zniekształceń i generatora sygnału sinusoidalnego oraz rejestracji danych widoczne są na listingach 1 i 2.
{
H_1,
H_2,
H_3,
H_4,
H_6,
H_8,
H_9,
H_12,
};
float TabHarm[8];
float TabPr[N_OKR];
float ObliczTr(float f)
{
float OM = 2*STALA_PI*f/FP;
int i;
float tfi = 0, tfr =0;
for(i=0;i<N_OKR;++i)
{
tfr += TabPr[i]*cosf(OM*i);
}
for(i=0;i<N_OKR;++i)
{
tfi += -TabPr[i]*sinf(OM*i);
}
return sqrtf(tfr*tfr+tfi*tfi);
}
void ObliczH()
{
static float ftab[] = {1000, 2000,3000,4000,6000,8000,9000,12000};
int i;
for(i=H_1; i<=H_12;++i)
TabHarm[i] = ObliczTr(ftab[i]);
}
float ObliczWZ()
{
float uc = 0, uh = 0;
int i,j;
float s;
for(i=0;i<N_OKR;++i) // Obliczanie wartości średnich
{
s = 0;
for(j=0;j<N_POM;++j)
{
s+=BufPr.Pr[j][i];
}
TabPr[i] = s/(float)N_POM;
}
ObliczH(); //Obliczanie harmonicznych
// obliczanie współczynnika zniekształceń
for(i=H_1; i<=H_12;++i)
uc += TabHarm[i]*TabHarm[i];
for(i=H_2; i<=H_12;++i)
uh += TabHarm[i]*TabHarm[i];
return sqrtf(uh)/sqrtf(uc);
}
Listing 1. Fragment programu odpowiedzialny za obliczanie poziomu zniekształceń
{
float wy = 0;
if(StartPom)
{
LicznikOp = 0;
GenWl = true;
StartPom = false;
}
if(GenWl)
{
if(LicznikOp>=N_OP)
{
if(LicznikOp<N_POM*N_OKR+N_OP)
{
float w = ((float)WartoscWE_L + (float)WartoscWE_P)/(float)0x7FFF;
BufPr.Tab[LicznikOp-N_OP] = w;
} else
{
GenWl = false;
KoniecPom = true;
}
}
wy = WSP_GA*GAmp*TabSin[(LicznikOp)%N_OKR];
++LicznikOp;
}
wy = WSP_GA*GAmp*TabSin[(LicznikOp)%N_OKR];
++LicznikOp;
WartoscWY_P = WartoscWY_L = (int16_t)(wy*(float)0x7FFF);
}
Listing 2. Fragment programu odpowiedzialny za rejestrację danych
Interfejs użytkownika
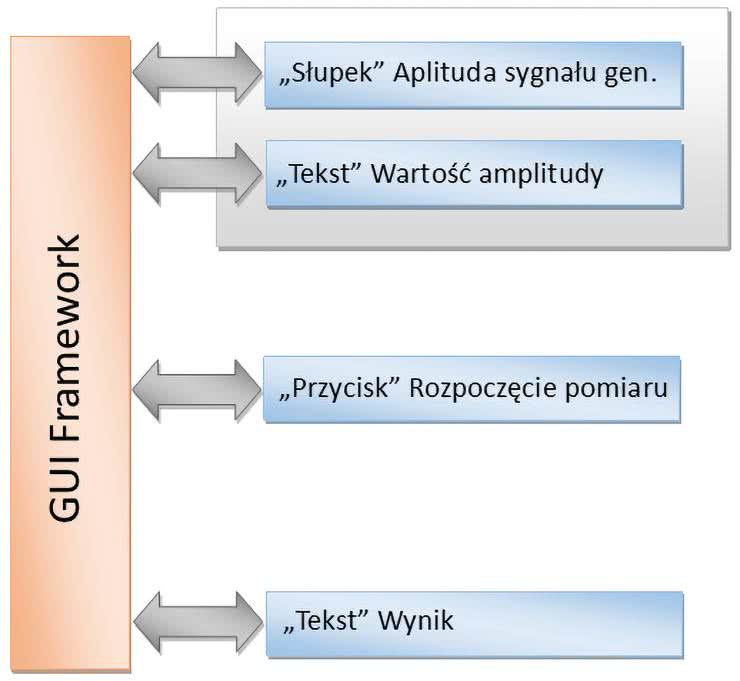
Do stworzenia interfejsu użytkownika użyto biblioteki napisanej przez autora. Współpracuje ona z wyświetlaczem graficznym 128×64 pikseli oraz obsługuje enkoder inkrementalny. W naszym przypadku zastosowaliśmy trzy obiekty interfejsu: słupek przyrostu, pole tekstowe oraz przycisk. Jedno z pól tekstowych – wraz ze słupkiem progresu – służy do wskazywania ustawionej za pomocą enkodera amplitudy sygnału. Kolejny obiekt, również typu pola tekstowego, służy do wyświetlania wyniku, czyli wartości zniekształceń nieliniowych. Wybranie pola typu przycisk powoduje rozpoczęcie pomiaru. Schemat obrazujący działanie interfejsu pokazany jest na rysunku 5.
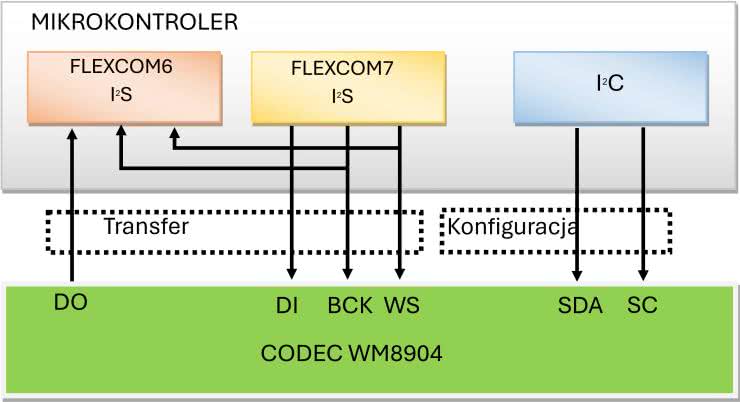
W skrócie opiszę jeszcze komunikowanie się procesora z CODEC. Konfiguracja procesora dźwiękowego odbywa się poprzez interfejs I²C, natomiast przesyłanie danych odbywa się w standardzie I²S. W mikrokontrolerze PLC55S28 każdy interfejs przesyłania danych realizuje się za pomocą odpowiednio skonfigurowanego uniwersalnego bloku WE.WY (FLEXCOM). Niestety, w tym rozwiązaniu nie można stworzyć pojedynczego interfejsu I²S zapisującego i odczytującego dane. Trzeba więc zastosować dwa bloki FLEXCOM (możliwości procesora umożliwiają połączenie dwóch takich bloków). W naszym przypadku do komunikacji w standardzie I²C stosujemy bloki FLEXCOM 6 i 7. Natomiast procedura przetwarzania dźwięku zapisana jest w procedurze obsługi przerwania kontrolera tych interfejsów. Schemat blokowy odzwierciedlający komunikację kodeka z mikrokontrolerem pokazany jest na rysunku 6.
Obsługa programu
Działanie programu okazuje się bardzo proste. Po podłączeniu wejścia i wyjścia akustycznego badanego układu wystarczy ustawić amplitudę sygnału wyjściowego generatora, a następnie wcisnąć przycisk na płytce modułu. Po przeprowadzeniu badania na wyświetlaczu pojawi się wartość zniekształceń.
Pomiar trwa około 2 s. Czas ten jest tak długi ponieważ na jego wartość składa się wartość specjalnie wprowadzonego opóźnienia i dopiero następującego po nim odczytu sygnału wyjściowego. Wprowadzenie tego opóźnienia wynika z faktu, że w niektórych wzmacniaczach (z powodu nieliniowej charakterystyki) dochodzi do przesunięcia punktu pracy. Dlatego, po włączeniu sygnału z generatora, program wprowadza opóźnienie, które umożliwia dokładne ustalenie się warunków pracy badanego wzmacniacza.
Układ elektroniczny
Do użytego modułu dodano dwie modyfikacje: układ bufora do sterowania wyświetlaczem – ponieważ jest on zasilany napięciem 5 V, natomiast procesor pracuje na szynie 3,3 V – oraz dzielnik wejściowy podłączony do układu przez złącze mini Jack. Dzielnik jest potrzebny do pomiaru zniekształceń do wzmacniaczy dużej mocy. Najlepiej stosować dzielniki przez 10 lub przez 100, np. rezystory 27 kΩ i 3 kΩ (1:10) lub 100 kΩ i 1 kΩ (1:100). Wartości dzielnika należy dobierać tak, aby nie przekroczyć wartości wejściowej sygnału 0,5 V. Przy badaniu wzmacniaczy niskosygnałowych można go pominąć.
Do pomiaru wzmacniaczy dużej mocy można użyć rezystorów obciążających wyjście o wartościach 4 Ω lub 8 Ω – wartość mocy wyjściowej wzmacniacza nie powinna przekraczać mocy znamionowej tych rezystorów. Mogą to być rezystory drutowe w obudowie ceramicznej (pojedyncze lub kilka, odpowiednio połączonych) albo rezystory z radiatorem.
Przykładowe zdjęcia tego typu elementów pokazano na fotografiach 1a, 1b i 2.
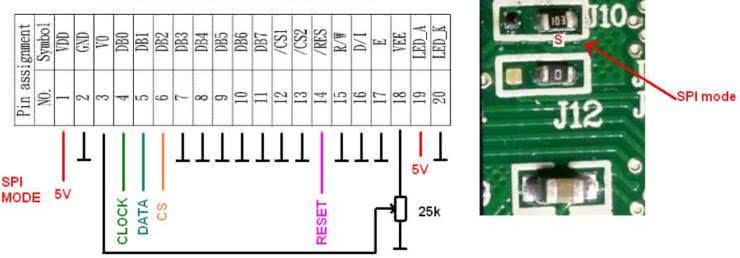
Podłączenie dzielnika do płytki zaprezentowano na fotografii 3, a rysunki 7 i 8 pokazują podłączenie wyświetlacza do modułu.
Tomasz Krogulski

 Zaloguj
Zaloguj