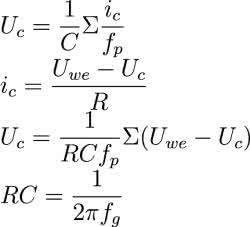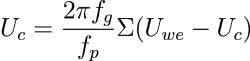Fuzz klasyczny dorównuje popularnością swojemu poprzednikowi, ale jego brzmienie jest ostrzejsze. Duży wpływ na brzmienie tego efektu ma pasmo sygnału wejściowego dlatego dla jego modyfikacji zastosowano regulowany filtr górnoprzepustowy II rzędu. W zaprezentowanym rozwiązaniu i w torze dźwiękowym, bezpośrednio przed samym fuzzem zastosowano filtr górnoprzepustowy drugiego stopnia. Natomiast po przetworzeniu sygnału przez algorytm efektu następuje filtracja niskich częstotliwości. Zastosowanie filtru dolnoprzepustowego ma na celu złagodzenie brzmienia lub jego przytłumienie.
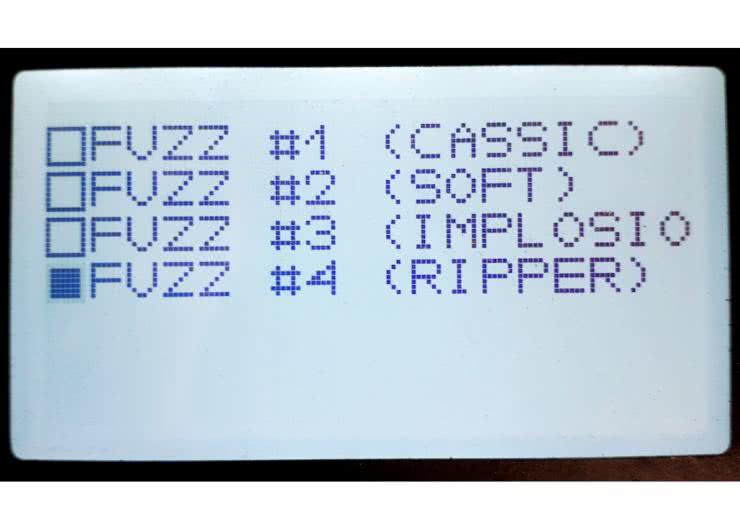
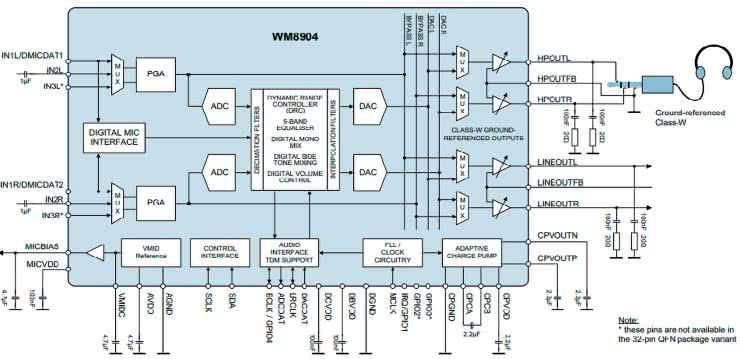
Ponadto w projekcie dostępne są 4 rodzaje efektu fuzz, które wprowadzają zarówno zniekształcenia o naturalnym brzmieniu, jak i dość nietypowe efekty akustyczne. Do zamiany sygnału analogowego na cyfrowy oraz konwersji w przeciwną stronę - podobnie jak w poprzednich rozwiązaniach - stosowany jest 16-bitowy kodek, znajdujący się na płytce modułu. Do sterowania parametrami urządzenia służą przyciski umieszczone na płytce oraz graficzny wyświetlacz monochromatyczny o rozdzielczości 128×64 px.
Koncepcja urządzenia
Działanie urządzenia jest dość proste. Sygnał akustyczny, zmieniony na postać cyfrową, jest filtrowany przez FGP o regulowanej częstotliwości granicznej, a następnie wprowadzane są zniekształcenia. Do wyboru mamy cztery rodzaje zniekształceń:
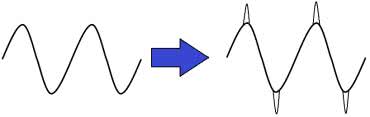
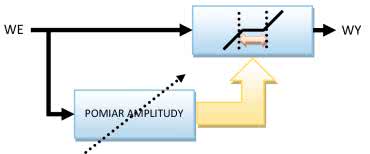
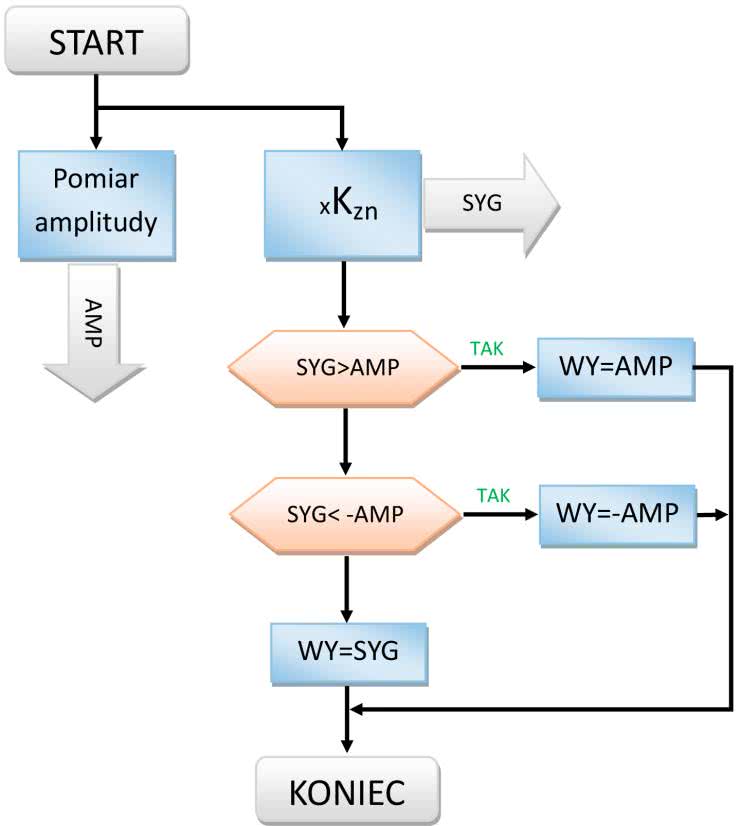
• Fuzz klasyczny - polega na silnym wzmocnieniu sygnału, a następnie ograniczeniu jego wartości (rysunek 1).
• Fuzz o stałych zniekształceniach - w tym przypadku sygnał ulega nieznacznemu wzmocnieniu, a amplituda jest ograniczana na poziomie jego wartości wejściowej (zasada wprowadzania zniekształceń jest taka sama, jak w poprzednim rozwiązaniu). Wizualizację opisanej metody również pokazuje rysunek 1.
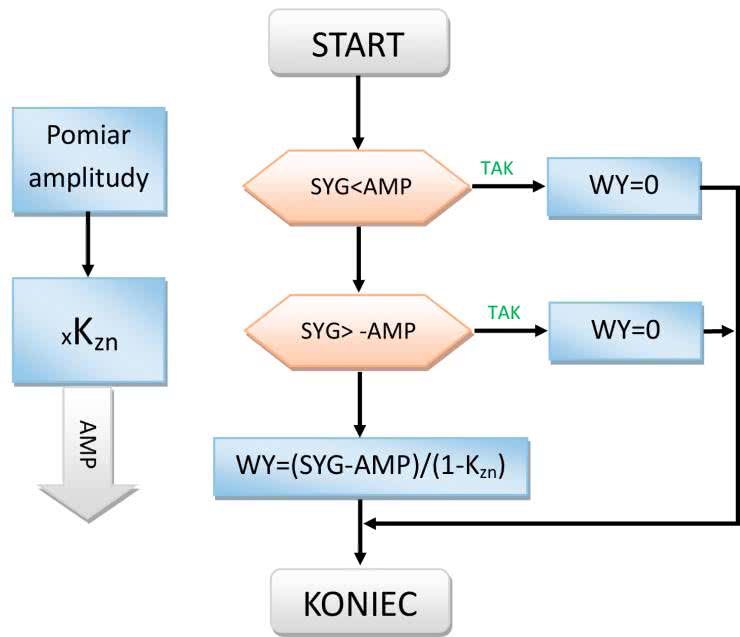
• Efekt polegający na tym, że z sygnału odcinana jest dolna część (pomiędzy zerem a ustalonym poziomem) - patrz rysunek 2.
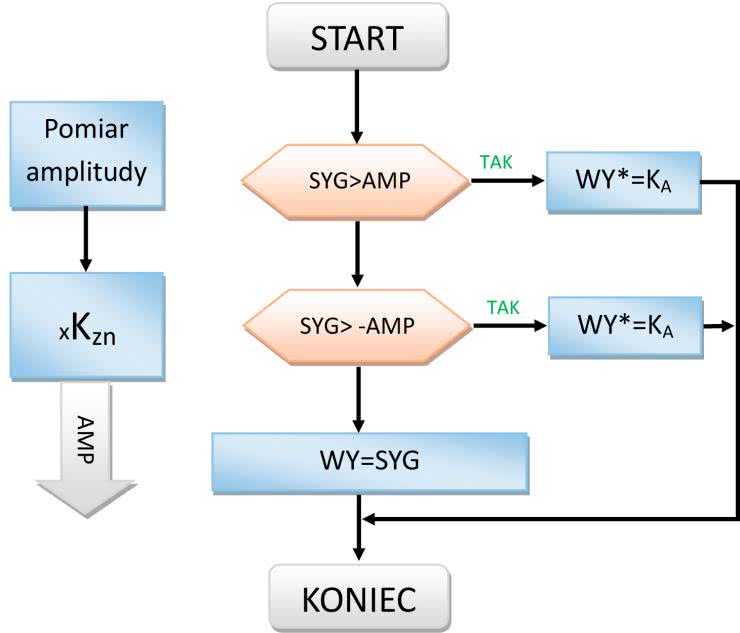
• Efekt polegający na zwiększaniu wzmocnienia powyżej określonej wartości amplitudy sygnału; wywołuje wrażenie dźwiękowe podobne do pękania (rysunek 3).
Zasada działania układów wprowadzających zniekształcenia
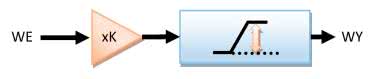
Działanie pierwszego typu efektu distrotion opiera się na dużym wzmocnieniu sygnału akustycznego, które jest regulowane, a następnie na ograniczeniu jego wartości. Proces ten ilustruje rysunek 5.
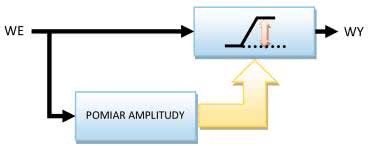
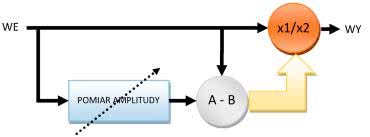
W drugim rodzaju efektu wprowadzane zniekształcenia mają tę samą wartość, niezależną od amplitudy. W układzie tym wykonujemy pomiar wartości sygnału, a następnie ograniczamy ją, w zależności od zmierzonej amplitudy. Obrazuje to rysunek 6.
Trzeci typ układu wprowadzający zniekształcenia odcina od sygnału jego dolną wartość. Tu też mierzymy wartość sygnału, a układ ograniczający jest od niej zależny (rysunek 7).
W ostatnim z opisywanych rodzajów układu zniekształcającego poziom sygnału jest mierzony i porównywany z jego wartością chwilową. Jeśli amplituda przekroczy pewną wartość (proporcjonalną do zmierzonego poziomu), zmianie ulega wartość wzmocnienia (rysunek 8).
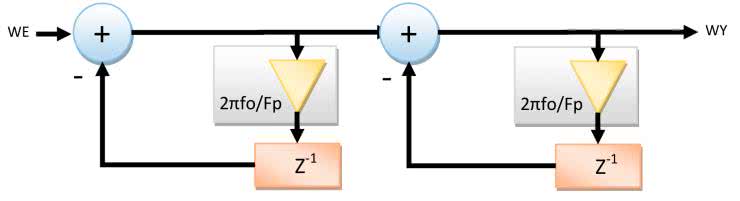
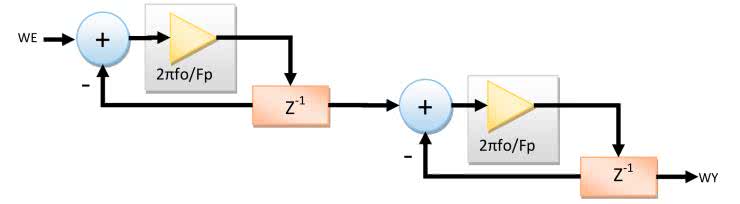
Jak już wspomniałem we wstępie do niniejszego artykułu, układ zniekształcający poprzedza filtr górnoprzepustowy. Struktura tego filtru pokazana jest na rysunku 9.
Bloki Z-1 symbolizują rejestry pamiętające. Układ działa poprzez analogię do zwykłego układu RC. W algorytmie wykorzystujemy zasadę, że napięcie (Uc) na kondensatorze o pojemności (C) jest całką płynącego przezeń prądu (ic). Natomiast wartość tego prądu zależy - jak wiemy z prawa Ohma - od spadku napięcia na rezystorze oraz jego wartości (R). Wartość napięcia na rezystorze stanowi różnicę napięcia wejściowego (Uwe) i wartości napięcia na kondensatorze (Uc).
gdzie:
- fg - częstotliwość graniczna filtru,
- fc - częstotliwość próbkowania.
czyli:
A z budowy układu różniczkującego wynika:
Schemat blokowy filtru dolnoprzepustowego można natomiast zobaczyć na rysunku 10.
Opis programu komputerowego
Cały program składa się z dwóch części: zestawu procedur przetwarzania sygnału (w których skład wchodzi również komunikacja z kodekiem) oraz obsługi interfejsu użytkownika (odpowiedzialnej za ustawianie parametrów urządzenia, obsługę przycisków sprzętowych i enkodera oraz sterowanie wyświetlaczem graficznym). Interfejs graficzny pomyślany został w taki sposób, że na wyświetlaczu prezentowane są obiekty służące do wprowadzania danych do programu. Ich stan lub wartość można zmieniać za pomocą enkodera, natomiast przełączać je można za pomocą dwóch przycisków. W naszym urządzeniu na wyświetlaczu znajduje się lista wyboru efektu oraz słupek do regulacji poziomu zniekształceń.
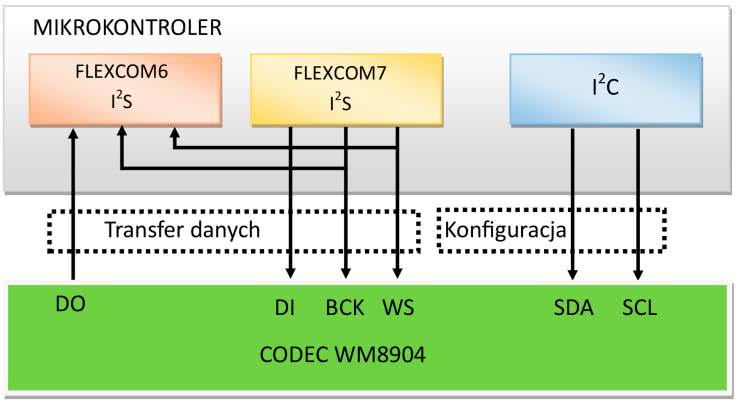
Część DSP. Sterowanie kodekiem
Ponieważ w poprzednich artykułach omówiłem szczegółowo transmisję pomiędzy mikrokontrolerem a kodekiem, w tym artykule zamieszczę jedynie ilustracje obrazujące jej działanie (rysunki 11 i 12).
Procedury DSP
Ponieważ ogólny zarys działania programu został opisany w poprzednich punktach, tym razem wyjaśnię tylko algorytmy procedur wprowadzających zniekształcenia oraz zamieszczę fragment programu źródłowego zawierający procedury DSP (listing 1). Główną procedurą w zaprezentowanym fragmencie kodu jest funkcja „PrzetwarzanieGłowne”, wywoływana w każdym cyklu próbkowania sygnału i odpowiednio rozdzielająca zadania przetwarzania sygnału pomiędzy różne warianty algorytmu i jego elementów.
static float n##c1, n##c2;\
n##c1 += (x-n##c1)*(float)k;\
x -= (n##c1+n##c2);\
n##c2 += x*(float)k;}
#define FDPII(n,k,x){\
static float n##c1, n##c2;\
n##c1 += (x-n##c1)*(float)k;\
n##c2 += (n##c1-n##c2)*(float)k;\
x=n##c2;}
float ZN = 0.5;
float FDP_K = 2*STALA_PI*5000/FP;
float FGP_K = 2*STALA_PI*200/FP;
int ENum = 0;
float __attribute__((section(".ramfunc.$SRAMX"))) F3(float we)
{
register float ww, wsp, ha, fk = 0.4+ZN;
PomiarAmplitudy(P_,we);
wsp = P_BA*fk;
ww = ((we>wsp) ? (we-wsp)/(1.41-fk):
((we<-wsp) ? (we+wsp)/(1.41-fk) : 0));
return ww;
}
float __attribute__((section(".ramfunc.$SRAMX"))) F4(float we)
{
register float pb;
register float ww = 0, fk = ((float)1.4-(float)1)*ZN+(float)1;
PomiarAmplitudy(P_,we);
pb = (we<0) ? -we : we;
ww = (pb>fk*P_BA) ? we*3 : we;
return ww/1.5;
}
float __attribute__((section(".ramfunc.$SRAMX"))) F1(float w)
{
register float ww = w;
ww *=(float)50*ZN;
ww = (ww>FUZZ_A) ? FUZZ_A : ((ww<-FUZZ_A) ? -FUZZ_A : ww);
return ww;
}
float __attribute__((section(".ramfunc.$SRAMX"))) F2(float w)
{
PomiarAmplitudy(PA_,w);
register float ba = PA_BA;
w *= ((float)50*ZN);
if(w>ba) return ba;
else if(w<-ba) return -ba;
else return 0;
}
void __attribute__((section(".ramfunc.$SRAMX"))) PrzetwarzanieGlowne()
{
static float (*FT[4])(float) = {F1,F2,F3,F4};
float w = ((float)WartoscWE_L + (float)WartoscWE_P)/(float)0x7FFF;
FGPII (fgp,FGP_K, w);
w = FT[ENum](w);
FDPII (fdp,FDP_K, w);
WartoscWY_P = WartoscWY_L = (int16_t)(w*(float)0x7FFF);
}
Listing 1. Fragment kodu prezentujący procedurę przetwarzania sygnału
Na rysunku 13 widać, że działanie tego algorytmu polega na porównywaniu wzmocnionego sygnału akustycznego z jego amplitudą - i w przypadku przekroczenia progu sygnał zostaje ograniczony do jej wartości.
Działanie algorytmu efektu typu 1 jest podobne, z tym że wartość sygnału akustycznego porównywana jest ze stałą wartością.
Efekt typu 3 (rysunek 14) również porównuje wartość sygnału akustycznego z poziomem zależnym od amplitudy sygnału, przy czym porównywana amplituda pomnożona zostaje przez współczynnik mniejszy od jedności. Sygnał wejściowy poniżej tej wyliczonej wartości ulega wyzerowaniu, natomiast wartość przekraczająca ją zostaje zmniejszona o tę właśnie wartość (porównywaną) oraz pomnożona przez wyliczony współczynnik (w celu kompensacji jej wielkości). Jest to konieczne, ponieważ odjęcie wartości progowej powoduje znaczne zmniejszenie poziomu sygnału.
Efekt typu 4 (rysunek 15) porównuje amplitudę sygnału z poziomem o wartości nieco mniejszej od wartości maksymalnej amplitudy. Jeśli sygnał przekracza tę wartość, jest mnożony przez stały współczynnik.
Opis układu elektrycznego
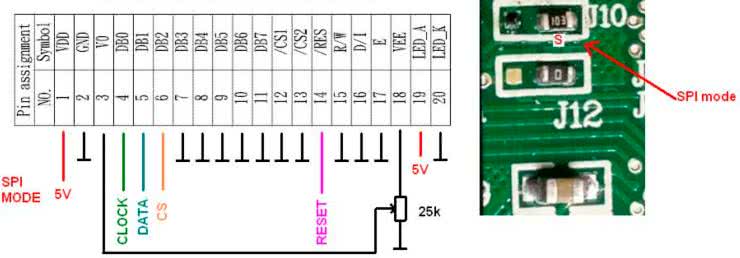
Chociaż układ zbudowany jest w oparciu o gotowy moduł z mikrokontrolerem firmy NXP, do jego działania potrzebnych będzie kilka elementów dodatkowych. Są to: wyświetlacz graficzny 128×64 piksele oraz układ do jego sterowania. Istnieje opcja dołączenia do modułu dwóch przycisków, choć nie ma takiej konieczności, bo do sterowania urządzeniem można wykorzystywać przyciski znajdujące się na płytce ewaluacyjnej. Zastosowany w naszym układzie wyświetlacz graficzny jest w stanie pracować w dwóch trybach. Może być sterowany za pomocą transmisji równoległej lub szeregowej w protokole SPI. W prezentowanym projekcie stosujemy tryb transmisji szeregowej. Ponieważ wyświetlacz fabrycznie skonfigurowany został do pracy przy transmisji równoległej, należy przełączyć zworę, która znajduje się na jego tylnej części (rysunek 16).
Dodatkowo - ponieważ układ logiczny wyświetlacza jest sterowany napięciami niezgodnymi ze standardem 3,3 V, czyli sygnałami wyjściowymi mikrokontrolera (wysoki stan wejść wymaga napięcia wyższego niż 3,5 V) - zastosowano bufor 74HCT541. Schemat części elektrycznej pokazany został na rysunku 17.
Elementy zastosowane w układzie
Aby uzyskać dobre wrażenie optyczne, w urządzeniu zastosowano monochromatyczny wyświetlacz graficzny LCD o rozdzielczości 128×64 px typu LCD-EG-128064H-FHW K/W-E6. Charakteryzuje się on niską ceną i jest dostępny w wielu sklepach internetowych, w tym także u polskich dystrybutorów. Jako bufor wykorzystano układ 74HCT541 - również łatwo dostępny i przystępny cenowo. Potencjometr do regulacji kontrastu może być dowolnym potencjometrem montażowym o rezystancji około 25 kΩ. Jako enkoder można zastosować dowolny trójwyjściowy enkoder inkrementalny.
Tomasz Krogulski

 Zaloguj
Zaloguj