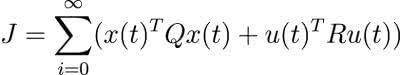Ball & Beam (3)

Wtorek, 01 Sierpień 2023

W ostatniej części artykułu zajmiemy się projektowaniem filtru Kalmana oraz regulatora LQR. Zagadnienia opisane w całym cyklu nie są łatwe, ale zaliczają się do fundamentalnych zagadnień w teorii sterowania, dlatego warto je przyswoić i przetestować z użyciem opisanej konstrukcji z belką i piłeczką. Zachęcam do własnych eksperymentów oraz testowania innych algorytmów sterowania.

Filtr Kalmana

Filtr Kalmana–Bucy jest obserwatorem stanu. Przy założeniu, że zakłócenia działające na obiekt są gaussowskie, zapewnia on optymalną estymatę. Teoretyczny opis filtru można znaleźć w [10]. My zaprojektujemy filtr, używając biblioteki PyControl [11]. Wszystkie obliczenia znajdują się w jupiter/LQG for 3D printed model.ipynb [12].

Jednak w pierwszej kolejności zdyskretyzujemy model, czyli przejdziemy z modelu z czasem ciągłym opisanym równaniem różniczkowym na model z czasem dyskretnym opisanym równaniem różnicowym. Skorzystamy z metody Eulera, która polega na zastąpieniu pochodnej ilorazem różnicowym:

gdzie T jest okresem próbkowania, który u nas wynosi 50 ms.

Aby wykonać obliczenia, najpierw musimy utworzyć obiekt sys. Definiujemy go poprzez cztery macierze – listing 1.

Listing 1. Obiekt sys zdefiniowany poprzez cztery macierze

A = [[0, 1, 0], [0, 0, 9.74], [0, 0, -1/0.051]]
B = [[0], [0], [1/0.051]]
C = [[1, 0, 0]]
D = [[0]]
Ts = 0.05

sys = control.ss(A, B, C, D)

Odpowiadają one naszym równaniom różniczkowym:

I zawierają zidentyfikowane wcześniej parametry. Dyskretyzację wykonujemy za pomocą funkcji:

dsys = control.sample_system(sys, Ts, method=’euler’)

Zwraca ona nowy obiekt dsys, zawierający zdyskretyzowany model.

Zakładamy, że na dyskretny model działają szumy gaussowskie w i v:

Ich macierze kowariancji są równe:

Filtr Kalmana jest systemem dynamicznym opisanym równaniem:

Pierwsze dwa składniki to po prostu symulacja zidentyfikowanego modelu. Trzecim składnikiem, a zarazem najważniejszym, jest macierz L, która wprowadza korektę na podstawie różnicy między zmierzonym wyjściem z modelu a wyjściem z symulowanego układu. Wartości jej współczynników możemy uzyskać za pomocą polecenia:

L, P, E = control.dlqe(dsys.A, [[0],[0],[1]], dsys.C, 1, 5)

Zacznijmy od opisu parametrów wejściowych funkcji control.dlqe. Pierwszy parametr to macierz A układu, drugi to macierz G opisująca, jak szum oddziałuje na stan. Założyłem, że jest on dodawany razem ze sterowaniem, więc macierz G i C mają tę samą postać. Trzeci parametr to macierz C. Ostatnie dwa parametry to wariancje szumów w i v. Zmieniając je, otrzymamy różne reakcje filtru. Wariancję pomiarową oszacowaliśmy przy kalibracji czujnika na około 5. Natomiast wariancję sterowania dobierzemy eksperymentalnie.

Wyjścia z funkcji control.dlqe są trzy: L jest macierzą współczynników filtru, wartość E to wektor wartości własnych macierzy przejścia w filtrze Kalmana. Wartość P jest rozwiązaniem równania Riccatiego dla naszego regulatora. Nam w tym momencie jest zbędna. Więcej na ten temat można znaleźć w [10].
Obiekt opisany równaniem różnicowym jest stabilny, gdy wszystkie wartości własne leżą wewnątrz koła o module jeden. Obliczamy moduły za pomocą polecenia:

print(np.abs(E))

Uzyskujemy wartości:

[0.92815779 0.92815779 0.01960784]

Jak widzimy, wszystkie one są mniejsze od 1, co oznacza, że wartości własne leżą wewnątrz okręgu o promieniu jeden, czyli układ jest stabilny.

Na potrzeby implementacji możemy przepisać filtr Kalmana do postaci:

Przetestujemy działanie filtru na danych używanych wcześniej do identyfikacji – listing 2.

Listing 2. Testowanie działania filtru na danych używanych wcześniej do identyfikacji

M = dsys.A-L*dsys.C
xe = np.zeros((N, 3))
xe[0] = [x[0], 0, 0]
for i in range(N-1):
xe[i+1] = np.dot(M, xe[i].transpose()) + \
np.dot(L, x[i]).transpose() + \
np.dot(dsys.B, u[i]).transpose()

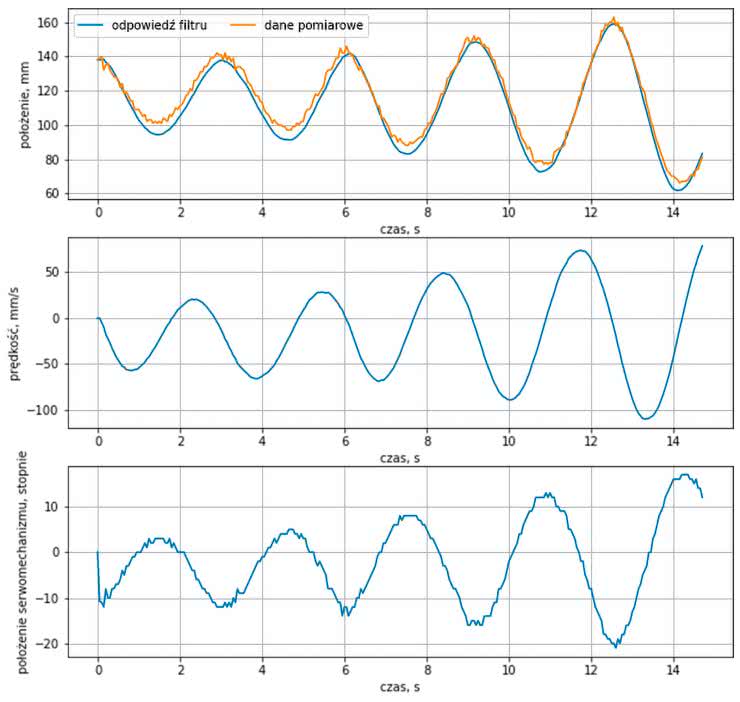
Wynik działania obserwatora widzimy na rysunku 21. Pierwszy wykres pokazuje porównanie pomiędzy odfiltrowanym położeniem a pomiarem. Pozostałe dwa wykresy to prędkość kulki i położenie serwomechanizmu.

Rysunek 21. Siły działające na kulkę

Do tej pory obliczenia prowadziliśmy z zastosowaniem liczb zmiennoprzecinkowych. Pozwalają one na reprezentację dużej dynamiki wartości: od bardzo małych do bardzo dużych. Kosztem jest jednak dłuższy czas prowadzenia obliczeń. Na Arduino chcemy zamiast nich zastosować liczby stałoprzecinkowe. Jednak współczynniki w filtrze mają bardzo duży zakres wartości od 1 do 10–8. Sprawdzimy więc, co się stanie, gdy będziemy symulować filtr, korzystając z liczb stałoprzecinkowych i pomijając zbyt małe współczynniki – listing 3. Dla współczynników przyjmujemy, że będą miały 3 miejsca po przecinku.

Listing 3. Symulacja filtru z zastosowaniem liczb stałoprzecinkowych i przy pominięciu zbyt małych współczynników

xe = xe_d[i]
xe_n = [0,0,0]

tmp = 804*xe[0] + 50*xe[1] + 196*x[i];
tmp_t[i][0] = tmp
xe_n[0] = tmp//1000;

tmp = -349*xe[0] + 1000*xe[1] + 487*xe[2] + 349*x[i];
tmp_t[i][1] = tmp
xe_n[1] = tmp//1000;

tmp = 20*xe[2] + 980*u[i];
tmp_t[i][2] = tmp
xe_n[2] = tmp//1000;

xe_d[i+1] = xe_n

Najpierw mnożymy współczynniki razy 1000, wynik zapisujemy w zmiennej tmp, a na końcu dzielimy je przez 1000. Uzyskalibyśmy podobny efekt, mnożąc i dzieląc przez potęgi dwójki. Wtedy mnożenia i dzielenia zastąpilibyśmy przez przesunięcia bitowe. Kosztem byłaby wtedy mniejsza czytelność.

W notatniku zostały wyrysowane wykresy uzyskanych wartości oraz wartości pośrednich obliczeń ze zmiennych tmp. Możemy porównać uzyskany wynik z wersją zmiennoprzecinkową oraz sprawdzić, czy wartości zmiennych pośrednich mieszczą się w zakresie, jaki może reprezentować zmienna typu long w Arduino: od –231 do 231–1.

Teraz możemy przejść do szkicu controler.ino i uzupełnić współczynniki w funkcji kalman – listing 4.

Listing 4. Szkic controler.ino z uzupełnionymi współczynnikami w funkcji kalman

void kalman(int xe_n[], int xe[], int x, int u) {
long tmp;
tmp = 804L*xe[0] + 50L*xe[1] + 196L*x;
xe_n[0] = tmp/1000;
tmp = -349L*xe[0] + 1000L*xe[1] + 487L*xe[2] + 349L*x;
xe_n[1] = tmp/1000;
tmp = 20L*xe[2] + 980L*u;
xe_n[2] = tmp/1000;
}

Regulator LQR

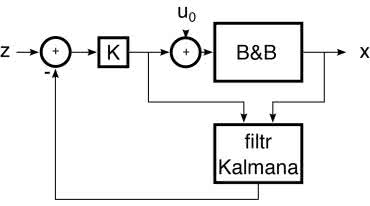
Po uzupełnieniu współczynników filtru możemy już eksperymentować z regulatorem ze sprzężeniem zwrotnym od stanu. Jego schemat pokazuje rysunek 22. Aby go uruchomić w GUI, wybieramy opcję Regulator type: from state. Następnie możemy eksperymentować, zmieniając wartości poszczególnych współczynników.

Rysunek 22. Schemat mechanizmu sterującego belką

Istnieją także inne metody doboru nastaw. Jedną z bardziej popularnych jest LQR – linear quadratic regulator. Jest to regulator z liniowym sprzężeniem zwrotnym minimalizujący kwadratową funkcję kosztów. Jest ona dana wzorem:

My skorzystamy z funkcji bibliotecznej, która przyjmuje obiekt dsys oraz współczynnik Q i R:

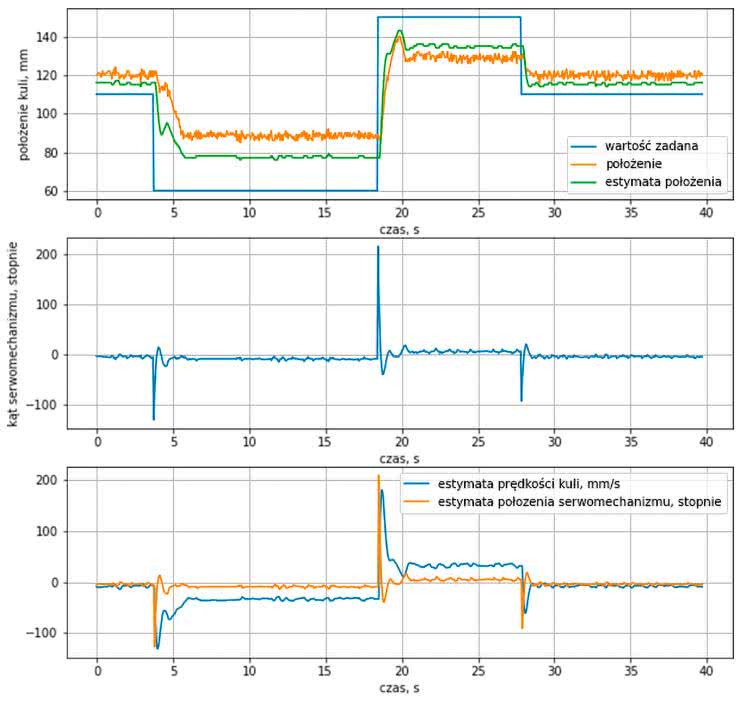
K, S, E = control.dlqr(dsys, [[100, 0, 0], [0, 1, 0], [0,0,1]], 1)

Kolejne współczynniki w pierwszej macierzy mówią, jak bardzo chcemy karać za wielkość kolejnych zmiennych stanów, a drugi za wielkość sterowania. Zachęcam do zabawy z różnymi wartościami współczynników. Na rysunku 23 pokazano sterowanie uzyskane dla wartości z przykładowego kodu.

Rysunek 23. Położenie belki w funkcji położenia serwomechanizmu

Pierwszy wykres pokazuje wartość zadaną, zmierzone położenie i jego estymatę. Widoczny jest uchyb ustalony. Spowodowany jest on małymi wartościami sterowania, dla których tarcie statyczne nie pozwala kulce ruszyć. Drugi wykres pokazuje wartości wygenerowanego sterowania. Pokazane są tu wartości przed przycięciem do maksymalnej możliwej wartości. Ostatni wykres prezentuje estymatę prędkości oraz położenia serwomechanizmu. Przebiegi dla kilku innych nastaw znajdują się w notatniku jupiter/Experiments.ipynb [13].

Rafał Kozik
rafkozik@gmail.com

Bibliografia: