Jak się przekonamy po lekturze artykułu, zaprojektowanie gotowej aplikacji z zastosowaniem przekaźnika programowalnego Zelio można zrealizować w ciągu jednego wieczoru. Niewykluczone nawet, że jeśli tylko będziemy dysonowali niezbędnymi elementami wykonawczymi (stycznikami, elektrozaworami, przewodami połączeniowymi, gniazdami, elementami mocującymi itp.), możliwe będzie nawet uruchomienie gotowego urządzenia.
Ocenę stopnia skomplikowania projektu pozostawiam czytelnikom. Dla jednych będzie to zapewne zagadnienie banalne, dla innych całkiem złożony problem. Jesteśmy gotowi? Zaczynamy!
Problem
Chociaż aplikacja, którą projektujemy, jest jak najbardziej praktyczna, w tym znaczeniu, że można ją uruchomić w jakimś urządzeniu fizycznym, to jednak sam problem jest zadaniem czysto akademickim. Zadania takie są często rozwiązywane na ćwiczeniach i kolokwiach przez studentów kierunków związanych z automatyką i elektroniką. Możemy więc sprawdzić się i my.
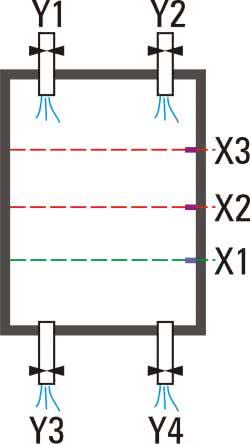
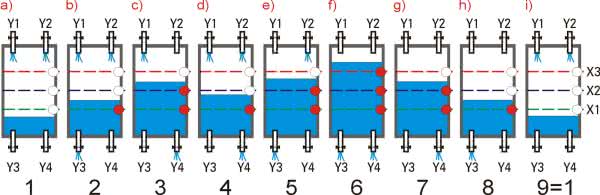
Problem jest następujący. Mamy zbiornik pełniący funkcję mieszalnika jakichś cieczy (rysunek 1). Naszym zadaniem jest opracowanie sterowania czterema elektrozaworami. Dwa z nich (Y1 i Y2) napełniają zbiornik dwoma różnymi cieczami, natomiast pozostałe dwa elektrozawory Y3 i Y4 są wykorzystywane do opróżniania zbiornika. Na trzech różnych wysokościach zainstalowano czujniki poziomu cieczy w zbiorniku. Na podstawie ich wskazań załączane są według przyjętego algorytmu poszczególne elektrozawory. Zasadę działania urządzenia przedstawiono na rysunku 2. Wyróżniono na nim 9 stanów charakterystycznych dla pracy urządzenia. Właściwie jest ich 8, gdyż stan 9 jest powtórzeniem stanu 1. Ważne dla pracy urządzenia są wydajności elektrozaworów. Przyjmijmy, że Y1 ma przepływ 20 l/min, Y2=50 l/min, Y3=-10 l/min, a Y4=-30 l/min. Minus oznacza, że jest to zawór opróżniający zbiornik. Z tych parametrów wynika, że jeśli, na przykład, są włączone elektrozawory: Y1 (napełniający) i Y4 (opróżniający), to wypadkowy przepływ jest równy -10 l/min, a więc zbiornik jest opróżniany.
Przyjmijmy jeszcze na potrzeby projektu, że zawory mają pewną zwłokę działania. Takie założenie uwalania nas od dodatkowych czynności związanych z histerezą, którą należałoby jakoś zaimplementować w projekcie, aby nie dopuścić do stanów niestabilnych przy przejściach przez poszczególne poziomy. W krytycznym przypadku mogłoby to spowodować nawet zawieszenie się programu.
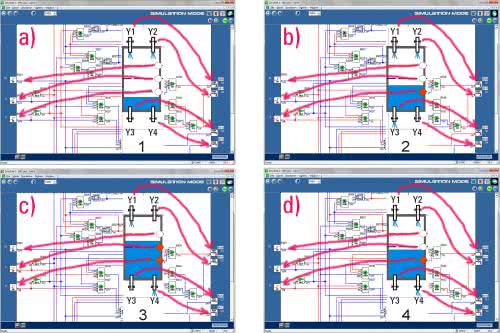
Praca rozpoczyna się od stanu 1, w którym zbiornik jest pusty. Załączone są oba zawory napełniające, tj.: Y1 i Y2 (rysunek 2a).
Po przekroczeniu poziomu X1 nadal pracują zawory napełniające, ale włączony zostaje również zawór opróżniający Y3. Sumaryczny przepływ jest nadal dodatni, więc zbiornik jest napełniany, tylko z nieco mniejszą szybkością (rysunek 2b).
W stanie 3 ciecz przekroczyła poziom X2. Aktywne są czujniki X1 i X2, co powoduje wyłączenie zaworu Y2 i przełączenie zaworów Y3 i Y4. Wypadkowy przepływ jest teraz równy -10 l/min, a więc zbiornik jest opróżniany (rysunek 2c).
Spadek poziomu cieczy poniżej czujnika X2 powoduje załączenie obu zaworów napełniających Y1 i Y2, ale zawór opróżniający Y4 pozostaje załączony. Sumaryczny przepływ jest dodatni, więc zbiornik jest ponownie napełniany (rysunek 2d).
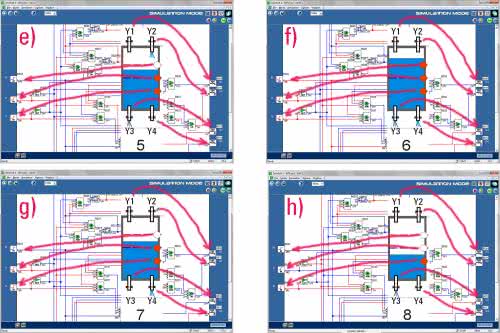
W stanie 5 zostaje przekroczony poziom X2. Tym razem jednak postępowanie jest inne niż w stanie 3. Aktywne są zawory Y2 i Y3 - zbiornik jest napełniany (rysunek 2e).
Przekroczenie poziomu X3 powoduje wyłączenie wszystkich zaworów napełniających i jednoczesne włączenie obu zaworów opróżniających (rysunek 2f). Następuje opróżnianie zbiornika do poziomu minimalnego.
Szybkość opróżniania nie jest jednak stała. Spadek poziomu cieczy poniżej X3 powoduje wyłączenie zaworu Y3. Od tego momentu zbiornik jest opróżniany tylko przez zawór Y4 (rysunek 2g).
Ostatni stan algorytmu ma numer 8. Teraz do czasu przekroczenia poziomu poniżej X1 jest aktywny tylko zawór Y3 (rysunek 2h).
Spadek poziomu cieczy poniżej X1 oznacza zapętlenie się algorytmu. Stan 9 jest równoważny stanowi 1, od którego rozpoczynał się algorytm.
Wszystko wygląda dość skomplikowanie, ale jak się wkrótce przekonamy, implementacja takiego algorytmu nie będzie bardzo trudna.
Implementacja algorytmu
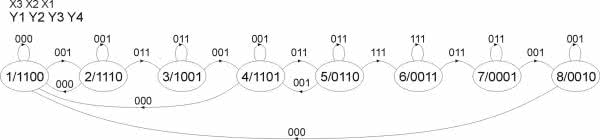
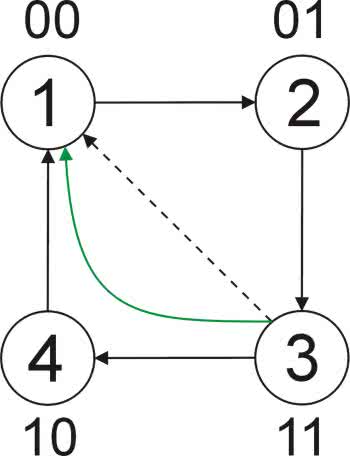
Etap 1. Graf Teraz stoi przed nami zadanie najtrudniejsze. Jak to wszystko zapisać w sposób zrozumiały dla przekaźnika Zelio? W numerze 3/2019 opisano przekaźnik Zelio typu SR3B101BD. Zastosujemy go w naszej aplikacji, używając graficznego środowiska programowania wykorzystującego bloki funkcjonalne (FBO). Tą metodą można implementować algorytmy układów logicznych: kombinacyjnych, co jest oczywiste, ale nawet sekwencyjnych. Z uwagi na wieloznaczność stanów czujników X1, X2 i X3, do realizacji naszego algorytmu konieczne jest zastosowanie jakiegoś automatu. Na szczęście w zasobniku bloków funkcjonalnych przekaźnika Zelio znajdują się m.in. podstawowe funktory logiczne oraz przerzutniki RS, które posłużą do budowy automatu. Zastosujemy więc znaną metodę projektowania układów logicznych i sekwencyjnych wykorzystującą tablice Karnaugh. Zaczynamy od zbudowania grafu określającego reakcje układu na poszczególne wymuszenia. Końcową jego postać przedstawiono na rysunku 3.
W stanie 1 zbiornik jest pusty. Dla wymuszenia 000 (X3 X2 X1) jest to stan stabilny. Automat pozostaje w nim do chwili pojawienia się wymuszenia 001 oznaczającego przekroczenie poziomu X1. W tym stanie aktywne są wyjścia Y1 i Y2 odpowiadające włączeniu obu elektrozaworów napełniających zbiornik. Pod wpływem wymuszenia 001 (inne są niemożliwe) automat przechodzi do stanu 2, w którym zostaje włączony zawór Y3. Naturalnym wymuszeniem jest teraz 011 oznaczające napełnienie zbiornika do poziomu X2, ale może się zdarzyć, że na skutek jakichś zdarzeń (np. awarii innych elementów systemu) ciecze przestaną być podawane. Spowoduje to ponowne obniżenie poziomu cieczy poniżej czujnika X1 (wymuszenie 000). W takim przypadku zawór Y3 powinien być wyłączony. Automat wraca do stanu 1.
Po wystąpieniu wymuszenia 011 w stanie 2 następuje przejście do stanu 3, w którym aktywne są zawory Y1 i Y4. Jak pamiętamy, wypadkowy przepływ jest wówczas ujemny, zbiornik jest więc opróżniany. Pojawia się więc wymuszenie 001, automat nie wraca jednak do stanu 2, lecz przechodzi do stanu 4. Przejście do stanu 2 spowodowałoby zawieszenie się algorytmu. W stanie 4 zbiornik jest napełniany przez oba zawory Y1 i Y2, mimo że otwarty jest zawór opróżniający Y4. Przewidziano jednak awaryjny powrót do stanu 1, który nastąpi w przypadku zaprzestania podawania cieczy.
Automat przechodzi do stanu 5, jeśli zostanie przekroczony poziom X2 (wymuszenie 011 w stanie 4) i pozostaje w nim do chwili przekroczenia poziomu X3 (wymuszenie 111). I w tym przypadku przewidziano reakcję na awarię systemu powodująceą zaprzestanie podawania cieczy. W stanie 5 pojawi się wówczas wymuszenie 001, a w jego wyniku przejście do stanu 4. W czasie normalnej pracy oczekiwane jest jednak wymuszenie 111 oznaczające przekroczenie poziomu X3. Powoduje ono przejście automatu do stanu 6, w którym zostają wyłączone oba zawory napełniające przy jednoczesnym włączeniu obu zaworów opróżniających. W stanach 7 i 8 kontynuowane jest opróżnianie zbiornika, przy czym przekroczenie poziomu X2 (wymuszenie 001 w stanie 7) powoduje przełączenie zaworów Y4 na Y3. Zanik sygnału z czujnika X1 oznacza obniżenie poziomu cieczy do poziomu początkowego, automat przechodzi więc ponownie do stanu 1 i cały cykl się powtarza.
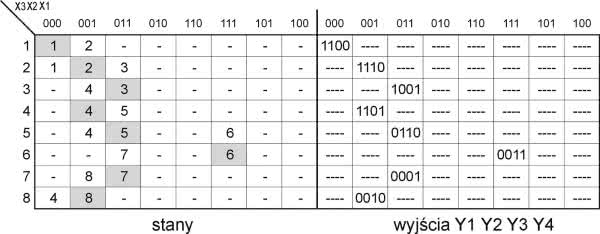
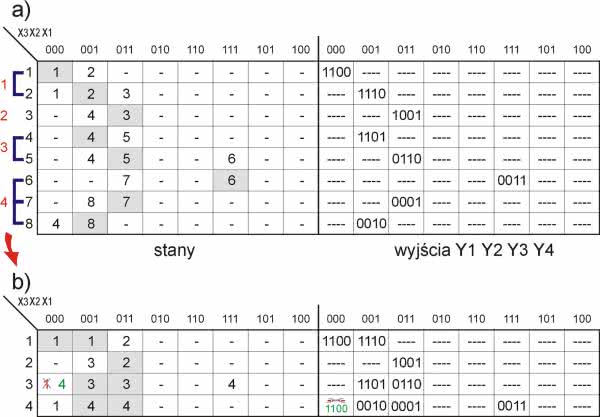
Etap 2. Tablica przejść-wyjść Kolejnym etapem projektowania jest zapisanie grafu w postaci tabelarycznej umożliwiającej podjęcie kolejnych kroków prowadzących do narysowania schematu układu logicznego naszego sterownika. Tabelę taką przedstawiono na rysunku 4. Tabela składa się z dwóch części. W lewej zawarto przejścia pomiędzy poszczególnymi stanami pod wpływem wymuszeń zapisanych w kolejnych kolumnach tabeli. Wiersze reprezentują stany automatu. Pola pokolorowane oznaczają, że dla danego wymuszenia podanego w opisie kolumny jest to stan stabilny. Tylko dla takich stanów stabilnych określone są wyjścia automatu podane w prawej części tabeli. W polach niepokolorowanych zawarto stany, do których powinien przejść automat pod wpływem określonych wymuszeń. Kreski w polach tabeli oznaczają, że może w nich wystąpić dowolna wartość. To są nasze ulubione pola, gdyż można w nie wpisywać wartości, które będą nam najlepiej odpowiadać na etapie minimalizacji.
Minimalizacja to ważny etap naszego projektu. Dzięki temu zabiegowi znacznie uprościmy połączenia końcowego układu logicznego, jednocześnie zmniejszając do minimum liczbę użytych funktorów i przerzutników. Minimalizacja polega na znalezieniu stanów niesprzecznych i sklejeniu ich ze sobą. Najważniejszym zagadnieniem minimalizacji jest więc wyszukanie takich stanów, które nie powodują konfliktu na wyjściach i jednocześnie zachowują logikę przejść pomiędzy stanami.
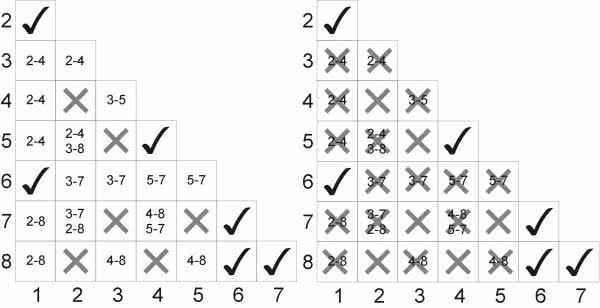
Przeanalizujmy na przykład stany 1 i 2. Jak widać, dla wymuszeń 000 i 001 w tabeli występują te same stany, do których automat powinien przejść pod ich wpływem. W stanie 1 dla wymuszenia 011 występują kreski, a w stanie 2 dla tego wymuszenia jest wpisany stan 3. Jak już wspomniano, w miejsce kresek można wpisać dowolną wartość, jeśli więc dla stanu 1 wpisalibyśmy 3 dla wymuszenia 011, to uzyskalibyśmy jeden nowy stan zamiast dwóch. Najważniejsze jest jednak sprawdzenie, czy nie wystąpi konflikt na wyjściu. Sprawdzamy więc wyjścia dla stanów 1 i 2 w prawej części tabeli i okazuje się, że wprawdzie mamy różne stany wyjściowe, ale występują one dla różnych wymuszeń. Bez przeszkód można więc skleić stany 1 i 2 w jeden nowy. Takich przypadków może być jednak więcej. Należy więc sprawdzić wszystkie kombinacje, tzn. każdy stan z każdym. Wyniki tej operacji zapisujemy w diagramie przedstawionym na rysunku 5. Dla każdego przypadku postępujemy tak, jak to opisano wyżej. Jeśli rozpatrywane stany są niesprzeczne, np. 1 i 2, w polu na przecięciu opisów 1 i 2 umieszczamy ptaszek. Jeśli rozpatrywana para stanów jest sprzeczna (występuje konflikt wyjść), w danym polu umieszczamy krzyżyk. Może się jednak zdarzyć, że dla rozpatrywanej pary stanów nie ma konfliktu na wyjściach, ale nie ma też identycznych przejść między stanami. Jest tak na przykład dla pary 1 i 3 naszego automatu. O ile wyjścia można bez problemu skleić ze sobą, o tyle dla wymuszenia 001 w stanie 1 automat przechodzi do stanu 2, natomiast dla tego samego wymuszenia w stanie 3 powinno nastąpić przejście do stanu 4. Ponieważ na razie nie wiemy, czy stany 2 i 4 są niesprzeczne, w polu diagramu na przecięciu opisów 1 i 3 należy wpisać parę podejrzaną 2-4. To, czy będzie możliwe sklejenie stanów 1 i 3, okaże się później, w trakcie dalszej analizy. Podobnie postępujemy dla każdej kolejnej pary, tak aby wypełnić cały diagram. Po wykonaniu wszystkich powyższych czynności powinien on wyglądać tak, jak na rysunku 5a. Teraz sprawdzamy, czy dla wszystkich warunkowych przejść nie występują stany sprzeczne. Jeśli tak, w danym polu wstawiamy krzyżyk. Na przykład dla stanów 1 i 3 występuje warunkowe przejście 2-4. Po sprawdzeniu okazuje się jednak, że stany 2 i 4 są sprzeczne, więc stany 1 i 3 również będą sprzeczne - w pozycji 1-3 umieszczamy krzyżyk. I znowu rozpatrujemy wszystkie przypadki, a ostatecznie diagram przybiera postać jak na rysunku 5b.
Z diagramu wynika, że można skleić stany 1 i 2. W kolumnie 1 jest też para niesprzeczna 1-6, ale stanu 6 nie można dokleić do pary 1-2, gdyż stan 2 jest sprzeczny ze stanem 6. Dalsza analiza prowadzi do wniosku, że można ze sobą skleić stany 1-2, 4-5 oraz 6-7-8. Udało się więc zredukować liczbę stanów o połowę. Po wykonaniu tej operacji możemy zmodyfikować tabelę przejść tak, jak to przedstawiono na rysunku 6. W wynikowej tabeli uwzględniono nową numerację stanów. Jest to tablica minimalna.
Kodowanie stanów
Kolejnym etapem projektowania jest kodowanie stanów, czyli nadanie im wartości binarnych. Kody stanów odpowiadają stanom przekaźników wykorzystywanych do realizacji automatu. Tablica minimalna zawiera 4 stany, automat będzie więc zbudowany na dwóch przekaźnikach. Bardzo ważnym zagadnieniem jest taka realizacja projektu, aby przy przejściach ze stanu do stanu nie następowała jednoczesna zmiana wyjść przerzutników. W praktyce zawsze jeden z nich będzie szybszy, a to może powodować skoki do stanów niezgodnych z tablicą przejść. Sprawdźmy więc, jaka jest sekwencja przejść w naszym automacie. Przedstawiono ją na rysunku 7. Jak widać, występuje niekorzystne przejście ze stanu 3 do 1, w którym kody stanów zmieniają się jednocześnie na obu pozycjach. Zauważamy jednak, że dla tego samego wymuszenia (000) następuje przejście ze stanu 4 do 1. Wykorzystujemy ten fakt i w tablicy przejść w wierszu 3 jedynkę zastępujemy cyfrą 4. Oznacza to, że w stanie 3 dla wymuszenia 000 nastąpi przejście do stanu 4, ale dla tego wymuszenia nie jest to stan stabilny, więc natychmiast zostanie wykonany skok do stanu 1. Automat pozostanie w nim, gdyż jest to stan stabilny.
Jest jeszcze jedno zagadnienie, które należy rozpatrzyć w związku z zaistniałą sytuacją. W tablicy wyjść w stanach 3 i 4 dla wymuszenia 000 występują kreski, które jak wiemy oznaczają wartość dowolną, w tym przypadku nieokreśloną. Rozważmy więc przypadek, w którym w stanie 3 na wyjściu np. Y4 wystąpi poziom niski, a w stanie 4 wysoki. W stanie docelowym (1) ponownie występuje poziom niski. Podczas przerzutu 3-4-1 mógłby więc wystąpić krótkotrwały niepożądany impuls 0-1-0. Teoretycznie mógłby on zakłócić pracę urządzenia. W projektowanej aplikacji impuls taki raczej nie powinien powodować niepożądanych skutków, gdyż czas przejścia ze stanu 3 przez 4 do 1 jest pomijalnie krótki w odniesieniu do bezwładności elektrozaworu. Projekt wykonamy jednak zgodnie ze sztuką. Metodą uniknięcia szpilki podczas przejść przez dwa stany jest ustawienie wyjść w stanie przejściowym (4) takich, jakie występują na końcu przejścia. Kreski w kolumnie 000 dla stanu 4 zastępujemy więc zapisem 1100, który odpowiada poziomom wyjściowym w stanie 1 pod wpływem wymuszenia 000.
Zakodowana tablica przejść automatu
Kodowanie stanów przyjmujemy zgodnie z rysunkiem 7. Mamy więc: stan 1 - kod 00, stan 2 - kod 01, stan 3 - kod 11 i stan 4 - kod 10. Zauważmy, że stany są kodowane kodem Graya gwarantującym zmiany tylko na jednej pozycji w sąsiadujących stanach.
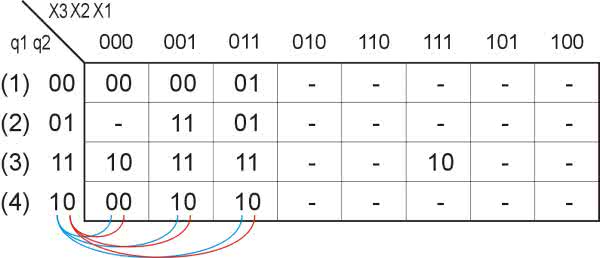
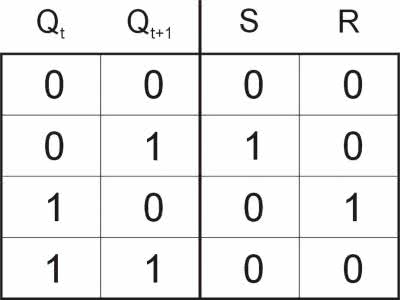
Zakodowaną tablicę stanów przedstawiono na rysunku 8. Posłuży ona do utworzenia tablicy wymuszeń dla przerzutników tworzących automat. W zasobniku bloków funkcjonalnych środowiska graficznego opracowanego dla przekaźnika programowalnego Zelio umieszczono przerzutniki RS. Wykorzystamy je do budowy automatu. Przerzutniki te mają dwa wejścia: S (Set) i R (Reset). Podanie poziomu wysokiego na wejście S powoduje ustawienie wyjścia w stanie wysokim, analogicznie poziom wysoki na wejściu R powoduje wyzerowanie wyjścia przerzutnika. Jak nietrudno zauważyć, należy unikać jednoczesnego podawania stanów wysokich na wejścia R i S, gdyż powoduje to nieokreśloną reakcję, natomiast stany niskie na obu wejściach nie wywołują żadnych zmian na wyjściach przerzutników. Tablicę stanów przerzutnika RS przedstawiono na rysunku 9.
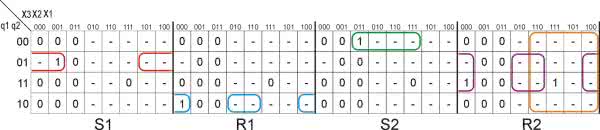
Kolumna Qt zawiera stany przed ich zmianą, kolumna Qt+1 po zmianie. Kombinacje Qt=0 i Qt+1=0 oraz Qt=1 i Qt+1=1 odpowiadają sytuacji, w której wyjścia nie ulegają zmianie, zatem na wejściach R i S powinny być utrzymywane stany niskie. Możemy już przystąpić do utworzenia tablicy przejść dla naszego automatu. Składa się ona z 4 segmentów zawierających stany, na podstawie których utworzymy funkcje wzbudzeń dla wejść R1, S1 (przerzutnik Q1 automatu) i R2, S2 (przerzutnik Q2 automatu). Wypełniamy ją na podstawie zakodowanej tablicy przejść automatu (rysunek 8) oraz tablicy przejść przerzutnika RS (rysunek 9). Metodę postępowania zilustrowano na przykładzie stanu 4 w tablicy z rysunku 8. Przejścia dla przerzutnika Q1 zaznaczono niebieskimi połączeniami, a dla przerzutnika Q2 czerwonymi. Przykładowo: w stanie 4 (10) wyjście przerzutnika Q1 jest w stanie 1, a na skutek wymuszenia 000 powinno przejść do stanu 0. Patrzymy, jaka kombinacja wejść przerzutnika RS odpowiada przypadkowi Qt=1 i Qt+1=0. Okazuje się, że jest to: S=0, R=1. Takie wartości wpisujemy więc w kolumnie 000 tablicy przejść automatu w sekcjach S1 i R1 w wierszu odpowiadającym stanowi 11. Analogicznie, dla tego samego wymuszenia wyjście przerzutnika Q2 nie ulega zmianie, więc pola S2 i R2 przyjmują wartości 0. Podobnie wypełniamy całą tabelę, a końcowy wynik tej operacji przedstawiono na rysunku 10. Do tej tablicy wrócimy, gdy będziemy formułować funkcje wzbudzeń, wcześniej jednak zajmiemy się jeszcze tablicą wyjść.
Zakodowana tablica wyjść
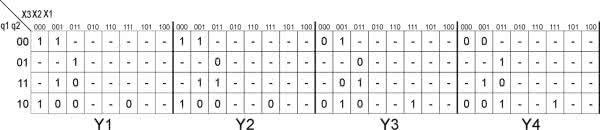
Tablicę wyjść tworzy się w sposób analogiczny. Tym razem działania są jednak znacznie prostsze, gdyż nie trzeba uwzględniać żadnych przerzutników. Rozpatrujemy jedynie wyjścia Y1...Y4. Ta operacja polega w zasadzie na rozdzieleniu wyjść z tablicy przedstawionej na rysunku 6. Otrzymujemy więc tablicę taką, jak na rysunku 11. Przed nami pozostała już tylko najbardziej fascynująca operacja, jaką jest definiowanie funkcji wzbudzeń oraz funkcji wyjściowych automatu.
Definiowanie funkcji wzbudzeń przerzutników
Wracamy do tablicy przejść, aby zdefiniować funkcje wzbudzeń. W wyniku otrzymamy funkcje logiczne definiujące stany, jakie powinny być podawane na wejścia R i S przerzutników, tak aby nasz automat przechodził od stanu do stanu zgodnie z grafem zbudowanym w pierwszej fazie projektu. Funkcje te zrealizujemy za pomocą typowych funktorów logicznych, tj. bramek AND, NAND, OR, NOR, XOR i NOT.
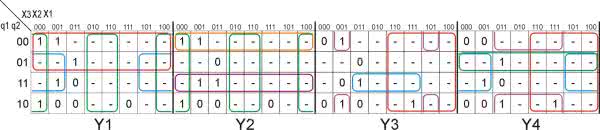
Zasadę postępowania opisano niżej. W każdej tablicy przejść, tj. niezależnie dla wejścia S1, R1, S2 i R2, zakreślamy pola zawierające jedynki. Czynność ta powinna być wykonana tak, aby każdy zakreślony obszar obejmował 2n pól, a ponadto pola te powinny być położone symetrycznie względem osi symetrii tablicy. W zakreślanym polu mogą znaleźć się same jedynki i kreski. Zakreślonych pól może być kilka tak, aby nie pominąć żadnej jedynki. Tablicę traktujemy tak, jakby nie miała ograniczających krawędzi. Oznacza to, że można ze sobą sklejać pola znajdujące się przy krawędziach, mimo że są oddzielone polami zawierającymi zera. Należy dążyć do zakreślania jak największych obszarów. Dzięki temu uzyskuje się największe uproszczenie funkcji.
Zaczynamy na przykład od funkcji wzbudzeń dla wejścia S1. W tym przypadku wystarczy zakreślić jedno pole zaznaczone kolorem czerwonym na rysunku 12. Jest ono wprawdzie rozdzielone, ale zgodnie z wcześniejszą uwagą może być traktowane jak jedno. To pole określa jednoznacznie kombinację wszystkich sygnałów definiujących wzbudzenie dla wejścia S1. Odpowiada ona stanom: q1, q2 i X2. Sygnały X1 i X2 pomijamy, gdyż zmieniają się one w zasięgu zakreślonego pola, są więc od nich niezależne. Ostatecznie funkcja wzbudzeń dla wejścia S1 jest następująca:
S1=q1*q2*X2
gdzie * oznacza iloczyn logiczny (AND)
Analogicznie postępujemy dla wejścia R1. Można dla niego zakreślić pola z kreskami leżące na pionowej osi symetrii tablicy. Zakreślone pole definiuje funkcję wzbudzeń dla wejścia R1. Ma ona ostatecznie postać:
R1= q1*q2*X1
Zakreślone pole dla wejścia S2 następnego przerzutnika definiuje funkcję wzbudzeń:
S2=q1*q2*X2
Nieco bardziej skomplikowana będzie funkcja wzbudzeń dla wejścia R2. Jak widać, mamy tu dwa pola. Jedno zaznaczone kolorem pomarańczowym, drugie fioletowym. Funkcja wzbudzeń będzie się więc składała z dwóch elementów:
R2=q2*X1+X3
Znak „+” w powyższej formule oznacza logiczną sumę (OR). Już jesteśmy prawie gotowi do narysowania schematu. Pozostaje jeszcze zdefiniowanie funkcji wyjść.
Definiowanie funkcji wyjść
Do określenia funkcji wyjść korzystamy z tablicy wyjść z rysunku 11. Postępujemy analogicznie jak wcześniej. Tablicę z zakreślonymi polami przedstawiono na rysunku 13. Na tej podstawie określamy funkcje wyjść:
Y1=q1+X1+q2*X2
Y2=X1+q1*q2+q1*q2
Y3=X3+q1*q2*X2+q2*X2*X1
Y4= X3+q1*q2+q2*X2+q2*X2
Mamy już wszystkie dane do narysowania schematu w środowisku Zelio Soft2.
Sporządzenie schematu w środowisku Zelio Soft2
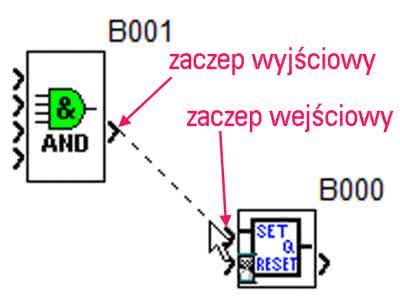
Aplikację z przekaźnikiem programowalnym Zelio SR3 przygotowujemy w środowisku Zelio Soft2. Wybieramy polecenie tworzenia nowego programu i w kolejnych oknach wskazujemy przekaźnik SR3B101BD. Ważne jest, aby w oknie wyboru typu programowania wybrać opcję FBD, nie Ladder. Uzyskamy tym samym dostęp do bloków funkcjonalnych, z których zbudujemy urządzenie. Każdy funktor ma zaczepy na wejściach i wyjściach służące do wykonywania połączeń. Połączenie jest inicjowane po najechaniu kursorem na zaczep początkowy, np. wyjściowy, i naciśnięciu lewego przycisku myszki. Następnie nie zwalniając przycisku, umieszczamy kursor w punkcie docelowym, np. na jakimś zaczepie wejściowym, i zwalniamy przycisk (rysunek 14).
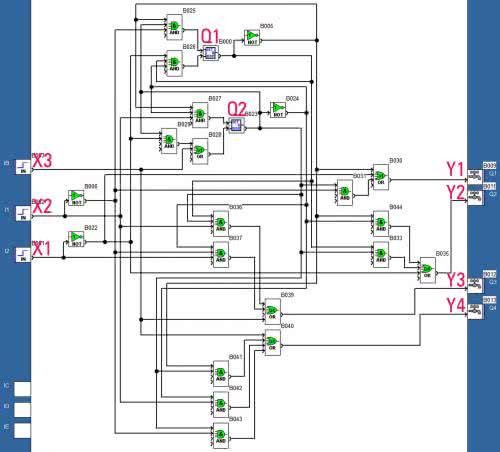
Teraz przed nami dość mozolna praca polegająca na wprowadzeniu do obszaru roboczego odpowiednich funktorów z zasobnika znajdującego się u dołu ekranu, a następnie dokonaniu wszystkich niezbędnych połączeń. Schemat ideowy naszego sterownika jest dość złożony, więc etap jego wprowadzenia zajmie nam pewien czas. Ostatecznie powinniśmy uzyskać połączenia mniej więcej takie, jak na rysunku 15.
Właściwie wszystko mamy zrobione. Teraz już tylko to, co konstruktorzy lubią najbardziej, czyli pierwsze włączenie układu. My zrobimy to wirtualnie, bez obaw, że coś spłonie. Wykorzystamy do tego wbudowany w środowisko Zelio Soft2 symulator.
Symulowanie pracy układu
Symulator jest uruchamiany np. przyciskiem ekranowym z literką „S” znajdującym się w prawym-górnym rogu ekranu. Po jego naciśnięciu środowisko Zelio Soft2 przechodzi w tryb symulacji, ale nasz program nie zostaje automatycznie uruchomiony. Konieczne jest jeszcze naciśnięcie przycisku Run. Teraz już żarty się kończą, widzimy, że oba kraniki napełniające są otwarte i do naszego wirtualnego zbiornika nalewane są płyny. Stany poszczególnych linii sygnałowych naszego układu są sygnalizowane kolorami. Kolor niebieski oznacza stan niski (0), kolor czerwony oznacza stan wysoki (1). Widzimy, że wszystkie czujniki znajdujące się na lewej krawędzi ekranu są wyłączone. Prześledźmy teraz zachowanie się sterownika pod wpływem symulowanych wymuszeń, konfrontując poszczególne stany z założonym algorytmem. Symulację taką przedstawiono na kolejnych rysunkach 16a...h. Aby włączyć wirtualny czujnik (X1, X2 lub X3), należy najechać na niego myszką i przycisnąć lewy przycisk. Czujnik zmieni stan. Sekwencję wymuszeń wykonujemy ręcznie, a dla każdego z nich sprawdzamy stany wirtualnych elektrozaworów. Jak widać, automat porusza się zgodnie z projektem, a elektrozawory są włączane zgodnie z założeniami. Możemy więc niczym fotografowie branży modelingowej krzyknąć „Mamy to!”.
Jarosław Doliński, EP

 Zaloguj
Zaloguj